No CrossRef data available.
Published online by Cambridge University Press: 13 September 2024
We study the asymptotic behaviour of the least energy solutions to the following class of nonlocal Neumann problems: 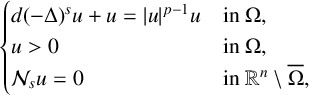 $$ \begin{align*} \begin{cases} { d(-\Delta)^{s}u+ u= \vert u\vert^{p-1}u } & \text{in } \Omega, \\ {u>0} & \text{in } \Omega, \\ { \mathcal{N}_{s}u=0 } & \text{in } \mathbb{R}^{n}\setminus \overline{\Omega}, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} { d(-\Delta)^{s}u+ u= \vert u\vert^{p-1}u } & \text{in } \Omega, \\ {u>0} & \text{in } \Omega, \\ { \mathcal{N}_{s}u=0 } & \text{in } \mathbb{R}^{n}\setminus \overline{\Omega}, \end{cases} \end{align*} $$
where 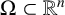 $\Omega \subset \mathbb {R}^{n}$ is a bounded domain of class
$\Omega \subset \mathbb {R}^{n}$ is a bounded domain of class 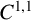 $C^{1,1}$,
$C^{1,1}$, 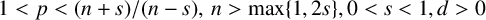 $1<p<({n+s})/({n-s}),\,n>\max \{1, 2s \}, 0<s<1, d>0$ and
$1<p<({n+s})/({n-s}),\,n>\max \{1, 2s \}, 0<s<1, d>0$ and 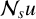 $\mathcal {N}_{s}u$ is the nonlocal Neumann derivative. We show that for small
$\mathcal {N}_{s}u$ is the nonlocal Neumann derivative. We show that for small 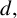 $d,$ the least energy solutions
$d,$ the least energy solutions 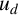 $u_d$ of the above problem achieve an
$u_d$ of the above problem achieve an 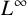 $L^{\infty }$-bound independent of
$L^{\infty }$-bound independent of 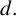 $d.$ Using this together with suitable
$d.$ Using this together with suitable 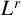 $L^{r}$-estimates on
$L^{r}$-estimates on 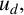 $u_d,$ we show that the least energy solution
$u_d,$ we show that the least energy solution 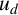 $u_d$ achieves a maximum on the boundary of
$u_d$ achieves a maximum on the boundary of  $\Omega $ for d sufficiently small.
$\Omega $ for d sufficiently small.
Communicated by Florica C. Cîrstea