Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T14:15:53.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Admissible solutions of the Schwarzian differential equation

Part of: Qualitative theory Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  09 April 2009

Katsuya Ishizaki
Katsuya Ishizaki
Affiliation:
Department of Mathematics Tokyo National College of Technology1220 -2 Kunugida-cho Hachioji Tokyo 193, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R(z, w) be a rational function of w with meromorphic coefficients. It is shown that if the Schwarzian equation possesses an admissible solution, then 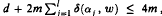, where αj, are distinct complex constants. In particular, when R(z, w) is independent of z, it is shown that if (*) possesses an admissible solution w(z), then by some Möbius transformation u = (aw + b) / (cw + d) (ad – bc ≠ 0), the equation can be reduced to one of the following forms: 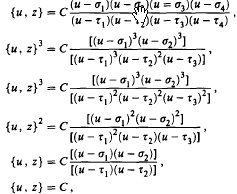where τj (j = 1, … 4) are distinct constants, and σj (j = 1, … 4) are constants, not necessarily distinct.

Keywords

admissible solutionSchwarzianNevanlinna theory

MSC classification

Secondary: 34C10: Oscillation theory, zeros, disconjugacy and comparison theory 30D35: Distribution of values, Nevanlinna theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 50 , Issue 2 , April 1991 , pp. 258 - 278
Copyright
Copyright © Australian Mathematical Society 1991

References

[1]Hayman, W. K., Meromorphic functions, (Oxford University Press, 1964).Google Scholar
[2]Hille, E., Ordinary differential equations in the complex domain, (Wiley-Interscience, New York, 1976).Google Scholar
[3]Ishizaki, K., ‘On some generalizations of theorems of Toda and Weissesnborn to differential polynomials’, Nagoya Math. J. 115 (1989), 199–207.CrossRefGoogle Scholar
[4]Ishizaki, K., ‘Deficiencies of the admissible solutions of the Schwarzian differential equations and the Ricatti equations’, Res. Rep. Tokyo Nat. College Tech. 20 1988.Google Scholar
[5]Jank, G. and Volkmann, L., Meromorphe Funktionen und Differential-geichungen, (Birkhäuser-Verlag, Basel, Boston, Stuttgart, 1985).Google Scholar
[6]Laine, I., ‘On the behaviour of the solutions of some first order differential equations’, Ann. Acad. Sci. Fenn. Ser. A I, 497 (1971), 1–26.Google Scholar
[7]Mokhon'sko, A. Z., ‘On the Nevanlinna characteristics of certain meromorphic functions’, (Russian). Teor. Funkcil Funkcional. Anal. i Priložen. 14 (1971), 83–87.Google Scholar
[8]Mues, E., ‘Uber faktorisierbare Lösungen von Riccatischen Differentialgeichungen’, Math. Z. 121 (1971), 145–156.CrossRefGoogle Scholar
[9]Nevanlinna, R., Analytic functions, (Springer-Verlag, Berlin, Heidelberg, New York, 1970).CrossRefGoogle Scholar
[10]Rieth, J. V., Untersuchungen Gewisser Klassen Gewöhnlicher Differentialgleichungen erster und zweiter ordnung im Komplexen, (Doctoral Dissertation, Technische Hochschule, Aachen, 1986).Google Scholar
[11]Steinmetz, N., ‘On factorization of the solutions of the Schwarzian differential equation {w, z} = q(z)’, Funkcial Ekvac. 24 (1981), 307–315.Google Scholar
[12]Yuzan, He and Laine, I., ‘The Hayman-Miles theorem and the differential equation (y1)n = R(z, y)’, to appear.Google Scholar