Article contents
ON WARING’S PROBLEM IN SUMS OF THREE CUBES FOR SMALLER POWERS
Published online by Cambridge University Press: 16 September 2021
Abstract
We give an upper bound for the minimum s with the property that every sufficiently large integer can be represented as the sum of s positive kth powers of integers, each of which is represented as the sum of three positive cubes for the cases
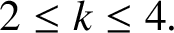 $2\leq k\leq 4.$
$2\leq k\leq 4.$
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by D. Badziahin
The author’s work was supported in part by a European Research Council Advanced Grant under the European Union’s Horizon 2020 research and innovation programme via grant agreement no. 695223 during his studies at the University of Bristol.
References
- 1
- Cited by



