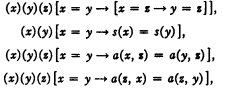Errata
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. iv
-
- Article
-
- You have access
- Export citation
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. iv
-
- Article
-
- You have access
- Export citation
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. iv
-
- Article
-
- You have access
- Export citation
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. iv
-
- Article
-
- You have access
- Export citation
Research Article
Emch's calculus and strict implication
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 77-86
-
- Article
- Export citation
Set-theoretic foundations for logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 45-57
-
- Article
- Export citation
Other
A statement of policy
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 1
-
- Article
- Export citation
A Bibliography of Symbolic Logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 121-216
-
- Article
- Export citation
Research Article
Extensions of some theorems of Gödel and Church
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 87-91
-
- Article
- Export citation
Other
Index of Authors
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 217-218
-
- Article
- Export citation
Research Article
Toward a calculus of concepts
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 2-25
-
- Article
- Export citation
Other
Addendum to the article Implication and deducibility
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 58
-
- Article
- Export citation
Research Article
A system of formal logic without an analogue to the curry W operator1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 92-100
-
- Article
- Export citation
Other
Issue and Subscriber Information
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 219
-
- Article
- Export citation
Research Article
Implication and deducibility
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 26-35
-
- Article
- Export citation
Other
Abstracts of papers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 59-62
-
- Article
- Export citation
Front matter
JSL volume 1 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Reviews
Gr. C. Moisil. Recherches sur l'algèbre de la logique. Annales scientifiques de l'Université de Jassy, vol. 22 (1936), pp. 1–118.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 63
-
- Article
- Export citation
Research Article
Constructibility as a criterion for existence
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 36-39
-
- Article
- Export citation
Correction to A note on the Entscheidungsproblem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 101-102
-
- Article
- Export citation

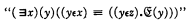
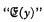 is understood as any statement about
is understood as any statement about