Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T00:35:18.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Correction to A note on the Entscheidungsproblem

Published online by Cambridge University Press:  12 March 2014

Alonzo Church
Alonzo Church*
Affiliation:
Princeton University
Get access Rights & Permissions [Opens in a new window]

Extract

In A note on the Entscheidungsproblem the author gave a proof of the unsolvability of the general case of the Entscheidungsproblem of the engere Funktionenkalkül. This proof, however, contains an error, in order to correct which it is necessary to modify the “additional axioms” of the system L so that they contain no free variables (either free individual variables or free propositional function variables).

The additional axioms of L other than x=y→[F(x)→F(y)] contain no free propositional function variables, and hence it is sufficient to replace each one by an expression obtained from it by quantifying all the individual variables by means of universal quantifiers initially placed—thus, in particular, x = x is replaced by (x)[x=x]. Moreover the axiom x=y→[F(x)→F(y)] may be replaced by the following set of axioms:

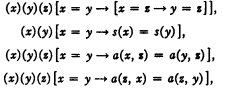
and similar axioms for each of the functions b1, b2, …, bk.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 1 , Issue 3 , September 1936 , pp. 101 - 102
Copyright
Copyright © Association for Symbolic Logic 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 The journal of symbolic logic, vol. 1 (1936), pp. 40–41Google Scholar.

2 The author is indebted to Paul Bernays for pointing out this error and suggesting the method of correcting it, as also for calling attention to the desirability of distinguishing in this connection (as is done below) between proofs which are constructive (finite) and those which are not.

3 When a formula containing free variables is asserted, these free variables may be thought of as having been bound by suppressed universal quantifiers. And on combining several such formulas (or negating such a formula) it may be necessary to restore the suppressed quantifiers in order to avoid confusions of scope. Thus, if U contains free variables, the proposition meant when U→R is asserted is not an implication between the proposition meant when U is asserted and that meant when R is asserted (this observation, and the consequent technique of restoring suppressed quantifiers in such cases, are, of course, a familiar matter to users of the functional calculus). It is in this, or, more strictly, in formal matters which parallel it, that the error lies in the present instance.

4 In the presence of the axioms and rules of the engere Funktionenkalkül, these axioms suffice for the derivation of any expression which may be obtained from x=y→ [F(x)→F(y)] by replacing F by a propositional function, which is expressible in the notation of L, and which does not involve free propositional function variables. Cf. Hilbert, and Bernays, , Grundlagen der Mathematik, vol. 1 (Berlin 1934), pp. 373–375Google Scholar.

5 Bernays's proof is adequate to establish the property constructively in this positive form. See the mimeographed notes of his lectures at The Institute for Advanced Study, p. 122.

6 Similarly the condition of ω-consistency, on the last page of An unsolvable problem of elementary number theory (American journal of mathematics, vol. 58 (1936), pp. 345–363)Google Scholar, should be replaced by the condition: Where E is the existential quantifier over the class of positive integers, if (Ex)P is provable then of some one of the formulas P1, P2, P3, … it is true that the negation is not provable. This condition we may call strong ω-consistency.