Research Article
Classifying positive equivalence relations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 529-538
-
- Article
- Export citation
On the number of countable homogeneous models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 539-541
-
- Article
- Export citation
On the expressibility hierarchy of Magidor-Malitz quantifiers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 542-557
-
- Article
- Export citation
On the interpretation of combinators with weak reduction1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 558-563
-
- Article
- Export citation
A note on the undefinability of cuts
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 564-569
-
- Article
- Export citation
Some model theory of modules. I. On total transcendence of modules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 570-574
-
- Article
- Export citation
Mapping a set of reals onto the reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 575-584
-
- Article
- Export citation
A selection theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 585-594
-
- Article
- Export citation
A second paper “On the interpolation theorem for the logic of constant domains”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 595-599
-
- Article
- Export citation
Sets constructed from sequences of measures: Revisited
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 600-609
-
- Article
- Export citation
Degrees of recursively enumerable topological spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 610-622
-
- Article
- Export citation
Additive structure in uncountable models for a fixed completion of P
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 623-628
-
- Article
- Export citation
Some recent developments in higher recursion theory1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 629-642
-
- Article
- Export citation
Forcing closed unbounded sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 643-657
-
- Article
- Export citation
On forcing without the continuum hypothesis1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 658-661
-
- Article
- Export citation
Definability of r. e. sets in a class of recursion theoretic structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 662-669
-
- Article
- Export citation
Forcing in intuitionistic systems without power-set1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 670-682
-
- Article
- Export citation
Some local definability results on countable topological structures1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 683-692
-
- Article
- Export citation
Orbits of hyperhypersimple sets and the lattice of Σ03 sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 693-699
-
- Article
- Export citation
The τ-theory for free groups is undecidable
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 700-703
-
- Article
- Export citation

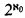 such models. He conjectures that if a countable theory
such models. He conjectures that if a countable theory 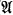 ,
, 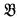 .
. 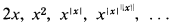 we can define J ⊆
we can define J ⊆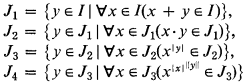
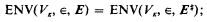
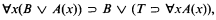
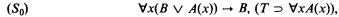
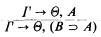
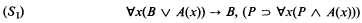
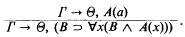
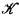 any r.e. open subset of
any r.e. open subset of 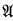 is a recursively saturated model of Pr = Th(
is a recursively saturated model of Pr = Th(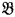 such that
such that 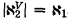 , and because
, and because 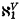 remains a cardinal and, in fact, no new countable sets are added. But to prove that
remains a cardinal and, in fact, no new countable sets are added. But to prove that 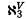 remains a cardinal we need
remains a cardinal we need 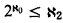 to conclude ∣
to conclude ∣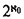 is actually collapsed in
is actually collapsed in 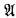 an
an 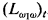 .
. 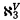 closed under negation (⇁), countable disjunction (∨), countable conjunction (∧), quantification over individual variables (∃
closed under negation (⇁), countable disjunction (∨), countable conjunction (∧), quantification over individual variables (∃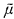 denotes the least system of subsets of
denotes the least system of subsets of 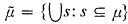 .
.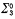 and
and