The number of homogeneous models has been studied in [1] and other papers. But the number of countable homogeneous models of a countable theory T is not determined when dropping the GCH. Morley in [2] proves that if a countable theory T has more than ℵ1 nonisomorphic countable models, then it has 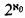such models. He conjectures that if a countable theory T has more than ℵ0 nonisomorphic countable models, then it has 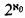such models. In this paper we show that if a countable theory T has more than ℵ0 nonisomorphic countable homogeneous models, then it has 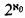such models.

We adopt the conventions in [1]–[3]. Throughout the paper T is a theory and the language of T is denoted by L which is countable.

Lemma 1. If a theory T has more than ℵ0types, then T has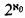nonisomorphic countable homogeneous models.

Proof. Suppose that T has more than ℵ0 types. From [2, Corollary 2.4] T has 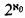types. Let σ be a Ttype with n variables, and T′ = T ⋃ {σ(c1, …, cn)}, where c1, …, cn are new constants. T′ is consistent and has a countable model (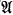, a1, …, an). From [3, Theorem 3.2.8] the reduced model 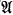has a countable homogeneous elementary extension 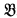. σ is realized in 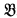. This shows that every type σ is realized in at least one countable homogeneous model of T. But each countable model can realize at most ℵ0 types. Hence T has at least 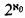countable homogeneous models. On the other hand, a countable theory can have at most 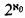nonisomorphic countable models. Hence the number of nonisomorphic countable homogeneous models of T is .

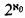In the following, we shall use the languages Lα (α = 0, 1, 2) defined in [2]. We give a brief description of them. For a countable theory T, let K be the class of all models of T. L = L0 is countable.