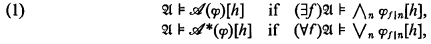Errata
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. v
-
- Article
-
- You have access
- Export citation
Research Article
On degrees of unsolvability and complexity properties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 529-540
-
- Article
- Export citation
Canonical Partition Relations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 541-554
-
- Article
- Export citation
“Helping”: several formalizations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 555-566
-
- Article
- Export citation
The foundations of Suslin logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 567-575
-
- Article
- Export citation
Reviews
Michael Kassler. The decision of Arnold Schoenberg's twelve-note-class system and related systems. Clearinghouse for Federal Scientific and Technical Information, U.S. Department of Commerce, Springfield, Virginia, 1964, 166 pp. - Michael Kassler. A sketch of the use of formalized languages for the assertion of music. Perspectives of new music, vol. 1 no. 2 (1963), pp. 83–94.- Michael Kassler. Toward a theory that is the twelve-note-class system. Perspectives of new music, vol. 5 no. 2 (1967), pp. 1–80.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 576-577
-
- Article
- Export citation
Benjamin Boretz. Meta-variations: Studies in the foundations of musical thought (I). Perspectives of new music, vol. 8 no. 1 (1969), pp. 1–74. - Benjamin Boretz. Sketch of a musical system (Meta-variations, Part II). Perspectives of new music, vol. 8 no. 2(1970), pp. 49–111. - Benjamin Boretz. The construction of musical syntax (I). Perspectives of new music, vol. 9 no. 1 (1970), pp. 23–42. - Richard M. Martin. On the proto-theory of musical structure. Perspectives of new music, pp. 68–73. - Benjamin Boretz. Musical syntax (II). Perspectives of new music, vol. 10 no. 1 (1971), pp. 232–270.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 577-578
-
- Article
- Export citation
Bimal Krishna Matilal. Epistemology, logic, and grammar in Indian philosophical analysis. Mouton, The Hague and Paris 1971, 183 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 578-579
-
- Article
- Export citation
Herbert L. Searles. Foreword. Truth and meaning, by David Greenwood, Philosophical Library, New York 1957, pp. vii–viii. - David Greenwood. Truth and metalanguage. Truth and meaning, pp. 1–17. - David Greenwood. Meaning in natural languages. Truth and meaning, pp. 18–36. - David Greenwood. The completeness of the sentential calculus. Truth and meaning, pp. 37–46. - David Greenwood. On mathematical definition. Truth and meaning, pp. 47–56. - David Greenwood. The nature of probability statements. Truth and meaning, pp. 57–83. - David Greenwood. The pragmatic theory of truth. Truth and meaning, pp. 84–109.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 579-580
-
- Article
- Export citation
Jacques Bouveresse. Carnap, le langage et la philosophie. L'âge de la science, vol. 3 (1970), pp. 117–154.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 580-581
-
- Article
- Export citation
Rudolf Carnap and Richard C. Jeffrey. Introduction. Studies in inductive logic and probability, Volume I, edited by Rudolf Carnap and Richard C. Jeffrey, University of California Press, Berkeley, Los Angeles, and London, 1971, pp. 1–4. - Rudolf Carnap. Inductive logic and rational decisions. A modified and expanded version of XXXII 104(1). Studies in inductive logic and probability, pp. 5–31. - Rudolf Carnap. A basic system of inductive logic, Part I. Studies in inductive logic and probability, pp. 33–165. - Richard C Jeffrey. Probability measures and integrals. Studies in inductive logic and probability, pp. 167–223. - Jürgen Humburg. The principle of instantial relevance. Studies in inductive logic and probability, pp. 225–233. - Haim Gaifman. Applications of de Finetti's theorem to inductive logic. Studies in inductive logic and probability, pp. 235–251.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 581-583
-
- Article
- Export citation
Heinrich Behmann. Der Prädikatenkalkül mil limitierten Variablen. Grundlegung einer naturlichen exakten Logik. The journal of symbolic logic, vol. 24 no. 2 (for 1959, pub. 1960), pp. 112–140. - Heinrich Behmann. Das Russellsche Paradoxon und die formale Logik. Atti del XII Congresso Internazionale di Filosofia (Venezia, 12-18 settembre 1958), Volume quinto, Logica, gnoseologia, filosofia delta scienza, filosofia del linguaggio, Sansoni Editore, Florence 1960, pp. 45–54.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 583-584
-
- Article
- Export citation
Robert L. Martin. Toward a solution to the liar paradox. The philosophical review, vol. 76(1967), pp. 279–311. - Robert L. Martin. On Grelling's paradox. The philosophical review, vol. 77 (1968), pp. 321–331. - Bas C. van Fraassen. Presupposition, implication, and self-reference. The journal of philosophy, vol. 65 (1968), pp. 136–152. - Brian Skyrms. Return of the liar: three-valued logic and the concept of truth. American philosophical quarterly, vol. 7 (1970), pp. 153–161. - Robert L. Martin. Preface. The paradox of the liar, edited by Robert L. Martin, Yale University Press, New Haven and London 1970, p. vii.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 584-587
-
- Article
- Export citation
W. V. Quine. Philosophy of logic. Prentice-Hall, Inc., Englewood Cliffs, N.J., 1970, xvi + 109 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 587-588
-
- Article
- Export citation
Stephan Korner. The philosophy of mathematics. An introductory essay. Hutchinson and Co., Ltd., London 1960, 198 pp. Paperbound reprint, Harper torchbooks, Harper Brothers, New York 1962, 198 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 588-593
-
- Article
- Export citation
Stephen F. Barker. Realism as a philosophy of mathematics. Foundations of mathematics, Symposium papers commemorating the sixtieth birthday of Kurt Gödel, edited by Jack J. Bulloff, Thomas C. Holyoke, and S. W. Hahn, Springer-Verlag, Berlin, Heidelberg, and New York, 1969, pp. 1–9.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 593
-
- Article
- Export citation
Joseph Ullian. Mathematical objects. Philosophy of science, The Delaware seminar, Volume 1, 1961-1962, edited by Bernard Baumrin, Interscience Publishers, New York and London 1963, pp. 187–205.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 593-595
-
- Article
- Export citation
M. J. Charlesworth. Analytical philosophy. New Catholic encyclopedia, prepared by an editorial staff at the Catholic University of America, McGraw-Hill Book Company, New York etc. 1967, vol. 1, pp. 470–473.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 595
-
- Article
- Export citation
H. A. Nielsen. Antinomy. New Catholic encyclopedia, prepared by an editorial staff at the Catholic University of America, McGraw-Hill Book Company, New York etc. 1967, vol. 1, pp. 621-623.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 595
-
- Article
- Export citation
J. A. Ladrière. Axiomatic system. New Catholic encyclopedia, prepared by an editorial staff at the Catholic University of America, McGraw-Hill Book Company, New York etc. 1967, vol. 1, pp. 1140–1141.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 596
-
- Article
- Export citation

 the infinitary logic (as described in [K, p. 6] over
the infinitary logic (as described in [K, p. 6] over  is obtained from
is obtained from  and
and 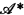 . Let
. Let 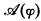 and
and 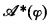 are
are 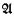 is a structure in which we can interpret
is a structure in which we can interpret