Survey/Expository Papers
A Symposium on Hilbert's Program
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 337
-
- Article
- Export citation
Hilbert's program sixty years later
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 338-348
-
- Article
- Export citation
Partial realizations of Hilbert's program
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 349-363
-
- Article
- Export citation
Hilbert's program relativized; Proof-theoretical and foundational reductions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 364-384
-
- Article
- Export citation
Research Article
Splitting P κλ into stationary subsets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 385-389
-
- Article
- Export citation
Addendum to “The truth is never simple”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 390-392
-
- Article
- Export citation
Strong measure zero sets and rapid filters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 393-402
-
- Article
- Export citation
Finite and finitely separable intermediate propositional logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 403-420
-
- Article
- Export citation
Extensions séparées et immédiates de corps valués
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 421-428
-
- Article
- Export citation
Where MA first fails
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 429-433
-
- Article
- Export citation
Des belles paires aux beaux uples
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 434-442
-
- Article
- Export citation
On infinite series of infinite isols
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 443-462
-
- Article
- Export citation
Quantifier elimination in separably closed fields of finite imperfectness degree
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 463-469
-
- Article
- Export citation
Algebraic extensions in nonstandard models and Hilbert's irreducibility theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 470-480
-
- Article
- Export citation
Believing the axioms. I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 481-511
-
- Article
- Export citation
Uncountable theories that are categorical in a higher power
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 512-530
-
- Article
- Export citation
Decidable discrete linear orders
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 531-539
-
- Article
- Export citation
Some filters of partitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 540-553
-
- Article
- Export citation
Uniqueness, definability and interpolation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 554-570
-
- Article
- Export citation
Survey/expository papers
Existentially closed algebras and boolean products
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 571-596
-
- Article
- Export citation

 for some
for some  some arithmetical
some arithmetical  and some positive
and some positive 
 with
with 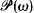 .
.

