Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-22T20:46:33.622Z Has data issue: false hasContentIssue false
  • English
  • Français

On infinite series of infinite isols

Published online by Cambridge University Press:  12 March 2014

Joseph Barback
Joseph Barback*
Affiliation:
Department of Mathematics, State University of New York College at Buffalo, Buffalo, New York 14222
Get access Rights & Permissions [Opens in a new window]

Extract

We are interested in regressive isols, recursive functions, and the extensions of recursive functions to the isols. One of the nicest concepts that has been applied to the study of these notions is of an infinite series of isols. J. C. E. Dekker introduced infinite series of isols in [3]. With this concept one may associate with each number theoretic function u and regressive isol B a value in the isols to correspond to the series

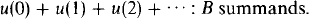
When u is chosen as a recursive function, or as a recursive combinatorial function, many of the sums that one associates with familiar finite series may be generalized to infinite series. For example, if B is any regressive isol, then

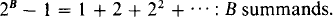
The results presented in our paper were motivated by an interest in extending infinite series to a setting where the terms being summed may be infinite isols. In our paper, we do this in a special way, as will be described below. We would first like to briefly comment on some facts about the concept of defining an infinite series in the isols.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 53 , Issue 2 , June 1988 , pp. 443 - 462
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barback, J., Contributions to the theory of isols, Ph.D. Thesis, Rutgers University, New Brunswick, New Jersey, 1964.Google Scholar
[2] Barback, J., Tame models in the isols, Houston Journal of Mathematics, vol. 12 (1986), pp. 163–175.Google Scholar
[3] Dekker, J. C. E., Infinite series of isols, In: Recursive function theory, Proceedings of Symposia in Pure Mathematics, vol. 5, American Mathematical Society, Providence, Rhode Island, 1962, pp. 77–96.CrossRefGoogle Scholar
[4] Dekker, J. C. E., Les fonctions combinatoires et les isols, Collection de Logique Mathématique, ser. A, No. 22, Gauthier-Villars, Paris, 1966.Google Scholar
[5] Ellentuck, E., Universal isols, Mathematische Zeitschrift, vol. 98 (1967), pp. 1–8.CrossRefGoogle Scholar
[6] Ellentuck, E., Diagonal methods in the theory of isols, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 26 (1980), pp. 193–204.CrossRefGoogle Scholar
[7] Gersting, J., A rate of growth criterion for universality of regressive isols, Pacific Journal of Mathematics, vol. 31 (1969), pp. 669–677.CrossRefGoogle Scholar
[8] McLaughlin, T. G., Regressive sets and the theory of isols. Marcel Dekker, New York, 1982.Google Scholar
[9] McLaughlin, T. G., Nerode semirings and Barback‘s “Tame Models”, Houston Journal of Mathematics, vol. 12 (1986), pp. 211–223.Google Scholar
[10] Nerode, A., Diophantine correct non-standard models in the isols, Annals of Mathematics, ser. 2, vol. 84 (1966), pp. 421–432.CrossRefGoogle Scholar
[11] Sansone, F., The backward and forward summation of infinite series of isols, Mathematica Scandinavica, vol. 24 (1969), pp. 217–220.CrossRefGoogle Scholar
[12] Skolem, T., Peano‘s axioms and models of arithmetic, Selected works in logic (Fenstad, J. E., editor), Universitetsforlaget, Oslo, 1970, 587–600.Google Scholar