Research Article
Lattice embeddings into the recursively enumerable degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 257-272
-
- Article
- Export citation
A generalization of the limit lemma and clopen games
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 273-291
-
- Article
- Export citation
Combinatorial and recursive aspects of the automorphism group of the countable atomless Boolean algebra
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 292-301
-
- Article
- Export citation
On the number of nonisomorphic models of an infinitary theory which has the infinitary order property. Part A
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 302-322
-
- Article
- Export citation
Maximal chains in the fundamental order
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 323-326
-
- Article
- Export citation
Finest partitions for ultrafilters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 327-332
-
- Article
- Export citation
Errata
Replacement and collection: a correction
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 333
-
- Article
-
- You have access
- Export citation
Research Article
Périodicité des théories élémentaires des corps de séries formelles itérées
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 334-351
-
- Article
- Export citation
On the Kleene degrees of Π 1 1 sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 352-359
-
- Article
- Export citation
On the relation between choice and comprehension principles in second order arithmetic1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 360-373
-
- Article
- Export citation
Theories with finitely many models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 374-376
-
- Article
- Export citation
On the strength of nonstandard analysis
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 377-386
-
- Article
- Export citation
Flagg realizability in arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 387-392
-
- Article
- Export citation
Natural deduction based set theories: a new resolution of the old paradoxes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 393-411
-
- Article
- Export citation
Prime models and almost decidability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 412-420
-
- Article
- Export citation
ω 1-like recursively saturated models of Presburger's arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 421-429
-
- Article
- Export citation
Recursive categoricity and persistence
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 430-434
-
- Article
- Export citation
The inclusion-exclusion principle for finitely many isolated sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 435-447
-
- Article
- Export citation
An interpolation theorem in many-valued logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 448-452
-
- Article
- Export citation
Σ 1 definitions with parameters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 453-461
-
- Article
- Export citation

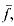 , where
, where 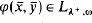 . Now define
. Now define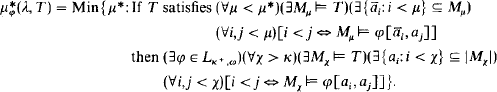
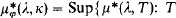 is a theory in
is a theory in 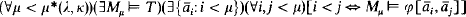
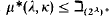 . Here we continue that work by proving
. Here we continue that work by proving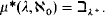 .
.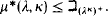 .
.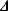 ⊆
⊆ 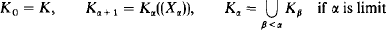
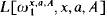 . This reducibility induces an equivalence relation ≡
. This reducibility induces an equivalence relation ≡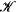 be the structure that consists of the Kleene degrees and the induced partial order
be the structure that consists of the Kleene degrees and the induced partial order 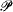 , the Kleene degrees of the
, the Kleene degrees of the  sets of reals. If sharps exist, then there is not much to
sets of reals. If sharps exist, then there is not much to 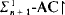 and
and 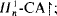 ; the proof does not use Skolem theories.
; the proof does not use Skolem theories.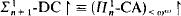 , for suitable classes of sentences;
, for suitable classes of sentences;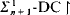 proves the consistency of
proves the consistency of 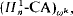 , for finite
, for finite 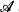 and ℬ be two structures for
and ℬ be two structures for 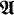 is such a model then the following is readily seen (as explained also in §1):
is such a model then the following is readily seen (as explained also in §1):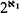
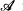 is
is 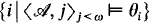 is recursive, where
is recursive, where 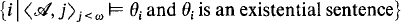 and
and