Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-16T16:48:28.816Z Has data issue: false hasContentIssue false
  • English
  • Français

ω 1-like recursively saturated models of Presburger's arithmetic

Published online by Cambridge University Press:  12 March 2014

Victor Harnik
Victor Harnik*
Affiliation:
Department of Mathematics, University of Haifa, Haifa, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

Let Pr be Presburger's arithmetic, i.e., the complete theory of the structure (ω, +). Lipshitz and Nadel showed in [4] that a countable model of Pr is recursively saturated iff it can be expanded to a model of Peano arithmetic, PA. As a starting point for an introductory discussion, let us mention one more fact about countable recursively saturated models of Pr. If 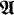is such a model then the following is readily seen (as explained also in §1):

Any two countable recursively saturated elementary endextensions of 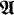are isomorphic.

If we drop “countable” from the assumption of this statement, we can still say that the two models are ∞ω-equivalent. Must they be isomorphic if both have cardinality ℵ1? Certainly not, since one of the models can be ω 1-like while the other is not. Once we realized this much, let us concentrate on ω 1-like structures. We prove in §3:

Theorem. Any countable recursively saturated model 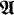of Pr has 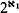isomorphism types of ω 1-like recursively saturated elementary endextensions. Only one of these is the isomorphism type of a structure that can be expanded to a model of PA.

The key technical result is proven in §2. It says that an 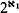as above has precisely two countable recursively saturated elementary endextensions which are nonisomorphic over .

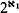Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 2 , June 1986 , pp. 421 - 429
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barwise, J. and Schlipf, J. S., An introduction to recursively saturated and resplendent models, this Journal, vol. 41 (1976), pp. 531–536.Google Scholar
[2] Enderton, H. B., A mathematical introduction to logic, Academic Press, New York, 1972.Google Scholar
[3] Jensen, D. and Ehrenfeucht, A., Some problems in elementary arithmetics, Fundamenta Mathematicae, vol. 92 (1976), pp. 223–245.CrossRefGoogle Scholar
[4] Lipshitz, L. and Nadel, M., The additive structure of models of arithmetic, Proceedings of the American Mathematical Society, vol. 68 (1978), pp. 331–336.CrossRefGoogle Scholar
[5] MacDowell, R. and Specker, E., Modelle der Arithmetik, Infinitistic Methods (Symposium, Warsaw, 1959), PWN, Warsaw, and Pergamon Press, Oxford, 1961, pp. 257–263.Google Scholar
[6] Morley, M. and Vaught, R., Homogeneous universal models, Mathematica Scandinavica, vol. 11 (1962), pp. 37–57.CrossRefGoogle Scholar
[7] Nadel, M., On a problem of MacDowell and Specker, this Journal, vol. 45 (1980), pp. 612–622.Google Scholar
[8] Nadel, M., The completeness of Peano multiplication, Israel Journal of Mathematics, vol. 39 (1981), pp. 225–233.CrossRefGoogle Scholar
[9] Ressayre, J.-P., Models with compactness properties relative to an admissible language, Annals of Mathematical Logic, vol. 11 (1977), pp. 31–55.CrossRefGoogle Scholar
[10] Schmerl, J. H., Peano models with many generic classes, Pacific Journal of Mathematics, vol. 46 (1973), pp. 523–536; erratum, J. H. Schmerl, Peano models with many generic classes, Pacific Journal of Mathematics , vol. 92 (1981), pp. 195–198.CrossRefGoogle Scholar
[11] Simpson, S. G., Forcing and models of arithmetic, Proceedings of the American Mathematical Society, vol. 43 (1974), pp. 193–194.CrossRefGoogle Scholar