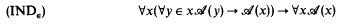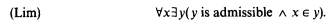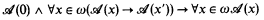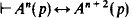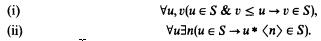Research Article
Functors and ordinal notations. I: A functorial construction of the veblen hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 713-729
-
- Article
- Export citation
An interpretation of Martin-Löf's type theory in a type-free theory of propositions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 730-753
-
- Article
- Export citation
Self-reference with negative types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 754-773
-
- Article
- Export citation
Monotone reducibility and the family of infinite sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 774-782
-
- Article
- Export citation
Which set existence axioms are needed to prove the Cauchy/Peano theorem for ordinary differential equations?
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 783-802
-
- Article
- Export citation
Deux remarques à propos de la propriété de recouvrement fini
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 803-807
-
- Article
- Export citation
Strongly compact cardinals, elementary embeddings and fixed points
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 808-812
-
- Article
- Export citation
Idempotent ideals on abelian groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 813-817
-
- Article
- Export citation
Register machine proof of the theorem on exponential diophantine representation of enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 818-829
-
- Article
- Export citation
C.c.c. forcing without combinatorics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 830-832
-
- Article
- Export citation
Complexity of κ-ultrafilters and inner models with measurable cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 833-841
-
- Article
- Export citation
An undecidable problem in finite combinatorics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 842-850
-
- Article
- Export citation
Intuitionistic fuzzy logic and intuitionistic fuzzy set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 851-866
-
- Article
- Export citation
The strength of admissibility without foundation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 867-879
-
- Article
- Export citation
Regular types in nonmultidimensional ω-stable theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 880-891
-
- Article
- Export citation
On the period of sequences (An(p)) in intuitionistic propositional calculus
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 892-899
-
- Article
- Export citation
Characteristically simple ℵ0-categorical groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 900-907
-
- Article
- Export citation
On choice sequences determined by spreads
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 908-916
-
- Article
- Export citation
Inconsistent models for relevant arithmetics1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 917-929
-
- Article
- Export citation
Kueker's conjecture for superstable theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 930-934
-
- Article
- Export citation

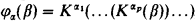 , with
, with 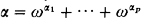 (not necessarily a Cantor normal form) and
(not necessarily a Cantor normal form) and  sets are all reducible to the (
sets are all reducible to the (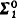 but not
but not 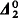 sets, which are all in turn reducible to the strictly
sets, which are all in turn reducible to the strictly 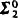 sets. In addition, the nontrivial
sets. In addition, the nontrivial  sets all have the same degree for
sets all have the same degree for 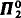 monotone sets which have different monotone degrees. We show that every
monotone sets which have different monotone degrees. We show that every 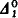 comprehension and
comprehension and 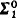 induction. Our main result is that, over RCA
induction. Our main result is that, over RCA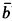 de
de 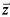 ), …,
), …, 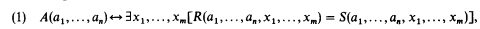
 -generic conditions. This characterisation can be applied to get simple proofs of many facts about c.c.c. forcing including Con(MA + ┐CH).
-generic conditions. This characterisation can be applied to get simple proofs of many facts about c.c.c. forcing including Con(MA + ┐CH).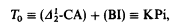
 -CA) + (BI) is the usual system of second order arithmetic with the axiom of
-CA) + (BI) is the usual system of second order arithmetic with the axiom of