Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T20:16:49.370Z Has data issue: false hasContentIssue false
  • English
  • Français

Which set existence axioms are needed to prove the Cauchy/Peano theorem for ordinary differential equations?

Published online by Cambridge University Press:  12 March 2014

Stephen G. Simpson
Stephen G. Simpson*
Affiliation:
Pennsylvania State University, University Park, Pennsylvania 16802
Get access Rights & Permissions [Opens in a new window]

Abstract

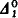We investigate the provability or nonprovability of certain ordinary mathematical theorems within certain weak subsystems of second order arithmetic. Specifically, we consider the Cauchy/Peano existence theorem for solutions of ordinary differential equations, in the context of the formal system RCA0 whose principal axioms are comprehension and 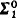induction. Our main result is that, over RCA0, the Cauchy/Peano Theorem is provably equivalent to weak König's lemma, i.e. the statement that every infinite {0, 1}-tree has a path. We also show that, over RCA0, the Ascoli lemma is provably equivalent to arithmetical comprehension, as is Osgood's theorem on the existence of maximum solutions. At the end of the paper we digress to relate our results to degrees of unsolvability and to computable analysis.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 3 , September 1984 , pp. 783 - 802
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aberth, O., The failure in computable analysis of a classical existence theorem of differential equations, Proceedings of the American Mathematical Society, vol. 30 (1971), pp. 151–156.CrossRefGoogle Scholar
[2]Aberth, O., Computable analysis, McGraw-Hill, New York, 1980.Google Scholar
[3]Arzelà, C., Funzioni di linee, Atti della Reale Accademia del Lincei. Rendiconti, ser. 4, vol. 5 (1889), part 1, pp. 342–348.Google Scholar
[4]Coddington, E. A. and Levinson, N.. Theory of ordinary differential equations, McGraw-Hill, New York, 1955.Google Scholar
[5]Friedman, H., Some systems of second order arithmetic and their use, Proceedings of the International Congress of Mathematicians (Vancouver, 1974), Vol. 1, Canadian Mathematical Congress, Montréal, 1975, pp. 235–242.Google Scholar
[6]Friedman, H., Systems of second order arithmetic with restricted induction. I, II (abstracts), this Journal, vol. 41 (1976), pp. 557–558, 558–559.Google Scholar
[7]Friedman, H., McAloon, K. and Simpson, S. G., A finite combinatorial principle which is equivalent to the 1-consistency of predicative analysis, Logic Symposion I (Patras, Greece, 1980) (Metakides, G., editor), North-Holland, Amsterdam, 1982, pp. 197–230.CrossRefGoogle Scholar
[8]Friedman, H., On fragments of Peano arithmetic, preprint, 1979.Google Scholar
[9]Friedman, H., Simpson, S. G. and Smith, R., Countable algebra and set existence axioms, Annals of Pure and Applied Logic, vol. 25 (1983), pp. 141–181.CrossRefGoogle Scholar
[10]Hilbert, D. and Bernays, P., Grundlagen der Mathematik. Vols. I, II. Springer-Verlag, Berlin, 1934, 1939.Google Scholar
[11]Jockusch, C. G. and Soare, R. I., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[12]Kirby, L. and Paris, J., Initial segments of models of Peano's axioms, Set theory and hierarchy theory. V (Proceedings of the Third Conference, Bierutowice, Poland, 1976), Lecture Notes in Mathematics, vol. 619, Springer-Verlag, Berlin, 1977, pp. 211–226.Google Scholar
[13]Kirby, L. and Paris, J., Σ n collection schemes in arithmetic, Logic Colloquium '77, North-Holland, Amsterdam, 1978, pp. 199–209.Google Scholar
[14]Kreisel, G., Hilbert's programme, Philosophy of mathematics (Benacerraf, P. and Putnam, H., editors), Prentice-Hall, Englewood Cliffs, N.J., 1964, pp. 157–180.Google Scholar
[15]Metakides, G., Nerode, A. and Shore, R., Recursive content of the Hahn-Banach theorem, Recursion theory (Proceedings of the American Mathematical Society Summer Institute, Cornell University, Ithaca, New York, 1982), Proceedings of Symposia in Pure Mathematics, American Mathematical Society, Providence, R.I. (to appear).Google Scholar
[16]Moschovakis, Y. N., Recusive analysis, Ph.D. thesis, University of Wisconsin, Madison, Wisconsin, 1963.Google Scholar
[17]Osgood, W. F., Beweis der Existenz einer Lösung der Differentialgleichung dy/dx = f(x, y) ohne Hinzunahme der Cauchy-Lipschitz'schen Bedingung, Monatshefte für Mathematik und Physik, vol. 9 (1898), pp. 331–345; abriged English translation, A source book in classical analysis (G. Birkhoff, editor), Harvard University Press, Cambridge, Massachusetts, 1973, pp. 251–258.CrossRefGoogle Scholar
[18]Paris, J. B., A hierarchy of cuts in models of arithmetic, Model theory of algebra and arithmetic (Proceedings of the Conference on Applications of Logic to Algebra and Arithmetic, Karpacz, 1979), Lecture Notes in Mathematics, vol. 834, Springer-Verlag, Berlin, 1980, pp. 312–337.Google Scholar
[19]Peano, G., Démonstration de l'intégrabilité des équations différentielles ordinaires, Mathematische Annalen, vol. 37 (1890), pp. 182–228.CrossRefGoogle Scholar
[20]Pour-El, M. B. and Richards, I., A computable ordinary differential equation which possesses no computable solution, Annals of Mathematical Logic, vol. 17 (1979), pp. 61–91.CrossRefGoogle Scholar
[21]Pour-El, M. B., Computability and noncomputability in classical analysis, preprint, 1980.Google Scholar
[22]Scott, D., Algebras of sets binumerable in complete extensions of arithmetic, Recursive function theory, Proceedings of Symposia in Pure Mathematics, vol. 5, American Mathematical Society, Providence, R.I., 1962, pp. 117–121.CrossRefGoogle Scholar
[23]Shore, R. A., The structure of the degrees of unsolvability, Recursion theory (Proceedings of the American Mathematical Society Summer Institute, Cornell University, Ithaca, New York, 1982), Proceedings of Symposia in Pure Mathematics, American Mathematical Society, Providence, R.I. (to appear).Google Scholar
[24]Simpson, S. G., Notes on subsystems of analysis, unpublished lecture notes, University of California, Berkeley, California, 1973.Google Scholar
[25]Simpson, S. G., Degrees of unsolvability: a survey of results, Handbook of mathematical logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 631–652.CrossRefGoogle Scholar
[26]Simpson, S. G., and transfinite induction, Logic Colloquium '80, North-Holland, Amsterdam, 1982, pp. 239–253.Google Scholar
[27]Simpson, S. G., Subsystems of second order arithmetic, in preparation.Google Scholar
[28]Steel, J., Determinateness and subsystems of analysis, Ph.D. Thesis, University of California, Berkeley, California, 1977.Google Scholar
[29]Weyl, H., Das Kontinuum: Kritische Untersuchungen über der Grundlagen der Analysis, Veit & Co., Leipzig, 1918; reprint, H. Weyl, E. Landau and B. Riemann, Das Kontinuum, und andere Monographien, Chelsea, New York, 1960, 1973.CrossRefGoogle Scholar