When studying the model theory of
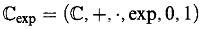
the first observation is that the integers can be defined as
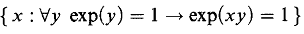
Since ∂exp is subject to all of Gödel's phenomena, this is often also the last observation. After Wilkie proved that ℝexp is model complete, one could ask the same question for ∂exp, but the answer is negative.
Proposition 1.1. ∂expis not model complete
Proof. If ∂exp is model complete, then every definable set is a projection of a closed set. Since ∂ is locally compact, every definable set is Fσ. The same is true for the complement, so every definable set is also Gδ. But, since ℤ is definable, ℚ is definable and a standard corollary of the Baire Category Theorem tells us that ℚ is not Gδ.
Still, there are several interesting open questions about ∂exp.
• Is ℝ definable in ∂exp?
• (quasiminimality) Is every definable set countable or co-countable? (Note that this is true in the structure (∂, ℤ, +, ·) where we add a predicate for ℤ).
• (Mycielski) Is there an automorphism of ∂exp other than the identity and complex conjugation?1
A positive answer to the first question would tell us that ∂exp is essentially second order arithmetic, while a positive answer to the second would say that integers are really the only obstruction to a reasonable theory of definable sets.
A fascinating, novel approach to ∂exp is provided by Zilber's [6] pseudoexponentiation. Let L be the language {+, · E, 0, 1}.
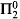 nullsets
nullsets