Research Article
Classifying Borel automorphisms
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1081-1092
-
- Article
- Export citation
Cellularity and the structure of pseudo-trees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1093-1107
-
- Article
- Export citation
Groups definable in ordered vector spaces over ordered division rings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1108-1140
-
- Article
- Export citation
Fondements de la logique positive
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1141-1162
-
- Article
- Export citation
Stable definability and generic relations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1163-1176
-
- Article
- Export citation
O-minimal spectra, infinitesimal subgroups and cohomology
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1177-1193
-
- Article
- Export citation
QL(ℂn) determines n
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1194-1196
-
- Article
- Export citation
On the complexity of alpha conversion
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1197-1203
-
- Article
- Export citation
Intuitionistic logic freed of all metarules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1204-1218
-
- Article
- Export citation
Maximal chains in the Turing degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1219-1227
-
- Article
- Export citation
There may be infinitely many near-coherence classes under u < ∂
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1228-1238
-
- Article
- Export citation
Flag algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1239-1282
-
- Article
- Export citation
Relational structures constructible by quantifier free definable operations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1283-1298
-
- Article
- Export citation
The ground axiom
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1299-1317
-
- Article
- Export citation
A note on subsystems of open induction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1318-1322
-
- Article
- Export citation
Winning the pressing down game but not Banach-Mazur
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1323-1335
-
- Article
- Export citation
The complexity of resolution refinements
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1336-1352
-
- Article
- Export citation
Consequences of the provability of NP ⊆ P/poly
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1353-1371
-
- Article
- Export citation
Increasing δ21 and Namba-style forcing
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1372-1378
-
- Article
- Export citation
The pseudocompactness of [0.1] is equivalent to the uniform continuity theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1379-1384
-
- Article
- Export citation

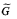 of
of 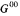 is acyclic in Čech cohomology and Ψ is an isomorphism. Finally we prove the conjecture in some special cases.
is acyclic in Čech cohomology and Ψ is an isomorphism. Finally we prove the conjecture in some special cases.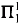 [
[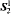 proves
proves 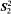 proves
proves 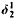 while preserving
while preserving