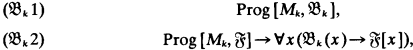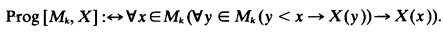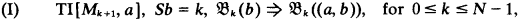Research Article
On the inconsistency of systems similar to

-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-2
-
- Article
- Export citation
First steps in intuitionistic model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 3-12
-
- Article
- Export citation
Controlling the dependence degree of a recursively enumerable vector space1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 13-22
-
- Article
- Export citation
Relativized realizability in intuitionistic arithmetic of all finite types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 23-44
-
- Article
- Export citation
Degrees of sensible lambda theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 45-55
-
- Article
- Export citation
Projective algebra and the calculus of relations1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 56-64
-
- Article
- Export citation
Saturated ideals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 65-76
-
- Article
- Export citation
Separation principles and the axiom of determinateness1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 77-81
-
- Article
- Export citation
The model theory of ordered differential fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 82-91
-
- Article
- Export citation
Rings which admit elimination of quantifiers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 92-112
-
- Article
- Export citation
Note on an induction axiom
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 113-117
-
- Article
- Export citation
Provable wellorderings of formal theories for transfinitely iterated inductive definitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 118-125
-
- Article
- Export citation
Existentially complete torsion-free nilpotent groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 126-134
-
- Article
- Export citation
Sets which do not have subsets of every higher degree1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 135-138
-
- Article
- Export citation
Reviews
Jon Barwise. Admissible sets and structures. An approach to definability theory. Perspectives in mathematical logic. Springer-Verlag, Berlin, Heidelberg, and New York, 1975, XIV + 394 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 139-144
-
- Article
- Export citation
M. A. Dickmann. Large infinitary languages. Model theory. Studies in logic and the foundations of mathematics, vol. 83. North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, xv+ 464 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 144-145
-
- Article
- Export citation
Aubert Daigneault. Introduction. Studies in algebraic logic, edited by Aubert Daigneault, Studies in mathematics, vol. 9, The Mathematical Association of America, [Washington, D.C.], 1974, pp. 1–5. - William Craig. Unification and abstraction in algebraic logic. Studies in algebraic logic, edited by Aubert Daigneault, Studies in mathematics, vol. 9, The Mathematical Association of America, [Washington, D.C.], 1974, pp. 6–57. - J. Donald Monk. Connections between combinatorial theory and algebraic logic. Studies in algebraic logic, edited by Aubert Daigneault, Studies in mathematics, vol. 9, The Mathematical Association of America, [Washington, D.C.], 1974, pp. 58–91. - Helena Rasiowa. Post algebras as a semantic foundation of m-valued logics. Studies in algebraic logic, edited by Aubert Daigneault, Studies in mathematics, vol. 9, The Mathematical Association of America, [Washington, D.C.], 1974, pp. 92–142. - Gonzalo E. Reyes. From sheaves to logic. Studies in algebraic logic, edited by Aubert Daigneault, Studies in mathematics, vol. 9, The Mathematical Association of America, [Washington, D.C.], 1974, pp. 143–204.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 145-147
-
- Article
- Export citation
Paul Bernays. Vorwort. Abhandlungen zur Philosophie der Mathematik, von Paul Bernays, Wissenschaftliche Buchgesellschaft, Darmstadt1976, S. VII–X.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 147
-
- Article
- Export citation
Paul Bernays. Probleme der theoretischen Logik. Neudruck von 2877. Ebd., S. 1–16.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 147-153
-
- Article
- Export citation
Helena Rasiowa. Introduction to modern mathematics. English translation of Wstęp do matematyki współczesnej by Olgierd Wojtasiewicz. North-Holland Publishing Company, Amsterdam and London, and American Elsevier Publishing Company, Inc., New York, 1973, xii + 339 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 153-154
-
- Article
- Export citation


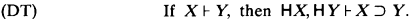

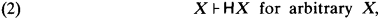

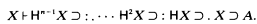
 is the λ-theory axiomatized by the set {
is the λ-theory axiomatized by the set { is Π
is Π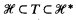 and 2
and 2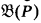 is the associated cBa. We write
is the associated cBa. We write 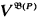 .
.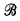 is κ-complete iff sups of subsets of
is κ-complete iff sups of subsets of 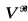 representing
representing 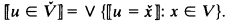
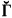 , the class dual to Γ, consist of the complements relative to
, the class dual to Γ, consist of the complements relative to 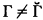 , then let
, then let 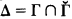 . A continuously closed nonselfdual class Γ of subsets of
. A continuously closed nonselfdual class Γ of subsets of 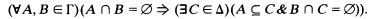
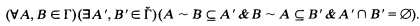
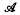 be the class of finite fields. Let
be the class of finite fields. Let 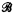 be the class of 2 × 2 matrix rings over a field with a prime number of elements. Let
be the class of 2 × 2 matrix rings over a field with a prime number of elements. Let 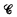 be the class of rings of the form
be the class of rings of the form 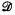 be the set of ordered pairs (
be the set of ordered pairs (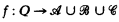 such that the characteristic of the ring
such that the characteristic of the ring 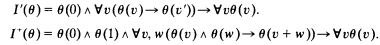
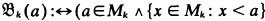 is wellordered) with
is wellordered) with  are definable in ID
are definable in ID