Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T05:21:26.114Z Has data issue: false hasContentIssue false
  • English
  • Français

Separation principles and the axiom of determinateness1

Published online by Cambridge University Press:  12 March 2014

Robert A. van Wesep
Robert A. van Wesep*
Affiliation:
University of California, Berkeley, Berkeley, California 94720 California Institute of Technology, Pasadena, California 91125
Get access Rights & Permissions [Opens in a new window]

Extract

Let Γ be a class of subsets of Baire space (ωω) closed under inverse images by continuous functions. We say such a Γ is continuously closed. Let 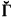, the class dual to Γ, consist of the complements relative to ωω of members of Γ. If Γ is not selfdual, i.e., 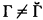, then let . A continuously closed nonselfdual class Γ of subsets of ωΓ is said to have the first separation property [2] if

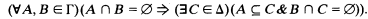
The set C is said to separate A and B. The class Γ is said to have the second separation property [3] if

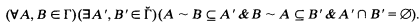
We shall assume the axiom of determinateness and show that if Γ is a continuously closed class of subsets of ωω and 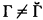then

(1) Γ has the first separation property iff 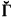does not have the second separation property, and

(2) either Γ or 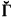has the second separation property.

Of course, (1) and (2) taken together imply that Γ and 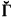cannot both have the first separation property.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 1 , March 1978 , pp. 77 - 81
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This paper represents research done at the University of California, Berkeley, under the guidance of Professor J. W. Addison. It is part of the author's Ph.D. thesis. The author wishes to thank Professor Addison for his guidance and encouragement.

References

BIBLIOGRAPHY

[1]Kuratowski, C., Sur les théorèmes de séparation dans la théorie des ensembles, Fundamenta Mathematicae, vol. 26 (1936), pp. 183–191.CrossRefGoogle Scholar
[2]Lusin, N., Sur les ensembles analytiques, Fundamenta Mathematicae, vol. 10 (1927).CrossRefGoogle Scholar
[3]Lusin, N., Leçons sur les ensembles analytiques et leurs applications, Gauthier-Villars, Paris, 1930.Google Scholar
[4]Martin, D. A., The Wadge ordering is a well-ordering, unpublished manuscript.Google Scholar
[5]Steel, J., Subsystems of analysis and the axiom of determinateness. Thesis, University of California, Berkeley, 1976.Google Scholar
[6]Van Wesep, R., Subsystems of analysis, and descriptive set theory under the axiom of determinateness, Thesis, University of California, Berkeley, 1977.Google Scholar
[7]Wadge, W., Degrees of complexity of subsets of the Baire space, Notices of the American Mathematical Society, vol. 19 (1972), p. 714.Google Scholar