Let T1 be the complete first-order theory of the additive group of the integers with 1 as distinguished element (in symbols, T1 = Th(Z, +, 1)). In this paper we prove that all models of T1 are ℵ0-homogeneous (§2), classify them (and lists of elements in them) up to isomorphism or L∞κ-equivalence (§§3 and 4) and show that they may be as complex as arbitrary sets of real numbers from the point of view of admissible set theory (§5). The results of §§2 and 5 together show that while the Scott heights of all models of T1 are ≤ ω (by ℵ0-homogeneity) their HYP-heights form an unbounded subset of the cardinal .

In addition to providing this unusual example of the relation between Scott heights and HYP-heights, the theory T1 has served (using the homogeneity results of §2) as an example for certain combinations of properties that people had looked for in stability theory (see end of §4). In §6 it is shown that not all models of T = Th(Z, +) are ℵ0-homogeneous, so that the availability of the constant for 1 is essential for the result of §2.

The two main results of this paper (2.2 and essentially Theorem 5.3) were obtained in the summer of 1979. Later we learnt from Victor Harnik and Julia Knight that T1 is of some interest for stability theory, and were encouraged to write up our proofs.

During 1982/3 we improved the proofs and added some results.

For e.g. λ = μ+, μ regular, λ larger than the continuum, we prove a strong nonpartition result (stronger than λ → [λ; λ]2). As a consequence, the product of two topological spaces of cellularity <λ may have cellularity λ, or, in equivalent formulation, the product of two λ-c.c. Boolean algebras may lack the λ-c.c. Also λ-S-spaces and λ-L-spaces exist. In fact we deal not with successors of regular λ but with regular λ above the continuum which has a nonreflecting stationary subset of ordinals with uncountable cofinalities; sometimes we require λ to be not strong limit.

The paper is self-contained. On the nonpartition results see the closely related papers of Todorčević [T1], Shelah [Sh276] and [Sh261], and Shelah and Steprans [ShSt1].

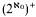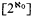On the cellularity of products see Todorčević [T2] and [T3], where such results were obtained for (e.g.) cf and 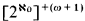; the class of cardinals he gets is quite disjoint from ours. In [Sh282] such results were obtained for more successors of singulars (mainly λ+, λ > 2cf λ). Also, concerning S and L spaces, Todorčević gets existence.

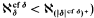Todorčević's work on cardinals like relies on [Sh68] (see more in [ShA2, Chapter XIII]) (the scales appearing in the proof of ). The problem was stressed in a preliminary version of the surveys of Juhasz and Monk. We give a detailed proof for one strong nonpartition theorem (1.1) and then give various strengthenings. We then use 1.10 to get the consequences (in 1.11 and 1.12).

We study increasing F-sequences, where F is a dilator: an increasing F-sequence is a sequence (indexed by ordinal numbers) of ordinal numbers, starting with 0 and terminating at the first step x where F(x) is reached (at every step x + 1 we use the same process as in decreasing F-sequences, cf. [2], but with “+ 1” instead of “−1”). By induction on dilators, we shall prove that every increasing F-sequence terminates and moreover we can determine for every dilator F the point where the increasing F-sequence terminates.

We apply these results to inverse Goodstein sequences, i.e. increasing (1 + Id)(ω)-sequences. We show that the theorem

(a combinatorial theorem about ordinal numbers) is not provable in ID1.

For a general presentation of the results stated in this paper, see [1].

We use notions and results concerning the category ON (ordinal numbers), dilators and bilators, summarized in [2, pp. 25–31].

It is the purpose of this paper to make explicit the connection between J.-Y. Girard's “linear logic” [4], and certain models for the logic of quantum mechanics, namely Mulvey's “quantales” [9]. This will be done not only in the case of commutative linear logic, but also in the case of a version of noncommutative linear logic suggested, but not fully formalized, by Girard in lectures given at McGill University in the fall of 1987 [5], and which for reasons which will become clear later we call “cyclic linear logic”.

For many of our results on quantales, we rely on the work of Niefield and Rosenthal [10].

The reader should note that by “the logic of quantum mechanics” we do not mean the lattice theoretic “quantum logics” of Birkhoff and von Neumann [1], but rather a logic involving an associative (in general noncommutative) operation “and then”. Logical validity is intended to embody empirical verification (whether a physical experiment, or running a program), and the validity of A & B (in Mulvey's notation) is to be regarded as “we have verified A, and then we have verified B”. (See M. D. Srinivas [11] for another exposition of this idea.)

This of course is precisely the view of the “multiplicative conjunction”, ⊗, in the phase semantics for Girard's linear logic [4], [5]. Indeed the quantale semantics for linear logic may be regarded as an element-free version of the phase semantics.

C. Karp has shown that if α is an ordinal with ωα = α and A is a linear ordering with a smallest element, then α and α ⊗ A are equivalent in L∞ω up to quantifer rank α. This result can be expressed in terms of Ehrenfeucht-Fraïssé games where player ∀ has to make additional moves by choosing elements of a descending sequence in α. Our aim in this paper is to prove a similar result for Ehrenfeucht-Fraïssé games of length ω1. One implication of such a result will be that a certain infinite quantifier language cannot say that a linear ordering has no descending ω1-sequences (when the alphabet contains only one binary relation symbol). Connected work is done by Hyttinen and Oikkonen in [H] and [O].

The two statements “Two different objects cannot occupy the same place at the same time” and “An object cannot be in two different places at the same time” are axioms of our everyday understanding of objects, space and time. We develop a first-order theory OST (Objects, Space and Time) in which formal equivalents of these two statements are taken as axioms. Using the theory OST, we uncover other fundamental principles of objects, space and time. We attempt to understand the logical nature of these principles, to investigate their formal consequences, and to identify logical alternatives to them. For easy reference, all of the nonlogical axioms of OST are listed together at the end of §2. In §3, we introduce two possible extensions of OST.

The condensed detachment rule, or ruleD, was first proposed by Carew Meredith in the 1950's for propositional logic based on implication. It is a combination of modus ponens with a “minimal” amount of substitution. We shall give a precise detailed statement of rule D. (Some attempts in the published literature to do this have been inaccurate.)

The D-completeness question for a given set of logical axioms is whether every formula deducible from the axioms by modus ponens and substitution can be deduced instead by rule D alone. Under the well-known formulae-as-types correspondence between propositional logic and combinator-based type-theory, rule D turns out to correspond exactly to an algorithm for computing principal type-schemes in combinatory logic. Using this fact, we shall show that D is complete for intuitionistic and classical implicational logic. We shall also show that D is incomplete for two weaker systems, BCK- and BCI-logic.

In describing the formulae-as-types correspondence it is common to say that combinators correspond to proofs in implicational logic. But if “proofs” means “proofs by the usual rules of modus ponens and substitution”, then this is not true. It only becomes true when we say “proofs by rule D”; we shall describe the precise correspondence in Corollary 6.7.1 below.

This paper is written for readers in propositional logic and in combinatory logic. Since workers in one field may not feel totally happy in the other, we include short introductions to both fields.

We wish to record thanks to Martin Bunder, Adrian Rezus and the referee for helpful comments and advice.

A reduction algebra is defined as a set with a collection of partial unary functions (called reduction operators). Motivated by the lambda calculus, the Church-Rosser property is defined for a reduction algebra and a characterization is given for those reduction algebras satisfying CRP and having a measure respecting the reductions. The characterization is used to give (with 20/20 hindsight) a more direct proof of the strong normalization theorem for the impredicative second order intuitionistic propositional calculus.

Although it is known that reachability in undirected finite graphs can be expressed by an existential monadic second-order sentence, our main result is that this is not the case for directed finite graphs (even in the presence of certain “built-in” relations, such as the successor relation). The proof makes use of Ehrenfeucht-Fraïssé games, along with probabilistic arguments. However, we show that for directed finite graphs with degree at most k, reachability is expressible by an existential monadic second-order sentence.

We define the notion of generic for an arbitrary subgroup H of a stable group, and show that H has a definable hull with the same generic properties. We then apply this to the theory of stable fields.

Kruskal proved that finite trees are well-quasi-ordered by hom(e)omorphic embeddability. Friedman observed that this statement is not provable in predicative analysis. Friedman also proposed (see in [Simpson]) some stronger variants of the Kruskal theorem dealing with finite labeled trees under hom(e)omorphic embeddability with a certain gap-condition, where labels are arbitrary finite ordinals from a fixed initial segment of ω. The corresponding limit statement, expressing that for all initial segments of ω these labeled trees are well-quasi-ordered, is provable in -CA, but not in the analogous theory -CA0 with induction restricted to sets. Schütte and Simpson proved that the one-dimensional case of Friedman's limit statement dealing with finite labeled intervals is not provable in Peano arithmetic. However, Friedman's gap-condition fails for finite trees labeled with transfinite ordinals. In [Gordeev 1] I proposed another gap-condition and proved the resulting one-dimensional modified statements for all (countable) transfinite ordinal-labels. The corresponding universal modified one-dimensional statement UM1 is provable in (in fact, is equivalent to) the familiar theory ATR0 whose proof-theoretic ordinal is Γ0. In [Gordeev 1] I also announced that, in the general case of arbitrarily-branching finite trees labeled with transfinite ordinals, in the proof-theoretic sense the hierarchy of the limit modified statements M<λ (which are denoted by LMλ in the present note) is as strong as the hierarchy of the familiar theories of iterated inductive definitions (more precisely, see [Gordeev 1, Concluding Remark 3]). In this note I present a “positive” proof of the full universal modified statement UM, together with a short proof of the crucial “reverse” results which is based on Okada's interpretation of the well-established ordinal notations of Buchholz corresponding to the theories of iterated inductive definitions. Formally the results are summarized in §5 below.

Mathematics is a natural science whose great generality makes many philosophers think of it as a supernatural science, consisting of truths derived independently of experience about objects not given in experience. Some mathematicians, like Simpson [16], try to defend mathematics from the resulting objection that it is merely a mental game by first conceding that most of it is meaningless and then trying to save what is left by some technical tour de force. Some physicists, like Wigner [20], admit that mathematics is applicable to the world, but declare themselves unable to understand what makes its applications possible. Both Simpson's worries and Wigner's puzzlement can be relieved if we assimilate mathematics more closely to the other natural sciences.

The program of reverse mathematics has usually been to find which parts of set theory, often used as a base for other mathematics, are actually necessary for some particular mathematical theory. In recent years, Slaman, Groszek, et al, have given the approach a new twist. The priority arguments of recursion theory do not naturally or necessarily lead to a foundation involving any set theory; rather, Peano Arithmetic (PA) in the language of arithmetic suffices. From this point, the appropriate subsystems to consider are fragments of PA with limited induction. A theorem in this area would then have the form that certain induction axioms are independent of, necessary for, or even equivalent to a theorem about the Turing degrees. (See, for examples, [C], [GS], [M], [MS], and [SW].)

As go the integers so go the ordinals. One motivation of α-recursion theory (recursion on admissible ordinals) is to generalize classical recursion theory. Since induction in arithmetic is meant to capture the well-foundedness of ω, the corresponding axiom in set theory is foundation. So reverse mathematics, even in the context of a set theory (admissibility), can be changed by the influence of reverse recursion theory. We ask not which set existence axioms, but which foundation axioms, are necessary for the theorems of α-recursion theory.

When working in the theory KP – Foundation Schema (hereinafter called KP−), one should really not call it α-recursion theory, which refers implicitly to the full set of axioms KP. Just as the name β-recursion theory refers to what would be α-recursion theory only it includes also inadmissible ordinals, we call the subject of study here γ-recursion theory. This answers a question by Sacks and S. Friedman, “What is γ-recursion theory?”

In the last years several research projects have been motivated by the problem of constructing the usual geometrical spaces by admitting “regions” and “inclusion” between regions as primitives and by defining the points as suitable sequences or classes of regions (for references see [2]).

In this paper we propose and examine a system of axioms for the pointless space theory in which “regions”, “inclusion”, “distance” and “diameter” are assumed as primitives and the concept of point is derived. Such a system extends a system proposed by K. Weihrauch and U. Schreiber in [5].

In the sequel R and N denote the set of real numbers and the set of natural numbers, and E is a Euclidean metric space. Moreover, if X is a subset of R, then ⋁X is the least upper bound and ⋀X the greatest lower bound of X.

This paper discusses six formalization techniques, of varying strengths, for extending a formal system based on traditional mathematical logic. The purpose of these formalization techniques is to simulate the introduction of new syntactic constructs, along with associated semantics for them. We show that certain techniques (among the six) subsume others. To illustrate sharpness, we also consider a selection of constructs and show which techniques can and cannot be used to introduce them. The six studied techniques were selected on the basis of actual practice in logic and computing. They do not form an exhaustive list.

We present a theory VF of partial truth over Peano arithmetic and we prove that VF and ID1, have the same arithmetical content. The semantics of VF is inspired by van Fraassen's notion of supervaluation.

This paper is a contribution to the following natural problem in complexity theory:

(*) Is there a complexity theory for isomorphism types of recursive countable relational structures? I.e. given a recursive relational structure ℛ over the set N of nonnegative integers, is there a nontrivial lower bound for the time-space complexity of recursive structures isomorphic (resp. recursively isomorphic) to ℛ?

For unary recursive relations R, the answer is trivially negative: either R is finite or coinfinite or 〈N, R〉 is recursively isomorphic to 〈N, {x ϵ N: x is even}〉.

The general problem for relations with arity 2 (or greater) is open.

Related to this problem, a classical result (going back to S. C. Kleene [4], 1955) states that every recursive ordinal is in fact primitive recursive.

In [3] Patrick Dehornoy, using methods relevant to computer science, improves this result, showing that every recursive ordinal can be represented by a recursive total ordering over N which has linear deterministic time complexity relative to the binary representation of integers. As he notices, his proof applies to every recursive total order type α such that the isomorphism type of α is not changed if points are replaced by arbitrary finite nonempty subsets of consecutive points.

In this paper we extend Dehornoy's result to all recursive total orderings over N and get minimal complexity for both time and space simultaneously.

We show that the following property (LN) holds in the basic Cohen model as sketched by Jech: The order topology of any linearly ordered set is normal. This proves the independence of the axiom of choice from LN in ZF, and thus settles a question raised by G. Birkhoff (1940) which was partly answered by van Douwen (1985).

In [vDF], van Douwen and Fleissner introduce a number of axioms which hold in models constructed by iteratively forcing MA in a nontrivial extension of the set-theoretic universe. One such model is the Bell-Kunen model, obtained by starting with a model of ZFC + GCH, then forcing “MA + ϲ = ω2” by the standard means, then forcing “MA + ϲ = ω3”, and so on. The Bell-Kunen model is the result of an ω1 sequence of extensions of this form, with direct limits taken at limit ordinals. (See [BK] for a more complete description.) Van Douwen and Fleissner observed that many of the properties of this model could be distilled into a “Definable Forcing Axiom”, which states that “If P is a c.c.c. 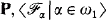partial order which is definable from a real, then there is a sequence of filters through , such that if 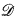is any dense subset of P, then all but countably many of the ℱα's meet in a nonempty set.” (They call such a sequence ω1-generic.) Van Douwen and Fleissner ask whether one can eliminate the restriction on the c.c.c. order entirely; the resulting axiom (“If P is any c.c.c. partial order of cardinality at most ϲ, then there is a sequence of filters…”) is called the Undefinable Forcing Axiom (UFA).

Many phrases have been used to express what are sometimes called anti-realist conceptions of truth: ‘verifiability’, ‘knowability’, ‘rational acceptability’, ‘warranted assertability’. In spite of their obvious differences, all four of these phrases have a common form; each is a cognitive attitude modified by ‘-ability’. They speak of the possibility of verification, knowledge, rational acceptance or warranted assertion. Schematically, it seems to be claimed that it is true that A if and only if it is possible that it is E'd that A, where ‘E’ is to be replaced by some cognitive verb and ‘A’ by any indicative sentence of the class to which the anti-realist conception is being claimed to apply. Since truth is redundant as a sentential operator, this boils down to the following thesis, where ‘p’ is a propositional variable and ‘M’ expresses the appropriate kind of possibility:

(*) also formalizes views such as Putnam's: ‘To claim a statement is true is to claim it could be justified’ [11, p. 56]. It is no doubt a crude model for anti-realism, but one has to start somewhere; by seeing how and why more sophisticated versions of anti-realism differ from (*) one should be able to understand them better too. Moreover, if an anti-realist rejects the equation of truth with, say, warranted assertibility, arguing that truth is rather to be identified with the possibility of getting into a position in which one's warrant to assert somehow cannot be overturned, the form of (*) is preserved, for truth is still being identified with the possibility of something.