Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T20:43:47.216Z Has data issue: false hasContentIssue false
  • English
  • Français

On models of the elementary theory of (Z, +, 1)

Published online by Cambridge University Press:  12 March 2014

Mark Nadel  and
Jonathan Stavi
Mark Nadel*
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, Indiana 46556
Jonathan Stavi
Affiliation:
Department of Mathematics, Bar Ilan University, Ramat Gan, Israel
*
Mitre Corporation, Burlington Road, Bedford, Massachusetts 01730
Get access Rights & Permissions [Opens in a new window]

Extract

Let T1 be the complete first-order theory of the additive group of the integers with 1 as distinguished element (in symbols, T1 = Th(Z, +, 1)). In this paper we prove that all models of T1 are ℵ0-homogeneous (§2), classify them (and lists of elements in them) up to isomorphism or L∞κ-equivalence (§§3 and 4) and show that they may be as complex as arbitrary sets of real numbers from the point of view of admissible set theory (§5). The results of §§2 and 5 together show that while the Scott heights of all models of T1 are ≤ ω (by ℵ0-homogeneity) their HYP-heights form an unbounded subset of the cardinal .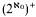

In addition to providing this unusual example of the relation between Scott heights and HYP-heights, the theory T1 has served (using the homogeneity results of §2) as an example for certain combinations of properties that people had looked for in stability theory (see end of §4). In §6 it is shown that not all models of T = Th(Z, +) are ℵ0-homogeneous, so that the availability of the constant for 1 is essential for the result of §2.

The two main results of this paper (2.2 and essentially Theorem 5.3) were obtained in the summer of 1979. Later we learnt from Victor Harnik and Julia Knight that T1 is of some interest for stability theory, and were encouraged to write up our proofs.

During 1982/3 we improved the proofs and added some results.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 55 , Issue 1 , March 1990 , pp. 1 - 20
Copyright
Copyright © Association for Symbolic Logic 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, J.et al., A “natural” theory without a prime model, Algebra Universalis, vol. 3 (1973), pp. 152–155.CrossRefGoogle Scholar
[2]Barwise, J., Admissible sets and structures, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
[3]Barwise, J. and Schlipf, J., An introduction to recursively saturated and resplendent models, this Journal, vol. 41 (1976), pp. 531–536.Google Scholar
[4]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[5]Eklof, P. and Fisher, E., The elementary theory of abelian groups, Annals of Mathematical Logic, vol. 4 (1972), pp. 115–171.CrossRefGoogle Scholar
[6]Enderton, H. B., A mathematical introduction to logic, Academic Press, New York, 1972.Google Scholar
[7]Feferman, S. and Vaught, R., The first order properties of algebraic systems, Fundamenta Mathematical, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[8]Fuchs, L., Infinite abelian groups. Vol. 1, Academic Press, New York, 1970.Google Scholar
[9]Knight, J., Theories whose resplendent models are homogeneous, Israel Journal of Mathematics, vol. 42 (1982), pp. 151–161.CrossRefGoogle Scholar
[10]Knight, J. and Nadel, M., Models of arithmetic and closed ideals, this Journal, vol. 47 (1983), pp. 833–840.Google Scholar
[11]Nadel, M. and Stavi, J., The pure part of HYP, this Journal, vol. 42 (1977), pp. 33–46.Google Scholar