Article contents
Théories complètes de paires de corps valués henseliens
Published online by Cambridge University Press: 12 March 2014
Extract
Un prolongement de l'étude d'une théorie T, dans le langage 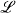 , consiste à s'intéresser à la théorie T* des paires de modèles de T, c'est-à-dire les structures de la forme (K ⊊ L) où K ⊨ T, L ⊨ T, K ≺ L, dans le langage
, consiste à s'intéresser à la théorie T* des paires de modèles de T, c'est-à-dire les structures de la forme (K ⊊ L) où K ⊨ T, L ⊨ T, K ≺ L, dans le langage 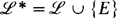 où E est un prédicat pour la sous-structure. Les propriétés de la théorie T ne se transmettent pas toujours à T*, particulièrement en ce qui concerne la complétude et la décidabilité. On trouve des illustrations de cas opposés dans les théories de corps:
où E est un prédicat pour la sous-structure. Les propriétés de la théorie T ne se transmettent pas toujours à T*, particulièrement en ce qui concerne la complétude et la décidabilité. On trouve des illustrations de cas opposés dans les théories de corps:
—si T est la théorie des corps algébriquement clos de caractéristique fixée, T* est complète et décidable;
—si T est la théorie des corps réels clos, T est complète et décidable, mais T* est indécidable, et admet 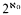 complétions différentes.
complétions différentes.
Nous allons nous intéresser ici aux paires de corps valués henseliens, et plus particulièrement au cas de caractéristique résiduelle nulle, de la forme (K ⊊ L, υ) où (K, υ) n'est pas nécessairement une sous-structure élémentaire de (L, υ). Ax, Kochen et Ershov ont montré que la théorie d'un corps valué henselien de caractéristique résiduelle nulle est entièrement déterminée par la théorie de son corps de restes et par la théorie de son groupe de valuation; par ailleurs, de résultats analogues existent pour certains corps de caractéristique résiduelle non nulle.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1990
References
RÉFÉRENCES
- 2
- Cited by


