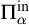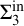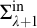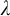1 Introduction
In this article we give a comprehensive Scott analysis of the class of linear orderings using three definitions of rank. Given a structure
![]() $\mathcal {A}$
, the (parameterless) Scott rank
$\mathcal {A}$
, the (parameterless) Scott rank
![]() $SR(\mathcal {A})$
is the least
$SR(\mathcal {A})$
is the least
![]() $\alpha $
such that the automorphism orbits of all tuples in
$\alpha $
such that the automorphism orbits of all tuples in
![]() $\mathcal {A}$
are
$\mathcal {A}$
are
![]() $\Sigma ^{\mathrm {in}}_{\alpha }$
definable; the parameterized Scott rank
$\Sigma ^{\mathrm {in}}_{\alpha }$
definable; the parameterized Scott rank
![]() $pSR(\mathcal {A})$
, is the least ordinal
$pSR(\mathcal {A})$
, is the least ordinal
![]() $\alpha $
such that there is a parameter
$\alpha $
such that there is a parameter
![]() $\bar p\in A^{<\omega }$
such that
$\bar p\in A^{<\omega }$
such that
![]() $SR((\mathcal {A},\bar p))=\alpha $
; and the Scott sentence complexity of
$SR((\mathcal {A},\bar p))=\alpha $
; and the Scott sentence complexity of
![]() $\mathcal {A}$
,
$\mathcal {A}$
,
![]() $SSC(\mathcal {A})$
is the least of the complexities
$SSC(\mathcal {A})$
is the least of the complexities
![]() $\Pi ^{\mathrm {in}}_{\alpha }$
,
$\Pi ^{\mathrm {in}}_{\alpha }$
,
![]() $\Sigma ^{\mathrm {in}}_{\alpha }$
,
$\Sigma ^{\mathrm {in}}_{\alpha }$
,
![]() $d\text{-}\Sigma ^{\mathrm {in}}_{\alpha }$
such that
$d\text{-}\Sigma ^{\mathrm {in}}_{\alpha }$
such that
![]() $\mathcal {A}$
has a Scott sentence of one of these complexities. The first two complexities were defined by Montalbán [Reference Montalbán19]. He showed that several notions of structural complexity coincide with these Scott ranks. The last notion was first formally investigated in [Reference Alvir, Knight and McCoy2]. While it does not assign an ordinal to structures, it was shown there that Scott sentence complexity is indeed a well-defined notion of rank. Table 1, taken from [Reference Montalbán22], shows the relationship between these invariants. As can be seen from the definitions of the two Scott ranks and Table 1, calculating the Scott sentence complexity of a structure comes down to calculating the complexity of the automorphism orbits of the structure’s tuples in all but the limit ordinal cases. The limit ordinal case is robustly treated for the first time in this article and we discuss it more in Section 2.
$\mathcal {A}$
has a Scott sentence of one of these complexities. The first two complexities were defined by Montalbán [Reference Montalbán19]. He showed that several notions of structural complexity coincide with these Scott ranks. The last notion was first formally investigated in [Reference Alvir, Knight and McCoy2]. While it does not assign an ordinal to structures, it was shown there that Scott sentence complexity is indeed a well-defined notion of rank. Table 1, taken from [Reference Montalbán22], shows the relationship between these invariants. As can be seen from the definitions of the two Scott ranks and Table 1, calculating the Scott sentence complexity of a structure comes down to calculating the complexity of the automorphism orbits of the structure’s tuples in all but the limit ordinal cases. The limit ordinal case is robustly treated for the first time in this article and we discuss it more in Section 2.
Table 1 [Reference Montalbán22, Table 1]. Relationship of the different Scott invariants. The last column contains the complexity of the automorphism orbit of the parameters involved in the parameterized Scott rank.

By calculating the Scott sentence complexities occurring in a class of structures we obtain a detailed picture of the descriptive complexity of its isomorphism relation. By the Lopez-Escobar theorem, a structure’s Scott sentence complexity corresponds to the Borel complexity of its isomorphism class. It is well known that the isomorphism relation on a class of structures is Borel if and only if the Scott ranks in the class are bounded below
![]() $\omega _1$
, see, for example, [Reference Gao12, Chapter 12].
$\omega _1$
, see, for example, [Reference Gao12, Chapter 12].
The class of linear orderings is a particularly interesting object of study as it is Borel complete: For every class of structures
![]() $\mathfrak {K}$
there is a Borel function
$\mathfrak {K}$
there is a Borel function
![]() $f:Mod(\mathfrak {K})\to Mod(\mathrm {LO})$
such that for all
$f:Mod(\mathfrak {K})\to Mod(\mathrm {LO})$
such that for all
![]() $\mathcal {A},\mathcal {B}\in \mathfrak {K}$
,
$\mathcal {A},\mathcal {B}\in \mathfrak {K}$
,
![]() $\mathcal {A}\cong \mathcal {B}$
if and only
$\mathcal {A}\cong \mathcal {B}$
if and only
![]() $f(\mathcal {A})\cong f(\mathcal {B})$
[Reference Friedman and Stanley8]. But the class of linear orderings is not complete for stronger forms of reduction such as faithful Borel reducibility or effective bi-interpretability [Reference Gao11]. If one dives into the realm of computable structure theory, one quickly sees that linear orderings are far from being “structurally complete”. For example, Richter’s result that no linear ordering can code a non-computable subset of
$f(\mathcal {A})\cong f(\mathcal {B})$
[Reference Friedman and Stanley8]. But the class of linear orderings is not complete for stronger forms of reduction such as faithful Borel reducibility or effective bi-interpretability [Reference Gao11]. If one dives into the realm of computable structure theory, one quickly sees that linear orderings are far from being “structurally complete”. For example, Richter’s result that no linear ordering can code a non-computable subset of
![]() $\omega $
in its isomorphism type, shows that linear orderings are quite weak in terms of coding power [Reference Richter24]. However, if one turns to non-effective notions such as Scott rank and Scott sentence complexity, the situation becomes less clear. It is not at all difficult to produce linear orderings of Scott rank
$\omega $
in its isomorphism type, shows that linear orderings are quite weak in terms of coding power [Reference Richter24]. However, if one turns to non-effective notions such as Scott rank and Scott sentence complexity, the situation becomes less clear. It is not at all difficult to produce linear orderings of Scott rank
![]() $\alpha $
for
$\alpha $
for
![]() $\alpha $
any countable ordinal; in fact Ash shows that one can find such examples by considering well-orderings [Reference Ash5]. Even among computable linear orderings one can find every possible Scott rank; Harrison [Reference Harrison15] and recently Calvert, Goncharov, and Knight [Reference Calvert, Goncharov and Knight7] exhibited computable linear orderings of Scott rank
$\alpha $
any countable ordinal; in fact Ash shows that one can find such examples by considering well-orderings [Reference Ash5]. Even among computable linear orderings one can find every possible Scott rank; Harrison [Reference Harrison15] and recently Calvert, Goncharov, and Knight [Reference Calvert, Goncharov and Knight7] exhibited computable linear orderings of Scott rank
![]() $\omega _{1}^{\mathrm {CK}}+1$
and
$\omega _{1}^{\mathrm {CK}}+1$
and
![]() $\omega _{1}^{\mathrm {CK}}$
, respectively. For the more fine-grained invariant of Scott sentence complexity, the possible Scott sentence complexities of computable structures with Scott rank
$\omega _{1}^{\mathrm {CK}}$
, respectively. For the more fine-grained invariant of Scott sentence complexity, the possible Scott sentence complexities of computable structures with Scott rank
![]() $\omega _{1}^{\mathrm {CK}}+1$
or
$\omega _{1}^{\mathrm {CK}}+1$
or
![]() $\omega _{1}^{\mathrm {CK}}$
were recently characterized in [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1] but the examples given were not linear orderings. This beckons the question whether there are linear orderings of all possible high Scott sentence complexities.
$\omega _{1}^{\mathrm {CK}}$
were recently characterized in [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1] but the examples given were not linear orderings. This beckons the question whether there are linear orderings of all possible high Scott sentence complexities.
There are two approaches one might consider to study the possible Scott sentence complexities in a specific class of structures. One is to study existing Borel reductions, such as the Friedman–Stanley embedding [Reference Friedman and Stanley8] and whether this embedding preserves Scott sentence complexities. We show that this approach fails in Section 2: The Friedman–Stanley embedding does not preserve Scott sentence complexity. In fact, for
![]() $\alpha>\omega $
, if
$\alpha>\omega $
, if
![]() $SSC(\mathcal {A})=\Sigma ^{\mathrm {in}}_{\alpha }$
, then,
$SSC(\mathcal {A})=\Sigma ^{\mathrm {in}}_{\alpha }$
, then,
![]() $SSC(FS(\mathcal {A}))=\Pi ^{\mathrm {in}}_{\alpha +1}$
(This is true for finite
$SSC(FS(\mathcal {A}))=\Pi ^{\mathrm {in}}_{\alpha +1}$
(This is true for finite
![]() $\alpha $
modulo a constant). The picture is different if
$\alpha $
modulo a constant). The picture is different if
![]() $SSC(\mathcal {A})=\Pi ^{\mathrm {in}}_{\alpha }$
: Then
$SSC(\mathcal {A})=\Pi ^{\mathrm {in}}_{\alpha }$
: Then
![]() $SSC(FS(\mathcal {A}))=\Pi ^{\mathrm {in}}_{\alpha }$
even in the case when
$SSC(FS(\mathcal {A}))=\Pi ^{\mathrm {in}}_{\alpha }$
even in the case when
![]() $\alpha $
is a limit ordinal (again modulo a constant if
$\alpha $
is a limit ordinal (again modulo a constant if
![]() $\alpha $
is finite). These results involve a deep analysis on the effect of parameters on the tree of tuples of a structure and a novel characterization of structures with Scott sentence complexity
$\alpha $
is finite). These results involve a deep analysis on the effect of parameters on the tree of tuples of a structure and a novel characterization of structures with Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
for
$\Pi ^{\mathrm {in}}_{\lambda }$
for
![]() $\lambda $
a limit ordinal using what we call unstable
$\lambda $
a limit ordinal using what we call unstable
![]() $\lambda $
-sequences.
$\lambda $
-sequences.
In Section 3 we show that our choice to study the Friedman–Stanley embedding was not arbitrary; there are no better Borel embeddings into the class of linear orderings in terms of preservation of Scott sentence complexity. In order to show this, we develop a concept we call
![]() $\alpha $
-universality. This tool provides upper bounds for the number of structures with particular Scott sentence complexities.
$\alpha $
-universality. This tool provides upper bounds for the number of structures with particular Scott sentence complexities.
In Sections 3.1 and 4 we take another more direct approach and try to find examples of linear orderings of given Scott sentence complexities. A summary of our findings can be found in the table above.
Table 2 Scott sentence complexities of linear orderings. Complexities not in the table are impossible for structures in general.

1.1 Remarks on effectivity
While this article’s primary concern is not the effectiveness of the presented results, many of our results in this article can be effectivized without much effort. The interested reader can find further discussions on this matter in subsections at the end of Sections 2 and 4. Included are comments on potential difficulties and open questions that arise from these efforts.
1.2 Preliminaries
We assume that the reader is familiar with the basic techniques of Scott analysis and with linear orderings in general. For background we refer to Montalbán’s upcoming book [Reference Montalbán22] and the standard reference by Ash and Knight [Reference Ash and Knight4].
We will make particular use of the following definition and lemma that are used regularly in Scott analysis.
Definition 1.1 [Reference Ash and Knight4, Section 17.4].
We say that a tuple is
![]() $\alpha $
-free in the structure
$\alpha $
-free in the structure
![]() $\mathcal {A}$
if for every tuple
$\mathcal {A}$
if for every tuple
![]() $\bar b\in A$
and every
$\bar b\in A$
and every
![]() $\beta <\alpha $
, there are tuples
$\beta <\alpha $
, there are tuples
![]() $\bar a',\bar b'$
such that
$\bar a',\bar b'$
such that
Lemma 1.2 [Reference Montalbán19].
The unparameterized Scott rank of a structure is the least
![]() $\alpha $
such that no tuple is
$\alpha $
such that no tuple is
![]() $\alpha $
-free.
$\alpha $
-free.
Let us highlight the following lemmas concerning linear orderings which we will use as basic tools in our proofs without reference.
Lemma 1.3 [Reference Ash and Knight4, Lemma 15.7].
Suppose
![]() $\mathcal {A},\mathcal {B}\in \mathrm {LO}$
,
$\mathcal {A},\mathcal {B}\in \mathrm {LO}$
,
![]() $\bar a\in \mathcal {A}^n$
and
$\bar a\in \mathcal {A}^n$
and
![]() $\bar b\in \mathcal {B}^n$
with
$\bar b\in \mathcal {B}^n$
with
![]() $\bar a$
and
$\bar a$
and
![]() $\bar b$
ordered. Then for every
$\bar b$
ordered. Then for every
![]() $\alpha <\omega _1$
$\alpha <\omega _1$
 $$\begin{align*}\begin{aligned} (\mathcal{A},\bar a)\leq_\alpha (\mathcal{B},\bar b) \iff (-\infty, a_{0})\leq_\alpha (-\infty, a_1) \land (a_0,a_1)\leq_\alpha (b_0,b_1) \land \\ \dots \land (a_{n-1},\infty)\leq_\alpha (b_{n-1},\infty).\end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} (\mathcal{A},\bar a)\leq_\alpha (\mathcal{B},\bar b) \iff (-\infty, a_{0})\leq_\alpha (-\infty, a_1) \land (a_0,a_1)\leq_\alpha (b_0,b_1) \land \\ \dots \land (a_{n-1},\infty)\leq_\alpha (b_{n-1},\infty).\end{aligned} \end{align*}$$
Lemma 1.4 [Reference Ash and Knight4, Lemma 15.8].
Suppose
![]() $\mathcal {A},\mathcal {B}\in \mathrm {LO}$
. Then
$\mathcal {A},\mathcal {B}\in \mathrm {LO}$
. Then
![]() $\mathcal {A}\leq _1 \mathcal {B}$
if and only if
$\mathcal {A}\leq _1 \mathcal {B}$
if and only if
![]() $\mathcal {A}$
is infinite or at least as large as
$\mathcal {A}$
is infinite or at least as large as
![]() $\mathcal {B}$
. For
$\mathcal {B}$
. For
![]() $\alpha>1$
,
$\alpha>1$
,
![]() $\mathcal {A}\leq _\alpha \mathcal {B}$
if and only if for every
$\mathcal {A}\leq _\alpha \mathcal {B}$
if and only if for every
![]() $1\leq \beta <\alpha $
and every partition of
$1\leq \beta <\alpha $
and every partition of
![]() $\mathcal {B}$
into intervals
$\mathcal {B}$
into intervals
![]() $\mathcal {B}_0,\dots ,\mathcal {B}_n$
, with endpoints in
$\mathcal {B}_0,\dots ,\mathcal {B}_n$
, with endpoints in
![]() $\mathcal {B}$
, there is a partition of
$\mathcal {B}$
, there is a partition of
![]() $\mathcal {A}$
into intervals
$\mathcal {A}$
into intervals
![]() $\mathcal {A}_1,\dots ,\mathcal {A}_n$
with endpoints in
$\mathcal {A}_1,\dots ,\mathcal {A}_n$
with endpoints in
![]() $\mathcal {A}$
, such that
$\mathcal {A}$
, such that
![]() $\mathcal {B}_i\leq _\beta \mathcal {A}_i$
.
$\mathcal {B}_i\leq _\beta \mathcal {A}_i$
.
2 The Friedman–Stanley embedding and Scott sentence complexity
Friedman and Stanley [Reference Friedman and Stanley8] showed that the class of linear orderings is Borel complete by defining a computable operator
![]() $\Phi $
that takes a structure in a fixed vocabulary as input and outputs a linear ordering such that for all
$\Phi $
that takes a structure in a fixed vocabulary as input and outputs a linear ordering such that for all
![]() $\mathcal {A},\mathcal {B}$
,
$\mathcal {A},\mathcal {B}$
,
![]() $\mathcal {A}\cong \mathcal {B}$
if and only if
$\mathcal {A}\cong \mathcal {B}$
if and only if
![]() $\Phi (\mathcal {A})\cong \Phi (\mathcal {B})$
. This reduction is commonly referred to as the Friedman–Stanley embedding. It proceeds in two steps:
$\Phi (\mathcal {A})\cong \Phi (\mathcal {B})$
. This reduction is commonly referred to as the Friedman–Stanley embedding. It proceeds in two steps:
-
(1) Given a structure
 $\mathcal {A}$
it produces a labeled tree
$\mathcal {A}$
it produces a labeled tree
 ${\mathcal {T}}_{\mathcal {A}}$
, the tree of tuples of
${\mathcal {T}}_{\mathcal {A}}$
, the tree of tuples of
 $\mathcal {A}$
.
$\mathcal {A}$
. -
(2) From
 ${\mathcal {T}}_{\mathcal {A}}$
it produces a linear ordering
${\mathcal {T}}_{\mathcal {A}}$
it produces a linear ordering
 $L_{\mathcal {A}}=\Phi (\mathcal {A})$
.
$L_{\mathcal {A}}=\Phi (\mathcal {A})$
.
The Friedman–Stanley embedding has been heavily studied both by descriptive set theorists and computable structure theorists. Closely connected to our investigation are Harrison-Trainor and Montalbán’s study of the tree of tuples construction [Reference Harrison-Trainor and Montalbán16] and Knight, Soskova, and Vatev’s analysis of possible reductions to linear orderings [Reference Knight, Soskova and Vatev17]. One result obtained in both articles is that one cannot embed graphs into linear orderings uniformly using
![]() $L_{\omega _1\omega }$
formulas. This raises the question whether the Friedman–Stanley embedding or any reduction reducing graphs to linear orderings can preserve Scott sentence complexity. We consider the first question in this section by analyzing the two steps of the reduction.
$L_{\omega _1\omega }$
formulas. This raises the question whether the Friedman–Stanley embedding or any reduction reducing graphs to linear orderings can preserve Scott sentence complexity. We consider the first question in this section by analyzing the two steps of the reduction.
Using the fact that the class of graphs is complete for very strong reducibilities such as effective bi-interpretability (see [Reference Montalbán21]), we will only analyse the Friedman–Stanley embedding from the vocabulary containing one binary relation symbol to linear orderings. This has the advantage that we do not have to deal with technicalities resulting from infinite vocabularies in our proofs, but there is no effect on the strength of our results.
2.1 The tree of tuples and Scott sentence complexity
Definition 2.1. A replicated labeled tree consists of a tree
![]() $(T,\succeq )$
with a parent function and labeling function
$(T,\succeq )$
with a parent function and labeling function
![]() $l:T\to \omega $
such that for every
$l:T\to \omega $
such that for every
![]() $\sigma \in T$
with parent
$\sigma \in T$
with parent
![]() $\tau $
, there exist infinitely many children
$\tau $
, there exist infinitely many children
![]() $\tilde \sigma $
of
$\tilde \sigma $
of
![]() $\tau $
such that
$\tau $
such that
![]() ${\mathcal {T}}_\sigma \cong {\mathcal {T}}_{\tilde \sigma }$
, where
${\mathcal {T}}_\sigma \cong {\mathcal {T}}_{\tilde \sigma }$
, where
![]() ${\mathcal {T}}_\sigma $
denotes the subtree of
${\mathcal {T}}_\sigma $
denotes the subtree of
![]() ${\mathcal {T}}_{\mathcal {A}}$
rooted at
${\mathcal {T}}_{\mathcal {A}}$
rooted at
![]() $\sigma $
.
$\sigma $
.
Recall that the atomic diagram of a tuple
![]() $\bar a$
in
$\bar a$
in
![]() $\mathcal {A}$
, denoted by
$\mathcal {A}$
, denoted by
![]() $D_{\mathcal {A}}(\bar a)$
is the set of atomic formulas
$D_{\mathcal {A}}(\bar a)$
is the set of atomic formulas
![]() $\varphi _i$
in variables
$\varphi _i$
in variables
![]() $(x_i)_{i\in \omega }$
such that
$(x_i)_{i\in \omega }$
such that
![]() $(\mathcal {A},\bar a)\models \varphi _i[x_j/a_j, j<|\bar a|]$
. We use the convention that formulas mentioning variables
$(\mathcal {A},\bar a)\models \varphi _i[x_j/a_j, j<|\bar a|]$
. We use the convention that formulas mentioning variables
![]() $x_j$
with
$x_j$
with
![]() $j\geq |\bar a|$
are not in
$j\geq |\bar a|$
are not in
![]() $D_{\mathcal {A}}(\bar a)$
and thus, assuming that
$D_{\mathcal {A}}(\bar a)$
and thus, assuming that
![]() $\mathcal {A}$
is a graph,
$\mathcal {A}$
is a graph,
![]() $D_{\mathcal {A}}(\bar a)$
will always be a finite set.
$D_{\mathcal {A}}(\bar a)$
will always be a finite set.
Definition 2.2. Given a graph
![]() $\mathcal {A}$
let
$\mathcal {A}$
let
![]() $T_{\mathcal {A}}$
be the labeled tree consisting of all tuples from
$T_{\mathcal {A}}$
be the labeled tree consisting of all tuples from
![]() $\mathcal {A}$
ordered by inclusion where each tuple
$\mathcal {A}$
ordered by inclusion where each tuple
![]() $\bar a$
is labeled by a natural number coding
$\bar a$
is labeled by a natural number coding
![]() $D_{\mathcal {A}}(\bar a)$
and the length of
$D_{\mathcal {A}}(\bar a)$
and the length of
![]() $\bar a$
. The tree of tuples
$\bar a$
. The tree of tuples
![]() ${\mathcal {T}}_{\mathcal {A}}$
is obtained by replicating every branch in
${\mathcal {T}}_{\mathcal {A}}$
is obtained by replicating every branch in
![]() $T_{\mathcal {A}}$
infinitely many times.
$T_{\mathcal {A}}$
infinitely many times.
Looking at the construction of
![]() ${\mathcal {T}}_{\mathcal {A}}$
we can see that the Friedman–Stanley embedding does not preserve much structure. Suppose that
${\mathcal {T}}_{\mathcal {A}}$
we can see that the Friedman–Stanley embedding does not preserve much structure. Suppose that
![]() $\mathcal {A}$
is rigid (i.e., it has trivial automorphism group). The tree
$\mathcal {A}$
is rigid (i.e., it has trivial automorphism group). The tree
![]() ${\mathcal {T}}_{\mathcal {A}}$
will have many automorphisms because it is replicated, and thus the automorphism groups of
${\mathcal {T}}_{\mathcal {A}}$
will have many automorphisms because it is replicated, and thus the automorphism groups of
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() ${\mathcal {T}}_{\mathcal {A}}$
will behave quite differently.
${\mathcal {T}}_{\mathcal {A}}$
will behave quite differently.
On the other hand, the (unparameterized) Scott rank of the tree of tuples of a structure and the Scott rank of the structure are equal. In order to show this we need a few lemmas.
Lemma 2.3. Let
![]() $\mathcal {A}$
be a structure in vocabulary
$\mathcal {A}$
be a structure in vocabulary
![]() $\tau $
.
$\tau $
.
-
(1) Given
 $\Pi ^{\mathrm {in}}_{\alpha }$
$\Pi ^{\mathrm {in}}_{\alpha }$
 $\tau $
-formula
$\tau $
-formula
 $\varphi $
, there is a
$\varphi $
, there is a
 $\Pi ^{\mathrm {in}}_{\alpha }$
formula
$\Pi ^{\mathrm {in}}_{\alpha }$
formula
 $T_\varphi $
in the vocabulary of labeled trees such that for any
$T_\varphi $
in the vocabulary of labeled trees such that for any
 $\bar a\in \mathcal {A}$
and every
$\bar a\in \mathcal {A}$
and every
 $\sigma \in {\mathcal {T}}_{\mathcal {A}}$
with
$\sigma \in {\mathcal {T}}_{\mathcal {A}}$
with
 $\sigma \succeq \bar a$
Moreover,
$\sigma \succeq \bar a$
Moreover, $$\begin{align*}\mathcal{A}\models\varphi(\bar a)\iff {\mathcal{T}}_{\mathcal{A}}\models T_\varphi(\sigma).\end{align*}$$
$$\begin{align*}\mathcal{A}\models\varphi(\bar a)\iff {\mathcal{T}}_{\mathcal{A}}\models T_\varphi(\sigma).\end{align*}$$
 $T_\varphi $
can be taken to have the same quantifier complexity as
$T_\varphi $
can be taken to have the same quantifier complexity as
 $\varphi $
.
$\varphi $
.
-
(2) Given a
 $\Pi ^{\mathrm {in}}_{\alpha }$
formula
$\Pi ^{\mathrm {in}}_{\alpha }$
formula
 $\psi $
in the vocabulary of labeled trees, there is a
$\psi $
in the vocabulary of labeled trees, there is a
 $\Pi ^{\mathrm {in}}_{\alpha }$
$\Pi ^{\mathrm {in}}_{\alpha }$
 $\tau $
-formula
$\tau $
-formula
 $\psi ^*$
such that for any tuple
$\psi ^*$
such that for any tuple
 $\bar {\sigma }=(\bar a_1,\dots ,\bar a_n)\in {\mathcal {T}}_{\mathcal {A}}$
$\bar {\sigma }=(\bar a_1,\dots ,\bar a_n)\in {\mathcal {T}}_{\mathcal {A}}$
 $$\begin{align*}{\mathcal{T}}_{\mathcal{A}}\models \psi(\bar{\sigma}) \iff \mathcal{A}\models\psi^*(\bar a,\dots,\bar a_n).\end{align*}$$
$$\begin{align*}{\mathcal{T}}_{\mathcal{A}}\models \psi(\bar{\sigma}) \iff \mathcal{A}\models\psi^*(\bar a,\dots,\bar a_n).\end{align*}$$
Proof. We start by proving Item 1. To start suppose that
![]() $\varphi $
is finite and quantifier-free and in disjunctive normal form. For a disjunct
$\varphi $
is finite and quantifier-free and in disjunctive normal form. For a disjunct
![]() $\varphi _i$
of
$\varphi _i$
of
![]() $\varphi $
, let
$\varphi $
, let
![]() $T_{\varphi _i}$
be the formula expressing that
$T_{\varphi _i}$
be the formula expressing that
![]() $\varphi _i\subseteq l(x)$
and let
$\varphi _i\subseteq l(x)$
and let
![]() $T_\varphi =\bigvee T_{\varphi _i}$
. Since formulas with free variable indices exceeding the length of a tuple
$T_\varphi =\bigvee T_{\varphi _i}$
. Since formulas with free variable indices exceeding the length of a tuple
![]() $\bar a$
are considered to be false in
$\bar a$
are considered to be false in
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $l(\sigma )\subseteq l(\tau )$
if
$l(\sigma )\subseteq l(\tau )$
if
![]() $\sigma \preceq \tau $
, we have that
$\sigma \preceq \tau $
, we have that
![]() $\mathcal {A}\models \varphi (\bar a)$
if and only if for every
$\mathcal {A}\models \varphi (\bar a)$
if and only if for every
![]() $\sigma \succeq \bar a$
,
$\sigma \succeq \bar a$
,
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_\varphi (\sigma )$
, as required.
${\mathcal {T}}_{\mathcal {A}}\models T_\varphi (\sigma )$
, as required.
Now, say that we have defined
![]() $T_\varphi $
given
$T_\varphi $
given
![]() $\varphi $
and that Item 1 holds for
$\varphi $
and that Item 1 holds for
![]() $\varphi (x)$
. Define
$\varphi (x)$
. Define

where
![]() $\varphi [x/x_i]$
denotes
$\varphi [x/x_i]$
denotes
![]() $\varphi $
with all free occurrences of x replaced by
$\varphi $
with all free occurrences of x replaced by
![]() $x_i$
. The need for these replacements arises from our coding: We have that
$x_i$
. The need for these replacements arises from our coding: We have that
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
in
$\tau $
in
![]() ${\mathcal {T}}_{\mathcal {A}}$
can code a witness a for x in different positions, say for example that
${\mathcal {T}}_{\mathcal {A}}$
can code a witness a for x in different positions, say for example that
![]() $\sigma (i)=\tau (k)=a$
for
$\sigma (i)=\tau (k)=a$
for
![]() $i\neq k$
. Then
$i\neq k$
. Then
![]() $\sigma $
satisfies
$\sigma $
satisfies
![]() $T_{\varphi [x/x_i]}$
but
$T_{\varphi [x/x_i]}$
but
![]() $\tau $
does not. To proceed we will need the following claim.
$\tau $
does not. To proceed we will need the following claim.
Claim 1.3.1. Suppose that
![]() $\varphi $
is a formula where exactly one free variable x is not in the range
$\varphi $
is a formula where exactly one free variable x is not in the range
![]() $x_0,\dots , x_{|a|}$
. Then for all b and
$x_0,\dots , x_{|a|}$
. Then for all b and
![]() $\bar d$
not containing b
$\bar d$
not containing b
Proof. First note that if
![]() $\sigma =\pi (\tau )$
where
$\sigma =\pi (\tau )$
where
![]() $\pi $
is a permutation of
$\pi $
is a permutation of
![]() $|\sigma |$
, then for any formula
$|\sigma |$
, then for any formula
![]() $T_\varphi $
,
$T_\varphi $
,
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_\varphi (\sigma )$
if and only if
${\mathcal {T}}_{\mathcal {A}}\models T_\varphi (\sigma )$
if and only if
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_\varphi [x_i/x_{\pi (i)}](\tau )$
.Footnote
1
${\mathcal {T}}_{\mathcal {A}}\models T_\varphi [x_i/x_{\pi (i)}](\tau )$
.Footnote
1
Now, suppose that
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi {[x/x_{|\bar a^{\smallfrown } \bar d|+1}]}}(\bar a^{\smallfrown } \bar d^{\smallfrown } b)$
, then as
${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi {[x/x_{|\bar a^{\smallfrown } \bar d|+1}]}}(\bar a^{\smallfrown } \bar d^{\smallfrown } b)$
, then as
![]() $T_\varphi $
does not contain variable symbols
$T_\varphi $
does not contain variable symbols
![]() $x_i$
for
$x_i$
for
![]() $i>|\bar a|$
except x,
$i>|\bar a|$
except x,
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi {[x/x_{|\bar a|+1}]}}(\bar a^{\smallfrown } b^{\smallfrown } \bar d)$
and in particular
${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi {[x/x_{|\bar a|+1}]}}(\bar a^{\smallfrown } b^{\smallfrown } \bar d)$
and in particular
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi {[ x/x_{|\bar a|+1} ]}}(\bar a^{\smallfrown } b)$
. The other implication is trivial.
${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi {[ x/x_{|\bar a|+1} ]}}(\bar a^{\smallfrown } b)$
. The other implication is trivial.
We can now proceed with the induction step of Item 1. We have by the claim that for given
![]() $\bar a$
and b,
$\bar a$
and b,
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_\varphi (\bar a^{\smallfrown } b)$
if and only if for every
${\mathcal {T}}_{\mathcal {A}}\models T_\varphi (\bar a^{\smallfrown } b)$
if and only if for every
![]() $\sigma \succeq \bar a$
,
$\sigma \succeq \bar a$
,
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi [x/x_{|\sigma |+1}]} (\sigma ^{\smallfrown } b)$
if
${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi [x/x_{|\sigma |+1}]} (\sigma ^{\smallfrown } b)$
if
![]() $b\not \in \sigma $
and
$b\not \in \sigma $
and
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi [x/x_i]}(\sigma )$
if
${\mathcal {T}}_{\mathcal {A}}\models T_{\varphi [x/x_i]}(\sigma )$
if
![]() $b=\sigma (i)$
. Thus, we get that
$b=\sigma (i)$
. Thus, we get that
![]() $\mathcal {A}\models \exists x\varphi (\bar a)$
if and only if for every
$\mathcal {A}\models \exists x\varphi (\bar a)$
if and only if for every
![]() $\sigma \succeq \bar a$
,
$\sigma \succeq \bar a$
,
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_{\exists x\varphi }(\sigma )$
. For
${\mathcal {T}}_{\mathcal {A}}\models T_{\exists x\varphi }(\sigma )$
. For
![]() $T_{\forall x\varphi }$
note that
$T_{\forall x\varphi }$
note that
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_{\forall x \varphi }(\bar a)$
if and only if for every
${\mathcal {T}}_{\mathcal {A}}\models T_{\forall x \varphi }(\bar a)$
if and only if for every
![]() $\sigma \succeq \bar a$
and every
$\sigma \succeq \bar a$
and every
![]() $i\leq |\sigma |$
,
$i\leq |\sigma |$
,
![]() $\mathcal {A}\models \varphi (\bar a,\sigma (i))$
, and, since
$\mathcal {A}\models \varphi (\bar a,\sigma (i))$
, and, since
![]() $\bar a=\sigma \operatorname {\mathrm {\upharpoonright }} |\bar a|$
, in particular
$\bar a=\sigma \operatorname {\mathrm {\upharpoonright }} |\bar a|$
, in particular
![]() $\mathcal {A}\models \varphi (\sigma (0)\dots \sigma (|\bar a|),\sigma (i))$
. Thus,
$\mathcal {A}\models \varphi (\sigma (0)\dots \sigma (|\bar a|),\sigma (i))$
. Thus,
![]() $\mathcal {A}\models \forall x \varphi (\bar a)$
if and only if
$\mathcal {A}\models \forall x \varphi (\bar a)$
if and only if
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_{\forall x \varphi }$
. We can extend our definitions to include infinite conjunctions and disjunctions by letting
${\mathcal {T}}_{\mathcal {A}}\models T_{\forall x \varphi }$
. We can extend our definitions to include infinite conjunctions and disjunctions by letting
It then follows that for every
![]() $\bar a$
,
$\bar a$
,
![]() $\mathcal {A}\models \varphi (\bar a)$
if and only if
$\mathcal {A}\models \varphi (\bar a)$
if and only if
![]() $T_{\mathcal {A}}\models T_\varphi (\sigma )$
for all
$T_{\mathcal {A}}\models T_\varphi (\sigma )$
for all
![]() $\sigma \succeq \bar a$
, and, by construction
$\sigma \succeq \bar a$
, and, by construction
![]() $T_\varphi $
has the same quantifier complexity as
$T_\varphi $
has the same quantifier complexity as
![]() $\varphi $
.
$\varphi $
.
We now prove Item 2 by defining for each
![]() $\bar \sigma =(\bar a_1,\dots ,\bar a_n)\in {\mathcal {T}}_{\mathcal {A}}$
a Turing-computable embedding from the isomorphism class of
$\bar \sigma =(\bar a_1,\dots ,\bar a_n)\in {\mathcal {T}}_{\mathcal {A}}$
a Turing-computable embedding from the isomorphism class of
![]() $\mathcal {A}$
in the extended vocabulary with additional constant symbols
$\mathcal {A}$
in the extended vocabulary with additional constant symbols
![]() $\bar p=\bar p_1\dots ,\bar p_n$
such that
$\bar p=\bar p_1\dots ,\bar p_n$
such that
![]() $|\bar p_i|=|\bar a_i|$
to the class of trees with constant symbols for
$|\bar p_i|=|\bar a_i|$
to the class of trees with constant symbols for
![]() $\sigma $
. That is, the embedding
$\sigma $
. That is, the embedding
![]() $\Phi _\sigma $
will map
$\Phi _\sigma $
will map
![]() $Iso(\mathcal {A},\bar p)$
to
$Iso(\mathcal {A},\bar p)$
to
![]() $Iso({\mathcal {T}}_{\mathcal {A}},\bar \tau )$
, where
$Iso({\mathcal {T}}_{\mathcal {A}},\bar \tau )$
, where
![]() $\tau _i=\bar p_i$
for all
$\tau _i=\bar p_i$
for all
![]() $i<n$
and
$i<n$
and
![]() $\bar p_i\in A^{<\omega }$
. Each of these embeddings will extend the Friedman–Stanley embedding that acts without parameters.
$\bar p_i\in A^{<\omega }$
. Each of these embeddings will extend the Friedman–Stanley embedding that acts without parameters.
Fix
![]() $\sigma =(\bar a_1,\dots ,\bar a_n)\in {\mathcal {T}}_{\mathcal {A}}$
and consider a structure
$\sigma =(\bar a_1,\dots ,\bar a_n)\in {\mathcal {T}}_{\mathcal {A}}$
and consider a structure
![]() $(\mathcal {B},\bar p)$
in the extended vocabulary such that
$(\mathcal {B},\bar p)$
in the extended vocabulary such that
![]() $\mathcal {B}\cong \mathcal {A}$
. The Turing computable embedding
$\mathcal {B}\cong \mathcal {A}$
. The Turing computable embedding
![]() $\Phi _\sigma $
computes the standard tree of structures for
$\Phi _\sigma $
computes the standard tree of structures for
![]() $\mathcal {B}$
and picks the lexicographically least tuple
$\mathcal {B}$
and picks the lexicographically least tuple
![]() $\bar \tau $
from
$\bar \tau $
from
![]() ${\mathcal {T}}_{\mathcal {B}}$
such that each
${\mathcal {T}}_{\mathcal {B}}$
such that each
![]() $\tau _i$
codes
$\tau _i$
codes
![]() $\bar p_i$
and the finite subtree described by
$\bar p_i$
and the finite subtree described by
![]() $\bar \tau $
in
$\bar \tau $
in
![]() ${\mathcal {T}}_{\mathcal {B}}$
is isomorphic to the finite subtree described by
${\mathcal {T}}_{\mathcal {B}}$
is isomorphic to the finite subtree described by
![]() $\bar \sigma $
(notice that this last condition is necessary since
$\bar \sigma $
(notice that this last condition is necessary since
![]() ${\mathcal {T}}_{\mathcal {A}}$
is replicated. While
${\mathcal {T}}_{\mathcal {A}}$
is replicated. While
![]() $\bar a_i$
and
$\bar a_i$
and
![]() $\bar a_j$
could agree on an initial segment, it could happen that the subtrees generated by the elements coding these tuples in
$\bar a_j$
could agree on an initial segment, it could happen that the subtrees generated by the elements coding these tuples in
![]() ${\mathcal {T}}_{\mathcal {A}}$
are disjoint). It is not difficult to check that
${\mathcal {T}}_{\mathcal {A}}$
are disjoint). It is not difficult to check that
![]() $\Phi _\sigma : (\mathcal {B},\bar p) \mapsto ({\mathcal {T}}_{\mathcal {B}},\bar \tau )$
is a Turing computable embedding mapping
$\Phi _\sigma : (\mathcal {B},\bar p) \mapsto ({\mathcal {T}}_{\mathcal {B}},\bar \tau )$
is a Turing computable embedding mapping
![]() $(\mathcal {A},\bar a_1,\dots ,\bar a_n)$
to
$(\mathcal {A},\bar a_1,\dots ,\bar a_n)$
to
![]() $({\mathcal {T}}_{\mathcal {A}},\bar {\sigma })$
. Now, for any formula
$({\mathcal {T}}_{\mathcal {A}},\bar {\sigma })$
. Now, for any formula
![]() $\psi $
in the language of labeled trees and parameters
$\psi $
in the language of labeled trees and parameters
![]() $\sigma =(\bar a_1,\dots ,\bar a_n)$
by the pull-back theorem for
$\sigma =(\bar a_1,\dots ,\bar a_n)$
by the pull-back theorem for
![]() $\Psi _{\bar {\sigma }}$
there is
$\Psi _{\bar {\sigma }}$
there is
![]() $\psi ^*$
of the same complexity as
$\psi ^*$
of the same complexity as
![]() $\psi $
such that
$\psi $
such that
![]() $\mathcal {A}\models \psi ^*(\bar a_1\dots \bar a_n)$
if and only if
$\mathcal {A}\models \psi ^*(\bar a_1\dots \bar a_n)$
if and only if
![]() ${\mathcal {T}}_{\mathcal {A}}\models \psi (\bar {\sigma })$
. This proves Item 2.
${\mathcal {T}}_{\mathcal {A}}\models \psi (\bar {\sigma })$
. This proves Item 2.
Lemma 2.3 might suggest that the tree of tuples reduction preserves Scott sentence complexity. However, as we will see, it does not. The reason for this is the following. Let K be a class of structures and look at
![]() $T(K)$
, the set of trees-of-tuples of the elements of K, then within
$T(K)$
, the set of trees-of-tuples of the elements of K, then within
![]() $T(K)$
, Scott sentences are preserved. However, in general
$T(K)$
, Scott sentences are preserved. However, in general
![]() $T(K)$
is not a Borel subset of the class of labeled trees and thus the Scott sentence complexity of
$T(K)$
is not a Borel subset of the class of labeled trees and thus the Scott sentence complexity of
![]() ${\mathcal {T}}_{\mathcal {A}}$
is not a priori connected to the Scott sentence complexity of
${\mathcal {T}}_{\mathcal {A}}$
is not a priori connected to the Scott sentence complexity of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proposition 2.4. Given
![]() $\bar {\sigma }=(\bar a_1,\dots ,\bar a_n),\bar \tau =(\bar b_1,\dots ,\bar b_n)\in {\mathcal {T}}_{\mathcal {A}}$
, if
$\bar {\sigma }=(\bar a_1,\dots ,\bar a_n),\bar \tau =(\bar b_1,\dots ,\bar b_n)\in {\mathcal {T}}_{\mathcal {A}}$
, if
![]() $\bar {\sigma }\leq _\alpha \bar \tau $
, then for each
$\bar {\sigma }\leq _\alpha \bar \tau $
, then for each
![]() $i<n$
,
$i<n$
,
![]() $\bar a_i\leq _\alpha \bar b_i$
.
$\bar a_i\leq _\alpha \bar b_i$
.
Proof. We prove this by contraposition. Assume that for some i,
![]() $\bar a_i\not \leq _\alpha \bar b_i$
. This is the same thing as saying that there is a
$\bar a_i\not \leq _\alpha \bar b_i$
. This is the same thing as saying that there is a
![]() $\Pi ^{\mathrm {in}}_{\alpha }$
formula
$\Pi ^{\mathrm {in}}_{\alpha }$
formula
![]() $\varphi $
with
$\varphi $
with
![]() $\mathcal {A}\models \varphi (\bar a_i)$
and
$\mathcal {A}\models \varphi (\bar a_i)$
and
![]() $\mathcal {A}\models \lnot \varphi (\bar b_i)$
. From Item 1 of Lemma 2.3 we get that
$\mathcal {A}\models \lnot \varphi (\bar b_i)$
. From Item 1 of Lemma 2.3 we get that
![]() ${\mathcal {T}}_{\mathcal {A}}\models T_\varphi (\bar a_i)$
and
${\mathcal {T}}_{\mathcal {A}}\models T_\varphi (\bar a_i)$
and
![]() ${\mathcal {T}}_{\mathcal {A}}\models \lnot T_\varphi (\bar b_i)$
. Then, since
${\mathcal {T}}_{\mathcal {A}}\models \lnot T_\varphi (\bar b_i)$
. Then, since
![]() $T_\varphi $
is
$T_\varphi $
is
![]() $\Pi ^{\mathrm {in}}_{\alpha }$
,
$\Pi ^{\mathrm {in}}_{\alpha }$
,
![]() $\sigma \not \leq _\alpha \tau $
, as desired.
$\sigma \not \leq _\alpha \tau $
, as desired.
Lemma 2.5. Given a tree of tuples
![]() ${\mathcal {T}}_{\mathcal {A}}$
, an element
${\mathcal {T}}_{\mathcal {A}}$
, an element
![]() $\sigma \in {\mathcal {T}}_{\mathcal {A}}$
, and a set of finitely many children
$\sigma \in {\mathcal {T}}_{\mathcal {A}}$
, and a set of finitely many children
![]() $\tau _1,\dots ,\tau _n$
of
$\tau _1,\dots ,\tau _n$
of
![]() $\sigma $
,
$\sigma $
,
Proof. Since
![]() ${\mathcal {T}}_{\mathcal {A}}$
is replicated, for every child
${\mathcal {T}}_{\mathcal {A}}$
is replicated, for every child
![]() $\rho $
of
$\rho $
of
![]() $\sigma $
there are infinitely many children
$\sigma $
there are infinitely many children
![]() $\rho '$
of
$\rho '$
of
![]() $\sigma $
such that
$\sigma $
such that
![]() ${\mathcal {T}}_\rho '\cong {\mathcal {T}}_\rho $
. Hence,
${\mathcal {T}}_\rho '\cong {\mathcal {T}}_\rho $
. Hence,
![]() ${\mathcal {T}}_\sigma \cong {\mathcal {T}}_\sigma \setminus {\mathcal {T}}_\rho $
. The full lemma follows by a trivial induction.
${\mathcal {T}}_\sigma \cong {\mathcal {T}}_\sigma \setminus {\mathcal {T}}_\rho $
. The full lemma follows by a trivial induction.
Theorem 2.6. For any structure
![]() $\mathcal {A}$
,
$\mathcal {A}$
,
![]() $SR(\mathcal {A})=SR({\mathcal {T}}_{\mathcal {A}})$
.
$SR(\mathcal {A})=SR({\mathcal {T}}_{\mathcal {A}})$
.
Proof. Let
![]() $\mathcal {A}$
be a structure such that
$\mathcal {A}$
be a structure such that
![]() $SR({\mathcal {T}}_{\mathcal {A}})=\gamma $
. Consider a tuple
$SR({\mathcal {T}}_{\mathcal {A}})=\gamma $
. Consider a tuple
![]() $\bar a\in \mathcal {A}$
. Let
$\bar a\in \mathcal {A}$
. Let
![]() $\psi \in \Sigma ^{\mathrm {in}}_{\gamma }$
define the orbit of
$\psi \in \Sigma ^{\mathrm {in}}_{\gamma }$
define the orbit of
![]() $\bar a\in {\mathcal {T}}_{\mathcal {A}}$
. By Item 2 in Lemma 2.3 we have for all
$\bar a\in {\mathcal {T}}_{\mathcal {A}}$
. By Item 2 in Lemma 2.3 we have for all
![]() $\bar b\in \mathcal {A}$
$\bar b\in \mathcal {A}$
Therefore,
![]() $\psi ^*$
defines the orbit of
$\psi ^*$
defines the orbit of
![]() $\bar a$
as desired and hence,
$\bar a$
as desired and hence,
![]() $SR(\mathcal {A})\leq SR({\mathcal {T}}_{\mathcal {A}})$
.
$SR(\mathcal {A})\leq SR({\mathcal {T}}_{\mathcal {A}})$
.
We now show that
![]() $SR({\mathcal {T}}_{\mathcal {A}})\leq SR(\mathcal {A})=\gamma $
. Let
$SR({\mathcal {T}}_{\mathcal {A}})\leq SR(\mathcal {A})=\gamma $
. Let
![]() $\bar {\sigma }=\bar a_1\dots \bar a_n$
be a tuple in
$\bar {\sigma }=\bar a_1\dots \bar a_n$
be a tuple in
![]() ${\mathcal {T}}_{\mathcal {A}}$
. The automorphism orbit of each
${\mathcal {T}}_{\mathcal {A}}$
. The automorphism orbit of each
![]() $\bar a_i$
and each of its prefixes is
$\bar a_i$
and each of its prefixes is
![]() $\Sigma ^{\mathrm {in}}_{\gamma }$
definable in
$\Sigma ^{\mathrm {in}}_{\gamma }$
definable in
![]() $\mathcal {A}$
. Thus, by Item 1 in Lemma 2.3, for every k there is a
$\mathcal {A}$
. Thus, by Item 1 in Lemma 2.3, for every k there is a
![]() $\Sigma ^{\mathrm {in}}_{\gamma }$
formula,
$\Sigma ^{\mathrm {in}}_{\gamma }$
formula,
![]() $\chi _{i,k}$
, true only of elements in
$\chi _{i,k}$
, true only of elements in
![]() $\tau \in \mathcal {T}_{\mathcal {A}}$
where
$\tau \in \mathcal {T}_{\mathcal {A}}$
where
![]() $\tau $
codes a tuple with length k prefix automorphic to the length k prefix of
$\tau $
codes a tuple with length k prefix automorphic to the length k prefix of
![]() $\bar a_i$
. In particular,
$\bar a_i$
. In particular,
![]() $\mathcal {T}_{\tau \operatorname {\mathrm {\upharpoonright }} k}\cong \mathcal {T}_{\bar a_i\operatorname {\mathrm {\upharpoonright }} k}$
. Now, let
$\mathcal {T}_{\tau \operatorname {\mathrm {\upharpoonright }} k}\cong \mathcal {T}_{\bar a_i\operatorname {\mathrm {\upharpoonright }} k}$
. Now, let
![]() $\psi $
describe the finite subtree containing precisely the elements of
$\psi $
describe the finite subtree containing precisely the elements of
![]() $\sigma $
as its leaves and let
$\sigma $
as its leaves and let
![]() $\varphi $
be the conjunction of
$\varphi $
be the conjunction of
![]() $\psi $
together with the
$\psi $
together with the
![]() $\chi _{i,k}$
. Note that
$\chi _{i,k}$
. Note that
![]() $\varphi $
can be taken to have free variables corresponding to
$\varphi $
can be taken to have free variables corresponding to
![]() $\sigma $
. Because the labels encode the height of the labeled element in the tree,
$\sigma $
. Because the labels encode the height of the labeled element in the tree,
![]() $\psi $
can be taken
$\psi $
can be taken
![]() $\Sigma ^{\mathrm {in}}_{1}$
.
$\Sigma ^{\mathrm {in}}_{1}$
.
Let
![]() $\bar \tau =\bar b_1\dots \bar b_n$
satisfy
$\bar \tau =\bar b_1\dots \bar b_n$
satisfy
![]() $\varphi $
and consider the subtrees
$\varphi $
and consider the subtrees
![]() $\mathcal T_\sigma $
and
$\mathcal T_\sigma $
and
![]() $\mathcal T_\tau $
containing elements of
$\mathcal T_\tau $
containing elements of
![]() ${\mathcal {T}}_{\mathcal {A}}$
comparable with
${\mathcal {T}}_{\mathcal {A}}$
comparable with
![]() $\sigma $
, respectively
$\sigma $
, respectively
![]() $\tau $
. These two subtrees are isomorphic by Lemma 2.5 and as
$\tau $
. These two subtrees are isomorphic by Lemma 2.5 and as
![]() ${\mathcal {T}}_{\bar a_i\operatorname {\mathrm {\upharpoonright }} k}\cong {\mathcal {T}}_{\bar b_i\operatorname {\mathrm {\upharpoonright }} k}$
for all
${\mathcal {T}}_{\bar a_i\operatorname {\mathrm {\upharpoonright }} k}\cong {\mathcal {T}}_{\bar b_i\operatorname {\mathrm {\upharpoonright }} k}$
for all
![]() $i<n$
and
$i<n$
and
![]() $k<|\bar a_i|$
. Fix
$k<|\bar a_i|$
. Fix
![]() $h(\tau )$
such that
$h(\tau )$
such that
![]() ${\mathcal {T}}_\tau \cong {\mathcal {T}}_{h(\tau )}$
yet the tree
${\mathcal {T}}_\tau \cong {\mathcal {T}}_{h(\tau )}$
yet the tree
![]() ${\mathcal {T}}_{h(\tau )}$
is disjoint from both
${\mathcal {T}}_{h(\tau )}$
is disjoint from both
![]() ${\mathcal {T}}_\sigma $
and
${\mathcal {T}}_\sigma $
and
![]() ${\mathcal {T}}_\tau $
. Since
${\mathcal {T}}_\tau $
. Since
![]() ${\mathcal {T}}$
is replicated we can find such an
${\mathcal {T}}$
is replicated we can find such an
![]() $h(\tau )$
and furthermore find an automorphism h such that
$h(\tau )$
and furthermore find an automorphism h such that
![]() $\tau $
is switched with
$\tau $
is switched with
![]() $h(\tau )$
and all points outside of
$h(\tau )$
and all points outside of
![]() ${\mathcal {T}}_\tau $
and
${\mathcal {T}}_\tau $
and
![]() ${\mathcal {T}}_{h(\tau )}$
are fixed. Similarly, as
${\mathcal {T}}_{h(\tau )}$
are fixed. Similarly, as
![]() ${\mathcal {T}}_\sigma \cong {\mathcal {T}}_{h(\tau )}$
there is an automorphism f that switches
${\mathcal {T}}_\sigma \cong {\mathcal {T}}_{h(\tau )}$
there is an automorphism f that switches
![]() $\sigma $
with
$\sigma $
with
![]() $h(\tau )$
and all points outside of
$h(\tau )$
and all points outside of
![]() ${\mathcal {T}}_\sigma $
and
${\mathcal {T}}_\sigma $
and
![]() ${\mathcal {T}}_{h(\tau )}$
are fixed. Composing these automorphisms appropriately, we obtain that
${\mathcal {T}}_{h(\tau )}$
are fixed. Composing these automorphisms appropriately, we obtain that
![]() $h^{-1}(f(\sigma ))=\tau $
, so
$h^{-1}(f(\sigma ))=\tau $
, so
![]() $\tau $
is in the automorphism orbit of
$\tau $
is in the automorphism orbit of
![]() $\sigma $
. Thus,
$\sigma $
. Thus,
![]() $\varphi $
gives a
$\varphi $
gives a
![]() $\Sigma ^{\mathrm {in}}_{\gamma }$
definition of the automorphism orbit of
$\Sigma ^{\mathrm {in}}_{\gamma }$
definition of the automorphism orbit of
![]() $\sigma $
as required.
$\sigma $
as required.
Theorem 2.6 can be viewed as a strengthening of a result of Gao. He showed, using a different definition of Scott rank, that the ranks of
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() ${\mathcal {T}}_{\mathcal {A}}$
can be at most
${\mathcal {T}}_{\mathcal {A}}$
can be at most
![]() $\omega ^2$
apart [Reference Gao11].
$\omega ^2$
apart [Reference Gao11].
We now turn our attention to the parameterized Scott rank. Unlike the unparameterized case, parameterized Scott rank will not be preserved. To see this, we first need the following definitions. Given a tree T with root r and a tuple
![]() $\bar {c}=(c_1,\dots ,c_n)\in T$
, we say that
$\bar {c}=(c_1,\dots ,c_n)\in T$
, we say that
![]() $y\in T$
is somewhat comparable to
$y\in T$
is somewhat comparable to
![]() $\bar {c}$
if
$\bar {c}$
if
![]() $\exists z,i ~ z\neq r\land c_i\succeq z \land y\succeq z$
. A tuple is somewhat comparable to
$\exists z,i ~ z\neq r\land c_i\succeq z \land y\succeq z$
. A tuple is somewhat comparable to
![]() $\bar {c}$
if all of its points are. Similarly, we say that a point is entirely incomparable to
$\bar {c}$
if all of its points are. Similarly, we say that a point is entirely incomparable to
![]() $\bar {c}$
if it is not somewhat comparable to
$\bar {c}$
if it is not somewhat comparable to
![]() $\bar {c}$
and that a tuple is entirely incomparable to
$\bar {c}$
and that a tuple is entirely incomparable to
![]() $\bar {c}$
if all of its points are entirely incomparable to
$\bar {c}$
if all of its points are entirely incomparable to
![]() $\bar {c}$
. Note that if two elements are somewhat comparable, they must have a length 1 predecessor in common.
$\bar {c}$
. Note that if two elements are somewhat comparable, they must have a length 1 predecessor in common.
Lemma 2.7. For
![]() ${\mathcal {T}}_{\mathcal {A}}$
a tree of tuples, every
${\mathcal {T}}_{\mathcal {A}}$
a tree of tuples, every
![]() $\alpha \in \omega _1$
and tuples
$\alpha \in \omega _1$
and tuples
![]() $\bar a$
and
$\bar a$
and
![]() $\bar b$
that are entirely incomparable to
$\bar b$
that are entirely incomparable to
![]() $\bar p$
,
$\bar p$
,
Proof. We go by transfinite induction on
![]() $\alpha $
. The
$\alpha $
. The
![]() $\alpha =0$
case is immediate, as is the limit case. Assume the result for
$\alpha =0$
case is immediate, as is the limit case. Assume the result for
![]() $\alpha =\beta $
. If
$\alpha =\beta $
. If
![]() $\bar a\bar p\leq _{\beta +1}\bar b\bar p$
, then
$\bar a\bar p\leq _{\beta +1}\bar b\bar p$
, then
![]() $\bar a\leq _{\beta +1}\bar b$
follows immediately. Now assume that
$\bar a\leq _{\beta +1}\bar b$
follows immediately. Now assume that
![]() $\bar a\leq _{\beta +1}\bar b$
and consider an arbitrary tuple
$\bar a\leq _{\beta +1}\bar b$
and consider an arbitrary tuple
![]() $\bar c$
. We can split
$\bar c$
. We can split
![]() $\bar c$
into the points somewhat comparable to
$\bar c$
into the points somewhat comparable to
![]() $\bar p$
, named
$\bar p$
, named
![]() $\bar c_p$
, and the points entirely incomparable to
$\bar c_p$
, and the points entirely incomparable to
![]() $\bar p$
, named
$\bar p$
, named
![]() $\bar c_i$
(one of these may be the empty tuple). Because
$\bar c_i$
(one of these may be the empty tuple). Because
![]() $\bar a\leq _{\beta +1}\bar b$
, there is a tuple
$\bar a\leq _{\beta +1}\bar b$
, there is a tuple
![]() $\bar d_i$
such that
$\bar d_i$
such that
![]() $\bar a\bar d_i\geq _{\beta }\bar b\bar c_i$
. We show that we can find a
$\bar a\bar d_i\geq _{\beta }\bar b\bar c_i$
. We show that we can find a
![]() $\bar d^{\prime }_i$
that is entirely incomparable to
$\bar d^{\prime }_i$
that is entirely incomparable to
![]() $\bar p$
and has
$\bar p$
and has
![]() $\bar a\bar d^{\prime }_i\geq _{\beta }\bar b\bar c_i$
by modifying the given
$\bar a\bar d^{\prime }_i\geq _{\beta }\bar b\bar c_i$
by modifying the given
![]() $\bar d_i$
. Let
$\bar d_i$
. Let
![]() $p_1\dots p_n$
enumerate the length 1 points below any element in the tuple
$p_1\dots p_n$
enumerate the length 1 points below any element in the tuple
![]() $\bar p$
, and let
$\bar p$
, and let
![]() $a_1\dots a_n$
be similar for
$a_1\dots a_n$
be similar for
![]() $\bar a$
. Note that
$\bar a$
. Note that
![]() $p_1\dots p_n$
and
$p_1\dots p_n$
and
![]() $a_1\dots a_n$
do not intersect as
$a_1\dots a_n$
do not intersect as
![]() $\bar a$
is entirely incomparable to
$\bar a$
is entirely incomparable to
![]() $\bar p$
. We let
$\bar p$
. We let
![]() $d_1\dots d_n$
be similar for
$d_1\dots d_n$
be similar for
![]() $\bar d$
, but we remove the points that appear among
$\bar d$
, but we remove the points that appear among
![]() $a_1\dots a_n$
. For every
$a_1\dots a_n$
. For every
![]() $d_i$
let
$d_i$
let
![]() $d_i^{\prime }$
be an element with
$d_i^{\prime }$
be an element with
![]() ${\mathcal {T}}_{d_i}\cong {\mathcal {T}}_{d_i^{\prime }}$
that does not appear among the
${\mathcal {T}}_{d_i}\cong {\mathcal {T}}_{d_i^{\prime }}$
that does not appear among the
![]() $p_1\dots p_n$
and
$p_1\dots p_n$
and
![]() $a_1\dots a_n$
. This is possible because
$a_1\dots a_n$
. This is possible because
![]() ${\mathcal {T}}_{\mathcal {A}}$
is an infinitely replicated tree. Consider the automorphism
${\mathcal {T}}_{\mathcal {A}}$
is an infinitely replicated tree. Consider the automorphism
![]() $\Phi $
of
$\Phi $
of
![]() ${\mathcal {T}}_{\mathcal {A}}$
that exchanges
${\mathcal {T}}_{\mathcal {A}}$
that exchanges
![]() ${\mathcal {T}}_{d_i}$
and
${\mathcal {T}}_{d_i}$
and
![]() ${\mathcal {T}}_{d_i^{\prime }}$
but fixes all elements not among these subsets. We define
${\mathcal {T}}_{d_i^{\prime }}$
but fixes all elements not among these subsets. We define
![]() $\bar d^{\prime }_i=\Phi (\bar d)$
and claim that this tuple has the desired properties.
$\bar d^{\prime }_i=\Phi (\bar d)$
and claim that this tuple has the desired properties.
![]() $\Phi $
was constructed to fix
$\Phi $
was constructed to fix
![]() $\bar a$
; this means that
$\bar a$
; this means that
![]() $\bar d$
is automorphic to
$\bar d$
is automorphic to
![]() $\bar d'$
over
$\bar d'$
over
![]() $\bar a$
and therefore
$\bar a$
and therefore
![]() $\bar a\bar d^{\prime }_i\geq _{\beta }\bar a\bar d_i\geq _{\beta }\bar b\bar c_i$
. Furthermore, none of the
$\bar a\bar d^{\prime }_i\geq _{\beta }\bar a\bar d_i\geq _{\beta }\bar b\bar c_i$
. Furthermore, none of the
![]() $d^{\prime }_i$
are among the
$d^{\prime }_i$
are among the
![]() $p_i$
by construction so
$p_i$
by construction so
![]() $\bar d'$
and
$\bar d'$
and
![]() $\bar p$
are entirely incomparable. We can now note that
$\bar p$
are entirely incomparable. We can now note that
![]() $\bar a\bar d^{\prime }_i$
and
$\bar a\bar d^{\prime }_i$
and
![]() $\bar b\bar c_i$
are entirely incomparable with
$\bar b\bar c_i$
are entirely incomparable with
![]() $\bar p\bar c_p$
as somewhat comparability is an equivalence relation. In particular, the induction hypothesis gives that
$\bar p\bar c_p$
as somewhat comparability is an equivalence relation. In particular, the induction hypothesis gives that
Rearranging the tuples gives that
which shows that
![]() $\bar a\bar p\leq _{\beta +1}\bar b\bar p$
, as desired.
$\bar a\bar p\leq _{\beta +1}\bar b\bar p$
, as desired.
Lemma 2.8. For every tree of tuples
![]() ${\mathcal {T}}_{\mathcal {A}}$
,
${\mathcal {T}}_{\mathcal {A}}$
,
![]() $SR({\mathcal {T}}_{\mathcal {A}})=pSR({\mathcal {T}}_{\mathcal {A}})$
.
$SR({\mathcal {T}}_{\mathcal {A}})=pSR({\mathcal {T}}_{\mathcal {A}})$
.
Proof. Consider a tuple
![]() $\bar a$
that is
$\bar a$
that is
![]() $\alpha $
-free in
$\alpha $
-free in
![]() ${\mathcal {T}}_{\mathcal {A}}$
. Without loss of generality (by picking parameters automorphic to
${\mathcal {T}}_{\mathcal {A}}$
. Without loss of generality (by picking parameters automorphic to
![]() $\bar p$
) we have that
$\bar p$
) we have that
![]() $\bar a$
is entirely incomparable with
$\bar a$
is entirely incomparable with
![]() $\bar p$
. We demonstrate that
$\bar p$
. We demonstrate that
![]() $\bar a$
is also
$\bar a$
is also
![]() $\alpha $
-free in
$\alpha $
-free in
![]() $({\mathcal {T}}_{\mathcal {A}},\bar p)$
.
$({\mathcal {T}}_{\mathcal {A}},\bar p)$
.
Consider
![]() $\bar b\in {\mathcal {T}}_{\mathcal {A}}$
and
$\bar b\in {\mathcal {T}}_{\mathcal {A}}$
and
![]() $\beta <\alpha $
. We wish to show that there are
$\beta <\alpha $
. We wish to show that there are
![]() $\bar a',\bar b'$
such that
$\bar a',\bar b'$
such that
![]() $\bar a\bar b\bar p\leq _\beta \bar a'\bar b'\bar p$
and
$\bar a\bar b\bar p\leq _\beta \bar a'\bar b'\bar p$
and
![]() $\bar a\bar p\not \leq _\alpha \bar a'\bar p.$
$\bar a\bar p\not \leq _\alpha \bar a'\bar p.$
We can split
![]() $\bar b$
into the points somewhat comparable to
$\bar b$
into the points somewhat comparable to
![]() $\bar p$
, named
$\bar p$
, named
![]() $\bar b_p$
, and the points entirely incomparable to
$\bar b_p$
, and the points entirely incomparable to
![]() $\bar p$
, named
$\bar p$
, named
![]() $\bar b_i$
(one of these may be the empty tuple). Using the
$\bar b_i$
(one of these may be the empty tuple). Using the
![]() $\alpha $
-freeness of
$\alpha $
-freeness of
![]() $\bar a$
in
$\bar a$
in
![]() ${\mathcal {T}}_{\mathcal {A}}$
, we may find
${\mathcal {T}}_{\mathcal {A}}$
, we may find
![]() $\bar a'$
and
$\bar a'$
and
![]() $\bar b_i^{\prime }$
(entirely incomparable to p via an automorphism fixing
$\bar b_i^{\prime }$
(entirely incomparable to p via an automorphism fixing
![]() $\bar a$
) such that
$\bar a$
) such that
![]() $\bar a\bar b_i\leq _\beta \bar a'\bar b_i^{\prime }$
and
$\bar a\bar b_i\leq _\beta \bar a'\bar b_i^{\prime }$
and
![]() $\bar a\not \leq _\alpha \bar a'.$
$\bar a\not \leq _\alpha \bar a'.$
It follows from the previous lemma that
![]() $\bar a\bar b_i\bar p\bar b_p\leq _\beta \bar a'\bar b_i^{\prime }\bar p\bar b_p$
and
$\bar a\bar b_i\bar p\bar b_p\leq _\beta \bar a'\bar b_i^{\prime }\bar p\bar b_p$
and
![]() $\bar a\bar p\not \leq _\alpha \bar a'\bar p.$
Rearranging the tuples we get that
$\bar a\bar p\not \leq _\alpha \bar a'\bar p.$
Rearranging the tuples we get that
![]() $\bar a\bar b\bar p\leq _\beta \bar a'\bar b'\bar p$
and
$\bar a\bar b\bar p\leq _\beta \bar a'\bar b'\bar p$
and
![]() $\bar a\bar p\not \leq _\alpha \bar a'\bar p.$
Therefore,
$\bar a\bar p\not \leq _\alpha \bar a'\bar p.$
Therefore,
![]() $\bar a$
is also
$\bar a$
is also
![]() $\alpha $
-free in
$\alpha $
-free in
![]() $({\mathcal {T}}_{\mathcal {A}},\bar p)$
.
$({\mathcal {T}}_{\mathcal {A}},\bar p)$
.
In particular, if there are no
![]() $\alpha $
-free tuples in
$\alpha $
-free tuples in
![]() $({\mathcal {T}}_{\mathcal {A}},\bar p)$
then there are no
$({\mathcal {T}}_{\mathcal {A}},\bar p)$
then there are no
![]() $\alpha $
-free tuples in
$\alpha $
-free tuples in
![]() ${\mathcal {T}}_{\mathcal {A}}$
. Hence,
${\mathcal {T}}_{\mathcal {A}}$
. Hence,
![]() $SR({\mathcal {T}}_{\mathcal {A}})=pSR({\mathcal {T}}_{\mathcal {A}})$
.
$SR({\mathcal {T}}_{\mathcal {A}})=pSR({\mathcal {T}}_{\mathcal {A}})$
.
The previous two results can be used to understand the effect of the Friedman–Stanley embedding on Scott sentence complexity in all but the limit cases. We use the following new technique to deal with these cases.
Definition 2.9. For a structure
![]() $\mathcal {A}$
and a limit ordinal
$\mathcal {A}$
and a limit ordinal
![]() $\lambda $
, a
$\lambda $
, a
![]() $\lambda $
-sequence in
$\lambda $
-sequence in
![]() $\mathcal {A}$
is a set of tuples
$\mathcal {A}$
is a set of tuples
![]() $\bar y_i\in \mathcal {A}$
for
$\bar y_i\in \mathcal {A}$
for
![]() $i\in \omega $
such that
$i\in \omega $
such that
![]() $\bar y_i\equiv _{\alpha _i}\bar y_{i+1}$
for some fundamental sequence
$\bar y_i\equiv _{\alpha _i}\bar y_{i+1}$
for some fundamental sequence
![]() $(\alpha _i)_{i\in \omega }$
for
$(\alpha _i)_{i\in \omega }$
for
![]() $\lambda $
. We say that a
$\lambda $
. We say that a
![]() $\lambda $
-sequence is unstable if
$\lambda $
-sequence is unstable if
![]() $y_i\not \equiv _{\alpha _{i+1}}y_{i+1}$
.
$y_i\not \equiv _{\alpha _{i+1}}y_{i+1}$
.
Lemma 2.10. Consider a structure
![]() $\mathcal {A}$
with
$\mathcal {A}$
with
![]() $SR(\mathcal {A})=\lambda $
for
$SR(\mathcal {A})=\lambda $
for
![]() $\lambda $
a limit ordinal. The Scott sentence complexity of
$\lambda $
a limit ordinal. The Scott sentence complexity of
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
if and only if there are no unstable
$\Pi ^{\mathrm {in}}_{\lambda }$
if and only if there are no unstable
![]() $\lambda $
-sequences in
$\lambda $
-sequences in
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof. We start with the right to left implication and argue by contraposition. Assume
![]() $SR(\mathcal {A})=\lambda $
, yet
$SR(\mathcal {A})=\lambda $
, yet
![]() $\mathcal {A}$
does not have a
$\mathcal {A}$
does not have a
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
Scott sentence. Then there is a structure
$\Pi ^{\mathrm {in}}_{\lambda }$
Scott sentence. Then there is a structure
![]() $\mathcal {B}$
such that
$\mathcal {B}$
such that
![]() $\mathcal {A}\equiv _\lambda \mathcal {B}$
yet
$\mathcal {A}\equiv _\lambda \mathcal {B}$
yet
![]() $\mathcal {A}\not \cong \mathcal {B}$
. Because
$\mathcal {A}\not \cong \mathcal {B}$
. Because
![]() $\mathcal {A}$
has Scott rank
$\mathcal {A}$
has Scott rank
![]() $\lambda $
this is equivalent to saying that
$\lambda $
this is equivalent to saying that
![]() $\mathcal {A}\equiv _\lambda \mathcal {B}$
yet
$\mathcal {A}\equiv _\lambda \mathcal {B}$
yet
![]() $\mathcal {A}\not \leq _{\lambda +1} \mathcal {B}$
. In other words, there is a tuple
$\mathcal {A}\not \leq _{\lambda +1} \mathcal {B}$
. In other words, there is a tuple
![]() $\bar x\in \mathcal {B}$
such that for any
$\bar x\in \mathcal {B}$
such that for any
![]() $\bar z\in \mathcal {A}$
,
$\bar z\in \mathcal {A}$
,
![]() $\bar z\not \equiv _\lambda \bar x$
. However, as
$\bar z\not \equiv _\lambda \bar x$
. However, as
![]() $\mathcal {A}\equiv _\lambda \mathcal {B}$
, given a fundamental sequence
$\mathcal {A}\equiv _\lambda \mathcal {B}$
, given a fundamental sequence
![]() $(\alpha _i)_{i\in \omega }$
for
$(\alpha _i)_{i\in \omega }$
for
![]() $\lambda $
, for every i there is some
$\lambda $
, for every i there is some
![]() $\bar y_i\in \mathcal {A}$
such that
$\bar y_i\in \mathcal {A}$
such that
![]() $\bar y_i\equiv _{\alpha _i} \bar x$
. It follows that the
$\bar y_i\equiv _{\alpha _i} \bar x$
. It follows that the
![]() $\bar y_i$
are a
$\bar y_i$
are a
![]() $\lambda $
-sequence. Furthermore, given any i, there must be some
$\lambda $
-sequence. Furthermore, given any i, there must be some
![]() $k>i$
such that
$k>i$
such that
![]() $\bar y_i\not \equiv _{\alpha _{k}}\bar y_{k}$
. Otherwise,
$\bar y_i\not \equiv _{\alpha _{k}}\bar y_{k}$
. Otherwise,
![]() $\bar y_i\equiv _\lambda \bar x$
, a contradiction to the choice of
$\bar y_i\equiv _\lambda \bar x$
, a contradiction to the choice of
![]() $\bar x$
. The above k can be taken to equal
$\bar x$
. The above k can be taken to equal
![]() $i+1$
if we thin out the sequence by removing intermediate elements between i and k. In particular, the sequence
$i+1$
if we thin out the sequence by removing intermediate elements between i and k. In particular, the sequence
![]() $(\bar y_i)_{i\in \omega }$
can be taken to be unstable.
$(\bar y_i)_{i\in \omega }$
can be taken to be unstable.
We now prove the left to right implication, again by contraposition. Consider a structure
![]() $\mathcal {A}$
with an unstable
$\mathcal {A}$
with an unstable
![]() $\lambda $
-sequence
$\lambda $
-sequence
![]() $(\bar y_i)_{i\in \omega }$
. Consider the sequence of structures given by
$(\bar y_i)_{i\in \omega }$
. Consider the sequence of structures given by
![]() $(\mathcal {A},\bar y_i)_{i\in \omega }$
. By [Reference Montalbán21, Lemma XII.6], there is a structure
$(\mathcal {A},\bar y_i)_{i\in \omega }$
. By [Reference Montalbán21, Lemma XII.6], there is a structure
![]() $\mathcal {B}$
and tuple
$\mathcal {B}$
and tuple
![]() $\bar z\in \mathcal {B}$
such that for each i,
$\bar z\in \mathcal {B}$
such that for each i,
![]() $(\mathcal {B},\bar z)\equiv _{\alpha _i}(\mathcal {A},\bar y_{i})$
. Note that, in particular, this means that
$(\mathcal {B},\bar z)\equiv _{\alpha _i}(\mathcal {A},\bar y_{i})$
. Note that, in particular, this means that
![]() $\mathcal {B}\equiv _\lambda \mathcal {A}$
. Furthermore, for each i there is some
$\mathcal {B}\equiv _\lambda \mathcal {A}$
. Furthermore, for each i there is some
![]() $k>i$
such that
$k>i$
such that
![]() $\alpha _k\geq 2\alpha _i+3$
, as the difference between
$\alpha _k\geq 2\alpha _i+3$
, as the difference between
![]() $2\alpha _i+3$
and
$2\alpha _i+3$
and
![]() $\alpha _i$
is finite. For this k, we can observe that
$\alpha _i$
is finite. For this k, we can observe that
By [Reference Montalbán21, Lemma VI.14] this is a
![]() $\Sigma ^{\mathrm {in}}_{2\alpha _i+3}$
sentence that is computable in
$\Sigma ^{\mathrm {in}}_{2\alpha _i+3}$
sentence that is computable in
![]() $\mathcal {A}$
. As
$\mathcal {A}$
. As
![]() $(\mathcal {B},\bar z)\equiv _{\alpha _k}(\mathcal {A},\bar y_k)$
, by choice of k,
$(\mathcal {B},\bar z)\equiv _{\alpha _k}(\mathcal {A},\bar y_k)$
, by choice of k,
Now consider the automorphism orbit of
![]() $\bar z$
inside
$\bar z$
inside
![]() $\mathcal {B}$
. It cannot be defined by a
$\mathcal {B}$
. It cannot be defined by a
![]() $\Sigma ^{\mathrm {in}}_{\beta }$
formula for
$\Sigma ^{\mathrm {in}}_{\beta }$
formula for
![]() $\beta <\lambda $
, as if we take
$\beta <\lambda $
, as if we take
![]() $\alpha _i>\beta $
, by the above observation, there is a tuple that is not in the automorphism orbit of
$\alpha _i>\beta $
, by the above observation, there is a tuple that is not in the automorphism orbit of
![]() $\bar z$
that is
$\bar z$
that is
![]() $\alpha _i$
-equivalent to
$\alpha _i$
-equivalent to
![]() $\bar z$
. This means that
$\bar z$
. This means that
![]() $SR(\mathcal {B})>\lambda $
so
$SR(\mathcal {B})>\lambda $
so
![]() $\mathcal {B}\not \cong \mathcal {A}$
. As
$\mathcal {B}\not \cong \mathcal {A}$
. As
![]() $\mathcal {B}\equiv _\lambda \mathcal {A}$
, there is no
$\mathcal {B}\equiv _\lambda \mathcal {A}$
, there is no
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
Scott sentence for A.
$\Pi ^{\mathrm {in}}_{\lambda }$
Scott sentence for A.
The former lemma can be better understood as an internal compactness property that is present in structures with Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
. For the sake of completeness we include this equivalent formulation here.
$\Pi ^{\mathrm {in}}_{\lambda }$
. For the sake of completeness we include this equivalent formulation here.
Corollary 2.11. Consider a structure
![]() $\mathcal {A}$
with
$\mathcal {A}$
with
![]() $SR(\mathcal {A})=\lambda $
for
$SR(\mathcal {A})=\lambda $
for
![]() $\lambda $
a limit ordinal. Then the following are equivalent.
$\lambda $
a limit ordinal. Then the following are equivalent.
-
(1)
 $\mathcal {A}$
has Scott sentence complexity
$\mathcal {A}$
has Scott sentence complexity
 $\Pi ^{\mathrm {in}}_{\lambda }$
.
$\Pi ^{\mathrm {in}}_{\lambda }$
. -
(2) For every fundamental sequence
 $(\delta _n)_{n\in \omega }$
for
$(\delta _n)_{n\in \omega }$
for
 $\lambda $
and complete
$\lambda $
and complete
 $\delta _n$
-types
$\delta _n$
-types
 $p_n(\bar x)$
with m free variables for some m and
$p_n(\bar x)$
with m free variables for some m and
 $p_n\subset p_{n+1}$
, every type
$p_n\subset p_{n+1}$
, every type
 $p_n$
is realized in
$p_n$
is realized in
 $\mathcal {A}$
if and only if there is
$\mathcal {A}$
if and only if there is
 $\bar a\in A^m$
realizing every type
$\bar a\in A^m$
realizing every type
 $p_n$
.
$p_n$
.
Proof. Say
![]() $\mathcal {A}$
has Scott sentence complexity
$\mathcal {A}$
has Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
and fix
$\Pi ^{\mathrm {in}}_{\lambda }$
and fix
![]() $m\in \omega $
. If
$m\in \omega $
. If
![]() $\mathcal {A}$
realizes all the
$\mathcal {A}$
realizes all the
![]() $\delta _n$
-types
$\delta _n$
-types
![]() $p_n(\bar x)$
with m free variables and
$p_n(\bar x)$
with m free variables and
![]() $p_n\subset p_{n+1}$
, then any sequence of elements
$p_n\subset p_{n+1}$
, then any sequence of elements
![]() $(\bar y_n)_n\in \omega $
such that
$(\bar y_n)_n\in \omega $
such that
![]() $\bar y_n$
realizes the type
$\bar y_n$
realizes the type
![]() $p_n(\bar x)$
forms a
$p_n(\bar x)$
forms a
![]() $\lambda $
-sequence. If
$\lambda $
-sequence. If
![]() $\bar y_n\not \equiv _{\delta _{k}} \bar y_{k}$
for
$\bar y_n\not \equiv _{\delta _{k}} \bar y_{k}$
for
![]() $k>n$
on a cofinal subset, then we can obtain an unstable sequence by thinning out the sequence, a contradiction. Therefore, there is some K for which
$k>n$
on a cofinal subset, then we can obtain an unstable sequence by thinning out the sequence, a contradiction. Therefore, there is some K for which
![]() $\bar y_n\equiv _{\delta _{k}} \bar y_{k}$
for all
$\bar y_n\equiv _{\delta _{k}} \bar y_{k}$
for all
![]() $k>n\geq K$
. Then
$k>n\geq K$
. Then
![]() $\bar y_K$
realizes every type
$\bar y_K$
realizes every type
![]() $p_n$
.
$p_n$
.
On the other hand, if
![]() $\mathcal {A}$
does not have Scott sentence complexity
$\mathcal {A}$
does not have Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
it must have some unstable sequence,
$\Pi ^{\mathrm {in}}_{\lambda }$
it must have some unstable sequence,
![]() $(\bar z_n)_{n\in \omega }$
. If we take the
$(\bar z_n)_{n\in \omega }$
. If we take the
![]() $\delta _n$
-type of
$\delta _n$
-type of
![]() $\bar z_n$
to be
$\bar z_n$
to be
![]() $p_n$
, then clearly every type
$p_n$
, then clearly every type
![]() $p_n$
is realized in
$p_n$
is realized in
![]() $\mathcal {A}$
. However, if there is
$\mathcal {A}$
. However, if there is
![]() $\bar a$
that realizes all of the types
$\bar a$
that realizes all of the types
![]() $p_n$
, then we have that
$p_n$
, then we have that
![]() $\bar a\equiv _{\delta _n}\bar z_n$
yet
$\bar a\equiv _{\delta _n}\bar z_n$
yet
![]() $\bar a\not \equiv _{\delta _{n+1}}\bar z_{n+1}$
. Therefore the orbit of
$\bar a\not \equiv _{\delta _{n+1}}\bar z_{n+1}$
. Therefore the orbit of
![]() $\bar a$
is not
$\bar a$
is not
![]() $\Sigma ^{\mathrm {in}}_{\lambda }$
definable, a contradiction as
$\Sigma ^{\mathrm {in}}_{\lambda }$
definable, a contradiction as
![]() $SR(\mathcal {A})=\lambda $
.
$SR(\mathcal {A})=\lambda $
.
Note that this cannot be upgraded from complete types to general formulas. In other words, there may be a sequence of properly
![]() $\Pi ^{\mathrm {in}}_{\delta _n}$
formulas
$\Pi ^{\mathrm {in}}_{\delta _n}$
formulas
![]() $\varphi _n$
such that
$\varphi _n$
such that
![]() $\varphi _{n+1}\to \varphi _n$
and
$\varphi _{n+1}\to \varphi _n$
and ![]() yet
yet ![]() . To see this, we need not look past our example of a
. To see this, we need not look past our example of a
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
linear order for
$\Pi ^{\mathrm {in}}_{\lambda }$
linear order for
![]() $\lambda $
a limit given in Proposition 4.11. In particular the following formulas are a counterexample satisfied by this ordering:
$\lambda $
a limit given in Proposition 4.11. In particular the following formulas are a counterexample satisfied by this ordering:
We now note that unstable sequences transfer between a structure and its tree of tuples. This will allow us to resolve the final Scott sentence complexity ambiguity. In order to do this, we first need the following technical lemma.
Lemma 2.12. Let
![]() $S=(x_1,\dots ,x_n)$
and
$S=(x_1,\dots ,x_n)$
and
![]() $T=(y_1,\dots ,y_n)$
be (finite) isomorphic downward closed subsets of
$T=(y_1,\dots ,y_n)$
be (finite) isomorphic downward closed subsets of
![]() ${\mathcal {T}}_{\mathcal {A}}$
.
${\mathcal {T}}_{\mathcal {A}}$
.
![]() $S\leq _\alpha T$
if and only if for all i,
$S\leq _\alpha T$
if and only if for all i,
![]() $x_i\leq _\alpha y_i$
.
$x_i\leq _\alpha y_i$
.
Proof. If
![]() $S\leq _\alpha T$
,
$S\leq _\alpha T$
,
![]() $x_i\leq _\alpha y_i$
for any i follows immediately from the monotonicity of
$x_i\leq _\alpha y_i$
for any i follows immediately from the monotonicity of
![]() $\leq _\alpha $
.
$\leq _\alpha $
.
Say that for all i,
![]() $x_i\leq _\alpha y_i$
. Note that for all i,
$x_i\leq _\alpha y_i$
. Note that for all i,
![]() ${\mathcal {T}}_{ x_i}\leq _\alpha {\mathcal {T}}_{ y_i}$
. This holds because any
${\mathcal {T}}_{ x_i}\leq _\alpha {\mathcal {T}}_{ y_i}$
. This holds because any
![]() $\Pi ^{\mathrm {in}}_{\alpha }$
formula about
$\Pi ^{\mathrm {in}}_{\alpha }$
formula about
![]() ${\mathcal {T}}_{ x_i}$
can be transformed into a
${\mathcal {T}}_{ x_i}$
can be transformed into a
![]() $\Pi ^{\mathrm {in}}_{\alpha }$
formula about
$\Pi ^{\mathrm {in}}_{\alpha }$
formula about
![]() $x_i$
by restricting all quantifiers to being above
$x_i$
by restricting all quantifiers to being above
![]() $x_i$
. Let
$x_i$
. Let
 $$\begin{align*}{\mathcal{T}}^*_{x_i} := {\mathcal{T}}_{ x_i} - \left(\bigcup_{j : x_j \text{ is a child of } x_i} {\mathcal{T}}_{ x_j}\right) \quad\text{ and }\quad {\mathcal{T}}^*_{y_i} := {\mathcal{T}}_{ y_i} - \left(\bigcup_{j : y_j \text{ is a child of } y_i} {\mathcal{T}}_{ y_j}\right). \end{align*}$$
$$\begin{align*}{\mathcal{T}}^*_{x_i} := {\mathcal{T}}_{ x_i} - \left(\bigcup_{j : x_j \text{ is a child of } x_i} {\mathcal{T}}_{ x_j}\right) \quad\text{ and }\quad {\mathcal{T}}^*_{y_i} := {\mathcal{T}}_{ y_i} - \left(\bigcup_{j : y_j \text{ is a child of } y_i} {\mathcal{T}}_{ y_j}\right). \end{align*}$$
Note that
![]() ${\mathcal {T}}_{\mathcal {A}} = \sqcup _i {\mathcal {T}}^*_{x_i} = \sqcup _i {\mathcal {T}}^*_{y_i}$
as sets. By Lemma 2.5 we can observe that
${\mathcal {T}}_{\mathcal {A}} = \sqcup _i {\mathcal {T}}^*_{x_i} = \sqcup _i {\mathcal {T}}^*_{y_i}$
as sets. By Lemma 2.5 we can observe that
![]() ${\mathcal {T}}^*_{x_i}\cong {\mathcal {T}}_{ x_i}$
and
${\mathcal {T}}^*_{x_i}\cong {\mathcal {T}}_{ x_i}$
and
![]() ${\mathcal {T}}^*_{y_i}\cong {\mathcal {T}}_{ y_i}$
. In particular, this means that for all i,
${\mathcal {T}}^*_{y_i}\cong {\mathcal {T}}_{ y_i}$
. In particular, this means that for all i,
![]() ${\mathcal {T}}^*_{x_i}\leq _\alpha {\mathcal {T}}^*_{y_i}$
.
${\mathcal {T}}^*_{x_i}\leq _\alpha {\mathcal {T}}^*_{y_i}$
.
We have a sequence of strategies
![]() $\sigma _i$
where each
$\sigma _i$
where each
![]() $\sigma _i$
wins the back-and-forth game for the
$\sigma _i$
wins the back-and-forth game for the
![]() $\exists $
-player demonstrating that
$\exists $
-player demonstrating that
![]() ${\mathcal {T}}^*_{x_i}\leq _\alpha {\mathcal {T}}^*_{y_i}$
. We use these strategies to describe a winning strategy in the back-and-forth game for the
${\mathcal {T}}^*_{x_i}\leq _\alpha {\mathcal {T}}^*_{y_i}$
. We use these strategies to describe a winning strategy in the back-and-forth game for the
![]() $\exists $
-player demonstrating that
$\exists $
-player demonstrating that
![]() $S\leq _\alpha T$
. At any given even stage of the game the
$S\leq _\alpha T$
. At any given even stage of the game the
![]() $\forall $
-player will have played a tuple
$\forall $
-player will have played a tuple
![]() $(S,\bar d)$
. Write
$(S,\bar d)$
. Write
![]() $\bar d=(\bar d_1\dots \bar d_n)$
where
$\bar d=(\bar d_1\dots \bar d_n)$
where
![]() $\bar d_i$
is the (possibly empty) subset of
$\bar d_i$
is the (possibly empty) subset of
![]() $\bar d$
that is in
$\bar d$
that is in
![]() ${\mathcal {T}}^*_{y_i}$
. The
${\mathcal {T}}^*_{y_i}$
. The
![]() $\exists $
-player will play the move
$\exists $
-player will play the move
![]() $(T,\sigma _1(\bar d_1),\dots ,\sigma _n(\bar d_n))$
in response. The analogous strategy on the
$(T,\sigma _1(\bar d_1),\dots ,\sigma _n(\bar d_n))$
in response. The analogous strategy on the
![]() ${\mathcal {T}}^*_{x_i}$
is executed on the odd stages. In sum, the
${\mathcal {T}}^*_{x_i}$
is executed on the odd stages. In sum, the
![]() $\exists $
-player will play a winning strategy on each part of the partition
$\exists $
-player will play a winning strategy on each part of the partition
![]() ${\mathcal {T}}_{\mathcal {A}} = \sqcup _i {\mathcal {T}}^*_{x_i} = \sqcup _i {\mathcal {T}}^*_{y_i}$
completely agnostic of what is being played on the other parts of the partition.
${\mathcal {T}}_{\mathcal {A}} = \sqcup _i {\mathcal {T}}^*_{x_i} = \sqcup _i {\mathcal {T}}^*_{y_i}$
completely agnostic of what is being played on the other parts of the partition.
Consider tuples
![]() $(T,\bar a)$
and
$(T,\bar a)$
and
![]() $(S,\bar b)$
that are produced at the end of a play where the
$(S,\bar b)$
that are produced at the end of a play where the
![]() $\exists $
-player plays according to the above strategy. To confirm that the strategy is winning, we need to show that these tuples have the same atomic diagrams. Write
$\exists $
-player plays according to the above strategy. To confirm that the strategy is winning, we need to show that these tuples have the same atomic diagrams. Write
![]() $\bar a=(\bar a_1\dots \bar a_n)$
and
$\bar a=(\bar a_1\dots \bar a_n)$
and
![]() $\bar b=(\bar b_1\dots \bar b_n)$
where
$\bar b=(\bar b_1\dots \bar b_n)$
where
![]() $\bar a_i$
is the (possibly empty) subset of
$\bar a_i$
is the (possibly empty) subset of
![]() $\bar a$
that is in
$\bar a$
that is in
![]() ${\mathcal {T}}^*_{y_i}$
and
${\mathcal {T}}^*_{y_i}$
and
![]() $\bar b_i$
is the (possibly empty) subset of
$\bar b_i$
is the (possibly empty) subset of
![]() $\bar b$
that is in
$\bar b$
that is in
![]() ${\mathcal {T}}^*_{x_i}$
. Because we played a winning strategy on each of the parts of the partition
${\mathcal {T}}^*_{x_i}$
. Because we played a winning strategy on each of the parts of the partition
![]() ${\mathcal {T}}_{\mathcal {A}} = \sqcup _i {\mathcal {T}}^*_{x_i} = \sqcup _i {\mathcal {T}}^*_{y_i}$
, we know that for all i,
${\mathcal {T}}_{\mathcal {A}} = \sqcup _i {\mathcal {T}}^*_{x_i} = \sqcup _i {\mathcal {T}}^*_{y_i}$
, we know that for all i,
![]() $\bar a_i$
and
$\bar a_i$
and
![]() $\bar b_i$
have the same atomic diagram. We must only check that the binary relations between elements in different tuples
$\bar b_i$
have the same atomic diagram. We must only check that the binary relations between elements in different tuples
![]() $\bar a_i$
and
$\bar a_i$
and
![]() $\bar a_j$
are mirrored in the binary relations between
$\bar a_j$
are mirrored in the binary relations between
![]() $\bar b_i$
and
$\bar b_i$
and
![]() $\bar b_j$
and that the binary relations between
$\bar b_j$
and that the binary relations between
![]() $\bar a_i$
and T are mirrored in the binary relations between
$\bar a_i$
and T are mirrored in the binary relations between
![]() $\bar b_i$
and S. Note that no binary relations hold between elements of distinct
$\bar b_i$
and S. Note that no binary relations hold between elements of distinct
![]() $\bar a_i$
and
$\bar a_i$
and
![]() $\bar a_j$
as these elements are not comparable; the same is true for distinct
$\bar a_j$
as these elements are not comparable; the same is true for distinct
![]() $\bar b_i$
and
$\bar b_i$
and
![]() $\bar b_j$
. Given
$\bar b_j$
. Given
![]() $y_k\in T$
, it is less than all elements of
$y_k\in T$
, it is less than all elements of
![]() $\bar a_i$
if
$\bar a_i$
if
![]() $y_k\leq y_i$
and incomparable otherwise; the same is true for
$y_k\leq y_i$
and incomparable otherwise; the same is true for
![]() $x_k\in S$
and the elements of
$x_k\in S$
and the elements of
![]() $\bar b_i$
. This confirms that the binary relations between different parts of the tuples
$\bar b_i$
. This confirms that the binary relations between different parts of the tuples
![]() $(T,\bar a)$
and
$(T,\bar a)$
and
![]() $(S,\bar b)$
are the same in both cases. This means that the strategy is winning for the
$(S,\bar b)$
are the same in both cases. This means that the strategy is winning for the
![]() $\exists $
-player as claimed and
$\exists $
-player as claimed and
![]() $S\leq _\alpha T$
as desired.
$S\leq _\alpha T$
as desired.
Lemma 2.13. A structure
![]() $\mathcal {A}$
has an unstable
$\mathcal {A}$
has an unstable
![]() $\lambda $
-sequence if and only if its tree of tuples,
$\lambda $
-sequence if and only if its tree of tuples,
![]() ${\mathcal {T}}_{\mathcal {A}}$
does.
${\mathcal {T}}_{\mathcal {A}}$
does.
Proof. Consider an unstable
![]() $\lambda $
-sequence in
$\lambda $
-sequence in
![]() $\mathcal {A}$
given by
$\mathcal {A}$
given by
![]() $(\bar y_k)_{k\in \omega }$
. Say each tuple is coded by the element
$(\bar y_k)_{k\in \omega }$
. Say each tuple is coded by the element
![]() $m_k\in {\mathcal {T}}_{\mathcal {A}}$
, then Lemma 2.3 gives us at once that
$m_k\in {\mathcal {T}}_{\mathcal {A}}$
, then Lemma 2.3 gives us at once that
![]() $m_k$
is an unstable
$m_k$
is an unstable
![]() $\lambda $
-sequence.
$\lambda $
-sequence.
On the other hand, consider an unstable
![]() $\lambda $
-sequence in
$\lambda $
-sequence in
![]() ${\mathcal {T}}_{\mathcal {A}}$
given by the fundamental sequence
${\mathcal {T}}_{\mathcal {A}}$
given by the fundamental sequence
![]() $(\delta _k)_{k\in \omega }$
and associated tuples
$(\delta _k)_{k\in \omega }$
and associated tuples
![]() $(\bar z_k)_{i\in \omega }$
. Let
$(\bar z_k)_{i\in \omega }$
. Let
![]() $S_k$
denote the finite tree of elements less than or equal to some point in the tuple,
$S_k$
denote the finite tree of elements less than or equal to some point in the tuple,
![]() $\bar z_k$
. Note that the isomorphism type of
$\bar z_k$
. Note that the isomorphism type of
![]() $S_k$
is fixed so long as we have without loss of generality that
$S_k$
is fixed so long as we have without loss of generality that
![]() $\delta _k>1$
for all k. By the definition of unstable
$\delta _k>1$
for all k. By the definition of unstable
![]() $\lambda $
-sequences we have that
$\lambda $
-sequences we have that
By picking all of the elements in
![]() $S_k$
or
$S_k$
or
![]() $S_{k+1}$
as the first move of a back-and-forth game, we obtain that
$S_{k+1}$
as the first move of a back-and-forth game, we obtain that
It follows from Lemma 2.12 that by reducing to some reindexed fundamental subsequence of
![]() $(\delta _k)_{k\in \omega }$
, say
$(\delta _k)_{k\in \omega }$
, say
![]() $(\gamma _k)_{k\in \omega }$
, we have that for some sequence of points
$(\gamma _k)_{k\in \omega }$
, we have that for some sequence of points
![]() $x_k \in S_k$
$x_k \in S_k$
By Lemma 2.3, the
![]() $\bar y_k$
coded by the
$\bar y_k$
coded by the
![]() $x_k$
, satisfy
$x_k$
, satisfy
Therefore, there is an unstable
![]() $\lambda $
-sequence in
$\lambda $
-sequence in
![]() $\mathcal {A}$
. Together, we obtain the desired result.
$\mathcal {A}$
. Together, we obtain the desired result.
Corollary 2.14.
A has Scott sentence complexity
![]() $\Pi _\lambda ^{in}$
if and only if
$\Pi _\lambda ^{in}$
if and only if
![]() $T_A$
has Scott sentence complexity
$T_A$
has Scott sentence complexity
![]() $\Pi _\lambda ^{in}$
.
$\Pi _\lambda ^{in}$
.
Corollary 2.15. If
![]() $\mathcal {A}$
has Scott sentence complexity
$\mathcal {A}$
has Scott sentence complexity
![]() $\Gamma _\beta ^{\mathrm {in}}$
,
$\Gamma _\beta ^{\mathrm {in}}$
,
![]() ${\mathcal {T}}_{\mathcal {A}}$
has Scott sentence complexity
${\mathcal {T}}_{\mathcal {A}}$
has Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\alpha }$
where
$\Pi ^{\mathrm {in}}_{\alpha }$
where
![]() $\alpha =\beta $
if
$\alpha =\beta $
if
![]() $\Gamma =\Pi $
and
$\Gamma =\Pi $
and
![]() $\alpha =\beta +1$
otherwise.
$\alpha =\beta +1$
otherwise.
Proof. If
![]() $SR(\mathcal {A})=SR({\mathcal {T}}_{\mathcal {A}})$
is not a limit ordinal, then it follows from
$SR(\mathcal {A})=SR({\mathcal {T}}_{\mathcal {A}})$
is not a limit ordinal, then it follows from
![]() $SR({\mathcal {T}}_{\mathcal {A}})=pSR({\mathcal {T}}_{\mathcal {A}})$
that
$SR({\mathcal {T}}_{\mathcal {A}})=pSR({\mathcal {T}}_{\mathcal {A}})$
that
![]() ${\mathcal {T}}_{\mathcal {A}}$
has
${\mathcal {T}}_{\mathcal {A}}$
has
![]() $\Pi ^{\mathrm {in}}_{SR(\mathcal {A})+1}$
Scott sentence complexity.
$\Pi ^{\mathrm {in}}_{SR(\mathcal {A})+1}$
Scott sentence complexity.
If
![]() $SR(\mathcal {A})=SR({\mathcal {T}}_{\mathcal {A}})=\lambda $
is a limit ordinal, then by Corollary 2.14
$SR(\mathcal {A})=SR({\mathcal {T}}_{\mathcal {A}})=\lambda $
is a limit ordinal, then by Corollary 2.14
![]() $SSC(\mathcal {A})=\Pi ^{\mathrm {in}}_{\lambda }$
if and only if
$SSC(\mathcal {A})=\Pi ^{\mathrm {in}}_{\lambda }$
if and only if
![]() $SSC({\mathcal {T}}_{\mathcal {A}})=\Pi ^{\mathrm {in}}_{\lambda }$
.
$SSC({\mathcal {T}}_{\mathcal {A}})=\Pi ^{\mathrm {in}}_{\lambda }$
.
2.2 From tree of structures to linear orderings
We now turn our attention to the second step of the Friedman–Stanley embedding. Following Friedman and Stanley [Reference Friedman and Stanley8] we define the linear ordering
![]() $L(T)$
given a labeled tree as follows.
$L(T)$
given a labeled tree as follows.
Definition 2.16. Let T be a labeled tree with labeling function
![]() $l_T:T\to \omega $
and take the linear ordering
$l_T:T\to \omega $
and take the linear ordering
![]() $\mathbb {Q}^{<\omega }$
, given by the lexicographic order on finite strings of elements in
$\mathbb {Q}^{<\omega }$
, given by the lexicographic order on finite strings of elements in
![]() $\mathbb Q$
. We first define a map
$\mathbb Q$
. We first define a map
![]() $f:\mathbb {Q}^{<\omega }\to T$
by recursion as follows: Map the empty string to the root of T, then assuming we have defined
$f:\mathbb {Q}^{<\omega }\to T$
by recursion as follows: Map the empty string to the root of T, then assuming we have defined
![]() $f(\sigma )$
we define f on elements of the form
$f(\sigma )$
we define f on elements of the form
![]() $\sigma ^{\smallfrown } q$
for
$\sigma ^{\smallfrown } q$
for
![]() $q\in \mathbb {Q}$
to be a map from
$q\in \mathbb {Q}$
to be a map from
![]() $\mathbb {Q}$
to
$\mathbb {Q}$
to
![]() $\{\tau : \exists i\ \tau =\sigma ^{\smallfrown } i\}$
such that
$\{\tau : \exists i\ \tau =\sigma ^{\smallfrown } i\}$
such that
![]() $f^{-1}{\tau }$
is dense in
$f^{-1}{\tau }$
is dense in
![]() $\{\sigma ^{\smallfrown } q: q\in \mathbb {Q}\}$
. Then, for every
$\{\sigma ^{\smallfrown } q: q\in \mathbb {Q}\}$
. Then, for every
![]() $\sigma \in T$
, if
$\sigma \in T$
, if
![]() $l(\sigma )=n$
, then for every
$l(\sigma )=n$
, then for every
![]() $x\in f^{-1}(\sigma )$
, replace x by the finite linear ordering of size
$x\in f^{-1}(\sigma )$
, replace x by the finite linear ordering of size
![]() $n+2$
. If T is the tree of structures
$n+2$
. If T is the tree of structures
![]() ${\mathcal {T}}_{\mathcal {A}}$
of
${\mathcal {T}}_{\mathcal {A}}$
of
![]() $\mathcal {A}$
, then we refer to
$\mathcal {A}$
, then we refer to
![]() $L(T)$
as
$L(T)$
as
![]() $L_{\mathcal {A}}$
.
$L_{\mathcal {A}}$
.
Lemma 2.17. For every
![]() $\alpha $
and ordered
$\alpha $
and ordered
![]() $\bar a,\bar b\in L_{\mathcal {A}}$
such that if
$\bar a,\bar b\in L_{\mathcal {A}}$
such that if
![]() $a_i$
, or
$a_i$
, or
![]() $b_i$
are from a labeled block, then every element in this block is in
$b_i$
are from a labeled block, then every element in this block is in
![]() $\bar a$
, respectively
$\bar a$
, respectively
![]() $\bar b$
,
$\bar b$
,
![]() $\bar a\leq _{3+\alpha }\bar b$
if and only if
$\bar a\leq _{3+\alpha }\bar b$
if and only if
![]() $f(\bar a)\leq _{1+\alpha } f(\bar b)$
.
$f(\bar a)\leq _{1+\alpha } f(\bar b)$
.
Proof. The proof is by transfinite induction with the only interesting case being the base case. For this note that the label and predecessor relation of
![]() ${\mathcal {T}}_{\mathcal {A}}$
in
${\mathcal {T}}_{\mathcal {A}}$
in
![]() $L_{\mathcal {A}}$
are both
$L_{\mathcal {A}}$
are both
![]() $\Sigma ^{\mathrm {in}}_{3}$
and
$\Sigma ^{\mathrm {in}}_{3}$
and
![]() $\Pi ^{\mathrm {in}}_{3}$
definable in
$\Pi ^{\mathrm {in}}_{3}$
definable in
![]() $L_{{\mathcal {T}}_{\mathcal {A}}}$
. Let
$L_{{\mathcal {T}}_{\mathcal {A}}}$
. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Sigma ^{\mathrm {in}}_{1}$
formula true of
$\Sigma ^{\mathrm {in}}_{1}$
formula true of
![]() $\bar a$
, then this formula can be translated into a
$\bar a$
, then this formula can be translated into a
![]() $\Sigma ^{\mathrm {in}}_{3}$
formula true of
$\Sigma ^{\mathrm {in}}_{3}$
formula true of
![]() $f(\bar a)$
and thus
$f(\bar a)$
and thus
![]() $\bar a\leq _3 \bar b$
implies
$\bar a\leq _3 \bar b$
implies
![]() $f(\bar a)\leq _1 f(\bar b)$
.
$f(\bar a)\leq _1 f(\bar b)$
.
On the other hand, assume that
![]() $f(\bar a)\leq _1 f(\bar b)$
and without loss of generality that
$f(\bar a)\leq _1 f(\bar b)$
and without loss of generality that
![]() $\bar a$
and
$\bar a$
and
![]() $\bar b$
contain elements from exactly two different blocks. Let us consider the back-and-forth game where the
$\bar b$
contain elements from exactly two different blocks. Let us consider the back-and-forth game where the
![]() $\forall $
-player plays elements
$\forall $
-player plays elements
![]() $\bar b^1$
on their first turn. For every
$\bar b^1$
on their first turn. For every
![]() $b^1_i$
the
$b^1_i$
the
![]() $\exists $
-player looks for elements
$\exists $
-player looks for elements
![]() $a^1_i$
such that
$a^1_i$
such that
![]() $l(f(a^1_i))=l(f(b^1_i))$
,
$l(f(a^1_i))=l(f(b^1_i))$
,
![]() $a^1_i$
is in the same position in its block as
$a^1_i$
is in the same position in its block as
![]() $b^1_i$
and
$b^1_i$
and
![]() $\bar a\bar a^1$
and
$\bar a\bar a^1$
and
![]() $\bar b\bar b^1$
are isomorphic in the tree-ordering. Note that they will find a suitable
$\bar b\bar b^1$
are isomorphic in the tree-ordering. Note that they will find a suitable
![]() $\bar a^1$
because
$\bar a^1$
because
![]() $f(\bar a)\leq _1 f(\bar b)$
. Now on their last turn the
$f(\bar a)\leq _1 f(\bar b)$
. Now on their last turn the
![]() $\forall $
-player plays a tuple
$\forall $
-player plays a tuple
![]() $\bar a^2$
and the
$\bar a^2$
and the
![]() $\exists $
-player has to respond playing
$\exists $
-player has to respond playing
![]() $\bar b^2$
such that
$\bar b^2$
such that
![]() $\bar a\bar a^1\bar a^2\leq _1 \bar b\bar b^1\bar b^2$
. All they need to do is ensure that the intervals in
$\bar a\bar a^1\bar a^2\leq _1 \bar b\bar b^1\bar b^2$
. All they need to do is ensure that the intervals in
![]() $\bar a\bar a^1\bar a^2$
are at least as large as the intervals in
$\bar a\bar a^1\bar a^2$
are at least as large as the intervals in
![]() $\bar b\bar b^1\bar b^2$
. Between any two elements in different blocks in
$\bar b\bar b^1\bar b^2$
. Between any two elements in different blocks in
![]() $L_{\mathcal {A}}$
, there are blocks coding paths in
$L_{\mathcal {A}}$
, there are blocks coding paths in
![]() ${\mathcal {T}}_{\mathcal {A}}$
. Thus, between any two elements in different blocks there are blocks of arbitrary large size and thus the
${\mathcal {T}}_{\mathcal {A}}$
. Thus, between any two elements in different blocks there are blocks of arbitrary large size and thus the
![]() $\exists $
-player can find elements satisfying this requirement.
$\exists $
-player can find elements satisfying this requirement.
Lemma 2.18. For any structure
![]() $\mathcal {A}$
,
$\mathcal {A}$
,
![]() $2+SR({\mathcal {T}}_{\mathcal {A}})=SR(L_{\mathcal {A}})$
. In particular,
$2+SR({\mathcal {T}}_{\mathcal {A}})=SR(L_{\mathcal {A}})$
. In particular,
![]() ${\mathcal {T}}_{\mathcal {A}}$
has a
${\mathcal {T}}_{\mathcal {A}}$
has a
![]() $\Pi ^{\mathrm {in}}_{1+\alpha }$
Scott sentence if and only if
$\Pi ^{\mathrm {in}}_{1+\alpha }$
Scott sentence if and only if
![]() $L_{\mathcal {A}}$
has a
$L_{\mathcal {A}}$
has a
![]() $\Pi ^{\mathrm {in}}_{3+\alpha }$
Scott sentence.
$\Pi ^{\mathrm {in}}_{3+\alpha }$
Scott sentence.
Proof. For successor ordinals it is sufficient to note that Lemma 2.17 implies that a tuple
![]() $\bar a$
in
$\bar a$
in
![]() $L_{\mathcal {A}}$
is
$L_{\mathcal {A}}$
is
![]() $(3+\alpha )$
-free if and only if
$(3+\alpha )$
-free if and only if
![]() $f(\bar a)$
is
$f(\bar a)$
is
![]() $(1+\alpha )$
-free in
$(1+\alpha )$
-free in
![]() ${\mathcal {T}}_{\mathcal {A}}$
. Likewise, a tuple
${\mathcal {T}}_{\mathcal {A}}$
. Likewise, a tuple
![]() $\bar a$
is
$\bar a$
is
![]() $(1+\alpha )$
-free in
$(1+\alpha )$
-free in
![]() ${\mathcal {T}}_{\mathcal {A}}$
if and only if
${\mathcal {T}}_{\mathcal {A}}$
if and only if
![]() $f^{-1}(\bar a)$
is
$f^{-1}(\bar a)$
is
![]() $(3+\alpha )$
-free in
$(3+\alpha )$
-free in
![]() $L_{\mathcal {A}}$
.
$L_{\mathcal {A}}$
.
For
![]() $\alpha $
a limit, note that by Lemma 2.17 an
$\alpha $
a limit, note that by Lemma 2.17 an
![]() $\alpha $
-sequence for
$\alpha $
-sequence for
![]() $L_{\mathcal {A}}$
is unstable if and only if the pull-back along f is unstable in
$L_{\mathcal {A}}$
is unstable if and only if the pull-back along f is unstable in
![]() ${\mathcal {T}}_{\mathcal {A}}$
.
${\mathcal {T}}_{\mathcal {A}}$
.
Combining everything developed in this section we obtain the following.
Theorem 2.19. For
![]() $\alpha>\omega $
, the Friedman–Stanley embedding preserves parameterized Scott rank, but it does not preserve parameterless Scott rank. In particular, for any given structure
$\alpha>\omega $
, the Friedman–Stanley embedding preserves parameterized Scott rank, but it does not preserve parameterless Scott rank. In particular, for any given structure
![]() $\mathcal {A}$
and any ordinal
$\mathcal {A}$
and any ordinal
![]() $\alpha $
:
$\alpha $
:
-
(1) If
 $SSC(\mathcal {A})=\Pi ^{\mathrm {in}}_{1+\alpha }$
, then
$SSC(\mathcal {A})=\Pi ^{\mathrm {in}}_{1+\alpha }$
, then
 $SSC(L_{\mathcal {A}})=\Pi ^{\mathrm {in}}_{3+\alpha .}$
$SSC(L_{\mathcal {A}})=\Pi ^{\mathrm {in}}_{3+\alpha .}$
-
(2) If
 $SSC(\mathcal {A})=\Sigma ^{\mathrm {in}}_{1+\alpha }$
or
$SSC(\mathcal {A})=\Sigma ^{\mathrm {in}}_{1+\alpha }$
or
 $SSC(\mathcal {A})=d\text{-}\Sigma ^{\mathrm {in}}_{1+\alpha }$
, then
$SSC(\mathcal {A})=d\text{-}\Sigma ^{\mathrm {in}}_{1+\alpha }$
, then
 $SSC(L_{\mathcal {A}})=\Pi ^{\mathrm {in}}_{3+\alpha +1.}$
$SSC(L_{\mathcal {A}})=\Pi ^{\mathrm {in}}_{3+\alpha +1.}$
Another useful characterization of structures with Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
is that they are precisely those structures whose
$\Pi ^{\mathrm {in}}_{\lambda }$
is that they are precisely those structures whose
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
infinitary theory is
$\Pi ^{\mathrm {in}}_{\lambda }$
infinitary theory is
![]() $\aleph _0$
-categorical. Our results thus show the following.
$\aleph _0$
-categorical. Our results thus show the following.
Corollary 2.20. For any limit ordinal
![]() $\lambda $
and any structure
$\lambda $
and any structure
![]() $\mathcal {A}$
, the
$\mathcal {A}$
, the
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
infinitary theory of
$\Pi ^{\mathrm {in}}_{\lambda }$
infinitary theory of
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\aleph _0$
-categorical if and only if the
$\aleph _0$
-categorical if and only if the
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
theory of
$\Pi ^{\mathrm {in}}_{\lambda }$
theory of
![]() $L_{\mathcal {A}}$
is
$L_{\mathcal {A}}$
is
![]() $\aleph _0$
-categorical.
$\aleph _0$
-categorical.
The above corollary is related to a result by Calvert, Goncharov, and Knight who showed that there is a linear ordering of Scott rank
![]() $\omega _{1}^{\mathrm {CK}}$
by proving a “rank-preservation property” for computable embeddings [Reference Calvert, Goncharov and Knight7]. Their arguments show that the Friedman–Stanley embedding preserves
$\omega _{1}^{\mathrm {CK}}$
by proving a “rank-preservation property” for computable embeddings [Reference Calvert, Goncharov and Knight7]. Their arguments show that the Friedman–Stanley embedding preserves
![]() $\aleph _0$
-categoricity of the computable infinitary theory of structures. As a structure's computable infinitary theory is
$\aleph _0$
-categoricity of the computable infinitary theory of structures. As a structure's computable infinitary theory is
![]() $\aleph _0$
-categorical if and only if it has Scott rank
$\aleph _0$
-categorical if and only if it has Scott rank
![]() $\omega _{1}^{\mathrm {CK}}$
this shows that the Friedman–Stanley embedding preserves Scott rank at that level (see [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1]).
$\omega _{1}^{\mathrm {CK}}$
this shows that the Friedman–Stanley embedding preserves Scott rank at that level (see [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1]).
2.3 Remarks on effectivity
Some Borel reductions maintain Scott rank externally in the sense that they take sufficiently complex Borel isomorphism classes and push them forward to classes of equal complexity in the image space. In this case, Scott sentence complexity is preserved for sufficiently high complexities.
Proposition 2.21. If
![]() $\Phi :Mod(\sigma )\to Mod(\tau )$
is a Borel reduction such that
$\Phi :Mod(\sigma )\to Mod(\tau )$
is a Borel reduction such that
![]() $[\Phi (X)]_{\cong }$
is Borel and that eventually satisfies push-forward, i.e., there is
$[\Phi (X)]_{\cong }$
is Borel and that eventually satisfies push-forward, i.e., there is
![]() $\delta $
such that for
$\delta $
such that for
![]() $\gamma \geq \delta $
and
$\gamma \geq \delta $
and
![]() $\psi \in \Pi ^{\mathrm {in}}_{\gamma }$
there is
$\psi \in \Pi ^{\mathrm {in}}_{\gamma }$
there is
![]() $\psi ^*\in \Pi ^{\mathrm {in}}_{\gamma }$
such that
$\psi ^*\in \Pi ^{\mathrm {in}}_{\gamma }$
such that
then there is an ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $\text {SR}(\mathcal {A})\geq \alpha $
implies that
$\text {SR}(\mathcal {A})\geq \alpha $
implies that
Proof. Say
![]() $\Phi $
is
$\Phi $
is ![]() -measurable and the image of
-measurable and the image of
![]() $\Phi $
is
$\Phi $
is ![]() . Let
. Let
![]() $\chi \in \Pi ^{\mathrm {in}}_{\beta }$
describe the image of
$\chi \in \Pi ^{\mathrm {in}}_{\beta }$
describe the image of
![]() $\Phi $
in
$\Phi $
in
![]() $Mod(\tau )$
. Let
$Mod(\tau )$
. Let
![]() $\mathcal {A}$
have a
$\mathcal {A}$
have a
![]() $\Gamma ^{\mathrm {in}}_\gamma $
Scott sentence for
$\Gamma ^{\mathrm {in}}_\gamma $
Scott sentence for
![]() $\gamma>\delta $
, say
$\gamma>\delta $
, say
![]() $\varphi $
. Then
$\varphi $
. Then
![]() $\varphi ^*\land \chi $
is a
$\varphi ^*\land \chi $
is a
![]() $\Gamma ^{\mathrm {in}}_\gamma $
Scott sentence for
$\Gamma ^{\mathrm {in}}_\gamma $
Scott sentence for
![]() $\Phi (\mathcal {A})$
. On the other hand say
$\Phi (\mathcal {A})$
. On the other hand say
![]() $\Phi (\mathcal {A})$
has a
$\Phi (\mathcal {A})$
has a
![]() $\Gamma ^{\mathrm {in}}_\gamma $
Scott sentence for any
$\Gamma ^{\mathrm {in}}_\gamma $
Scott sentence for any
![]() $\gamma $
, then by the pullback theorem
$\gamma $
, then by the pullback theorem
![]() $\mathcal {A}$
has a
$\mathcal {A}$
has a
![]() $\Gamma ^{\mathrm {in}}_{\lambda +\gamma }$
Scott sentence. So for any
$\Gamma ^{\mathrm {in}}_{\lambda +\gamma }$
Scott sentence. So for any
![]() $\mathcal {A}$
with
$\mathcal {A}$
with
![]() $SR(\mathcal {A})>\max (\lambda \cdot \omega , \delta ,\beta )$
, Scott sentence complexity is preserved.
$SR(\mathcal {A})>\max (\lambda \cdot \omega , \delta ,\beta )$
, Scott sentence complexity is preserved.
Note that this proof has a straightforward effectivization. In particular, if
![]() $\Phi $
is hyperarithmetic and
$\Phi $
is hyperarithmetic and
![]() $\psi $
computable implies that
$\psi $
computable implies that
![]() $\psi ^*$
is computable, then the complexity of the simplest computable formula that describes the isomorphism type of
$\psi ^*$
is computable, then the complexity of the simplest computable formula that describes the isomorphism type of
![]() $\mathcal {A}$
is also preserved.
$\mathcal {A}$
is also preserved.
However, as we have seen in Theorem 2.19, the Friedman–Stanley embedding does not have the property that Scott sentence complexity is eventually preserved. We thus get the following corollary.
Corollary 2.22. The image of the Friedman–Stanley embedding is not a Borel subset of the class of linear orderings.
It should be noted that we can observe that the class of trees of structures is not Borel among the class of labeled trees directly. In particular, consider
![]() ${\mathcal {T}}_{\mathcal {A}}$
and
${\mathcal {T}}_{\mathcal {A}}$
and
![]() ${\mathcal {T}}_{\mathcal {B}}$
for structures with
${\mathcal {T}}_{\mathcal {B}}$
for structures with
![]() $\mathcal {A}\equiv _{\alpha +1} \mathcal {B}$
yet
$\mathcal {A}\equiv _{\alpha +1} \mathcal {B}$
yet
![]() $\mathcal {A}\not \cong \mathcal {B}$
. We can now define
$\mathcal {A}\not \cong \mathcal {B}$
. We can now define
![]() $T_{\mathcal {A},\mathcal {B}}:= {\mathcal {T}}_{\mathcal {A}}\sqcup _r{\mathcal {T}}_{\mathcal {B}}$
, the tree formed by identifying the roots of
$T_{\mathcal {A},\mathcal {B}}:= {\mathcal {T}}_{\mathcal {A}}\sqcup _r{\mathcal {T}}_{\mathcal {B}}$
, the tree formed by identifying the roots of
![]() ${\mathcal {T}}_{\mathcal {A}}$
and
${\mathcal {T}}_{\mathcal {A}}$
and
![]() ${\mathcal {T}}_{\mathcal {B}}$
and adding no other relations between them. Given our established criteria for
${\mathcal {T}}_{\mathcal {B}}$
and adding no other relations between them. Given our established criteria for
![]() $\equiv _\alpha $
, it is not difficult to show that
$\equiv _\alpha $
, it is not difficult to show that
![]() $T_{\mathcal {A},\mathcal {B}}\equiv _{\alpha }{\mathcal {T}}_{\mathcal {A}}\equiv _{\alpha }{\mathcal {T}}_{\mathcal {B}}$
. However,
$T_{\mathcal {A},\mathcal {B}}\equiv _{\alpha }{\mathcal {T}}_{\mathcal {A}}\equiv _{\alpha }{\mathcal {T}}_{\mathcal {B}}$
. However,
![]() $T_{\mathcal {A},\mathcal {B}}$
is not a tree of structures, as it lacks the property that comeager many paths represent the same structure. By taking
$T_{\mathcal {A},\mathcal {B}}$
is not a tree of structures, as it lacks the property that comeager many paths represent the same structure. By taking
![]() $\alpha $
arbitrarily large we can observe that there can be no
$\alpha $
arbitrarily large we can observe that there can be no
![]() $L_{\omega _1\omega }$
formula defining the class of tree of structures within the class of labeled trees.
$L_{\omega _1\omega }$
formula defining the class of tree of structures within the class of labeled trees.
This justifies why the proof of preservation of Scott rank proceeded as it did above. In particular, Scott rank was treated “internally” by looking at the definitions of automorphism orbits inside of the structure. Montalbán’s theorem on the robustness of the Scott rank [Reference Montalbán19] and the work of Alvir, Greenberg, Harrison-Trainor, and Turetsky [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1] allowed us to take this approach, as it provides a correspondence between the internal characterization of Scott sentence complexity and the external one. However, no such correspondence exists for computable formulas. Therefore, the proof technique used does not make it clear if there is a preservation of computable Scott rank.
The closest result to an effective version of Montalbán’s theorem is that of Alvir, Knight, and McCoy [Reference Alvir, Knight and McCoy2]. They prove the following.
Theorem 2.23. Let
![]() $\mathcal {A}$
be a computable structure and consider the following three properties:
$\mathcal {A}$
be a computable structure and consider the following three properties:
-
(1) There is a computable function f taking each tuple
 $\bar a$
to a computable
$\bar a$
to a computable
 $\Sigma ^{\mathrm {in}}_{\alpha }$
formula that defines its automorphism orbit.
$\Sigma ^{\mathrm {in}}_{\alpha }$
formula that defines its automorphism orbit. -
(2)
 $\mathcal {A}$
has a computable
$\mathcal {A}$
has a computable
 $\Pi ^{\mathrm {in}}_{\alpha +1}$
Scott sentence.
$\Pi ^{\mathrm {in}}_{\alpha +1}$
Scott sentence. -
(3) Every tuple in
 $\mathcal {A}$
has a computable
$\mathcal {A}$
has a computable
 $\Sigma ^{\mathrm {in}}_{\alpha }$
-definable automorphism orbit.
$\Sigma ^{\mathrm {in}}_{\alpha }$
-definable automorphism orbit.
Item 1 implies Item 2 implies Item 3.
Effectivizing our results in the previous section, it is not difficult to see that the Friedman–Stanley embedding preserves Item 1 and Item 3. However, preservation of Item 2 may need a different technique, or not be true at all. Alvir, Knight, and McCoy [Reference Alvir, Knight and McCoy2] ask to give a necessary and sufficient condition for a structure
![]() $\mathcal {A}$
to have a computable
$\mathcal {A}$
to have a computable
![]() $\Pi ^{\mathrm {in}}_{\alpha +1}$
Scott sentence. We offer the following variation closer connected to our studies.
$\Pi ^{\mathrm {in}}_{\alpha +1}$
Scott sentence. We offer the following variation closer connected to our studies.
Question 2.24. Does
![]() $\mathcal {A}$
have a computable
$\mathcal {A}$
have a computable
![]() $\Pi ^{\mathrm {in}}_{\alpha +1}$
Scott sentence if and only if
$\Pi ^{\mathrm {in}}_{\alpha +1}$
Scott sentence if and only if
![]() ${\mathcal {T}}_{\mathcal {A}}$
has a computable
${\mathcal {T}}_{\mathcal {A}}$
has a computable
![]() $\Pi ^{\mathrm {in}}_{\alpha +1}$
Scott sentence?
$\Pi ^{\mathrm {in}}_{\alpha +1}$
Scott sentence?
If this question has a positive answer, we suspect that the technique involved in proving this could be used to answer the question of Alvir, Knight, and McCoy.
3
 $\alpha $
-universality and linear orderings
$\alpha $
-universality and linear orderings
The main purpose of this section is to show that there is no linear ordering of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{3}$
and that there is no embedding from any class of structures into linear orderings that is simpler than the Friedman–Stanley embedding in the sense that it increases the Scott sentence complexity less.
$\Sigma ^{\mathrm {in}}_{3}$
and that there is no embedding from any class of structures into linear orderings that is simpler than the Friedman–Stanley embedding in the sense that it increases the Scott sentence complexity less.
In order to do this we introduce and study the following notion for the class of linear orderings.
Definition 3.1. Let
![]() $K_0\subseteq K_1$
be isomorphism invariant classes of structures. The class
$K_0\subseteq K_1$
be isomorphism invariant classes of structures. The class
![]() $K_0$
is
$K_0$
is
![]() $\alpha $
-universal for
$\alpha $
-universal for
![]() $K_1$
if for every
$K_1$
if for every
![]() $\mathcal {A}\in K_1$
there is
$\mathcal {A}\in K_1$
there is
![]() $\mathcal {B}\in K_0$
such that
$\mathcal {B}\in K_0$
such that
![]() $\mathcal {A}\leq _\alpha \mathcal {B}$
.
$\mathcal {A}\leq _\alpha \mathcal {B}$
.
Lemma 3.2. If
![]() $K_0$
is
$K_0$
is
![]() $\alpha $
-universal for
$\alpha $
-universal for
![]() $K_1$
, then
$K_1$
, then
![]() $K_0$
contains all structures in
$K_0$
contains all structures in
![]() $K_1$
with
$K_1$
with
![]() $\Pi ^{\mathrm {in}}_{\alpha }$
Scott sentences.
$\Pi ^{\mathrm {in}}_{\alpha }$
Scott sentences.
Proof. Consider
![]() $\mathcal {A}\in K_1$
with a
$\mathcal {A}\in K_1$
with a
![]() $\Pi ^{\mathrm {in}}_{\alpha }$
Scott sentence. By
$\Pi ^{\mathrm {in}}_{\alpha }$
Scott sentence. By
![]() $\alpha $
-universality, there is
$\alpha $
-universality, there is
![]() $\mathcal {B}\in K_0$
with
$\mathcal {B}\in K_0$
with
![]() $\mathcal {A}\leq _\alpha \mathcal {B}$
. But then
$\mathcal {A}\leq _\alpha \mathcal {B}$
. But then
![]() $\mathcal {A}\cong \mathcal {B}$
and thus
$\mathcal {A}\cong \mathcal {B}$
and thus
![]() $\mathcal {A}\in K_0$
, as
$\mathcal {A}\in K_0$
, as
![]() $K_0$
is isomorphism invariant.
$K_0$
is isomorphism invariant.
Corollary 3.3. If
![]() $K_0$
is
$K_0$
is
![]() $\alpha $
-universal for
$\alpha $
-universal for
![]() $K_1$
, then
$K_1$
, then
![]() $K_0$
contains all structures in
$K_0$
contains all structures in
![]() $K_1$
of parameterless Scott rank less than
$K_1$
of parameterless Scott rank less than
![]() $\alpha $
.
$\alpha $
.
Lemma 3.4. The class
![]() $K=\mathbb N\cup \{\mathbb {Q}\}$
is
$K=\mathbb N\cup \{\mathbb {Q}\}$
is
![]() $2$
-universal for
$2$
-universal for
![]() $\mathrm {LO}$
. In particular,
$\mathrm {LO}$
. In particular,
![]() $\{\mathbb {Q}\}$
is
$\{\mathbb {Q}\}$
is
![]() $2$
-universal for infinite linear orderings.
$2$
-universal for infinite linear orderings.
Proof. Let
![]() $\mathcal {A}\in \mathrm {LO}$
. If
$\mathcal {A}\in \mathrm {LO}$
. If
![]() $\mathcal {A}$
is finite then
$\mathcal {A}$
is finite then
![]() $\mathcal {A}\in K$
. If
$\mathcal {A}\in K$
. If
![]() $\mathcal {A}$
is infinite then we claim that
$\mathcal {A}$
is infinite then we claim that
![]() $\mathcal {A}\leq _2\mathbb {Q}$
. As any interval I in
$\mathcal {A}\leq _2\mathbb {Q}$
. As any interval I in
![]() $\mathbb {Q}$
is infinite we have that
$\mathbb {Q}$
is infinite we have that
![]() $I\leq _1\mathcal {A}_0$
for any interval
$I\leq _1\mathcal {A}_0$
for any interval
![]() $\mathcal {A}_0$
of
$\mathcal {A}_0$
of
![]() $\mathcal {A}$
. Thus,
$\mathcal {A}$
. Thus,
![]() $\mathcal {A}\leq _2\mathbb {Q}$
and, hence, K is
$\mathcal {A}\leq _2\mathbb {Q}$
and, hence, K is
![]() $2$
-universal.
$2$
-universal.
3.1
 $\Sigma ^{\mathrm {in}}_{3}$
is not the Scott sentence complexity of a linear ordering
$\Sigma ^{\mathrm {in}}_{3}$
is not the Scott sentence complexity of a linear ordering
Alvir, Greenberg, Harrison-Trainor, and Turetsky [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1] showed that no countable structure has Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{2}$
and that no infinite countable structure has a
$\Sigma ^{\mathrm {in}}_{2}$
and that no infinite countable structure has a
![]() $d\text{-}\Sigma ^{\mathrm {in}}_{1}$
Scott sentence. Thus, the first
$d\text{-}\Sigma ^{\mathrm {in}}_{1}$
Scott sentence. Thus, the first
![]() $\Sigma $
Scott sentence complexity attainable by a countable structure is
$\Sigma $
Scott sentence complexity attainable by a countable structure is
![]() $\Sigma ^{\mathrm {in}}_{3}$
.
$\Sigma ^{\mathrm {in}}_{3}$
.
Remmel [Reference Remmel23] showed that the computably categorical linear orderings are precisely those with finite adjacency relation. It is well-known that the computably categorical linear orderings and the relatively computably categorical linear orderings coincide [Reference Frolov10]. Both of these results relativize and thus one gets that the linear orderings with
![]() $\Sigma ^{\mathrm {in}}_{3}$
Scott sentences are precisely those with finite adjacency relation. For the convenience of the reader we give a simple proof using
$\Sigma ^{\mathrm {in}}_{3}$
Scott sentences are precisely those with finite adjacency relation. For the convenience of the reader we give a simple proof using
![]() $2$
-universality.
$2$
-universality.
Theorem 3.5. A linear ordering has a
![]() $\Sigma ^{\mathrm {in}}_{3}$
Scott sentence if and only if its adjacency relation is finite.
$\Sigma ^{\mathrm {in}}_{3}$
Scott sentence if and only if its adjacency relation is finite.
Proof. Say
![]() $\mathcal {A}\in \mathrm {LO}$
has a
$\mathcal {A}\in \mathrm {LO}$
has a
![]() $\Sigma ^{\mathrm {in}}_{3}$
Scott sentence, then by Table 1 there is a parameter
$\Sigma ^{\mathrm {in}}_{3}$
Scott sentence, then by Table 1 there is a parameter
![]() $\bar p\in A^{<\omega }$
such that
$\bar p\in A^{<\omega }$
such that
![]() $(\mathcal {A},\bar p)$
has a
$(\mathcal {A},\bar p)$
has a
![]() $\Pi ^{\mathrm {in}}_{2}$
Scott sentence. By the
$\Pi ^{\mathrm {in}}_{2}$
Scott sentence. By the
![]() $2$
-universality of
$2$
-universality of
![]() $\mathbb N\cup \{\mathbb {Q}\}$
every interval induced by
$\mathbb N\cup \{\mathbb {Q}\}$
every interval induced by
![]() $\bar p$
is isomorphic to either
$\bar p$
is isomorphic to either
![]() $\mathbb {Q}$
or n. Hence,
$\mathbb {Q}$
or n. Hence,
![]() $\mathcal {A}$
has at most finitely many adjacencies.
$\mathcal {A}$
has at most finitely many adjacencies.
On the other hand, say that
![]() $Adj^{\mathcal {A}}$
is finite and let
$Adj^{\mathcal {A}}$
is finite and let
![]() $\bar p$
be the ordered tuple of elements in the field of
$\bar p$
be the ordered tuple of elements in the field of
![]() $Adj^{\mathcal {A}}$
. Then every interval induced by
$Adj^{\mathcal {A}}$
. Then every interval induced by
![]() $\bar p$
is either empty or isomorphic to
$\bar p$
is either empty or isomorphic to
![]() $\mathbb {Q}$
. As
$\mathbb {Q}$
. As
![]() $\mathbb {Q}$
has a
$\mathbb {Q}$
has a
![]() $\Pi ^{\mathrm {in}}_{2}$
Scott sentence,
$\Pi ^{\mathrm {in}}_{2}$
Scott sentence,
![]() $(\mathcal {A},\bar p)$
has parameterless Scott rank
$(\mathcal {A},\bar p)$
has parameterless Scott rank
![]() $1$
,
$1$
,
![]() $\mathcal {A}$
has parameterized Scott rank
$\mathcal {A}$
has parameterized Scott rank
![]() $2$
, and, thus a
$2$
, and, thus a
![]() $\Sigma ^{\mathrm {in}}_{3}$
Scott sentence.
$\Sigma ^{\mathrm {in}}_{3}$
Scott sentence.
Theorem 3.6. No linear ordering has Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{3}$
.
$\Sigma ^{\mathrm {in}}_{3}$
.
Proof. The only candidates for linear orderings with Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{3}$
are by Theorem 3.5 those with finite adjacency relation. Now, these linear orderings are either finite, isomorphic to
$\Sigma ^{\mathrm {in}}_{3}$
are by Theorem 3.5 those with finite adjacency relation. Now, these linear orderings are either finite, isomorphic to
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $1+\mathbb {Q}$
,
$1+\mathbb {Q}$
,
![]() $\mathbb {Q}+1$
,
$\mathbb {Q}+1$
,
![]() $1+\mathbb {Q}+1$
, or isomorphic to a linear ordering obtained by replacing finitely many points in one of these four orderings by finite intervals. All but the last case are well-known to have
$1+\mathbb {Q}+1$
, or isomorphic to a linear ordering obtained by replacing finitely many points in one of these four orderings by finite intervals. All but the last case are well-known to have
![]() $\Pi ^{\mathrm {in}}_{3}$
Scott sentences and thus can not have Scott sentence complexity
$\Pi ^{\mathrm {in}}_{3}$
Scott sentences and thus can not have Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{3}$
. Consider an ordering whose order type falls in the last case, and that, without loss of generality, its order type is
$\Sigma ^{\mathrm {in}}_{3}$
. Consider an ordering whose order type falls in the last case, and that, without loss of generality, its order type is
![]() $n_1+\mathbb {Q}+n_2+\mathbb {Q}+n_3+\mathbb {Q}+\dots +n_k$
. Let
$n_1+\mathbb {Q}+n_2+\mathbb {Q}+n_3+\mathbb {Q}+\dots +n_k$
. Let
![]() $N=\sum _{i\leq k} n_i$
and assume that x is the jth element in the ordered tuple containing all the successor chains. Then its orbit is defined by
$N=\sum _{i\leq k} n_i$
and assume that x is the jth element in the ordered tuple containing all the successor chains. Then its orbit is defined by
 $$\begin{align*}\exists x_1\dots x_N\forall y\left(y\geq x_1\land x_{j}=x \land \bigwedge_{i<j,i\not\in \{ n_1,n_1+n_2,\dots,N\}} S(x_i,x_{i+1})\right),\end{align*}$$
$$\begin{align*}\exists x_1\dots x_N\forall y\left(y\geq x_1\land x_{j}=x \land \bigwedge_{i<j,i\not\in \{ n_1,n_1+n_2,\dots,N\}} S(x_i,x_{i+1})\right),\end{align*}$$
where S is the
![]() $\Pi ^0_1$
definable successor relation. The formula is
$\Pi ^0_1$
definable successor relation. The formula is
![]() $\Sigma ^{\mathrm {in}}_{2}$
and defines the orbit of the jth element in the successor chains as required. Now, let x be an element in the jth
$\Sigma ^{\mathrm {in}}_{2}$
and defines the orbit of the jth element in the successor chains as required. Now, let x be an element in the jth
![]() $\mathbb {Q}$
copy where
$\mathbb {Q}$
copy where
![]() $i=\sum _{l\leq j} n_l$
. Then its automorphism orbit is defined by
$i=\sum _{l\leq j} n_l$
. Then its automorphism orbit is defined by
 $$\begin{align*}\exists x_1\dots x_{N}\left(\bigwedge_{j<N, j\not\in \{ n_1,n_1+n_2,\dots,N\}} S(x_j,x_{j+1}) \land x_{i}<x<x_{i+1}\right)\end{align*}$$
$$\begin{align*}\exists x_1\dots x_{N}\left(\bigwedge_{j<N, j\not\in \{ n_1,n_1+n_2,\dots,N\}} S(x_j,x_{j+1}) \land x_{i}<x<x_{i+1}\right)\end{align*}$$
and this definition is again
![]() $\Sigma ^{\mathrm {in}}_{2}$
. It is easy to see that the defining formula of the automorphism orbit of any ordered tuple is just the conjunction of the defining formulas of the automorphism orbits of its elements. Thus,
$\Sigma ^{\mathrm {in}}_{2}$
. It is easy to see that the defining formula of the automorphism orbit of any ordered tuple is just the conjunction of the defining formulas of the automorphism orbits of its elements. Thus,
![]() $n_1+\mathbb {Q}+n_2+\mathbb {Q}+\dots +n_k$
has a
$n_1+\mathbb {Q}+n_2+\mathbb {Q}+\dots +n_k$
has a
![]() $\Pi ^{\mathrm {in}}_{3}$
Scott sentence.
$\Pi ^{\mathrm {in}}_{3}$
Scott sentence.
3.2 3-universality and optimality of the Friedman–Stanley embedding
Theorem 3.7. The following class is
![]() $3$
-universal for the class of linear orderings
$3$
-universal for the class of linear orderings
![]() $K=\{\omega +k, k+\omega ^*, k+\mathbb {Z}+k':k,k'\in \mathbb N\}\cup \{\omega +\omega ^*\}\cup \{(\sum _{i\in k} n_i + m_i\cdot \mathbb {Q} )+n_{k+1}:n_i,m_i\in \mathbb N, n_i>m_{i-1},m_{i+1}\}\cup \{k:k\in \mathbb N\}$
. There is no
$K=\{\omega +k, k+\omega ^*, k+\mathbb {Z}+k':k,k'\in \mathbb N\}\cup \{\omega +\omega ^*\}\cup \{(\sum _{i\in k} n_i + m_i\cdot \mathbb {Q} )+n_{k+1}:n_i,m_i\in \mathbb N, n_i>m_{i-1},m_{i+1}\}\cup \{k:k\in \mathbb N\}$
. There is no
![]() $3$
-universal class
$3$
-universal class
![]() $J\subset K$
.
$J\subset K$
.
Proof. Given a linear ordering
![]() $\mathcal {L}$
we can write
$\mathcal {L}$
we can write
![]() $\mathcal {L}=W+\mathcal {K}+R$
with W well ordered or empty, R reverse well ordered or empty, and
$\mathcal {L}=W+\mathcal {K}+R$
with W well ordered or empty, R reverse well ordered or empty, and
![]() $\mathcal {K}$
empty or without a greatest or least element.
$\mathcal {K}$
empty or without a greatest or least element.
The element in K that
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $\leq _3$
-below will depend on the sizes of W and R, and the order type of
$\leq _3$
-below will depend on the sizes of W and R, and the order type of
![]() $\mathcal {K}$
. Let us consider the different cases.
$\mathcal {K}$
. Let us consider the different cases.
Case 1. W is infinite and R is finite. In this case,
![]() $W=\omega +\alpha $
for some ordinal
$W=\omega +\alpha $
for some ordinal
![]() $\alpha $
, so
$\alpha $
, so
![]() $\mathcal {L}=\omega +\mathcal {K}'+k$
for some
$\mathcal {L}=\omega +\mathcal {K}'+k$
for some
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $\mathcal {K}'$
is either empty or without greatest element. We claim that
$\mathcal {K}'$
is either empty or without greatest element. We claim that
![]() $\mathcal {L}\leq _3\omega +k$
. It is sufficient to show that
$\mathcal {L}\leq _3\omega +k$
. It is sufficient to show that
![]() $\omega +\mathcal {K}'\leq _3\omega $
. The
$\omega +\mathcal {K}'\leq _3\omega $
. The
![]() $\exists $
-player always wins the corresponding back-and-forth game by playing the following strategy. In the first round they play isomorphically on the initial
$\exists $
-player always wins the corresponding back-and-forth game by playing the following strategy. In the first round they play isomorphically on the initial
![]() $\omega $
. Because of that they only need to win the back-and-forth game for
$\omega $
. Because of that they only need to win the back-and-forth game for
![]() $\omega \leq _2 \omega +\mathcal {K}'$
. Say the
$\omega \leq _2 \omega +\mathcal {K}'$
. Say the
![]() $\forall $
-player picks elements such that
$\forall $
-player picks elements such that
![]() $\omega +\mathcal {K}'$
is partitioned into n intervals
$\omega +\mathcal {K}'$
is partitioned into n intervals
![]() $\mathcal {A}_i$
, each of cardinality
$\mathcal {A}_i$
, each of cardinality
![]() $m_i$
for
$m_i$
for
![]() $i<n$
where
$i<n$
where
![]() $m_i$
might be infinite. The
$m_i$
might be infinite. The
![]() $\exists $
-player must pick a partition of
$\exists $
-player must pick a partition of
![]() $\omega $
such that for all intervals
$\omega $
such that for all intervals
![]() $\mathcal {B}_i$
, each of cardinality
$\mathcal {B}_i$
, each of cardinality
![]() $k_i$
,
$k_i$
,
![]() $\mathcal {A}_i\leq _1 \mathcal {B}_i$
. This inequality holds if and only if
$\mathcal {A}_i\leq _1 \mathcal {B}_i$
. This inequality holds if and only if
![]() $m_i\geq k_i$
. Given this inequality, the intervals formed by picking the first n elements of
$m_i\geq k_i$
. Given this inequality, the intervals formed by picking the first n elements of
![]() $\omega $
clearly form the desired partition.
$\omega $
clearly form the desired partition.
Case 2. W is finite and R is infinite. This case is analogous to the first case.
Case 3. Both W and R are infinite. In this case, we can write
![]() $\mathcal {L}=\omega +\mathcal {K}'+\omega ^*$
. We claim that
$\mathcal {L}=\omega +\mathcal {K}'+\omega ^*$
. We claim that
![]() $\mathcal {L}\leq _3 \omega +\omega ^*$
. The winning strategy for the
$\mathcal {L}\leq _3 \omega +\omega ^*$
. The winning strategy for the
![]() $\exists $
-player is similar to the one for Case 1. In the first play they play isomorphically on the initial
$\exists $
-player is similar to the one for Case 1. In the first play they play isomorphically on the initial
![]() $\omega $
and final
$\omega $
and final
![]() $\omega ^*$
to reduce the game to showing that
$\omega ^*$
to reduce the game to showing that
![]() $\omega +\omega ^*\leq _2 \omega +\mathcal {K}'+\omega ^*$
. They can then win this game by picking partitions with smaller intervals, exactly as above.
$\omega +\omega ^*\leq _2 \omega +\mathcal {K}'+\omega ^*$
. They can then win this game by picking partitions with smaller intervals, exactly as above.
Case 4. Both W and R are finite. There are two subcases with different behavior here. In both we assume that
![]() $\mathcal {K}$
has no greatest and least element, as if it was empty, then
$\mathcal {K}$
has no greatest and least element, as if it was empty, then
![]() $\mathcal {L}$
would be finite and thus isomorphic to a structure in K.
$\mathcal {L}$
would be finite and thus isomorphic to a structure in K.
Subcase 1. There are arbitrarily large successor chains in
![]() $\mathcal {K}$
. Here we claim that
$\mathcal {K}$
. Here we claim that
![]() $\mathcal {K}\leq _3\mathbb {Z}$
, which gives that
$\mathcal {K}\leq _3\mathbb {Z}$
, which gives that
![]() $\mathcal {L}\leq _3 k+\mathbb {Z}+k'$
for
$\mathcal {L}\leq _3 k+\mathbb {Z}+k'$
for
![]() $k,k'\in \mathbb {N}$
. The
$k,k'\in \mathbb {N}$
. The
![]() $\exists $
-player always wins the corresponding game by playing the following strategy. Assume the
$\exists $
-player always wins the corresponding game by playing the following strategy. Assume the
![]() $\forall $
-player plays an ordered tuple with the distance between least and greatest element n. Then the
$\forall $
-player plays an ordered tuple with the distance between least and greatest element n. Then the
![]() $\exists $
-player plays a successor chain of size n in
$\exists $
-player plays a successor chain of size n in
![]() $\mathcal {K}$
such that
$\mathcal {K}$
such that
![]() $\mathcal {K}=\mathcal {K}_1+n+\mathcal {K}_2$
where
$\mathcal {K}=\mathcal {K}_1+n+\mathcal {K}_2$
where
![]() $\mathcal {K}_1$
has no first element and
$\mathcal {K}_1$
has no first element and
![]() $\mathcal {K}_2$
has no last element. It is then sufficient to show that
$\mathcal {K}_2$
has no last element. It is then sufficient to show that
![]() $\omega ^*\leq _2 \mathcal {K}_1$
and
$\omega ^*\leq _2 \mathcal {K}_1$
and
![]() $\omega \leq _2 \mathcal {K}_2$
. In these games, similar to the cases above, the
$\omega \leq _2 \mathcal {K}_2$
. In these games, similar to the cases above, the
![]() $\exists $
-player just needs to ensure that they play partitions of smaller size then the
$\exists $
-player just needs to ensure that they play partitions of smaller size then the
![]() $\forall $
-player and this is possible by the same strategy.
$\forall $
-player and this is possible by the same strategy.
Subcase 2. There is an
![]() $n\in \mathbb N$
such that no element in
$n\in \mathbb N$
such that no element in
![]() $\mathcal {K}$
has n successors. In this case, we consider the block relation
$\mathcal {K}$
has n successors. In this case, we consider the block relation
![]() $\sim $
given by
$\sim $
given by
![]() $a\sim b$
if and only if
$a\sim b$
if and only if
![]() $[a,b]$
and
$[a,b]$
and
![]() $[b,a]$
are finite. By assumption every block is a linear ordering of size n or less. As no block can be infinite, no two blocks can be successors in the quotient
$[b,a]$
are finite. By assumption every block is a linear ordering of size n or less. As no block can be infinite, no two blocks can be successors in the quotient
![]() $\mathcal {K}/{\sim }$
. Furthermore, as there is no least or greatest element, there are no least or greatest blocks in
$\mathcal {K}/{\sim }$
. Furthermore, as there is no least or greatest element, there are no least or greatest blocks in
![]() $\mathcal {K}/{\sim }$
. Therefore,
$\mathcal {K}/{\sim }$
. Therefore,
![]() $\mathcal {K}/{\sim }=\mathbb {Q}$
. In total, this means that
$\mathcal {K}/{\sim }=\mathbb {Q}$
. In total, this means that
![]() $\mathcal {K}=\sum _{q\in \mathbb {Q}} i_n(q)$
where
$\mathcal {K}=\sum _{q\in \mathbb {Q}} i_n(q)$
where
![]() $i_n:\mathbb {Q}\to \{1,\dots , n\}$
. If there are only finitely many blocks of size n, we may write
$i_n:\mathbb {Q}\to \{1,\dots , n\}$
. If there are only finitely many blocks of size n, we may write
![]() $\mathcal {K}$
as a sum
$\mathcal {K}$
as a sum
![]() $\mathcal {K}_1+n+\cdots +n+\mathcal {K}_l$
where no block of size n occurs in any of the
$\mathcal {K}_1+n+\cdots +n+\mathcal {K}_l$
where no block of size n occurs in any of the
![]() $\mathcal {K}_i$
. Repeating this process as necessary, we can write
$\mathcal {K}_i$
. Repeating this process as necessary, we can write
![]() $\mathcal {K}$
as
$\mathcal {K}$
as
![]() $\mathcal {K}_1+n_1+\mathcal {K}_2+n_2+\dots \mathcal {K}_l$
where each
$\mathcal {K}_1+n_1+\mathcal {K}_2+n_2+\dots \mathcal {K}_l$
where each
![]() $\mathcal {K}_i$
is given by
$\mathcal {K}_i$
is given by
![]() $\mathcal {K}_i=\sum _{q\in (b_i,t_i)} i_n(q)$
where
$\mathcal {K}_i=\sum _{q\in (b_i,t_i)} i_n(q)$
where
![]() $t_i$
is the smallest element of
$t_i$
is the smallest element of
![]() $n_i$
and
$n_i$
and
![]() $b_i$
is the largest element of
$b_i$
is the largest element of
![]() $n_{i-1}$
or
$n_{i-1}$
or
![]() $-\infty $
if
$-\infty $
if
![]() $i=1$
such that
$i=1$
such that
![]() $\{ q\in (b_i,t_i): i_n(q)=m_i\}$
is infinite for
$\{ q\in (b_i,t_i): i_n(q)=m_i\}$
is infinite for
![]() $m_i=\max {\text {range}(i_n\operatorname {\mathrm {\upharpoonright }} (b_i,t_i))}$
. Furthermore, we have that
$m_i=\max {\text {range}(i_n\operatorname {\mathrm {\upharpoonright }} (b_i,t_i))}$
. Furthermore, we have that
![]() $m_i<n_i$
and if
$m_i<n_i$
and if
![]() $i>1$
,
$i>1$
,
![]() $m_i<n_{i-1}$
.
$m_i<n_{i-1}$
.
We now show that
![]() $\mathcal {L}=k{\kern-1pt}+{\kern-1pt}\mathcal {K}_1{\kern-1pt}+{\kern-1pt}n_1+\dots \mathcal {K}_l{\kern-1pt}+{\kern-1pt}k'\leq _3 k{\kern-1pt}+{\kern-1pt}m_1\cdot \mathbb {Q}+n_1\dots m_l\cdot \mathbb {Q}{\kern-1pt}+{\kern-1pt}k'$
. It is enough to show that
$\mathcal {L}=k{\kern-1pt}+{\kern-1pt}\mathcal {K}_1{\kern-1pt}+{\kern-1pt}n_1+\dots \mathcal {K}_l{\kern-1pt}+{\kern-1pt}k'\leq _3 k{\kern-1pt}+{\kern-1pt}m_1\cdot \mathbb {Q}+n_1\dots m_l\cdot \mathbb {Q}{\kern-1pt}+{\kern-1pt}k'$
. It is enough to show that
![]() $\mathcal {K}_i=\sum _{q\in (b_i,t_i)}i_n(q) \leq _3 m_i\cdot \mathbb {Q}$
. The
$\mathcal {K}_i=\sum _{q\in (b_i,t_i)}i_n(q) \leq _3 m_i\cdot \mathbb {Q}$
. The
![]() $\exists $
-player always wins this game by playing the following strategy. Every element the
$\exists $
-player always wins this game by playing the following strategy. Every element the
![]() $\forall $
-player plays in the first play is in a block of size
$\forall $
-player plays in the first play is in a block of size
![]() $m_i$
. The
$m_i$
. The
![]() $\exists $
-player can respond by playing elements in the same position in blocks of size
$\exists $
-player can respond by playing elements in the same position in blocks of size
![]() $m_i$
. The resulting intervals in
$m_i$
. The resulting intervals in
![]() $\mathcal {K}_i$
are of the form
$\mathcal {K}_i$
are of the form
![]() $l_1+\sum _{q\in (b_i^j,t_i^j)}i_n(q)+l_2$
where
$l_1+\sum _{q\in (b_i^j,t_i^j)}i_n(q)+l_2$
where
![]() $b_i^j> b_i$
and
$b_i^j> b_i$
and
![]() $t_i^j<t_i$
. The corresponding intervals in
$t_i^j<t_i$
. The corresponding intervals in
![]() $m_i\cdot \mathbb {Q}$
are of the form
$m_i\cdot \mathbb {Q}$
are of the form
![]() $l_1+m_i\cdot \mathbb {Q}+l_2$
. Winning the game thus comes down to finding a winning strategy for the game
$l_1+m_i\cdot \mathbb {Q}+l_2$
. Winning the game thus comes down to finding a winning strategy for the game
![]() $m_i\cdot \mathbb {Q}\leq _2 \sum _{q\in (b_i^j,t_i^j)}i_n(q)$
. Given a partition in
$m_i\cdot \mathbb {Q}\leq _2 \sum _{q\in (b_i^j,t_i^j)}i_n(q)$
. Given a partition in
![]() $\sum _{q\in (b_i^j,t_i^j)}i_n(q)$
, the
$\sum _{q\in (b_i^j,t_i^j)}i_n(q)$
, the
![]() $\exists $
-player needs to find a partition in
$\exists $
-player needs to find a partition in
![]() $m_i\cdot \mathbb {Q}$
such that all intervals are smaller than the intervals in the partition picked by the
$m_i\cdot \mathbb {Q}$
such that all intervals are smaller than the intervals in the partition picked by the
![]() $\forall $
-player. They can do that using the fact that the finite blocks are densely ordered and always of maximum size.
$\forall $
-player. They can do that using the fact that the finite blocks are densely ordered and always of maximum size.
This shows that K is
![]() $3$
-universal. Standard arguments show that each element of K has a
$3$
-universal. Standard arguments show that each element of K has a
![]() $\Pi ^{\mathrm {in}}_{3}$
Scott sentence. Therefore, by Lemma 3.2, there is no
$\Pi ^{\mathrm {in}}_{3}$
Scott sentence. Therefore, by Lemma 3.2, there is no
![]() $J\subset K$
such that J is
$J\subset K$
such that J is
![]() $3$
-universal.
$3$
-universal.
Note that McCoy [Reference McCoy18] obtained a similar characterization for the linear orderings that are
![]() $\Delta ^0_2$
categorical. Theorem 3.7 can be used to show a boldface version of this result.
$\Delta ^0_2$
categorical. Theorem 3.7 can be used to show a boldface version of this result.
Corollary 3.8. If
![]() $\mathcal {L}$
is a linear ordering with a
$\mathcal {L}$
is a linear ordering with a
![]() $\Pi ^{\mathrm {in}}_{3}$
Scott sentence, then
$\Pi ^{\mathrm {in}}_{3}$
Scott sentence, then
![]() $\mathcal {L}$
is in K.
$\mathcal {L}$
is in K.
Since by Table 1 and Lemma 1.4 every linear ordering with a
![]() $\Sigma ^{\mathrm {in}}_{4}$
Scott sentence is sum of linear orderings with
$\Sigma ^{\mathrm {in}}_{4}$
Scott sentence is sum of linear orderings with
![]() $\Pi ^{\mathrm {in}}_{3}$
Scott sentences we obtain the following.
$\Pi ^{\mathrm {in}}_{3}$
Scott sentences we obtain the following.
Corollary 3.9. If
![]() $\mathcal {L}$
is a linear ordering with a
$\mathcal {L}$
is a linear ordering with a
![]() $\Sigma ^{\mathrm {in}}_{4}$
Scott sentence, then
$\Sigma ^{\mathrm {in}}_{4}$
Scott sentence, then
![]() $\mathcal {L}$
is a finite sum of linear orderings in K.
$\mathcal {L}$
is a finite sum of linear orderings in K.
That the Friedman–Stanley embedding is optimal for Scott sentence complexity now follows easily from Corollary 3.9 by cardinality considerations.
Theorem 3.10. There is no Turing computable embedding
![]() $\Phi :Mod(\tau ) \to \mathrm {LO}$
such that for all
$\Phi :Mod(\tau ) \to \mathrm {LO}$
such that for all
![]() $\mathcal {A}\in Mod(\tau )$
,
$\mathcal {A}\in Mod(\tau )$
,
![]() $SSC(\mathcal {A})=\Pi ^{\mathrm {in}}_{2}$
if and only if
$SSC(\mathcal {A})=\Pi ^{\mathrm {in}}_{2}$
if and only if
![]() $SSC(\Phi (\mathcal {A}))\in \{ \Sigma ^{\mathrm {in}}_{4}, d\text{-}\Sigma ^{\mathrm {in}}_{3}, \Pi ^{\mathrm {in}}_{3}\}$
for any countable vocabulary
$SSC(\Phi (\mathcal {A}))\in \{ \Sigma ^{\mathrm {in}}_{4}, d\text{-}\Sigma ^{\mathrm {in}}_{3}, \Pi ^{\mathrm {in}}_{3}\}$
for any countable vocabulary
![]() $\tau $
.
$\tau $
.
Proof. We may assume that
![]() $\tau $
contains only one binary relation symbol, i.e., that the
$\tau $
contains only one binary relation symbol, i.e., that the
![]() $\tau $
-structures are graphs. Notice that there are continuum many graphs with Scott sentence complexity
$\tau $
-structures are graphs. Notice that there are continuum many graphs with Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{2}$
: For any
$\Pi ^{\mathrm {in}}_{2}$
: For any
![]() $X\subseteq \omega $
the graph consisting of a cycle of size
$X\subseteq \omega $
the graph consisting of a cycle of size
![]() $n+2$
for every
$n+2$
for every
![]() $n\in X$
has a
$n\in X$
has a
![]() $\Pi ^{\mathrm {in}}_{2}$
Scott sentence. To see this just notice that the automorphism orbit of any element x in a cycle of size
$\Pi ^{\mathrm {in}}_{2}$
Scott sentence. To see this just notice that the automorphism orbit of any element x in a cycle of size
![]() $c_x$
is definable by the
$c_x$
is definable by the
![]() $\Sigma ^0_1$
-formula
$\Sigma ^0_1$
-formula
 $$\begin{align*}\exists y_1,\dots, y_{c_x} \left(y_1=x \land y_{c_x}\mathbin{E} y_1 \land \bigwedge_{i<c_x} y_i\mathbin{E} y_{i+1}\right).\end{align*}$$
$$\begin{align*}\exists y_1,\dots, y_{c_x} \left(y_1=x \land y_{c_x}\mathbin{E} y_1 \land \bigwedge_{i<c_x} y_i\mathbin{E} y_{i+1}\right).\end{align*}$$
However, by Corollary 3.9 there are only countably many linear orderings with a
![]() $\Sigma ^{\mathrm {in}}_{4}$
Scott sentence. As any potential embedding
$\Sigma ^{\mathrm {in}}_{4}$
Scott sentence. As any potential embedding
![]() $\Phi $
needs to respect isomorphism, it cannot map every graph with a
$\Phi $
needs to respect isomorphism, it cannot map every graph with a
![]() $\Pi ^{\mathrm {in}}_{2}$
Scott sentence to a linear ordering with a Scott sentence of complexity in
$\Pi ^{\mathrm {in}}_{2}$
Scott sentence to a linear ordering with a Scott sentence of complexity in
![]() $\{\Sigma ^{\mathrm {in}}_{4}, d\text{-}\Sigma ^{\mathrm {in}}_{3},\Pi ^{\mathrm {in}}_{3}\}$
.
$\{\Sigma ^{\mathrm {in}}_{4}, d\text{-}\Sigma ^{\mathrm {in}}_{3},\Pi ^{\mathrm {in}}_{3}\}$
.
Proposition 3.11. There is no countable class of
![]() $4$
-universal linear orderings.
$4$
-universal linear orderings.
Proof. As mentioned in the proof of Theorem 3.10 there are uncountably many graphs with Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{2}$
. The Friedman–Stanley embedding transforms those into linear orderings of Scott sentence complexity
$\Pi ^{\mathrm {in}}_{2}$
. The Friedman–Stanley embedding transforms those into linear orderings of Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{4}$
. Thus, by Lemma 3.2 there can not be a countable
$\Pi ^{\mathrm {in}}_{4}$
. Thus, by Lemma 3.2 there can not be a countable
![]() $4$
-universal set of linear orderings.
$4$
-universal set of linear orderings.
4 Possible Scott sentence complexities of linear orderings
We now exhibit possible Scott sentence complexities of linear orderings. Many of our examples are constructed by producing shuffle sums of linear orderings.
Definition 4.1. Given a set S of countable linear orderings, the shuffle sum
![]() $Sh(S)$
of S is obtained by partitioning
$Sh(S)$
of S is obtained by partitioning
![]() $\mathbb {Q}$
into
$\mathbb {Q}$
into
![]() $|S|$
dense sets
$|S|$
dense sets
![]() $K_i$
and replacing each point in
$K_i$
and replacing each point in
![]() $K_i$
with a copy of
$K_i$
with a copy of
![]() $S_i$
.
$S_i$
.
Shuffle sums are a very common construction that allows the coding of information into linear orderings. For example, if one considers a set
![]() $A\subseteq \omega $
, we can consider it as a set of finite order types and take the shuffle sum
$A\subseteq \omega $
, we can consider it as a set of finite order types and take the shuffle sum
![]() $Sh(A)$
, effectively coding the set. For a computability theoretic analysis of the coding strength of linear orderings that quite heavily uses shuffle sums see, for example, [Reference Frolov, Kalimullin, Harizanov, Kudinov and Miller9]. The crucial feature of shuffle sums is that if we partition a shuffle sum
$Sh(A)$
, effectively coding the set. For a computability theoretic analysis of the coding strength of linear orderings that quite heavily uses shuffle sums see, for example, [Reference Frolov, Kalimullin, Harizanov, Kudinov and Miller9]. The crucial feature of shuffle sums is that if we partition a shuffle sum
![]() $Sh(S)$
into intervals
$Sh(S)$
into intervals
![]() $P_i$
that are closed under the orderings in S (the partition does not split any subordering of type
$P_i$
that are closed under the orderings in S (the partition does not split any subordering of type
![]() $S_i\in S$
), then
$S_i\in S$
), then
![]() $P_i\cong Sh(S)$
for all
$P_i\cong Sh(S)$
for all
![]() $P_i$
. This immediately follows from the fact that every
$P_i$
. This immediately follows from the fact that every
![]() $S_i$
is dense in
$S_i$
is dense in
![]() $Sh(S)$
. Note that a linear ordering of the form
$Sh(S)$
. Note that a linear ordering of the form
![]() $\mathcal {L}\cdot \mathbb {Q}$
is a special case of a shuffle sum. We begin by proving a couple of lemmas about the back-and-forth relations of shuffle sums.
$\mathcal {L}\cdot \mathbb {Q}$
is a special case of a shuffle sum. We begin by proving a couple of lemmas about the back-and-forth relations of shuffle sums.
Lemma 4.2. Let
![]() $\mathcal {A}$
be a shuffle sum and
$\mathcal {A}$
be a shuffle sum and
![]() $\mathcal {B} = \mathcal {L}\cdot \mathbb {Q}$
for some ordering
$\mathcal {B} = \mathcal {L}\cdot \mathbb {Q}$
for some ordering
![]() $\mathcal {L}$
. If
$\mathcal {L}$
. If
![]() $\mathcal {A}\leq _\alpha \mathcal {B}$
then
$\mathcal {A}\leq _\alpha \mathcal {B}$
then
![]() $\mathcal {A}+\mathcal {L}+\mathcal {B}\leq _{\alpha +2}\mathcal {A}+\mathcal {B}$
.
$\mathcal {A}+\mathcal {L}+\mathcal {B}\leq _{\alpha +2}\mathcal {A}+\mathcal {B}$
.
Proof. To show this, we describe a winning strategy for the
![]() $\exists $
-player in the
$\exists $
-player in the
![]() $\alpha +2$
-back-and-forth game. On the first turn, the
$\alpha +2$
-back-and-forth game. On the first turn, the
![]() $\exists $
-player copies the selected tuple of the
$\exists $
-player copies the selected tuple of the
![]() $\forall $
-player using an isomorphism of the initial
$\forall $
-player using an isomorphism of the initial
![]() $\mathcal {A}$
s and the final
$\mathcal {A}$
s and the final
![]() $\mathcal {B}$
s. The only possible non-isomorphic interval is the one between the smallest element of the tuple b that is in
$\mathcal {B}$
s. The only possible non-isomorphic interval is the one between the smallest element of the tuple b that is in
![]() $\mathcal {B}$
and the largest element of the tuple a that is in
$\mathcal {B}$
and the largest element of the tuple a that is in
![]() $\mathcal {A}$
. In other words, we need to show that
$\mathcal {A}$
. In other words, we need to show that
Because
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are shuffle sums,
$\mathcal {B}$
are shuffle sums,
![]() $\mathcal {A}_{>a}\cong N+\mathcal {A}$
and
$\mathcal {A}_{>a}\cong N+\mathcal {A}$
and
![]() $\mathcal {B}_{<b}\cong \mathcal {B}+K$
for some linear orderings N and K. This means that we only need to show that
$\mathcal {B}_{<b}\cong \mathcal {B}+K$
for some linear orderings N and K. This means that we only need to show that
![]() $\mathcal {A}+\mathcal {L}+\mathcal {B}\geq _{\alpha +1}\mathcal {A}+\mathcal {B}$
if we play isomorphically on N and K.
$\mathcal {A}+\mathcal {L}+\mathcal {B}\geq _{\alpha +1}\mathcal {A}+\mathcal {B}$
if we play isomorphically on N and K.
On the next turn, the
![]() $\forall $
-player plays on
$\forall $
-player plays on
![]() $\mathcal {A}+\mathcal {L}+\mathcal {B}$
, and the
$\mathcal {A}+\mathcal {L}+\mathcal {B}$
, and the
![]() $\exists $
-player responds on
$\exists $
-player responds on
![]() $\mathcal {A}+\mathcal {B}$
using an isomorphism between the initial
$\mathcal {A}+\mathcal {B}$
using an isomorphism between the initial
![]() $\mathcal {A}$
s and an isomorphism of
$\mathcal {A}$
s and an isomorphism of
![]() $\mathcal {L}+\mathcal {B}$
to a final segment of
$\mathcal {L}+\mathcal {B}$
to a final segment of
![]() $\mathcal {B}$
. Assume without loss of generality that c is the smallest element in
$\mathcal {B}$
. Assume without loss of generality that c is the smallest element in
![]() $\mathcal {L}$
played by the
$\mathcal {L}$
played by the
![]() $\forall $
-player in the distinguished copy of
$\forall $
-player in the distinguished copy of
![]() $\mathcal {L}$
within
$\mathcal {L}$
within
![]() $\mathcal {A}+\mathcal {L}+\mathcal {B}$
. The only possible non-isomorphic interval is between c and the largest element a selected within
$\mathcal {A}+\mathcal {L}+\mathcal {B}$
. The only possible non-isomorphic interval is between c and the largest element a selected within
![]() $\mathcal {A}$
. In other words, we need to show that
$\mathcal {A}$
. In other words, we need to show that
As
![]() $\mathcal {A}_{>a}\cong M+\mathcal {A}$
and the
$\mathcal {A}_{>a}\cong M+\mathcal {A}$
and the
![]() $\exists $
-player can play the isomorphism between the copies of
$\exists $
-player can play the isomorphism between the copies of
![]() $\mathcal {L}_{<c}$
and M, it is sufficient to show that
$\mathcal {L}_{<c}$
and M, it is sufficient to show that
![]() $\mathcal {A}\leq _{\alpha }\mathcal {A}+\mathcal {B}$
. As
$\mathcal {A}\leq _{\alpha }\mathcal {A}+\mathcal {B}$
. As
![]() $\mathcal {A}$
is a shuffle sum
$\mathcal {A}$
is a shuffle sum
![]() $\mathcal {A}\cong \mathcal {A}+\mathcal {A}$
. Therefore, it is enough to show that
$\mathcal {A}\cong \mathcal {A}+\mathcal {A}$
. Therefore, it is enough to show that
![]() $\mathcal {A}\leq _\alpha \mathcal {B}$
, as desired.
$\mathcal {A}\leq _\alpha \mathcal {B}$
, as desired.
Corollary 4.3. Let
![]() $\mathcal {A}$
be a shuffle sum and
$\mathcal {A}$
be a shuffle sum and
![]() $\mathcal {B} = \mathcal {L}\cdot \mathbb {Q}$
for some ordering
$\mathcal {B} = \mathcal {L}\cdot \mathbb {Q}$
for some ordering
![]() $\mathcal {L}$
. If
$\mathcal {L}$
. If
![]() $\mathcal {A}+\mathcal {L}+\mathcal {B}\not \cong \mathcal {A}+\mathcal {B}$
and
$\mathcal {A}+\mathcal {L}+\mathcal {B}\not \cong \mathcal {A}+\mathcal {B}$
and
![]() $\mathcal {A}\leq _\alpha \mathcal {B}$
, then
$\mathcal {A}\leq _\alpha \mathcal {B}$
, then
![]() $\mathcal {A}+\mathcal {L}+\mathcal {B}$
has no
$\mathcal {A}+\mathcal {L}+\mathcal {B}$
has no
![]() $\Pi ^{\mathrm {in}}_{\alpha +2}$
Scott sentence.
$\Pi ^{\mathrm {in}}_{\alpha +2}$
Scott sentence.
We are now ready to provide the constructions of example linear orderings.
Theorem 4.4. There is a linear ordering with Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{4}$
.
$\Sigma ^{\mathrm {in}}_{4}$
.
Proof. Consider the linear ordering
![]() $\mathcal {L}=2\cdot \mathbb {Q}+1+\mathbb {Q}$
and call the
$\mathcal {L}=2\cdot \mathbb {Q}+1+\mathbb {Q}$
and call the
![]() $1$
in the middle c. We claim that
$1$
in the middle c. We claim that
![]() $SR(\mathcal {L},c)=\max \{SR(2\cdot \mathbb {Q}),SR(\mathbb {Q})\}\leq 2$
(the first equality follows from [Reference Gonzalez and Montalbán14, Lemma 11]). The inequality follows from the fact that in
$SR(\mathcal {L},c)=\max \{SR(2\cdot \mathbb {Q}),SR(\mathbb {Q})\}\leq 2$
(the first equality follows from [Reference Gonzalez and Montalbán14, Lemma 11]). The inequality follows from the fact that in
![]() $2\cdot \mathbb {Q}$
the orbits of singletons are defined by the
$2\cdot \mathbb {Q}$
the orbits of singletons are defined by the
![]() $\Sigma ^{\mathrm {in}}_{2}$
-formulas
$\Sigma ^{\mathrm {in}}_{2}$
-formulas
![]() $\exists y\ S(x)=y$
and
$\exists y\ S(x)=y$
and
![]() $\exists y\ S(y)=x$
. This definition extends to tuples by adding in the order of the tuple to the definition along with any successor relations that hold.
$\exists y\ S(y)=x$
. This definition extends to tuples by adding in the order of the tuple to the definition along with any successor relations that hold.
We now show that
![]() $\mathcal {L}$
has Scott sentence complexity
$\mathcal {L}$
has Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{4}$
. This will be done by showing that it does not have a
$\Sigma ^{\mathrm {in}}_{4}$
. This will be done by showing that it does not have a
![]() $\Pi ^{\mathrm {in}}_{4}$
Scott sentence. In order to do this, we appeal to Corollary 4.3 which implies that all we need to show is that
$\Pi ^{\mathrm {in}}_{4}$
Scott sentence. In order to do this, we appeal to Corollary 4.3 which implies that all we need to show is that
![]() $2\cdot \mathbb {Q}\leq _2\mathbb {Q}$
. However, this follows immediately from the 2-universality of
$2\cdot \mathbb {Q}\leq _2\mathbb {Q}$
. However, this follows immediately from the 2-universality of
![]() $\mathbb {Q}$
among infinite linear orderings (Lemma 3.4).
$\mathbb {Q}$
among infinite linear orderings (Lemma 3.4).
Note that the above proof also implies that
![]() $2\cdot \mathbb {Q}+1+\mathbb {Q}\leq _42\cdot \mathbb {Q}+\mathbb {Q}$
.
$2\cdot \mathbb {Q}+1+\mathbb {Q}\leq _42\cdot \mathbb {Q}+\mathbb {Q}$
.
Theorem 4.5. There is a linear ordering with Scott sentence complexity
![]() $\Sigma _5^{in}$
.
$\Sigma _5^{in}$
.
Proof. Let
![]() $\mathcal {A}=Sh(\{1,\omega \})$
,
$\mathcal {A}=Sh(\{1,\omega \})$
,
![]() $\mathcal {B}=\omega \cdot \mathbb {Q}$
,
$\mathcal {B}=\omega \cdot \mathbb {Q}$
,
![]() $\mathcal {L}=\mathcal {A}+\omega +\mathcal {B}$
and denote the first element of the
$\mathcal {L}=\mathcal {A}+\omega +\mathcal {B}$
and denote the first element of the
![]() $\omega $
in the middle by c. We claim that
$\omega $
in the middle by c. We claim that
![]() $\mathcal {L}$
has Scott sentence complexity
$\mathcal {L}$
has Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{5}$
.
$\Sigma ^{\mathrm {in}}_{5}$
.
First, we show that
![]() $SR(\mathcal {L},c)=\max \{SR(\mathcal {A}),SR(\mathcal {B})\}\leq 3$
(the first equality follows from [Reference Gonzalez and Montalbán14, Lemma 11]). Define the following family of formulas that denote if x is the top of an successor chain of length
$SR(\mathcal {L},c)=\max \{SR(\mathcal {A}),SR(\mathcal {B})\}\leq 3$
(the first equality follows from [Reference Gonzalez and Montalbán14, Lemma 11]). Define the following family of formulas that denote if x is the top of an successor chain of length
![]() $n>1$
:
$n>1$
:
Note that
![]() $S_n(x)$
is
$S_n(x)$
is
![]() $\Sigma ^{\mathrm {in}}_{2}$
. It is not difficult to see that the automorphism orbits of elements in
$\Sigma ^{\mathrm {in}}_{2}$
. It is not difficult to see that the automorphism orbits of elements in
![]() $\mathcal {B}$
are given by the formulas
$\mathcal {B}$
are given by the formulas
These formulas are all
![]() $\Sigma ^{\mathrm {in}}_{3}$
and the automorphism orbits of tuples can be constructed by taking conjunctions over them along with adding any needed successor relations between the elements. Thus,
$\Sigma ^{\mathrm {in}}_{3}$
and the automorphism orbits of tuples can be constructed by taking conjunctions over them along with adding any needed successor relations between the elements. Thus,
![]() $SR(\mathcal {B})\leq 3$
. Similarly, within
$SR(\mathcal {B})\leq 3$
. Similarly, within
![]() $\mathcal {A}$
the automorphism orbits of elements are given by the formulas
$\mathcal {A}$
the automorphism orbits of elements are given by the formulas
To extend these definitions to tuples we only need to add the successor relations that hold between the elements and the order of the elements. All of these definitions are
![]() $\Sigma ^{\mathrm {in}}_{3}$
and therefore
$\Sigma ^{\mathrm {in}}_{3}$
and therefore
![]() $SR(\mathcal {A})\leq 3$
.
$SR(\mathcal {A})\leq 3$
.
It remains to show that
![]() $\mathcal {L}$
does not have a
$\mathcal {L}$
does not have a
![]() $\Pi ^{\mathrm {in}}_{5}$
Scott sentence. By Corollary 4.3 it is enough to show that
$\Pi ^{\mathrm {in}}_{5}$
Scott sentence. By Corollary 4.3 it is enough to show that
![]() $\omega \cdot \mathbb {Q}\geq _3\mathcal {A}$
. Towards this let
$\omega \cdot \mathbb {Q}\geq _3\mathcal {A}$
. Towards this let
![]() $\bar {p}\in \omega \cdot \mathbb {Q}$
be an ordered tuple. We want to find
$\bar {p}\in \omega \cdot \mathbb {Q}$
be an ordered tuple. We want to find
![]() $\bar q\in \mathcal {A}$
such that
$\bar q\in \mathcal {A}$
such that
![]() $(\omega \cdot \mathbb {Q},\bar p)\leq _2(\mathcal {A},\bar q)$
. To do this, take an ordered tuple
$(\omega \cdot \mathbb {Q},\bar p)\leq _2(\mathcal {A},\bar q)$
. To do this, take an ordered tuple
![]() $\bar {q}\in \mathcal {A}$
such that every
$\bar {q}\in \mathcal {A}$
such that every
![]() $q_i$
is in an
$q_i$
is in an
![]() $\omega $
-block and in the same position within that block as
$\omega $
-block and in the same position within that block as
![]() $p_i$
. Furthermore, assure that for each pair
$p_i$
. Furthermore, assure that for each pair
![]() $i<j$
,
$i<j$
,
![]() $p_i$
and
$p_i$
and
![]() $p_j$
are in the same
$p_j$
are in the same
![]() $\omega $
-block if and only if
$\omega $
-block if and only if
![]() $q_i$
and
$q_i$
and
![]() $q_j$
are. In particular, finite intervals formed by
$q_j$
are. In particular, finite intervals formed by
![]() $\bar p$
within an
$\bar p$
within an
![]() $\omega $
-block are isomorphic to the corresponding finite intervals formed by
$\omega $
-block are isomorphic to the corresponding finite intervals formed by
![]() $\bar q$
within an
$\bar q$
within an
![]() $\omega $
-block. Note that, for each i not accounted for in the above analysis, there is some
$\omega $
-block. Note that, for each i not accounted for in the above analysis, there is some
![]() $k_i\in \omega $
, such that
$k_i\in \omega $
, such that
![]() $(p_i,p_{i+1})\cong \omega +\mathcal {A}+k_i$
and
$(p_i,p_{i+1})\cong \omega +\mathcal {A}+k_i$
and
![]() $(q_i,q_{i+1})\cong \omega +\omega \cdot \mathbb {Q}+k_i$
. Therefore, it is enough to show that
$(q_i,q_{i+1})\cong \omega +\omega \cdot \mathbb {Q}+k_i$
. Therefore, it is enough to show that
Repeating the style of argument from above we fix a tuple
![]() $\bar {p}\in \mathcal {A}$
and find a suitable
$\bar {p}\in \mathcal {A}$
and find a suitable
![]() $\bar {q}\in \omega \cdot \mathbb {Q}$
such that
$\bar {q}\in \omega \cdot \mathbb {Q}$
such that
![]() $(\mathcal {A},\bar {p})\leq _1(\omega \cdot \mathbb {Q},\bar {q}).$
Recall that
$(\mathcal {A},\bar {p})\leq _1(\omega \cdot \mathbb {Q},\bar {q}).$
Recall that
![]() $\mathcal {A}\leq _1 \mathcal {B}$
if and only if
$\mathcal {A}\leq _1 \mathcal {B}$
if and only if
![]() $|\mathcal {B}|\leq |\mathcal {A}|$
. Assuming that
$|\mathcal {B}|\leq |\mathcal {A}|$
. Assuming that
![]() $\bar {p}$
is ordered,
$\bar {p}$
is ordered,
![]() $(p_i,p_{i+1})$
has cardinality
$(p_i,p_{i+1})$
has cardinality
![]() $n\in \omega $
or
$n\in \omega $
or
![]() $\aleph _0$
with the first and last intervals always having cardinality
$\aleph _0$
with the first and last intervals always having cardinality
![]() $\aleph _0$
. Any combination of gaps of size n and
$\aleph _0$
. Any combination of gaps of size n and
![]() $\aleph _0$
can also be found in
$\aleph _0$
can also be found in
![]() $\omega \cdot \mathbb {Q}$
and we can thus find a suitable tuple
$\omega \cdot \mathbb {Q}$
and we can thus find a suitable tuple
![]() $\bar {q}$
to finish the proof.
$\bar {q}$
to finish the proof.
Given these base case examples of linear orderings of small Scott sentence complexity, we now devise a method of systematically using these examples to fill in most of the larger Scott sentence complexities. The examples are quite simple; we consider orderings of the form
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}$
where
$\mathbb {Z}^\alpha \cdot \mathcal {L}$
where
![]() $\mathcal {L}$
is one of our previously constructed examples. The more difficult work is determining exactly of what Scott sentence complexity these orderings are.
$\mathcal {L}$
is one of our previously constructed examples. The more difficult work is determining exactly of what Scott sentence complexity these orderings are.
This will be proven by demonstrating an upper and lower bound on the complexity of the Scott sentence. We begin with proving the lower bound. In the proof of the below lemma we use
![]() $\zeta _\alpha $
to denote the unique up to isomorphism initial segment of
$\zeta _\alpha $
to denote the unique up to isomorphism initial segment of
![]() $\mathbb {Z}^\alpha $
. It is easy to check that
$\mathbb {Z}^\alpha $
. It is easy to check that
![]() $\zeta _\alpha ^*$
is the unique end segment of
$\zeta _\alpha ^*$
is the unique end segment of
![]() $\mathbb {Z}^\alpha $
and that
$\mathbb {Z}^\alpha $
and that
![]() $\zeta _{\alpha +1}^*=\zeta _\alpha +\mathbb {Z}^\alpha \cdot \omega $
.
$\zeta _{\alpha +1}^*=\zeta _\alpha +\mathbb {Z}^\alpha \cdot \omega $
.
Lemma 4.6. For the sake of organization, consider the following ordinal indexed propositions.
-
(
 $A_\alpha $
) For any
$A_\alpha $
) For any
 $\mathcal {K}$
and
$\mathcal {K}$
and
 $\mathcal {L}$
,
$\mathcal {L}$
,
 $\mathbb {Z}^\alpha \cdot \mathcal {K} \leq _{2\alpha }\mathbb {Z}^\alpha \cdot \mathcal {L}$
.
$\mathbb {Z}^\alpha \cdot \mathcal {K} \leq _{2\alpha }\mathbb {Z}^\alpha \cdot \mathcal {L}$
. -
(
 $B_\alpha $
) For any
$B_\alpha $
) For any
 $\mathcal {K}$
and
$\mathcal {K}$
and
 $\mathcal {L}$
with
$\mathcal {L}$
with
 $|\mathcal {K}|\geq |\mathcal {L}|$
,
$|\mathcal {K}|\geq |\mathcal {L}|$
,
 $\mathbb {Z}^\alpha \cdot \mathcal {K} \leq _{2\alpha +1}\mathbb {Z}^\alpha \cdot \mathcal {L}$
.
$\mathbb {Z}^\alpha \cdot \mathcal {K} \leq _{2\alpha +1}\mathbb {Z}^\alpha \cdot \mathcal {L}$
. -
(
 $C_\alpha $
) For any
$C_\alpha $
) For any
 $\mathcal {K}$
and any
$\mathcal {K}$
and any
 $\mathcal {L}$
without a last element,
$\mathcal {L}$
without a last element,
 $\mathbb {Z}^\alpha \cdot (\omega +\mathcal {K})\leq _{2\alpha +2} \mathbb {Z}^\alpha \cdot$
$\mathbb {Z}^\alpha \cdot (\omega +\mathcal {K})\leq _{2\alpha +2} \mathbb {Z}^\alpha \cdot$
 $(\omega +\mathcal {L})$
.
$(\omega +\mathcal {L})$
.
For any countable ordinal
![]() $\alpha $
,
$\alpha $
,
![]() $A_\alpha $
,
$A_\alpha $
,
![]() $B_\alpha $
, and
$B_\alpha $
, and
![]() $C_\alpha $
are true.
$C_\alpha $
are true.
Proof. The proof is by induction with the statements
![]() $A_0$
and
$A_0$
and
![]() $B_0$
trivially true. We start by showing that
$B_0$
trivially true. We start by showing that
![]() $B_\alpha $
implies
$B_\alpha $
implies
![]() $A_{\alpha +1}$
.
$A_{\alpha +1}$
.
Select a tuple
![]() $a_0\dots a_n$
in
$a_0\dots a_n$
in
![]() $\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}=\mathbb {Z}^\alpha \cdot \mathbb {Z}\cdot \mathcal {L}$
. We will find a tuple
$\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}=\mathbb {Z}^\alpha \cdot \mathbb {Z}\cdot \mathcal {L}$
. We will find a tuple
![]() $b_0\dots b_n$
in
$b_0\dots b_n$
in
![]() $\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}=\mathbb {Z}^\alpha \cdot \mathbb {Z}\cdot \mathcal {K}$
such that
$\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}=\mathbb {Z}^\alpha \cdot \mathbb {Z}\cdot \mathcal {K}$
such that
![]() $(\mathbb {Z}^{\alpha +1}\cdot \mathcal {L},\bar a )\leq _{2\alpha +1} (\mathbb {Z}^{\alpha +1}\cdot \mathcal {K},\bar b)$
. Pick a point
$(\mathbb {Z}^{\alpha +1}\cdot \mathcal {L},\bar a )\leq _{2\alpha +1} (\mathbb {Z}^{\alpha +1}\cdot \mathcal {K},\bar b)$
. Pick a point
![]() $b_0$
arbitrarily. Given
$b_0$
arbitrarily. Given
![]() $b_j$
, we pick
$b_j$
, we pick
![]() $b_{j+1}$
as follows. If
$b_{j+1}$
as follows. If
![]() $a_j$
and
$a_j$
and
![]() $a_{j+1}$
are in the same copy of
$a_{j+1}$
are in the same copy of
![]() $\mathbb {Z}^{\alpha +1}$
, we can pick
$\mathbb {Z}^{\alpha +1}$
, we can pick
![]() $b_{j+1}$
such that
$b_{j+1}$
such that
![]() $(a_j,a_{j+1})\cong (b_j,b_{j+1})$
. If not, we pick
$(a_j,a_{j+1})\cong (b_j,b_{j+1})$
. If not, we pick
![]() $b_{j+1}$
arbitrarily in the copy of
$b_{j+1}$
arbitrarily in the copy of
![]() $\mathbb {Z}^{\alpha }$
that is the successor of the successor of the copy of
$\mathbb {Z}^{\alpha }$
that is the successor of the successor of the copy of
![]() $\mathbb {Z}^{\alpha }$
containing
$\mathbb {Z}^{\alpha }$
containing
![]() $b_j$
. In other words, we pick
$b_j$
. In other words, we pick
![]() $b_{j+1}$
with
$b_{j+1}$
with
![]() $(b_j,b_{j+1})\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha +\zeta _\alpha $
.
$(b_j,b_{j+1})\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha +\zeta _\alpha $
.
To show that our choice of
![]() $\bar b$
is correct, we have to confirm the following relations between non-isomorphic intervals.
$\bar b$
is correct, we have to confirm the following relations between non-isomorphic intervals.
-
(1)
 $(b_j,b_{j+1})\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha +\zeta _\alpha \geq _{2\alpha +1} \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {L}_1+\zeta _\alpha $
, where
$(b_j,b_{j+1})\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha +\zeta _\alpha \geq _{2\alpha +1} \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {L}_1+\zeta _\alpha $
, where
 $\mathcal {L}_1$
is an infinite order,
$\mathcal {L}_1$
is an infinite order, -
(2)
 $(-\infty ,b_0)\cong \mathbb {Z}^\alpha \cdot \mathcal {K}_1+\zeta _\alpha \geq _{2\alpha +1}\mathbb {Z}^\alpha \cdot \mathcal {L}_1+\zeta _\alpha $
, where
$(-\infty ,b_0)\cong \mathbb {Z}^\alpha \cdot \mathcal {K}_1+\zeta _\alpha \geq _{2\alpha +1}\mathbb {Z}^\alpha \cdot \mathcal {L}_1+\zeta _\alpha $
, where
 $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
 $\mathcal {K}_1$
are some initial segments of
$\mathcal {K}_1$
are some initial segments of
 $\mathbb {Z}\cdot \mathcal {L}$
and
$\mathbb {Z}\cdot \mathcal {L}$
and
 $\mathbb {Z}\cdot \mathcal {K}$
, and therefore infinite, or
$\mathbb {Z}\cdot \mathcal {K}$
, and therefore infinite, or -
(3)
 $(b_{n},\infty )\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {L}_1 \geq _{2\alpha +1} \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {K}_1$
, where
$(b_{n},\infty )\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {L}_1 \geq _{2\alpha +1} \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {K}_1$
, where
 $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
 $\mathcal {K}_1$
are some final segments of
$\mathcal {K}_1$
are some final segments of
 $\mathbb {Z}\cdot \mathcal {L}$
and
$\mathbb {Z}\cdot \mathcal {L}$
and
 $\mathbb {Z}\cdot \mathcal {K}$
, and therefore infinite.
$\mathbb {Z}\cdot \mathcal {K}$
, and therefore infinite.
It follows immediately from
![]() $B_\alpha $
that all of these back-and-forth relations hold.
$B_\alpha $
that all of these back-and-forth relations hold.
We now show that
![]() $B_\alpha $
implies
$B_\alpha $
implies
![]() $C_\alpha $
. So assume that
$C_\alpha $
. So assume that
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $\mathcal {L}$
have no last element and that
$\mathcal {L}$
have no last element and that
![]() $B_\alpha $
holds. Select a tuple
$B_\alpha $
holds. Select a tuple
![]() $a_0\dots a_n$
in
$a_0\dots a_n$
in
![]() $\mathbb {Z}^\alpha \cdot (\omega +\mathcal {L})$
. Without loss of generality,
$\mathbb {Z}^\alpha \cdot (\omega +\mathcal {L})$
. Without loss of generality,
![]() $a_0$
is in the first copy of
$a_0$
is in the first copy of
![]() $\mathbb {Z}^\alpha $
. We will find a tuple
$\mathbb {Z}^\alpha $
. We will find a tuple
![]() $b_0\dots b_n$
in
$b_0\dots b_n$
in
![]() $\mathbb {Z}^\alpha \cdot (\omega +\mathcal {K})$
such that
$\mathbb {Z}^\alpha \cdot (\omega +\mathcal {K})$
such that
![]() $(\mathbb {Z}^\alpha \cdot (\omega +\mathcal {L}),\bar a)\leq _{2\alpha +1} (\mathbb {Z}^\alpha \cdot (\omega +\mathcal {K}),\bar b)$
. For the
$(\mathbb {Z}^\alpha \cdot (\omega +\mathcal {L}),\bar a)\leq _{2\alpha +1} (\mathbb {Z}^\alpha \cdot (\omega +\mathcal {K}),\bar b)$
. For the
![]() $a_j$
in the initial
$a_j$
in the initial
![]() $\mathbb {Z}^\alpha \cdot \omega $
, the
$\mathbb {Z}^\alpha \cdot \omega $
, the
![]() $b_j$
are picked isomorphically. We now define the rest of the
$b_j$
are picked isomorphically. We now define the rest of the
![]() $b_j$
by induction so that all of them are in the initial
$b_j$
by induction so that all of them are in the initial
![]() $\mathbb {Z}^\alpha \cdot \omega $
. If
$\mathbb {Z}^\alpha \cdot \omega $
. If
![]() $a_j$
is in the same
$a_j$
is in the same
![]() $\mathbb {Z}^\alpha $
block as
$\mathbb {Z}^\alpha $
block as
![]() $a_{j+1}$
or
$a_{j+1}$
or
![]() $a_{j+1}$
is in the successor of
$a_{j+1}$
is in the successor of
![]() $a_j$
’s block, define
$a_j$
’s block, define
![]() $b_{j+1}$
so that
$b_{j+1}$
so that
![]() $(b_j,b_{j+1})\cong (a_j,a_{j+1})$
. Otherwise, define
$(b_j,b_{j+1})\cong (a_j,a_{j+1})$
. Otherwise, define
![]() $b_{j+1}$
as being some element in the successor of the successor of the
$b_{j+1}$
as being some element in the successor of the successor of the
![]() $\mathbb {Z}^\alpha $
block containing
$\mathbb {Z}^\alpha $
block containing
![]() $b_j$
. Not including isomorphic intervals, we only need to check the following cases.
$b_j$
. Not including isomorphic intervals, we only need to check the following cases.
-
(1)
 $(b_j,b_{j+1})\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha +\zeta _\alpha \geq _{2\alpha +1} \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {L}_1+\zeta _\alpha $
where
$(b_j,b_{j+1})\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha +\zeta _\alpha \geq _{2\alpha +1} \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {L}_1+\zeta _\alpha $
where
 $\mathcal {L}_1$
is infinite,
$\mathcal {L}_1$
is infinite, -
(2)
 $(b_n,\infty )\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot (\omega +\mathcal {K}) \geq _{2\alpha +1} \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {L}_1$
, where
$(b_n,\infty )\cong \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot (\omega +\mathcal {K}) \geq _{2\alpha +1} \zeta ^*_\alpha +\mathbb {Z}^\alpha \cdot \mathcal {L}_1$
, where
 $\mathcal {L}_1$
is some final segment of
$\mathcal {L}_1$
is some final segment of
 $\omega +\mathcal {L}$
, and thus infinite.
$\omega +\mathcal {L}$
, and thus infinite.
All of these relations follow from
![]() $B_\alpha $
, as desired.
$B_\alpha $
, as desired.
To complete the proof of the successor step of the induction, we show that
![]() $C_\alpha $
and
$C_\alpha $
and
![]() $A_{\alpha +1}$
imply
$A_{\alpha +1}$
imply
![]() $B_{\alpha +1}$
.
$B_{\alpha +1}$
.
Select a tuple
![]() $a_0\dots a_n$
in
$a_0\dots a_n$
in
![]() $\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}$
. These points belong to at most n distinct copies of
$\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}$
. These points belong to at most n distinct copies of
![]() $\mathbb {Z}^{\alpha +1}$
. Because
$\mathbb {Z}^{\alpha +1}$
. Because
![]() $|\mathcal {K}|\geq | \mathcal {L}|$
, we can match each chosen copy of
$|\mathcal {K}|\geq | \mathcal {L}|$
, we can match each chosen copy of
![]() $\mathbb {Z}^{\alpha +1}$
to one in
$\mathbb {Z}^{\alpha +1}$
to one in
![]() $\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}$
. Furthermore, if there is a copy of
$\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}$
. Furthermore, if there is a copy of
![]() $\mathbb {Z}^{\alpha +1}$
between two of the chosen copies in
$\mathbb {Z}^{\alpha +1}$
between two of the chosen copies in
![]() $\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}$
, we can assure that the corresponding copies in
$\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}$
, we can assure that the corresponding copies in
![]() $\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}$
are also not successors. Also, if
$\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}$
are also not successors. Also, if
![]() $a_n$
is not in the last copy of
$a_n$
is not in the last copy of
![]() $\mathbb {Z}^{\alpha +1}$
, we can assure that neither is
$\mathbb {Z}^{\alpha +1}$
, we can assure that neither is
![]() $b_n$
and, similarly for
$b_n$
and, similarly for
![]() $a_0$
and
$a_0$
and
![]() $b_0$
in the first copy. In particular, not including the isomorphic intervals, we only need to check the following cases.
$b_0$
in the first copy. In particular, not including the isomorphic intervals, we only need to check the following cases.
-
(1)
 $(b_j,b_{j+1})\hspace{-0.5pt}\cong\hspace{-0.5pt} \zeta ^*_{\alpha +1} +\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}_1\hspace{-0.5pt}+\hspace{-0.5pt}\zeta _{\alpha +1}\geq _{2\alpha +2}\zeta ^*_{\alpha +1}\hspace{-0.5pt} +\hspace{-0.5pt}\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}_1\hspace{-0.5pt}+\hspace{-0.5pt}\zeta _{\alpha +1}$
for some orderings
$(b_j,b_{j+1})\hspace{-0.5pt}\cong\hspace{-0.5pt} \zeta ^*_{\alpha +1} +\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}_1\hspace{-0.5pt}+\hspace{-0.5pt}\zeta _{\alpha +1}\geq _{2\alpha +2}\zeta ^*_{\alpha +1}\hspace{-0.5pt} +\hspace{-0.5pt}\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}_1\hspace{-0.5pt}+\hspace{-0.5pt}\zeta _{\alpha +1}$
for some orderings
 $\mathcal {K}_1$
and
$\mathcal {K}_1$
and
 $\mathcal {L}_1$
,
$\mathcal {L}_1$
, -
(2)
 $(b_n,\infty )\cong \zeta ^*_{\alpha +1} +\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}_1\geq _{2\alpha +2}\zeta ^*_{\alpha +1} +\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}_1$
for some orderings
$(b_n,\infty )\cong \zeta ^*_{\alpha +1} +\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}_1\geq _{2\alpha +2}\zeta ^*_{\alpha +1} +\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}_1$
for some orderings
 $\mathcal {K}_1$
and
$\mathcal {K}_1$
and
 $\mathcal {L}_1$
,
$\mathcal {L}_1$
, -
(3)
 $(-\infty ,b_0)\cong \mathbb {Z}^{\alpha +1}\cdot \mathcal {K}_1+\zeta _{\alpha +1}\geq _{2\alpha +2}\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}_1+\zeta _{\alpha +1}$
for some orderings
$(-\infty ,b_0)\cong \mathbb {Z}^{\alpha +1}\cdot \mathcal {K}_1+\zeta _{\alpha +1}\geq _{2\alpha +2}\mathbb {Z}^{\alpha +1}\cdot \mathcal {L}_1+\zeta _{\alpha +1}$
for some orderings
 $\mathcal {K}_1$
and
$\mathcal {K}_1$
and
 $\mathcal {L}_1$
,
$\mathcal {L}_1$
, -
(4)
 $(-\infty ,b_0)\cong \zeta _{\alpha +1}\geq _{2\alpha +2} \mathbb {Z}^{\alpha +1}\cdot \mathcal {L}_1+\zeta _{\alpha +1}$
for some order
$(-\infty ,b_0)\cong \zeta _{\alpha +1}\geq _{2\alpha +2} \mathbb {Z}^{\alpha +1}\cdot \mathcal {L}_1+\zeta _{\alpha +1}$
for some order
 $\mathcal {L}_1$
,
$\mathcal {L}_1$
, -
(5)
 $(b_n,\infty )\cong \zeta ^*_{\alpha +1} +\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}_1\geq _{2\alpha +2} \zeta ^*_{\alpha +1} $
for some order
$(b_n,\infty )\cong \zeta ^*_{\alpha +1} +\mathbb {Z}^{\alpha +1}\cdot \mathcal {K}_1\geq _{2\alpha +2} \zeta ^*_{\alpha +1} $
for some order
 $\mathcal {K}_1$
.
$\mathcal {K}_1$
.
The first three cases are handled immediately by
![]() $A_{\alpha +1}$
. By symmetry it is sufficient to show case (5). However, this is the same as showing that
$A_{\alpha +1}$
. By symmetry it is sufficient to show case (5). However, this is the same as showing that
This follows directly from
![]() $C_\alpha $
.
$C_\alpha $
.
At last we consider the remaining limit levels. We already have seen that
![]() $B_\lambda $
implies
$B_\lambda $
implies
![]() $C_\lambda $
. The statement
$C_\lambda $
. The statement
![]() $A_\lambda $
follows immediately from
$A_\lambda $
follows immediately from
![]() $A_\gamma $
for
$A_\gamma $
for
![]() $\gamma <\lambda $
. A bit more nuanced is the issue of
$\gamma <\lambda $
. A bit more nuanced is the issue of
![]() $B_\lambda $
. It follows from
$B_\lambda $
. It follows from
![]() $A_\lambda $
and
$A_\lambda $
and
![]() $C_\gamma $
for
$C_\gamma $
for
![]() $\gamma <\lambda $
. Analogous to the proof in the successor case, we analyze the possibilities:
$\gamma <\lambda $
. Analogous to the proof in the successor case, we analyze the possibilities:
-
(1)
 $\zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1+\zeta _{\lambda }\geq _\lambda \zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {L}_1+\zeta _{\lambda } $
for some orderings
$\zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1+\zeta _{\lambda }\geq _\lambda \zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {L}_1+\zeta _{\lambda } $
for some orderings
 $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
 $\mathcal {K}_1$
,
$\mathcal {K}_1$
, -
(2)
 $\zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1\geq _\lambda \zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {L}_1 $
for some orderings
$\zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1\geq _\lambda \zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {L}_1 $
for some orderings
 $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
 $\mathcal {K}_1$
,
$\mathcal {K}_1$
, -
(3)
 $\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1+\zeta _{\lambda }\geq _\lambda \mathbb {Z}^{\lambda }\cdot \mathcal {L}_1+\zeta _{\lambda } $
for some orderings
$\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1+\zeta _{\lambda }\geq _\lambda \mathbb {Z}^{\lambda }\cdot \mathcal {L}_1+\zeta _{\lambda } $
for some orderings
 $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
 $\mathcal {K}_1$
,
$\mathcal {K}_1$
, -
(4)
 $\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1+\zeta _{\lambda }\geq _\lambda \zeta _{\lambda } $
for some order
$\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1+\zeta _{\lambda }\geq _\lambda \zeta _{\lambda } $
for some order
 $\mathcal {K}_1$
,
$\mathcal {K}_1$
, -
(5)
 $\zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1\geq _\lambda \zeta ^*_{\lambda } $
for some order
$\zeta ^*_{\lambda } +\mathbb {Z}^{\lambda }\cdot \mathcal {K}_1\geq _\lambda \zeta ^*_{\lambda } $
for some order
 $\mathcal {K}_1$
.
$\mathcal {K}_1$
.
The first three cases are handled immediately by
![]() $A_{\lambda }$
. By symmetry it is clear that it is enough to show case 5. However, this is the same as showing that for all
$A_{\lambda }$
. By symmetry it is clear that it is enough to show case 5. However, this is the same as showing that for all
![]() $\gamma <\lambda $
,
$\gamma <\lambda $
,
which follows from the
![]() $C_\gamma $
for
$C_\gamma $
for
![]() $\gamma <\lambda $
.
$\gamma <\lambda $
.
Therefore, for any countable ordinal
![]() $\alpha $
,
$\alpha $
,
![]() $A_\alpha $
,
$A_\alpha $
,
![]() $B_\alpha $
, and
$B_\alpha $
, and
![]() $C_\alpha $
all hold.
$C_\alpha $
all hold.
The proposition
![]() $B_\alpha $
is analogous to Lemma II.38 in [Reference Montalbán22]. However, it has the notable advantage of being more universal, cleaner to state and easier to apply for our purposes. It is also independently interesting as it furthers our understanding of the behavior of powers of
$B_\alpha $
is analogous to Lemma II.38 in [Reference Montalbán22]. However, it has the notable advantage of being more universal, cleaner to state and easier to apply for our purposes. It is also independently interesting as it furthers our understanding of the behavior of powers of
![]() $\mathbb {Z}$
, which have been studied in [Reference Goncharov, Harizanov, Knight, McCoy, Miller and Solomon13] and [Reference Ash6]. For our purpose, what is important is that the proposition
$\mathbb {Z}$
, which have been studied in [Reference Goncharov, Harizanov, Knight, McCoy, Miller and Solomon13] and [Reference Ash6]. For our purpose, what is important is that the proposition
![]() $B_\alpha $
serves as the base case for the following lemma, which generalizes Lemmas 7.2 and 7.3 from [Reference Goncharov, Harizanov, Knight, McCoy, Miller and Solomon13] and Proposition 4.8 from [Reference Ash6].
$B_\alpha $
serves as the base case for the following lemma, which generalizes Lemmas 7.2 and 7.3 from [Reference Goncharov, Harizanov, Knight, McCoy, Miller and Solomon13] and Proposition 4.8 from [Reference Ash6].
Lemma 4.7. For any
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {K}$
$\mathcal {K}$
![]() $\mathcal {L}\leq _\beta \mathcal {K}\implies \mathbb {Z}^\alpha \cdot \mathcal {L}\leq _{2\alpha +\beta } \mathbb {Z}^\alpha \cdot \mathcal {K}.$
$\mathcal {L}\leq _\beta \mathcal {K}\implies \mathbb {Z}^\alpha \cdot \mathcal {L}\leq _{2\alpha +\beta } \mathbb {Z}^\alpha \cdot \mathcal {K}.$
Proof. We demonstrate this by induction on
![]() $\beta $
. Notice that the base case is given by the above lemma. The limit case follows immediately by the definition of the back-and-forth relations along with the observation that for any linear ordering
$\beta $
. Notice that the base case is given by the above lemma. The limit case follows immediately by the definition of the back-and-forth relations along with the observation that for any linear ordering
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() $\mathcal {L}\leq _\beta \mathcal {K} \implies \mathcal {N}\cdot \mathcal {L}\leq _\beta \mathcal {N}\cdot \mathcal {K}$
. Thus, we need only look at the successor case.
$\mathcal {L}\leq _\beta \mathcal {K} \implies \mathcal {N}\cdot \mathcal {L}\leq _\beta \mathcal {N}\cdot \mathcal {K}$
. Thus, we need only look at the successor case.
Let
![]() $\beta =\gamma +1$
and assume
$\beta =\gamma +1$
and assume
![]() $\mathcal {L}\leq _{\gamma +1} \mathcal {K}$
. We need to show that
$\mathcal {L}\leq _{\gamma +1} \mathcal {K}$
. We need to show that
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}\leq _{2\alpha +\gamma +1}\mathbb {Z}^\alpha \cdot \mathcal {K}.$
We view
$\mathbb {Z}^\alpha \cdot \mathcal {L}\leq _{2\alpha +\gamma +1}\mathbb {Z}^\alpha \cdot \mathcal {K}.$
We view
![]() $\mathbb {Z}^{\alpha }\cdot K$
as a product ordering with elements of the form
$\mathbb {Z}^{\alpha }\cdot K$
as a product ordering with elements of the form
![]() $(\delta ,b)$
where
$(\delta ,b)$
where
![]() $b\in K$
and
$b\in K$
and
![]() $\delta \in \mathbb {Z}^{\alpha }$
. Consider a play of the game where the
$\delta \in \mathbb {Z}^{\alpha }$
. Consider a play of the game where the
![]() $\forall $
-player plays a tuple
$\forall $
-player plays a tuple
![]() $(\delta _i,b_i)_{i\in k}$
from
$(\delta _i,b_i)_{i\in k}$
from
![]() $\mathbb {Z}^\alpha \cdot \mathcal {K}$
. If s is a winning strategy for demonstrating that
$\mathbb {Z}^\alpha \cdot \mathcal {K}$
. If s is a winning strategy for demonstrating that
![]() $\mathcal {L}\leq _{\gamma +1} \mathcal {K}$
, the
$\mathcal {L}\leq _{\gamma +1} \mathcal {K}$
, the
![]() $\exists $
-player may play
$\exists $
-player may play
![]() $(\delta _i,s(b_i))_{i\in k}$
in response. Let
$(\delta _i,s(b_i))_{i\in k}$
in response. Let
![]() $b_{-1}=s(b_{-1})=-\infty $
and
$b_{-1}=s(b_{-1})=-\infty $
and
![]() $b_k=s(b_k)=\infty $
by convention. We need only show that
$b_k=s(b_k)=\infty $
by convention. We need only show that
Note that the left-hand side is isomorphic to
![]() $\zeta _\alpha +\mathbb {Z}^\alpha \cdot (b_i,b_{i+1})+\zeta _\alpha ^*$
and the right-hand side is isomorphic to
$\zeta _\alpha +\mathbb {Z}^\alpha \cdot (b_i,b_{i+1})+\zeta _\alpha ^*$
and the right-hand side is isomorphic to
![]() $\zeta _\alpha +\mathbb {Z}^\alpha \cdot (s(b_i),s(b_{i+1}))+\zeta _\alpha ^*$
. As s is a winning strategy, by induction,
$\zeta _\alpha +\mathbb {Z}^\alpha \cdot (s(b_i),s(b_{i+1}))+\zeta _\alpha ^*$
. As s is a winning strategy, by induction,
which demonstrates the claim.
The following corollary follows immediately from Lemma 4.7 and the fact that multiplying by
![]() $\mathbb {Z}^\alpha $
is an injective map on linear orderings.
$\mathbb {Z}^\alpha $
is an injective map on linear orderings.
Corollary 4.8. For any linear ordering
![]() $\mathcal {L}$
, if there is a
$\mathcal {L}$
, if there is a
![]() $\mathcal {K}$
with
$\mathcal {K}$
with
![]() $\mathcal {L}\leq _\beta \mathcal {K}$
yet
$\mathcal {L}\leq _\beta \mathcal {K}$
yet
![]() $\mathcal {L}\not \cong \mathcal {K}$
then
$\mathcal {L}\not \cong \mathcal {K}$
then
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}$
has no
$\mathbb {Z}^\alpha \cdot \mathcal {L}$
has no
![]() $\Pi ^{\mathrm {in}}_{2\alpha +\beta }$
Scott sentence. For any linear ordering
$\Pi ^{\mathrm {in}}_{2\alpha +\beta }$
Scott sentence. For any linear ordering
![]() $\mathcal {L}$
, if there is a
$\mathcal {L}$
, if there is a
![]() $\mathcal {K}$
with
$\mathcal {K}$
with
![]() $\mathcal {L}\geq _\beta \mathcal {K}$
yet
$\mathcal {L}\geq _\beta \mathcal {K}$
yet
![]() $\mathcal {L}\not \cong \mathcal {K}$
then
$\mathcal {L}\not \cong \mathcal {K}$
then
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}$
has no
$\mathbb {Z}^\alpha \cdot \mathcal {L}$
has no
![]() $\Sigma ^{\mathrm {in}}_{2\alpha +\beta }$
Scott sentence.
$\Sigma ^{\mathrm {in}}_{2\alpha +\beta }$
Scott sentence.
This allows to transfer lower bounds for the Scott sentence complexity of
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}$
.
$\mathbb {Z}^\alpha \cdot \mathcal {L}$
.
We now move to proving the upper bound. In particular, we must demonstrate that multiplying by a power of
![]() $\mathbb {Z}$
does not make the Scott rank too high. For this we use the notion of the block relation
$\mathbb {Z}$
does not make the Scott rank too high. For this we use the notion of the block relation
![]() $\sim _\alpha $
. We follow the definitions in [Reference Alvir and Rossegger3].
$\sim _\alpha $
. We follow the definitions in [Reference Alvir and Rossegger3].
Lemma 4.9. If
![]() $\mathcal {L}$
has a
$\mathcal {L}$
has a
![]() $\Gamma ^{\mathrm {in}}_{\beta }$
Scott sentence for
$\Gamma ^{\mathrm {in}}_{\beta }$
Scott sentence for
![]() $\Gamma \in \{\Sigma ,\Pi ,d\text {-}\Sigma \}$
, then the linear ordering
$\Gamma \in \{\Sigma ,\Pi ,d\text {-}\Sigma \}$
, then the linear ordering
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}$
has a
$\mathbb {Z}^\alpha \cdot \mathcal {L}$
has a
![]() $\Gamma ^{\mathrm {in}}_{2\alpha +\beta }$
Scott sentence.
$\Gamma ^{\mathrm {in}}_{2\alpha +\beta }$
Scott sentence.
Proof. Given a formula
![]() $\varphi $
in the language of linear orderings we define
$\varphi $
in the language of linear orderings we define
![]() $\varphi _\alpha $
as being the same as
$\varphi _\alpha $
as being the same as
![]() $\varphi $
except for the fact that instances of
$\varphi $
except for the fact that instances of
![]() $x<y$
are replaced by
$x<y$
are replaced by
![]() $x<y \land x\not \sim _\alpha y$
and instances of
$x<y \land x\not \sim _\alpha y$
and instances of
![]() $x=y$
are replaced by
$x=y$
are replaced by
![]() $x\sim _\alpha y$
. Note that if
$x\sim _\alpha y$
. Note that if
![]() $\varphi $
is
$\varphi $
is
![]() $\Gamma ^{\mathrm {in}}_{\beta }$
, then
$\Gamma ^{\mathrm {in}}_{\beta }$
, then
![]() $\varphi _\alpha $
is at worst
$\varphi _\alpha $
is at worst
![]() $\Gamma ^{\mathrm {in}}_{2\alpha +\beta }$
by the fact that
$\Gamma ^{\mathrm {in}}_{2\alpha +\beta }$
by the fact that
![]() $\sim _\alpha $
is
$\sim _\alpha $
is
![]() $\Sigma ^{\mathrm {in}}_{2\alpha }$
definable (see [Reference Alvir and Rossegger3, Proposition 4]). It is also not difficult to see that if
$\Sigma ^{\mathrm {in}}_{2\alpha }$
definable (see [Reference Alvir and Rossegger3, Proposition 4]). It is also not difficult to see that if
![]() $\varphi $
is a Scott sentence for
$\varphi $
is a Scott sentence for
![]() $\mathcal {L}$
, then
$\mathcal {L}$
, then
![]() $\mathcal {N}\models \varphi _\alpha $
guarantees that
$\mathcal {N}\models \varphi _\alpha $
guarantees that
![]() $\mathcal {N}{/}{\sim _\alpha }\cong \mathcal {L}$
. Finally, we define
$\mathcal {N}{/}{\sim _\alpha }\cong \mathcal {L}$
. Finally, we define
Here,
![]() $S_\delta ^n(x)=y$
is shorthand for saying that y is the nth
$S_\delta ^n(x)=y$
is shorthand for saying that y is the nth
![]() $\delta $
-successor of x. In other words,
$\delta $
-successor of x. In other words,
Overall, this is
![]() $\Sigma ^{\mathrm {in}}_{2\delta +2}$
. This gives that
$\Sigma ^{\mathrm {in}}_{2\delta +2}$
. This gives that
![]() $\psi $
is, at worst,
$\psi $
is, at worst,
![]() $\Pi ^{\mathrm {in}}_{2\alpha +1}$
. Furthermore,
$\Pi ^{\mathrm {in}}_{2\alpha +1}$
. Furthermore,
![]() $\psi $
guarantees that every
$\psi $
guarantees that every
![]() $\sim _\alpha $
equivalence class is isomorphic to
$\sim _\alpha $
equivalence class is isomorphic to
![]() $\mathbb {Z}^\alpha $
. Therefore,
$\mathbb {Z}^\alpha $
. Therefore,
![]() $\varphi _\alpha \land \psi $
gives the desired Scott sentence for
$\varphi _\alpha \land \psi $
gives the desired Scott sentence for
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}$
.
$\mathbb {Z}^\alpha \cdot \mathcal {L}$
.
This result along with the previous constructions gives that there are linear orderings with any Scott sentence complexity that is not too close to a limit ordinal.
Corollary 4.10. There are linear orderings of the following Scott sentence complexities:
-
(1)
 $\Sigma ^{\mathrm {in}}_{\alpha +n}$
for any countable ordinal
$\Sigma ^{\mathrm {in}}_{\alpha +n}$
for any countable ordinal
 $\alpha $
and
$\alpha $
and
 $n\geq 4$
,
$n\geq 4$
, -
(2)
 $d\text{-}\Sigma ^{\mathrm {in}}_{\alpha +n}$
for any countable ordinal
$d\text{-}\Sigma ^{\mathrm {in}}_{\alpha +n}$
for any countable ordinal
 $\alpha $
and
$\alpha $
and
 $n\geq 1$
,
$n\geq 1$
, -
(3)
 $\Pi ^{\mathrm {in}}_{\alpha +n}$
for any countable ordinal
$\Pi ^{\mathrm {in}}_{\alpha +n}$
for any countable ordinal
 $\alpha $
and
$\alpha $
and
 $n\geq 1$
.
$n\geq 1$
.
Proof. Let
![]() $\mathcal {L}_4$
be the constructed example of Scott sentence complexity
$\mathcal {L}_4$
be the constructed example of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{4}$
and
$\Sigma ^{\mathrm {in}}_{4}$
and
![]() $\mathcal {K}_4$
such that
$\mathcal {K}_4$
such that
![]() $\mathcal {L}_4\leq _4 \mathcal {K}_4$
. Similarly define
$\mathcal {L}_4\leq _4 \mathcal {K}_4$
. Similarly define
![]() $\mathcal {L}_5$
and
$\mathcal {L}_5$
and
![]() $\mathcal {K}_5$
. For any
$\mathcal {K}_5$
. For any
![]() $\alpha $
we know that
$\alpha $
we know that
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}_4$
has a
$\mathbb {Z}^\alpha \cdot \mathcal {L}_4$
has a
![]() $\Sigma ^{\mathrm {in}}_{2\alpha +4}$
Scott sentence, yet it has no
$\Sigma ^{\mathrm {in}}_{2\alpha +4}$
Scott sentence, yet it has no
![]() $\Pi ^{\mathrm {in}}_{2\alpha +4}$
Scott sentence as
$\Pi ^{\mathrm {in}}_{2\alpha +4}$
Scott sentence as
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}_4\leq _{2\alpha +4} \mathbb {Z}^\alpha \cdot \mathcal {K}_4$
. Thus,
$\mathbb {Z}^\alpha \cdot \mathcal {L}_4\leq _{2\alpha +4} \mathbb {Z}^\alpha \cdot \mathcal {K}_4$
. Thus,
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}_4$
has Scott sentence complexity
$\mathbb {Z}^\alpha \cdot \mathcal {L}_4$
has Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{2\alpha +4}$
. Similarly,
$\Sigma ^{\mathrm {in}}_{2\alpha +4}$
. Similarly,
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}_5$
has Scott sentence complexity
$\mathbb {Z}^\alpha \cdot \mathcal {L}_5$
has Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{2\alpha +5}$
. These constructions provide examples for all of the claimed cases of the form
$\Sigma ^{\mathrm {in}}_{2\alpha +5}$
. These constructions provide examples for all of the claimed cases of the form
![]() $\Sigma ^{\mathrm {in}}_{\alpha +n}$
.
$\Sigma ^{\mathrm {in}}_{\alpha +n}$
.
Let
![]() $\mathcal {L}_2:=\mathbb {Q}+2+\mathbb {Q}$
. It is not difficult to see that this order has a
$\mathcal {L}_2:=\mathbb {Q}+2+\mathbb {Q}$
. It is not difficult to see that this order has a
![]() $d\text{-}\Sigma ^{\mathrm {in}}_{2}$
Scott sentence and that
$d\text{-}\Sigma ^{\mathrm {in}}_{2}$
Scott sentence and that
![]() $\mathbb {Q}+3+\mathbb {Q}\leq _2 \mathcal {L}_2\leq _2 \mathbb {Q}$
, so this is indeed optimal. Using the same reasoning as above, we see that
$\mathbb {Q}+3+\mathbb {Q}\leq _2 \mathcal {L}_2\leq _2 \mathbb {Q}$
, so this is indeed optimal. Using the same reasoning as above, we see that
![]() $\mathbb {Z}^\alpha \cdot \mathcal {L}_2$
has Scott sentence complexity
$\mathbb {Z}^\alpha \cdot \mathcal {L}_2$
has Scott sentence complexity
![]() $d\text{-}\Sigma ^{\mathrm {in}}_{2\alpha +2}$
. Ash [Reference Ash5] analyzed the back-and-forth relations of well-orderings and it follows from his results that
$d\text{-}\Sigma ^{\mathrm {in}}_{2\alpha +2}$
. Ash [Reference Ash5] analyzed the back-and-forth relations of well-orderings and it follows from his results that
![]() $\omega ^\alpha \cdot 2$
has Scott sentence complexity
$\omega ^\alpha \cdot 2$
has Scott sentence complexity
![]() $d\text{-}\Sigma ^{\mathrm {in}}_{2\alpha +1}$
(see [Reference Alvir and Rossegger3, proof of Proposition 19]). These constructions provide examples for all of the claimed cases of the form
$d\text{-}\Sigma ^{\mathrm {in}}_{2\alpha +1}$
(see [Reference Alvir and Rossegger3, proof of Proposition 19]). These constructions provide examples for all of the claimed cases of the form
![]() $d\text{-}\Sigma ^{\mathrm {in}}_{\alpha +n}$
.
$d\text{-}\Sigma ^{\mathrm {in}}_{\alpha +n}$
.
It is a basic exercise to show that
![]() $\mathbb {Q}$
has Scott sentence complexity
$\mathbb {Q}$
has Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{2}$
. Using the same reasoning as above, we see that
$\Pi ^{\mathrm {in}}_{2}$
. Using the same reasoning as above, we see that
![]() $\mathbb {Z}^\alpha \cdot \mathbb {Q}$
has Scott sentence complexity
$\mathbb {Z}^\alpha \cdot \mathbb {Q}$
has Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{2\alpha +2}$
. Furthermore, it again follows from results of Ash [Reference Ash5] that
$\Pi ^{\mathrm {in}}_{2\alpha +2}$
. Furthermore, it again follows from results of Ash [Reference Ash5] that
![]() $\omega ^\alpha $
has Scott sentence complexity
$\omega ^\alpha $
has Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{2\alpha +1}$
. These constructions provide examples for all of the claimed cases of the form
$\Pi ^{\mathrm {in}}_{2\alpha +1}$
. These constructions provide examples for all of the claimed cases of the form
![]() $\Pi ^{\mathrm {in}}_{\alpha +n}$
.
$\Pi ^{\mathrm {in}}_{\alpha +n}$
.
This covers every case except for some possibilities that lie close to limit ordinals. The following results fill most of these gaps.
Proposition 4.11. For any limit ordinal
![]() $\lambda ,$
there is a scattered linear ordering of Scott sentence complexity
$\lambda ,$
there is a scattered linear ordering of Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\lambda }.$
$\Pi ^{\mathrm {in}}_{\lambda }.$
Proof. Let
![]() $(\delta _n)_{n\in \omega }$
be a fundamental sequence for
$(\delta _n)_{n\in \omega }$
be a fundamental sequence for
![]() $\lambda $
. We show that
$\lambda $
. We show that
is of the desired complexity.
First note that it indeed does have a
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
Scott sentence. The sentence states the following:
$\Pi ^{\mathrm {in}}_{\lambda }$
Scott sentence. The sentence states the following:
-
(1) There is exactly one 1-block isomorphic to each natural number.
-
(2) These 1-blocks are ordered like the natural numbers.
-
(3) The order between n and
 $n+1$
is isomorphic to
$n+1$
is isomorphic to
 $\mathbb {Z}^{\delta ^n}.$
$\mathbb {Z}^{\delta ^n}.$
This is
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
because each of the items is
$\Pi ^{\mathrm {in}}_{\lambda }$
because each of the items is
![]() $\Pi ^{\mathrm {in}}_{<\lambda }$
. The first two statements can be expressed using finitely many alternations of quantifiers. The final statement can be expressed by the Scott sentence of
$\Pi ^{\mathrm {in}}_{<\lambda }$
. The first two statements can be expressed using finitely many alternations of quantifiers. The final statement can be expressed by the Scott sentence of
![]() $\mathbb {Z}^{\delta _n}$
relativized to the specific interval, this sentence has Scott sentence complexity below
$\mathbb {Z}^{\delta _n}$
relativized to the specific interval, this sentence has Scott sentence complexity below
![]() $\lambda $
by [Reference Alvir and Rossegger3], as the Hausdorff rank of the interval is below
$\lambda $
by [Reference Alvir and Rossegger3], as the Hausdorff rank of the interval is below
![]() $\lambda $
and one can relativize the Scott sentence to the interval using finite quantifier rank by specifying that the elements are between the corresponding finite
$\lambda $
and one can relativize the Scott sentence to the interval using finite quantifier rank by specifying that the elements are between the corresponding finite
![]() $1$
-blocks.
$1$
-blocks.
By Lemma 4.6, the
![]() $\mathbb {Z}^{\delta _n}$
have unbounded Scott rank below
$\mathbb {Z}^{\delta _n}$
have unbounded Scott rank below
![]() $\lambda $
. As these are all
$\lambda $
. As these are all
![]() $\Delta ^{\mathrm {in}}_{0}$
-definable over parameters in
$\Delta ^{\mathrm {in}}_{0}$
-definable over parameters in
![]() $\mathcal {L}_\lambda $
, by [Reference Montalbán20, Lemma 4.3], we have that for each n,
$\mathcal {L}_\lambda $
, by [Reference Montalbán20, Lemma 4.3], we have that for each n,
![]() $SR(\mathcal {L}_\lambda )\geq \delta _n,$
so
$SR(\mathcal {L}_\lambda )\geq \delta _n,$
so
![]() $\Pi ^{\mathrm {in}}_{\lambda }$
is indeed the optimal Scott sentence complexity.
$\Pi ^{\mathrm {in}}_{\lambda }$
is indeed the optimal Scott sentence complexity.
We can use a variation of this construction to get a structure of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{\lambda +2}.$
Unlike some of the previous constructions, this construction is not a sum of shuffle sums, so Corollary 4.3 will not apply.
$\Sigma ^{\mathrm {in}}_{\lambda +2}.$
Unlike some of the previous constructions, this construction is not a sum of shuffle sums, so Corollary 4.3 will not apply.
Theorem 4.12. For any limit ordinal
![]() $\lambda ,$
there is a linear ordering of Scott sentence complexity
$\lambda ,$
there is a linear ordering of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{\lambda +2}.$
$\Sigma ^{\mathrm {in}}_{\lambda +2}.$
Proof. Let
![]() $(\delta _n)_{n\in \omega }$
be a fundamental sequence for
$(\delta _n)_{n\in \omega }$
be a fundamental sequence for
![]() $\lambda $
and let
$\lambda $
and let
Furthermore, define for every n, the linear orderings:
Note that by Lemma 4.6,
![]() $\mathcal {L}_\lambda $
is approximated by the sequence of these orderings in the sense that
$\mathcal {L}_\lambda $
is approximated by the sequence of these orderings in the sense that
![]() $\mathcal {L}_\lambda \equiv _{2\delta _n}\mathcal {L}_{\lambda ,n}.$
$\mathcal {L}_\lambda \equiv _{2\delta _n}\mathcal {L}_{\lambda ,n}.$
Let
![]() $\mathcal {B}=\mathcal {L}_\lambda \cdot (1+\mathbb {Q})$
and
$\mathcal {B}=\mathcal {L}_\lambda \cdot (1+\mathbb {Q})$
and
![]() $\mathcal {A}$
be a copy of
$\mathcal {A}$
be a copy of
![]() $\mathbb {Q}$
where an unbounded, increasing sequence of points
$\mathbb {Q}$
where an unbounded, increasing sequence of points
![]() $c_n$
is replaced by
$c_n$
is replaced by
![]() $\mathcal {L}_{\lambda ,n}$
and each other point is replaced by
$\mathcal {L}_{\lambda ,n}$
and each other point is replaced by
![]() $\mathcal {L}_\lambda $
. We now claim that
$\mathcal {L}_\lambda $
. We now claim that
![]() $\mathcal {K}=\mathcal {A}+\mathcal {B}$
is the desired order. Note that over the parameter of the initial element of
$\mathcal {K}=\mathcal {A}+\mathcal {B}$
is the desired order. Note that over the parameter of the initial element of
![]() $\mathcal {B}$
,
$\mathcal {B}$
,
![]() $pSR(\mathcal {K})=\max (SR(\mathcal {A}),SR(\mathcal {B}))$
(this equality follows from [Reference Gonzalez and Montalbán14, Lemma 11]). We now demonstrate that this quantity is exactly
$pSR(\mathcal {K})=\max (SR(\mathcal {A}),SR(\mathcal {B}))$
(this equality follows from [Reference Gonzalez and Montalbán14, Lemma 11]). We now demonstrate that this quantity is exactly
![]() $\lambda $
.
$\lambda $
.
To define the automorphism orbits of elements within
![]() $\mathcal {B}$
we have to distinguish elements in the initial copy of
$\mathcal {B}$
we have to distinguish elements in the initial copy of
![]() $\mathcal {L}_\lambda $
. For an element
$\mathcal {L}_\lambda $
. For an element
![]() $b\in \mathcal {B}$
, let n be the size of the finite block to the left of b. We can write a formula of finite rank saying that there is precisely one finite block of size n to the left of b and thus use this type of formula to distinguish elements in the first
$b\in \mathcal {B}$
, let n be the size of the finite block to the left of b. We can write a formula of finite rank saying that there is precisely one finite block of size n to the left of b and thus use this type of formula to distinguish elements in the first
![]() $\mathcal {L}_\lambda $
copy. If b is in a finite block we conjunct this formula or its negation with its position in this finite block; if b is in a copy of
$\mathcal {L}_\lambda $
copy. If b is in a finite block we conjunct this formula or its negation with its position in this finite block; if b is in a copy of
![]() $\mathbb {Z}^{\delta _n}$
, then we relativize the formula defining its automorphism orbit in this ordering to the interval restricted by block of size n to the left and a block of size
$\mathbb {Z}^{\delta _n}$
, then we relativize the formula defining its automorphism orbit in this ordering to the interval restricted by block of size n to the left and a block of size
![]() $n+1$
to the right, just as in the proof of Proposition 4.11. Conjuncting this with the formula deciding whether b is in the initial copy of
$n+1$
to the right, just as in the proof of Proposition 4.11. Conjuncting this with the formula deciding whether b is in the initial copy of
![]() $\mathcal {L}_\lambda $
yields the defining formula for its automorphism orbit. To extend this definition to tuples we take the conjunction of the formulas defining orbits for elements and a formula specifying the order of the tuple.
$\mathcal {L}_\lambda $
yields the defining formula for its automorphism orbit. To extend this definition to tuples we take the conjunction of the formulas defining orbits for elements and a formula specifying the order of the tuple.
For
![]() $\mathcal {A}$
the definitions are a little more subtle, but generally follow the same plan. In particular, if the point in
$\mathcal {A}$
the definitions are a little more subtle, but generally follow the same plan. In particular, if the point in
![]() $\mathbb {Q}$
that x lies in between
$\mathbb {Q}$
that x lies in between
![]() $c_n$
and
$c_n$
and
![]() $c_{n+1}$
, then the following describes the automorphism orbit of x:
$c_{n+1}$
, then the following describes the automorphism orbit of x:
-
(1) Let z be the greatest element below x with no successor or predecessor.
-
(2) Let
 $z_n$
be the initial element with no successor or predecessor within
$z_n$
be the initial element with no successor or predecessor within
 $c_n$
; i.e. say that it is the greatest element with no successor or predecessor below an
$c_n$
; i.e. say that it is the greatest element with no successor or predecessor below an
 $n+1$
and
$n+1$
and
 $n+2$
block that bound a structure isomorphic to
$n+2$
block that bound a structure isomorphic to
 $\mathbb {Z}^{\delta _n}$
.
$\mathbb {Z}^{\delta _n}$
. -
(3) Define
 $z_{n+1}$
analogously to
$z_{n+1}$
analogously to
 $z_n$
, expect it is in
$z_n$
, expect it is in
 $c_{n+1}.$
$c_{n+1}.$
-
(4) Say that
 $z_n\leq x<z_{n+1}$
.
$z_n\leq x<z_{n+1}$
. -
(5) Check if
 $z=z_n$
or not.
$z=z_n$
or not. -
(6) In an analogous manner to the case of
 $\mathcal {A}$
, define the automorphism orbit of x within its copy of
$\mathcal {A}$
, define the automorphism orbit of x within its copy of
 $\mathbb {Z}^{\delta _k}$
or the finite block that it is in.
$\mathbb {Z}^{\delta _k}$
or the finite block that it is in.
This describes the automorphism orbit of a point and is of complexity less than
![]() $\Sigma ^{\mathrm {in}}_{\lambda }$
. In order to extend this definition to tuples the only additional detail needed is the order of the tuple and whether the tuples lie in the same point in
$\Sigma ^{\mathrm {in}}_{\lambda }$
. In order to extend this definition to tuples the only additional detail needed is the order of the tuple and whether the tuples lie in the same point in
![]() $\mathbb {Q}$
or not. This can be done by comparing the various values of “z” that emerge for each point in the tuple. To obtain defining formulas for the automorphism orbits of tuples in
$\mathbb {Q}$
or not. This can be done by comparing the various values of “z” that emerge for each point in the tuple. To obtain defining formulas for the automorphism orbits of tuples in
![]() $\mathcal {K}=\mathcal {A}+\mathcal {B}$
, we add the first element of
$\mathcal {K}=\mathcal {A}+\mathcal {B}$
, we add the first element of
![]() $\mathcal {B}$
as a parameter p and restrict the formulas for tuples from
$\mathcal {B}$
as a parameter p and restrict the formulas for tuples from
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {A}$
to elements greater or less than p. As there is no automorphism mapping elements from
$\mathcal {A}$
to elements greater or less than p. As there is no automorphism mapping elements from
![]() $\mathcal {A}$
into elements in
$\mathcal {A}$
into elements in
![]() $\mathcal {B}$
, defining formulas for mixed tuples can be obtained by combining the formulas for tuples in
$\mathcal {B}$
, defining formulas for mixed tuples can be obtained by combining the formulas for tuples in
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
In order to finish the proof, all that remains is to show that
![]() $SR(\mathcal {K})=\lambda +2$
, or in other words, that it has an orbit that is not
$SR(\mathcal {K})=\lambda +2$
, or in other words, that it has an orbit that is not
![]() $\Sigma ^{\mathrm {in}}_{\lambda +1}$
-definable. Let c be the initial point in
$\Sigma ^{\mathrm {in}}_{\lambda +1}$
-definable. Let c be the initial point in
![]() $\mathcal {B}$
and b be some other point in
$\mathcal {B}$
and b be some other point in
![]() $\mathcal {B}$
in a block of size
$\mathcal {B}$
in a block of size
![]() $1$
. We will show that
$1$
. We will show that
![]() $(\mathcal {K},b)\leq _{\lambda +1}(\mathcal {K},c)$
, so the orbit of c is not
$(\mathcal {K},b)\leq _{\lambda +1}(\mathcal {K},c)$
, so the orbit of c is not
![]() $\Sigma ^{\mathrm {in}}_{\lambda +1}$
definable in
$\Sigma ^{\mathrm {in}}_{\lambda +1}$
definable in
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Note that
![]() $\mathcal {K}_{>c}\cong \mathcal {K}_{>b}$
, so it is sufficient to show that
$\mathcal {K}_{>c}\cong \mathcal {K}_{>b}$
, so it is sufficient to show that
![]() $\mathcal {K}_{<b}\leq _{\lambda +1} \mathcal {K}_{<c}.$
As
$\mathcal {K}_{<b}\leq _{\lambda +1} \mathcal {K}_{<c}.$
As
![]() $\mathcal {K}_{<c}$
is an initial segment of
$\mathcal {K}_{<c}$
is an initial segment of
![]() $\mathcal {K}_{<b}$
, for the first turn of the game, the
$\mathcal {K}_{<b}$
, for the first turn of the game, the
![]() $\exists $
-player can pick whatever points the
$\exists $
-player can pick whatever points the
![]() $\forall $
-player picked in
$\forall $
-player picked in
![]() $\mathcal {K}_{<c}$
according to the canonical embedding of
$\mathcal {K}_{<c}$
according to the canonical embedding of
![]() $\mathcal {K}_{<c}$
in
$\mathcal {K}_{<c}$
in
![]() $\mathcal {K}_{<b}$
. Note that each interval is isomorphic except for the one between the greatest chosen points (call them
$\mathcal {K}_{<b}$
. Note that each interval is isomorphic except for the one between the greatest chosen points (call them
![]() $a_k$
) and c or b respectively.
$a_k$
) and c or b respectively.
![]() $a_k$
may be greater than some finite number of the
$a_k$
may be greater than some finite number of the
![]() $c_n$
. Therefore, up to a finite difference in the choice of sequence
$c_n$
. Therefore, up to a finite difference in the choice of sequence
![]() $\delta _n$
used to define
$\delta _n$
used to define
![]() $\mathcal {L}_{\lambda ,n}$
,
$\mathcal {L}_{\lambda ,n}$
,
![]() $(a_k,c)$
is just
$(a_k,c)$
is just
![]() $\mathcal {M}+\mathcal {A}$
where
$\mathcal {M}+\mathcal {A}$
where
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\mathcal {L}_{\lambda ,>c}$
or
$\mathcal {L}_{\lambda ,>c}$
or
![]() $\mathcal {L}_{\lambda ,n,>c}$
depending on which type of order
$\mathcal {L}_{\lambda ,n,>c}$
depending on which type of order
![]() $a_k$
lives in and
$a_k$
lives in and
![]() $(a_k,b)$
is just
$(a_k,b)$
is just
![]() $\mathcal {M}+\mathcal {K}$
. In short, it is enough to demonstrate that
$\mathcal {M}+\mathcal {K}$
. In short, it is enough to demonstrate that
to show the claim. To see this, choose
![]() $\alpha <\lambda $
and show that
$\alpha <\lambda $
and show that
![]() $\mathcal {A}\geq _\alpha \mathcal {K}.$
Take
$\mathcal {A}\geq _\alpha \mathcal {K}.$
Take
![]() $\delta _n>\alpha $
. It is indeed the case that for
$\delta _n>\alpha $
. It is indeed the case that for
![]() $k\geq n$
,
$k\geq n$
,
![]() $\mathcal {L}_{\lambda }\equiv _\alpha \mathcal {L}_{\lambda ,k}$
. For some point d in a block of size
$\mathcal {L}_{\lambda }\equiv _\alpha \mathcal {L}_{\lambda ,k}$
. For some point d in a block of size
![]() $1$
between
$1$
between
![]() $c_n$
and
$c_n$
and
![]() $c_{n+1}$
we have that
$c_{n+1}$
we have that
where
![]() $\mathcal {A}_q\equiv _\alpha \mathcal {L}_{\lambda }\equiv _\alpha \mathcal {B}_q$
. This proves the claim.
$\mathcal {A}_q\equiv _\alpha \mathcal {L}_{\lambda }\equiv _\alpha \mathcal {B}_q$
. This proves the claim.
We need a different construction to deal with the
![]() $\Sigma ^{\mathrm {in}}_{\lambda +3}$
case. However, it is arguably simpler than the construction we used for the example of Scott sentence complexity
$\Sigma ^{\mathrm {in}}_{\lambda +3}$
case. However, it is arguably simpler than the construction we used for the example of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{\lambda +2}$
, as it is a sum of shuffle sums.
$\Sigma ^{\mathrm {in}}_{\lambda +2}$
, as it is a sum of shuffle sums.
Theorem 4.13. For any limit ordinal
![]() $\lambda $
, there is a linear ordering of Scott sentence complexity
$\lambda $
, there is a linear ordering of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{\lambda +3}.$
$\Sigma ^{\mathrm {in}}_{\lambda +3}.$
Proof. We let
![]() $\mathcal {L}_1:=1+\mathbb {Z}+\omega ^\lambda $
and
$\mathcal {L}_1:=1+\mathbb {Z}+\omega ^\lambda $
and
![]() $\mathcal {L}_2:=1+\mathbb {Z}+\omega ^\lambda \cdot 2$
. One important initial observation is that
$\mathcal {L}_2:=1+\mathbb {Z}+\omega ^\lambda \cdot 2$
. One important initial observation is that
![]() $\mathcal {L}_1\leq _{\lambda +1}\mathcal {L}_2$
as
$\mathcal {L}_1\leq _{\lambda +1}\mathcal {L}_2$
as
![]() $\omega ^\lambda \leq _{\lambda +1}\omega ^\lambda \cdot 2$
. As alluded to above, we take
$\omega ^\lambda \leq _{\lambda +1}\omega ^\lambda \cdot 2$
. As alluded to above, we take
![]() $\mathcal {A}=\mathcal {L}_1\cdot \mathbb {Q}$
and
$\mathcal {A}=\mathcal {L}_1\cdot \mathbb {Q}$
and
![]() $\mathcal {B}=\mathcal {L}_2\cdot \mathbb {Q}$
. Finally we let
$\mathcal {B}=\mathcal {L}_2\cdot \mathbb {Q}$
. Finally we let
![]() $\mathcal {L}=\mathcal {A}+\mathcal {L}_2+\mathcal {B}$
and claim that
$\mathcal {L}=\mathcal {A}+\mathcal {L}_2+\mathcal {B}$
and claim that
![]() $\mathcal {L}$
has the desired complexity. Let us begin with showing that
$\mathcal {L}$
has the desired complexity. Let us begin with showing that
![]() $SR(\mathcal {A})\leq \lambda $
. We define several helping predicates from which the claim will easily follow.
$SR(\mathcal {A})\leq \lambda $
. We define several helping predicates from which the claim will easily follow.
-
(1) Let
 $pt(x)$
if x is in a block of size
$pt(x)$
if x is in a block of size
 $1$
.
$1$
. -
(2) Let
 $Z(x)$
say
$Z(x)$
say
 $(\exists z<x) pt(z)\land \forall y~z<y<x \to \bigvee _{n} S^n(y)=x.$
Note that
$(\exists z<x) pt(z)\land \forall y~z<y<x \to \bigvee _{n} S^n(y)=x.$
Note that
 $Z(x)$
holds if and only if x is inside one of the copies of
$Z(x)$
holds if and only if x is inside one of the copies of
 $\mathbb {Z}$
.
$\mathbb {Z}$
. -
(3) Let
 $init(x)$
if
$init(x)$
if
 $(\exists z<x ) pt(z) \land (z,x)\cong \mathbb {Z}.$
Note that
$(\exists z<x ) pt(z) \land (z,x)\cong \mathbb {Z}.$
Note that
 $init(x)$
if and only if x is the first element in a copy of
$init(x)$
if and only if x is the first element in a copy of
 $\omega ^\lambda $
.
$\omega ^\lambda $
. -
(4) For every
 $\gamma <\omega ^\lambda $
let
$\gamma <\omega ^\lambda $
let
 $\gamma (x)$
if
$\gamma (x)$
if
 $(\exists z<x) init(z)\land [z,x)\cong \gamma $
. Note that this definition is of complexity lower than
$(\exists z<x) init(z)\land [z,x)\cong \gamma $
. Note that this definition is of complexity lower than
 $\Sigma ^{\mathrm {in}}_{\lambda }$
as
$\Sigma ^{\mathrm {in}}_{\lambda }$
as
 $\lambda $
is a limit ordinal. It describes the points that are of rank
$\lambda $
is a limit ordinal. It describes the points that are of rank
 $\gamma $
within a copy of
$\gamma $
within a copy of
 $\omega ^{\lambda }$
.
$\omega ^{\lambda }$
.
Using these predicates one can define the automorphism orbits of any tuple in
![]() $\mathcal {L}_1$
, and thus in
$\mathcal {L}_1$
, and thus in
![]() $\mathcal {A}$
, by formulas of complexity less than
$\mathcal {A}$
, by formulas of complexity less than
![]() $\Sigma ^{\mathrm {in}}_{\lambda +1}$
.
$\Sigma ^{\mathrm {in}}_{\lambda +1}$
.
All of these predicates have the same meaning within
![]() $\mathcal {B}$
, however they leave points in the second copy of
$\mathcal {B}$
, however they leave points in the second copy of
![]() $\omega ^\lambda $
undefined. But it is still the case that
$\omega ^\lambda $
undefined. But it is still the case that
![]() $SR(B)\leq \lambda +1$
. To see this we need to define the additional relations:
$SR(B)\leq \lambda +1$
. To see this we need to define the additional relations:
-
(1) Let
This $$\begin{align*}sec(x,z)\iff init(z) \land z<x \land \lnot\exists y\left(z<y<x\land pt(y)\right) \land \bigwedge_{\delta<\lambda}(\forall y<x )y\not\sim_\delta x.\end{align*}$$
$$\begin{align*}sec(x,z)\iff init(z) \land z<x \land \lnot\exists y\left(z<y<x\land pt(y)\right) \land \bigwedge_{\delta<\lambda}(\forall y<x )y\not\sim_\delta x.\end{align*}$$
 $\Pi ^{\mathrm {in}}_{\lambda }$
predicate holds only if z is the initial element in the second copy of
$\Pi ^{\mathrm {in}}_{\lambda }$
predicate holds only if z is the initial element in the second copy of
 $\omega ^{\lambda }$
above the copy that z is initial in.
$\omega ^{\lambda }$
above the copy that z is initial in.
-
(2) For every
 $\gamma <\omega ^\lambda $
let
$\gamma <\omega ^\lambda $
let
 $\gamma _2(x)$
if
$\gamma _2(x)$
if
 $\exists y,z ~ sec(y,z) \land [y,x)\cong \gamma $
. Note that this definition is of complexity
$\exists y,z ~ sec(y,z) \land [y,x)\cong \gamma $
. Note that this definition is of complexity
 $\Sigma ^{\mathrm {in}}_{\lambda +1}$
as
$\Sigma ^{\mathrm {in}}_{\lambda +1}$
as
 $\lambda $
is a limit ordinal. It describes the points that are of rank
$\lambda $
is a limit ordinal. It describes the points that are of rank
 $\gamma $
within a second copy of
$\gamma $
within a second copy of
 $\omega ^{\lambda }$
.
$\omega ^{\lambda }$
.
Using these relations and those defined above, one can define the automorphism orbits of tuples in
![]() $\mathcal {L}_2$
, and thus in
$\mathcal {L}_2$
, and thus in
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
To get defining formulas for tuples in
![]() $\mathcal {A}+\mathcal {L}_2+\mathcal {B}$
one fixes as parameter the first point p in
$\mathcal {A}+\mathcal {L}_2+\mathcal {B}$
one fixes as parameter the first point p in
![]() $\mathcal {L}_2$
, relativizes the defining formulas for tuples in
$\mathcal {L}_2$
, relativizes the defining formulas for tuples in
![]() $\mathcal {A}$
to elements less than p, the defining formulas for tuples in
$\mathcal {A}$
to elements less than p, the defining formulas for tuples in
![]() $\mathcal {L}_2$
to elements such that there is no point between the tuple and p, and the defining formulas for elements of
$\mathcal {L}_2$
to elements such that there is no point between the tuple and p, and the defining formulas for elements of
![]() $\mathcal {B}$
by saying that there is at least one more point between p and the left-most point in the tuple. Using these relativized definitions one can then obtain defining formulas for the automorphism orbits for any tuples in
$\mathcal {B}$
by saying that there is at least one more point between p and the left-most point in the tuple. Using these relativized definitions one can then obtain defining formulas for the automorphism orbits for any tuples in
![]() $\mathcal {A}+\mathcal {L}_2+\mathcal {B}$
.
$\mathcal {A}+\mathcal {L}_2+\mathcal {B}$
.
In order to finish the proof of the claim, we appeal to Corollary 4.3 to show that there is no
![]() $\Pi ^{\mathrm {in}}_{\lambda +3}$
Scott sentence. This follows immediately as
$\Pi ^{\mathrm {in}}_{\lambda +3}$
Scott sentence. This follows immediately as
![]() $\mathcal {A}\leq _{\lambda +1} \mathcal {B}$
is a direct consequence of
$\mathcal {A}\leq _{\lambda +1} \mathcal {B}$
is a direct consequence of
![]() $\mathcal {L}_1\leq _{\lambda +1}\mathcal {L}_2$
.
$\mathcal {L}_1\leq _{\lambda +1}\mathcal {L}_2$
.
This leaves open the case of
![]() $\Sigma ^{\mathrm {in}}_{\lambda +1}$
. It is unclear to us if such a linear ordering exists.
$\Sigma ^{\mathrm {in}}_{\lambda +1}$
. It is unclear to us if such a linear ordering exists.
Question 4.14. Is there a linear ordering of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{\lambda +1}$
for
$\Sigma ^{\mathrm {in}}_{\lambda +1}$
for
![]() $\lambda $
a limit ordinal?
$\lambda $
a limit ordinal?
All of the new examples of Scott sentence complexities given in this section except Proposition 4.11 are linear orderings that contain
![]() $\mathbb {Q}$
as a subordering and are thus non-scattered. While it is not hard to adapt the proof of Theorem 3.6 to obtain that no scattered linear ordering can have Scott sentence complexity
$\mathbb {Q}$
as a subordering and are thus non-scattered. While it is not hard to adapt the proof of Theorem 3.6 to obtain that no scattered linear ordering can have Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{4}$
, it seems difficult to look beyond that. An analysis akin to the one presented in this article, but for Scott sentence complexities of scattered linear orderings seems like it could prove interesting.
$\Sigma ^{\mathrm {in}}_{4}$
, it seems difficult to look beyond that. An analysis akin to the one presented in this article, but for Scott sentence complexities of scattered linear orderings seems like it could prove interesting.
Question 4.15. Which Scott sentence complexities are realized by scattered linear orderings? In particular, for a given successor ordinal
![]() $\alpha>3$
, is there a scattered linear ordering of Scott sentence complexity
$\alpha>3$
, is there a scattered linear ordering of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{\alpha }$
?
$\Sigma ^{\mathrm {in}}_{\alpha }$
?
4.1 Remarks on effectivity
The examples we presented in this section are homogeneous enough so that if
![]() $\alpha $
is a computable ordinal, then the examples witnessing Scott sentence complexity
$\alpha $
is a computable ordinal, then the examples witnessing Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\alpha }$
,
$\Pi ^{\mathrm {in}}_{\alpha }$
,
![]() $\Sigma ^{\mathrm {in}}_{\alpha }$
, or
$\Sigma ^{\mathrm {in}}_{\alpha }$
, or
![]() $d\text{-}\Sigma ^{\mathrm {in}}_{\alpha }$
have computable copies. Furthermore, these structures have c.e. Scott families, that is there is a computable enumeration of codes for the formulas defining the automorphism orbits of the tuples (potentially over a parameter). Thus, our examples give computable linear orderings having computable Scott sentences.
$d\text{-}\Sigma ^{\mathrm {in}}_{\alpha }$
have computable copies. Furthermore, these structures have c.e. Scott families, that is there is a computable enumeration of codes for the formulas defining the automorphism orbits of the tuples (potentially over a parameter). Thus, our examples give computable linear orderings having computable Scott sentences.
The situation is a bit more tricky for examples of high Scott rank, that is computable linear orderings with Scott rank
![]() $\omega _{1}^{\mathrm {CK}}$
or
$\omega _{1}^{\mathrm {CK}}$
or
![]() $\omega _{1}^{\mathrm {CK}}+1$
. Our examples do not give such structures. However, it is not hard to show that such structures exist from existing examples in the literature and our results in Section 2. We note that Calvert, Goncharov, and Knight [Reference Calvert, Goncharov and Knight7] already showed that there are computable linear orderings of Scott rank
$\omega _{1}^{\mathrm {CK}}+1$
. Our examples do not give such structures. However, it is not hard to show that such structures exist from existing examples in the literature and our results in Section 2. We note that Calvert, Goncharov, and Knight [Reference Calvert, Goncharov and Knight7] already showed that there are computable linear orderings of Scott rank
![]() $\omega _{1}^{\mathrm {CK}}$
and
$\omega _{1}^{\mathrm {CK}}$
and
![]() $\omega _{1}^{\mathrm {CK}}+1$
. The following result is merely a refinement.
$\omega _{1}^{\mathrm {CK}}+1$
. The following result is merely a refinement.
Theorem 4.16. There are computable linear orderings with Scott sentence complexities
![]() $\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}}$
,
$\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}}$
,
![]() $\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
, and
$\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
, and
![]() $\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+2}$
.
$\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+2}$
.
Proof. As is remarked in [Reference Alvir, Greenberg, Harrison-Trainor and Turetsky1], the Harrison linear ordering
![]() $\omega _{1}^{\mathrm {CK}}\cdot (1+\mathbb {Q})$
has Scott sentence complexity
$\omega _{1}^{\mathrm {CK}}\cdot (1+\mathbb {Q})$
has Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+2}$
. The existence of structures of linear orderings of Scott sentence complexity
$\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+2}$
. The existence of structures of linear orderings of Scott sentence complexity
![]() $\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
and
$\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
and
![]() $\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}}$
follows from Theorem 2.19 and the existence of a computable graph with these Scott sentence complexities.
$\Pi ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}}$
follows from Theorem 2.19 and the existence of a computable graph with these Scott sentence complexities.
As for general limit ordinals we do not know whether there are computable linear orderings of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
. Additionally, we do not know whether there is a computable linear of Scott rank
$\Sigma ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
. Additionally, we do not know whether there is a computable linear of Scott rank
![]() $d\text{-}\Sigma ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
.
$d\text{-}\Sigma ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
.
Question 4.17. Is there a computable linear ordering of Scott sentence complexity
![]() $\Sigma ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
?
$\Sigma ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
?
Question 4.18. Is there a computable linear ordering of Scott sentence complexity
![]() $d\text{-}\Sigma ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
?
$d\text{-}\Sigma ^{\mathrm {in}}_{\omega _{1}^{\mathrm {CK}}+1}$
?
Funding
The work of Rossegger was supported by the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement no. 101026834 – ACOSE.