In a recent work on 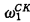-recursivity ([M] in which the principal result of [G.2] is obtained by more direct methods) I have given a very simple lemma on the structure of the so-called rungs [G.1] which enables us to describe precisely the relation they have with Jervell's tree [J] in the wellfounded case (R.O. Gandy has also worked out this relation in the wellfounded case, but with techniques very different from those introduced here).

In the present work I treat the general case in §§I and II. The results are summarized in §III. These results are then exploited by means of the operator Σ*, which is the principal tool of Lemma (4.1) (i.e. the generalized version of the previous structural lemma). A systematical use of Σ* is also the basis of the study of ladders in the last section.

Recall that the notions of rungs and ladders were introduced by J.-Y. Girard [G, 0] and [G.1] as a basic tool for ordinal analysis of Π½-logic (i.e. roughly speaking, logic with β-rule) and the introduction of trees and homogeneous trees by H.R. Jervell is a first attempt to give to these notions a geometrical interpretation without any explicit mention of functors and categorical limits. In fact, as it is evident in the last section of the present paper, limits play a modest role in the study of ladders, but their properties with respect to limits are of fundamental interest in their applications (a domain which is out of the scope of this basic work. Readers interested in applications to ordinal analysis are invited to consult the references). Note that my trees are not exactly those introduced by H.R. Jervell: his extra symbols λ and ρ are respectively changed into 0 and the type of the concerned tree. More important is the fact that we consider only the extremal nodes of the trees. The objects so obtained are then as close as possible to Girard's dendroids.

I am indebted to J.-Y. Girard for his advice about my work.