Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Wei
2014.
Cohesive sets and rainbows.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 2,
p.
389.
Wang, Wei
2014.
Some logically weak Ramseyan theorems.
Advances in Mathematics,
Vol. 261,
Issue. ,
p.
1.
Kang, Xiaojun
2014.
Combinatorial principles between RRT 2 2 and RT 2 2.
Frontiers of Mathematics in China,
Vol. 9,
Issue. 6,
p.
1309.
Liu, Lu
2014.
Cone avoiding closed sets.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 3,
p.
1609.
Patey, Ludovic
2015.
Ramsey-type graph coloring and diagonal non-computability.
Archive for Mathematical Logic,
Vol. 54,
Issue. 7-8,
p.
899.
Flood, Stephen
2015.
A packed Ramsey’s theorem and computability theory.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 7,
p.
4957.
Rice, Brian
2015.
The Thin Set Theorem for Pairs Implies DNR.
Notre Dame Journal of Formal Logic,
Vol. 56,
Issue. 4,
Flood, Stephen
and
Towsner, Henry
2016.
Separating principles below.
Mathematical Logic Quarterly,
Vol. 62,
Issue. 6,
p.
507.
Hirschfeldt, Denis R.
and
Jockusch, Carl G.
2016.
On notions of computability-theoretic reduction between Π21 principles.
Journal of Mathematical Logic,
Vol. 16,
Issue. 01,
p.
1650002.
Steila, Silvia
and
Yokoyama, Keita
2016.
Reverse mathematical bounds for the Termination Theorem.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 12,
p.
1213.
Patey, Ludovic
2016.
The weakness of being cohesive, thin or free in reverse mathematics.
Israel Journal of Mathematics,
Vol. 216,
Issue. 2,
p.
905.
PATEY, LUDOVIC
2016.
OPEN QUESTIONS ABOUT RAMSEY-TYPE STATEMENTS IN REVERSE MATHEMATICS.
The Bulletin of Symbolic Logic,
Vol. 22,
Issue. 2,
p.
151.
Bienvenu, Laurent
Patey, Ludovic
and
Shafer, Paul
2017.
On the logical strengths of partial solutions to mathematical problems.
Transactions of the London Mathematical Society,
Vol. 4,
Issue. 1,
p.
30.
Skrzypczak, Michał
2017.
Developments in Language Theory.
Vol. 10396,
Issue. ,
p.
75.
Eastaugh, Benedict
2017.
Book Reviews.
Studia Logica,
Vol. 105,
Issue. 4,
p.
873.
Hirschfeldt, Denis R.
2017.
Computability and Complexity.
Vol. 10010,
Issue. ,
p.
22.
Dzhafarov, Damir D.
and
Patey, Ludovic
2017.
Coloring trees in reverse mathematics.
Advances in Mathematics,
Vol. 318,
Issue. ,
p.
497.
Patey, Ludovic
and
Yokoyama, Keita
2018.
The proof-theoretic strength of Ramsey's theorem for pairs and two colors.
Advances in Mathematics,
Vol. 330,
Issue. ,
p.
1034.
Csima, Barbara F.
Dzhafarov, Damir D.
Hirschfeldt, Denis R.
Jockusch, Jr., Carl G.
Solomon, Reed
Brown Westrick, Linda
Brattka, Vasco
Downey, Rod
Knight, Julia F.
and
Lempp, Steffen
2019.
The reverse mathematics of Hindman’s Theorem for sums of exactly two elements.
Computability,
Vol. 8,
Issue. 3-4,
p.
253.
Monin, Benoit
and
Patey, Ludovic
2019.
Pigeons do not jump high.
Advances in Mathematics,
Vol. 352,
Issue. ,
p.
1066.


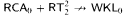 by showing that for any set
by showing that for any set 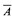 such that
such that 