Let X be an infinite but separable metric space. An open cover 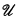of X is said to be large if for each x ϵ X the set {U ϵ 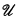: x ϵ U} is infinite. The symbol Λ denotes the collection of large open covers of X. An open cover 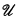of X is said to be an ω-cover if for each finite subset F of X there is a U ϵ 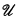such that F ⊆ U, and X is not a member of 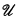, X is said to have Rothberger's property if there is for every sequence (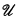n : n = 1,2,3,…) of open covers of X a sequence (Un : n = 1,2,3,…) such that:

(1) for each n, Un is a member of 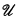n, and

(2) {Un: n = 1,2,3,…} is a cover of X.

Rothberger introduced this property in his paper [2]. For convenience we let 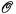denote the collection of all open covers of X.

In [3] it was shown that X has Rothberger's property if, and only if, the following partition relation is true for large open covers of X:

This partition relation means:

for every large cover 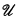of X, for every coloring

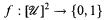
such that for each U ϵ 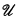and each large cover 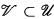there is an i with 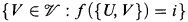a large cover of X,

either there is a large cover 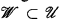such that f({A, B}) = 0 whenever {A,B} ϵ ,

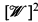or else there is a 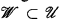which is not point–finite such that f{{A, B}) = 1 whenever {A, B} ϵ .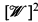