Article contents
Recursive Boolean algebras with recursive atoms
Published online by Cambridge University Press: 12 March 2014
Extract
A Boolean algebra (henceforth abbreviated B.A.) 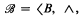
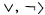 is said to be recursive if B is a recursive subset of the natural numbers N and the operations ∧ (meet), ∨ (join), and ¬ (complement) are partial recursive. Let
is said to be recursive if B is a recursive subset of the natural numbers N and the operations ∧ (meet), ∨ (join), and ¬ (complement) are partial recursive. Let 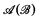 denote the set of atoms of
denote the set of atoms of 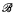 and
and 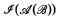 denote the ideal generated by the atoms of
denote the ideal generated by the atoms of 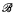 . Given recursive B.A.s
. Given recursive B.A.s 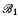 and
and 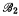 , we write
, we write 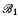 ≈
≈ 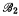 if
if 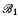 is isomorphic to
is isomorphic to 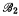 and
and 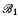 ≈r
≈r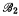 if
if 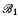 is recursively isomorphic to
is recursively isomorphic to 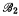 , i.e., if there is a partial recursive isomorphism from
, i.e., if there is a partial recursive isomorphism from 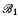 onto
onto 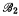 .
.
Recursive B.A.s have been studied by several authors including Ershov [2], Fiener [3], [4], Goncharov [5], [6], [7], LaRoche [8], Nurtazin [7], and the author [10], [11]. This paper continues a study of the recursion theoretic relationships among 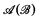 ,
, 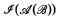 , and the recursive isomorphism type of a recursive B.A.
, and the recursive isomorphism type of a recursive B.A. 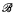 we started in [11]. We refer the reader to [11] for any unexplained notation and definitions. In [11], we were mainly concerned with the possible recursion theoretic properties of the set of atoms in recursive B.A.s. We found that even if we insist that
we started in [11]. We refer the reader to [11] for any unexplained notation and definitions. In [11], we were mainly concerned with the possible recursion theoretic properties of the set of atoms in recursive B.A.s. We found that even if we insist that 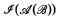 be recursive, there is considerable freedom for the properties of
be recursive, there is considerable freedom for the properties of 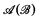 . For example, we showed that if
. For example, we showed that if 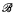 is a recursive B.A. such that
is a recursive B.A. such that 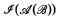 is recursive and
is recursive and 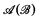 is infinite, then (i) there exists a recursive B.A.
is infinite, then (i) there exists a recursive B.A. 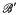 such that
such that 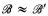 and both
and both 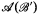 and
and 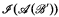 are recursive and (ii) for any nonzero r.e. degree δ, there exist recursive B.A.s
are recursive and (ii) for any nonzero r.e. degree δ, there exist recursive B.A.s 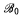 ,
, 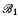 , … such that for each i,
, … such that for each i, 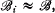
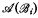 is of degree δ,
is of degree δ, 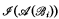 is recursive,
is recursive, 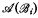 is immune if i is even and
is immune if i is even and 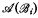 is not immune if i is odd, and no two B.A.s in the sequence are recursively isomorphic.
is not immune if i is odd, and no two B.A.s in the sequence are recursively isomorphic.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
References
REFERENCES
- 21
- Cited by


