Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T07:14:27.636Z Has data issue: false hasContentIssue false
  • English
  • Français

A proof theoretic proof of Scott's general interpolation theorem

Published online by Cambridge University Press:  12 March 2014

Henry Africk
Henry Africk*
Affiliation:
University of Missouri, St Louis, Missouri 63121
Get access Rights & Permissions [Opens in a new window]

Extract

In [5] Scott asked if there was a proof theoretic proof of his interpolation theorem. The purpose of this paper is to provide such a proof, working with the first order system LK of Gentzen [2]. Our method is an extension of the one in Maehara [3] for Craig's interpolation theorem. We will also sketch the original model theoretic proof and show how Scott used his result to obtain a definability theorem of Svenonius [7].

A language for LK contains the usual logical symbols: 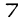, ∧, ∨, ⊃, ∀, ∃; countably many free variables a0, a1, … and bound variables x0, x1, …; and some or all of the following nonlogical symbols: n-ary predicates 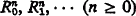; n-ary functions 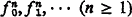; and individual constants c0, c1, …. Semiterms are defined as follows: (1) Free variables, bound variables and individual constants are semiterms. (2) If f is an n-ary function and s1 …, sn are semiterms, then f(s1 …, sn), is a semiterm. A term is a semiterm that does not contain a bound variable. Formulas are defined as follows: (1) If R is an n-ary predicate and t1 …, tn are terms, then R(t1 …, tn) is a formula. (2) If A and B are formulas, then 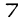A, A ∧ B, A ∨ B and A ⊃ B are formulas. (3) If A(t) is a formula which has zero or more occurrences of the term t, and if x is a bound variable not contained in A(t), then ∀xA(x) and ∃xA(x) are formulas where A(x) is obtained from A(t) by substituting x for t at all indicated places.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 4 , December 1972 , pp. 683 - 695
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Craig, W., Three uses of the Herbrand-Gentzen theorem in relating model theory and proof theory, this Journal, vol. 22 (1957), pp. 269–285.Google Scholar
[2]Gentzen, G., Untersuchungen über das logische Schliessen, Mathematische Zeitschrift, vol. 39 (1934/1935), pp. 176–210, 405–431.CrossRefGoogle Scholar
[3]Maehara, S., Craig's interpolation theorem, Sûgaku, vol. 12 (1961), pp. 235–237 (Japanese)Google Scholar
[4]Robinson, A., Introduction to model theory and to the metamathematics of algebra, North-Holland, Amsterdam, 1965.Google Scholar
[5]Scott, D., Interpolation theorems, Third International Congress for Logic, Methodology and Philosophy of Science, Amsterdam, 1967 (unpublished).Google Scholar
[6]Specker, E., Typical ambiguity, Logic, methodology and philosophy of science, Stanford University Press, Stanford, 1962, pp. 116–124.Google Scholar
[7]Svenonius, L., A theorem on permutations in models, Theoria, vols. 24 and 25 (1958–1959), pp. 173–178.Google Scholar