Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T04:21:25.527Z Has data issue: false hasContentIssue false
  • English
  • Français

Power-like models of set theory

Published online by Cambridge University Press:  12 March 2014

Ali Enayat
Ali Enayat*
Affiliation:
Department of Mathematics and Statistics, American University, Washington, D.C. 20016-8050, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

A model 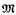= (M. E, …) of Zermelo-Fraenkel set theory ZF is said to be 0-like. where E interprets ∈ and θ is an uncountable cardinal, if ∣M∣ = θ but ∣{b ∈ M: bEa}∣ < 0 for each a ∈ M, An immediate corollary of the classical theorem of Keisler and Morley on elementary end extensions of models of set theory is that every consistent extension of ZF has an ℵ1-like model. Coupled with Chang's two cardinal theorem this implies that if θ is a regular cardinal 0 such that 2<0 = 0 then every consistent extension of ZF also has a 0+-like model. In particular, in the presence of the continuum hypothesis every consistent extension of ZF has an ℵ2-like model. Here we prove:

Theorem A. If 0 has the tree property then the following are equivalent for any completion T of ZFC:

(i) T has a 0-like model.

(ii) Ф ⊆ T. where Ф is the recursive set of axioms {∃κ (κ is n-Mahlo and “Vκis a Σn-elementary submodel of the universe”): n ∈ ω}.

(iii) T has a λ-like model for every uncountable cardinal λ.

Theorem B. The following are equiconsistent over ZFC:

(i) “There exists an ω-Mahlo cardinal”.

(ii) “For every finite language 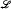, all ℵ2-like models of ZFC(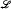) satisfy the schemeФ().

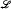Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 4 , December 2001 , pp. 1766 - 1782
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[A]Abraham, U., Aronszajn trees on ℵ2 and ℵ3, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 213–230.CrossRefGoogle Scholar
[B]Boos, W., Boolean extensions which efface the Mahlo property, this Journal, vol. 39 (1974), pp. 254–268.Google Scholar
[C]Chang, C. C., A note on the two cardinal problem, Proceedings of the American Mathematical Society, vol. 16 (1965), pp. 1148–1152.CrossRefGoogle Scholar
[CK]Chang, C. C. and Keisler, H. J., Model theory, North Holland, 1973.Google Scholar
[CF]Cummings, J. and Foreman, M., The tree property, Advances in Mathematics, vol. 133 (1998), pp. 1 32.CrossRefGoogle Scholar
[D]Devlin, K., Constructihility, Springer-Verlag, Berlin-Heidelberg, 1984.CrossRefGoogle Scholar
[E-I]Enayat, A., On certain elementary extensions of models of set theory, Transactions of the American Mathematical Society, vol. 283 (1984), pp. 705–715.CrossRefGoogle Scholar
[E-2]Enayat, A., Conservative elementary extensions of models of set theory and generalizations, this Journal, vol. 51 (1986), pp. 1005–1021.Google Scholar
[E-3]Enayat, A., Analogues of the MacDowell-Specker theorem for set theory, Models, algebras, and proofs, Lecture Notes in Pure and Applied Mathematics, vol. 203, Marcel Decker Inc., New York-Basel, 1999.Google Scholar
[ER]Erdös, P. and Rado, R., A partition calculus in set theory, Bulletin of the American Mathematical Society, vol. 62 (1956), pp. 427–489.CrossRefGoogle Scholar
[Fe]Felgner, U., Comparisons of the axioms of local and universal choice, Fundamenta Mathematicae, vol. 56 (1971), pp. 43–62.CrossRefGoogle Scholar
[Fu]Fuhrken, G., Languages with the added quantifier “there exists at least ℵα”, The theory of models (Addison, J. W., Henkin, L., and Tarski, A., editors), North Holland, Amsterdam, 1961, pp. 121–131.Google Scholar
[Kan]Kanamori, A., The higher infinite, Springer-Verlag, New York, 1994.Google Scholar
[Kau-1]Kaufmann, M., The existence of Σn end extensions, Logic year 1979–80, University of Connecticut (Lerman, et al., editor), Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 92–103.CrossRefGoogle Scholar
[Kau-2]Kaufmann, M., Blunt and topless extensions of models of set theory, this Journal, vol. 48 (1983), pp. 1053–1073.Google Scholar
[Ke-1]Keisler, H. J., Models with orderings, pp. 35–62, North-Holland, Amsterdam, 1967, pp. 35–62.Google Scholar
[Ke-2]Keisler, H. J., Models with tree structures, Proceedings of symposia in pure mathematics, (Tarski symposium), vol. 25, American Mathematical Society, Providence, RI, 1974, pp. 35–62.Google Scholar
[KM]Keisler, H. J. and Morley, M., Elementary extensions of models of set theory, Israel Journal of Mathematics, vol. 6 (1986), pp. 49–65.CrossRefGoogle Scholar
[KS]Keisler, H. J. and Silver, J., End extensions of models of set theory, Proceedings of symposia in pure mathematics (Providence, RI), vol. 13, American Mathematical Society, 1970, pp. 177–187.Google Scholar
[Ku-1]Kunen, K., Some applications of iterated ultrapowers in set theory, Annals of Mathematical Logic, (1970), pp. 179–227.CrossRefGoogle Scholar
[Ku-2]Kunen, K., Set theory, North-Holland, Amsterdam, 1980.Google Scholar
[L]Lévy, A., A hierarchy of formulas in set theory, Memoirs of the American Mathematical Society (Providence, RI), no. 57, 1965.Google Scholar
[Mac-Sp]MacDowell, R. and Specker, E., Modelle der Arithmetik, Infinitistic methods, Pergamon, Oxford, 1961, pp. 257–263.Google Scholar
[MS]Magidor, M. and Shelah, S., The tree property at successors of singular cardinals, Archive for Mathematical Logic, vol. 35 (1996), pp. 385–404.CrossRefGoogle Scholar
[M]Mitchell, W., Aronszajn trees and the independence of the transfer property, Annals of Mathematical Logic, (1972), pp. 21–46.Google Scholar
[Sch-1]Schmerl, J., Generalizing special Aronszajn trees, this Journal, vol. 39 (1974), pp. 732–740.Google Scholar
[Sch-2]Schmerl, J., Transfer theorems and their applications to logics, Model theoretic logics (Barwise, J. and Fefferman, S., editors), Springer-Verlag, New York, 1985, pp. 177–209.Google Scholar
[SS]Schmerl, J. and Shelah, S., On power-like models for hyperinacessihle cardinals, this Journal, vol. 37 (1972), pp. 531–537.Google Scholar
[Sh]Shelah, S., Models with second order properties II: trees with no undefined branches, Annals of Mathematical Logic, vol. 14 (1978), pp. 73–87.CrossRefGoogle Scholar