Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hajnal, András
and
Larson, Jean A.
2010.
Handbook of Set Theory.
p.
129.
Larson, Jean A.
2012.
Sets and Extensions in the Twentieth Century.
Vol. 6,
Issue. ,
p.
145.
Larson, J. A.
2017.
In memoriam: James Earl Baumgartner (1943–2011).
Archive for Mathematical Logic,
Vol. 56,
Issue. 7-8,
p.
877.
Garti, Shimon
2019.
Bipartite Graphs and Monochromatic Squares.
Order,
Vol. 36,
Issue. 1,
p.
99.


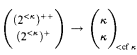 , and if
, and if 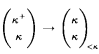 .
.