Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-22T13:12:35.542Z Has data issue: false hasContentIssue false
  • English
  • Français

Partitioning subsets of stable models

Published online by Cambridge University Press:  12 March 2014

Timothy Bays
Timothy Bays*
Affiliation:
University of Notre Dame, Department of Philosophy, Notre Dame, IN 46556, USA, E-Mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

This paper discusses two combinatorial problems in stability theory. First we prove a partition result for subsets of stable models: for any A and B, we can partition A into ∣B∣<κ(T) pieces. 〈Ai ∣ i < ∣B∣<κ(T)〉. such that for each Ai there is a Bi ⊆ B where ∣Bi∣ < κ(T) and 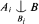, Second, if A and B are as above and ∣A∣ > ∣B∣, then we try to find A′ ⊂ A and B′ ⊂ B such that ∣A′∣ is as large as possible. ∣B′∣ is as small as possible, and 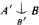. We prove some positive results in this direction, and we discuss the optimality of these results under ZFC + GCH.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 4 , December 2001 , pp. 1899 - 1908
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, J., Fundamentals of Stability Theory, Springer-Verlag, Berlin, 1988.CrossRefGoogle Scholar
[2]Bays, T., Multi-cardinal phenomena in stable theories, Ph.D. thesis, University of California, Los Angeles, 1994.Google Scholar
[3]Levinski, J. P., Magidor, M., and Shelah, S., Chang's Conjecture for ℵω, Israel Journal of Mathematics, vol. 69 (1990), pp. 161–172.CrossRefGoogle Scholar
[4]Pillay, A., An Introduction to Stability Theory, Clarendon Press, Oxford, 1983.Google Scholar
[5]Shelah, S., Classification theory and the number of non-isomorphic models, North-Holland, Amsterdam, 1990.Google Scholar