Article contents
On supervaluations in free logic
Published online by Cambridge University Press: 12 March 2014
Extract
The concepts “classical valuation” and “supervaluation” were introduced by van Fraassen around 1966, to provide a semantic analysis of the then extant axiomatic systems of free logic. Consider an atomic sentence

and a “partial” model 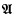 which fails to interpret c. Then (1) has no truth value in
which fails to interpret c. Then (1) has no truth value in 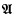 , nor does
, nor does

While the valuelessness of (1) was found intuitively acceptable, that of (2) was not. Indeed, (2) and all other tautologies are theorems of free logic.
Van Fraassen found a way to accommodate both intuitions. He interprets the unproblematic atomic sentences as usual, while “interpreting” those like (1) by simply assigning them a truth-value in arbitrary fashion. Then a truth-value for every sentence can be defined in the usual way; the result van Fraassen calls a “classical valuation” of the language. The arbitrary element in any given classical valuation is then eliminated by passage to the “supervaluation” over 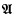 , which agrees with the classical valuations where they agree among themselves, and otherwise is undefined. In the supervaluation over
, which agrees with the classical valuations where they agree among themselves, and otherwise is undefined. In the supervaluation over 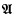 , (1) is valueless but (2) true (since true on all classical valuations), as was required.
, (1) is valueless but (2) true (since true on all classical valuations), as was required.
There is a slight, but crucial oversimplification in the preceding account. Evaluation of the sentence

requires prior evaluation of the open formula

But here mere assignment of truth-value is not enough; a whole set must be arbitrarily assigned as extension. The quantification over classical valuations involved in passage to the supervaluation thus involves an implicit quantification over subsets of the domain of 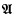 : supervaluations are second order.
: supervaluations are second order.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 14
- Cited by


