1 Introduction
In the book ‘The Core Model Iterability Problem’ [Reference Steel10, p. 28], John Steel conjectured the following:
Conjecture 1. Let
![]() $\mathcal {W}$
and
$\mathcal {W}$
and
![]() $\mathcal {R}$
be
$\mathcal {R}$
be
![]() $1$
-small weasels which are
$1$
-small weasels which are
![]() $\Omega +1$
-iterable. Then the following are equivalent
$\Omega +1$
-iterable. Then the following are equivalent
![]() $:$
$:$
-
1.
 $\mathcal {W}\leq ^{*}\mathcal {R}$
, and
$\mathcal {W}\leq ^{*}\mathcal {R}$
, and -
2. there is a club
 $C \subset \Omega $
such that
$C \subset \Omega $
such that
 $(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
for all regular cardinals
$(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
for all regular cardinals
 $\alpha \in C$
.
$\alpha \in C$
.
In the terminology of the book a weasel is premouse of ordinal height
![]() $\Omega $
, where
$\Omega $
, where
![]() $\Omega $
is a fixed measurable cardinal. The relation
$\Omega $
is a fixed measurable cardinal. The relation
![]() $\leq ^{*}$
is the mouse order, i.e., if
$\leq ^{*}$
is the mouse order, i.e., if
![]() $\mathcal {W}$
and
$\mathcal {W}$
and
![]() $\mathcal {R}$
are weasels which are sufficiently iterable to successfully coiterate (by results of the book
$\mathcal {R}$
are weasels which are sufficiently iterable to successfully coiterate (by results of the book
![]() $\Omega +1$
-iterability suffices), then
$\Omega +1$
-iterability suffices), then
![]() $\mathcal {W}\leq ^{*}\mathcal {R}$
if and only if
$\mathcal {W}\leq ^{*}\mathcal {R}$
if and only if
![]() $\mathcal {R}$
wins the coiteration, i.e. if
$\mathcal {R}$
wins the coiteration, i.e. if
![]() $(\mathcal {T},\mathcal {U})$
is the successful coiteration of
$(\mathcal {T},\mathcal {U})$
is the successful coiteration of
![]() $(\mathcal {W},\mathcal {R})$
and
$(\mathcal {W},\mathcal {R})$
and
![]() $\operatorname {\mathrm {lh}}(T)=\theta +1$
and
$\operatorname {\mathrm {lh}}(T)=\theta +1$
and
![]() $\operatorname {\mathrm {lh}}(\mathcal {U})=\gamma +1$
, then
$\operatorname {\mathrm {lh}}(\mathcal {U})=\gamma +1$
, then
![]() $\mathcal {M}_{\theta }^{\mathcal {T}}\unlhd \mathcal {M}_{\gamma }^{\mathcal {U}}$
.
$\mathcal {M}_{\theta }^{\mathcal {T}}\unlhd \mathcal {M}_{\gamma }^{\mathcal {U}}$
.
Steel showed in [Reference Steel10] that Conjecture 1 holds for weasels small enough that linear iterations suffice for comparison. His proof is based on universal linear iterations.
In the following we will prove Conjecture 1 under the assumption that neither
![]() $\mathcal {W}$
nor
$\mathcal {W}$
nor
![]() $\mathcal {R}$
have an initial segment which models the theory KP + “there is a Woodin cardinal”, see Theorem 26. In particular, Conjecture 1 holds if there is no transitive model of KP + “there is a Woodin cardinal”.
$\mathcal {R}$
have an initial segment which models the theory KP + “there is a Woodin cardinal”, see Theorem 26. In particular, Conjecture 1 holds if there is no transitive model of KP + “there is a Woodin cardinal”.
On the other hand, assuming the existence of an iterable admissible passive premouse M with a ![]() -Woodin cardinal,Footnote
1
we will show that there is an inner model that thinks there is a counterexample to Conjecture 1, see Section 4.2.
-Woodin cardinal,Footnote
1
we will show that there is an inner model that thinks there is a counterexample to Conjecture 1, see Section 4.2.
For the construction of the counterexample from the assumption just described we will need to investigate the extender algebra over admissible mice. In the course of this, we will show that if M is an iterable premouse modelling KP with a largest, regular, uncountable cardinal
![]() $\delta $
,
$\delta $
,
![]() $\mathbb {P} \in M$
is a forcing poset such that
$\mathbb {P} \in M$
is a forcing poset such that
![]() $M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}"$
, and
$M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}"$
, and
![]() $g \subseteq \mathbb {P}$
is M-generic,
$g \subseteq \mathbb {P}$
is M-generic,
![]() $M[g] \models \text {KP}$
, see Theorem 10.
$M[g] \models \text {KP}$
, see Theorem 10.
In Section 5 we will answer another question implicit in remarks from [Reference Steel10, p. 32] about the S-hull property in
![]() $1$
-small weasels. We will show that for any
$1$
-small weasels. We will show that for any
![]() $\Omega +1$
-iterable weasel
$\Omega +1$
-iterable weasel
![]() $\mathcal {W}$
such that
$\mathcal {W}$
such that
![]() $\Omega $
is S-thick in
$\Omega $
is S-thick in
![]() $\mathcal {W}$
the set of points that have the S-hull property is almost closed, see Theorem 37 and Definition 36.
$\mathcal {W}$
the set of points that have the S-hull property is almost closed, see Theorem 37 and Definition 36.
We will use the notation from [Reference Schlutzenberg9]. A k-maximal iteration tree is as in Definition 3.4 of [Reference Steel11].
2 Admissible premice
Definition 2. A passiveFootnote
2
premouse
![]() $M=(\lfloor M \rfloor ,\in ,\mathbb {E}^{M},\emptyset )$
is called admissible if
$M=(\lfloor M \rfloor ,\in ,\mathbb {E}^{M},\emptyset )$
is called admissible if
![]() $M\models \text {KP}$
.Footnote
3
$M\models \text {KP}$
.Footnote
3
Remark. Note that an active premouse M, i.e. so that
![]() $F^M \neq \emptyset $
, cannot model KP. We leave this as an exercise.
$F^M \neq \emptyset $
, cannot model KP. We leave this as an exercise.
For
![]() $n\leq \omega $
, we say an n-sound premouse M is n-countably iterable if every countable elementary substructure of M is
$n\leq \omega $
, we say an n-sound premouse M is n-countably iterable if every countable elementary substructure of M is
![]() $(n,\omega _{1},\omega _{1}+1)^{*}$
-iterable. If M is
$(n,\omega _{1},\omega _{1}+1)^{*}$
-iterable. If M is
![]() $\omega $
-countably iterable we also say that M is countably iterable.
$\omega $
-countably iterable we also say that M is countably iterable.
The following is a nice criterion for the admissibility of a passive premouse, whose proof we leave to the reader.
Lemma 3. Let M be a passive premouse. Then
![]() $M\models \text {KP}$
if and only if for all
$M\models \text {KP}$
if and only if for all
![]() $f\in \Sigma _{1}^{M}(M)$
such that f is a function with
$f\in \Sigma _{1}^{M}(M)$
such that f is a function with
![]() $\operatorname {\mathrm {dom}}(f)\in M$
,
$\operatorname {\mathrm {dom}}(f)\in M$
,
![]() $f\in M$
.
$f\in M$
.
Moreover, if M has a largest cardinal
![]() $\delta $
, then
$\delta $
, then
![]() $M\models \text {KP}$
if and only if for all
$M\models \text {KP}$
if and only if for all
![]() ${f\in \Sigma _{1}^{M}(M)}$
such that f is a function with
${f\in \Sigma _{1}^{M}(M)}$
such that f is a function with
![]() $\operatorname {\mathrm {dom}}(f)=\delta $
,
$\operatorname {\mathrm {dom}}(f)=\delta $
,
![]() $f\in M$
.
$f\in M$
.
Remark. If M is a
![]() $0$
-countably iterable premouse without a largest cardinal, then M is admissible. The proof of this uses the Condensation Lemma.
$0$
-countably iterable premouse without a largest cardinal, then M is admissible. The proof of this uses the Condensation Lemma.
Lemma 4. Suppose M is an admissible passive premouse. If
![]() $\rho _{1}^{M}<\operatorname {\mathrm {OR}}^{M}$
, then
$\rho _{1}^{M}<\operatorname {\mathrm {OR}}^{M}$
, then
![]() $\rho _{1}^{M}$
is the largest cardinal of M.
$\rho _{1}^{M}$
is the largest cardinal of M.
Proof. Let
![]() $\rho :=\rho _{1}^{M}$
. Assume for the sake of contradiction that
$\rho :=\rho _{1}^{M}$
. Assume for the sake of contradiction that
![]() $\rho ^{+M}$
exists, i.e.,
$\rho ^{+M}$
exists, i.e.,
![]() $\rho ^{+M}<\operatorname {\mathrm {OR}}^{M}$
. Let
$\rho ^{+M}<\operatorname {\mathrm {OR}}^{M}$
. Let
Let
![]() $\xi :=\sup (H^{\prime }\cap \rho ^{+M})$
. Suppose first that
$\xi :=\sup (H^{\prime }\cap \rho ^{+M})$
. Suppose first that
![]() $\xi =\rho ^{+M}$
. In this case by the upwards absoluteness of
$\xi =\rho ^{+M}$
. In this case by the upwards absoluteness of
![]() $\Sigma _{1}$
formulas
$\Sigma _{1}$
formulas
Note that the part of the formula in parentheses is
![]() $\Sigma _{1}$
. Thus, by
$\Sigma _{1}$
. Thus, by
![]() $\Delta _{0}$
-collection, there is some
$\Delta _{0}$
-collection, there is some
![]() $\gamma <\operatorname {\mathrm {OR}}^{M}$
such that
$\gamma <\operatorname {\mathrm {OR}}^{M}$
such that
Thus, there is
![]() $f\in J(M\vert \gamma )\unlhd M$
such that
$f\in J(M\vert \gamma )\unlhd M$
such that
![]() $f:\rho \rightarrow \rho ^{+M}$
is cofinal. But then there is also
$f:\rho \rightarrow \rho ^{+M}$
is cofinal. But then there is also
![]() $f^{\prime }:\rho \rightarrow \rho ^{+M}$
onto and
$f^{\prime }:\rho \rightarrow \rho ^{+M}$
onto and
![]() $f^{\prime }\in J(M\vert \gamma )$
. Contradiction!
$f^{\prime }\in J(M\vert \gamma )$
. Contradiction!
Let us suppose now that
![]() $\xi <\rho ^{+M}$
. Note that since
$\xi <\rho ^{+M}$
. Note that since
![]() $\text {Hull}_{1}^{M}(\rho \cup \{p_{1}^{M}\})\subset H^{\prime }$
and
$\text {Hull}_{1}^{M}(\rho \cup \{p_{1}^{M}\})\subset H^{\prime }$
and
![]() $\text {Hull}_{1}^{M}(\rho \cup \{p_{1}^{M}\})$
is unbounded in
$\text {Hull}_{1}^{M}(\rho \cup \{p_{1}^{M}\})$
is unbounded in
![]() $\operatorname {\mathrm {OR}}^{M}$
,
$\operatorname {\mathrm {OR}}^{M}$
,
![]() $H^{\prime }$
is unbounded in
$H^{\prime }$
is unbounded in
![]() $\operatorname {\mathrm {OR}}^{M}$
. Again we have that
$\operatorname {\mathrm {OR}}^{M}$
. Again we have that
Thus, by
![]() $\Delta _{0}$
-collection there is some
$\Delta _{0}$
-collection there is some
![]() $\gamma <\operatorname {\mathrm {OR}}^{M}$
such that
$\gamma <\operatorname {\mathrm {OR}}^{M}$
such that
Since
![]() $H^{\prime }$
is unbounded in
$H^{\prime }$
is unbounded in
![]() $\operatorname {\mathrm {OR}}^{M}$
, there is some such
$\operatorname {\mathrm {OR}}^{M}$
, there is some such
![]() $\gamma \in H^{\prime }$
. But then since
$\gamma \in H^{\prime }$
. But then since
![]() $\rho \in H^{\prime }$
there is
$\rho \in H^{\prime }$
there is
![]() $f\in H^{\prime }$
such that
$f\in H^{\prime }$
such that
![]() $f:\rho \rightarrow \xi $
is cofinal and thus also some
$f:\rho \rightarrow \xi $
is cofinal and thus also some
![]() $f^{\prime }:\rho \rightarrow \xi $
which is surjective and
$f^{\prime }:\rho \rightarrow \xi $
which is surjective and
![]() $f^{\prime }\in H^{\prime }$
. But this means that
$f^{\prime }\in H^{\prime }$
. But this means that
![]() $\xi \in H^{\prime }$
. Contradiction!
$\xi \in H^{\prime }$
. Contradiction!
2.1 Forcing over admissible premice
In this subsection, we will prove that if M is an admissible passive premouse with a largest cardinal
![]() $\delta $
which is Woodin in M,
$\delta $
which is Woodin in M,
![]() $\mathbb {B}$
is the extender algebra as defined inside M, and
$\mathbb {B}$
is the extender algebra as defined inside M, and
![]() $g\subset \mathbb {B}$
is M-generic, then
$g\subset \mathbb {B}$
is M-generic, then
![]() $M[g]\models \text {KP}$
. This will be Corollary 11 which is an instance of the more general Theorem 10.
$M[g]\models \text {KP}$
. This will be Corollary 11 which is an instance of the more general Theorem 10.
Note that if M is an admissible passive premouse with a largest, regular, and uncountable cardinal
![]() $\delta $
and
$\delta $
and
![]() $\mathbb {P}\in M$
is a forcing poset, then we may assume without loss of generality that
$\mathbb {P}\in M$
is a forcing poset, then we may assume without loss of generality that
![]() $\mathbb {P}\subset \delta $
, as there is a surjection
$\mathbb {P}\subset \delta $
, as there is a surjection
![]() $f:\delta \rightarrow \mathbb {P}$
in M. We will do so throughout without further mention.
$f:\delta \rightarrow \mathbb {P}$
in M. We will do so throughout without further mention.
Lemma 5. Let M be an admissible passive premouse with a largest, regular, and uncountable cardinal
![]() $\delta $
and let
$\delta $
and let
![]() $\mathbb {P}\in M$
be a forcing poset such that
$\mathbb {P}\in M$
be a forcing poset such that
![]() ${M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}"}$
Then there is no
${M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}"}$
Then there is no
![]() $A\in \Sigma _{1}^{M}(M)$
such that
$A\in \Sigma _{1}^{M}(M)$
such that
![]() $A\subset \mathbb {P}$
is an antichain in
$A\subset \mathbb {P}$
is an antichain in
![]() $\mathbb {P}$
which is unbounded in
$\mathbb {P}$
which is unbounded in
![]() $\delta $
.
$\delta $
.
Proof. Suppose there is
![]() $A\in \Sigma _{1}^{M}(M)$
is such that
$A\in \Sigma _{1}^{M}(M)$
is such that
![]() $A\subset \mathbb {P}$
is an antichain in
$A\subset \mathbb {P}$
is an antichain in
![]() $\mathbb {P}$
which is unbounded in
$\mathbb {P}$
which is unbounded in
![]() $\delta $
. Since
$\delta $
. Since
![]() $\mathbb {P}$
has the
$\mathbb {P}$
has the
![]() $\delta $
-c.c. in M, and
$\delta $
-c.c. in M, and
![]() $\delta $
is regular in M, this means that
$\delta $
is regular in M, this means that
![]() $A\notin M$
. Let
$A\notin M$
. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Sigma _{1}$
-formula such that for some
$\Sigma _{1}$
-formula such that for some
![]() $p\in M$
,
$p\in M$
,
Define for
![]() $\alpha <\operatorname {\mathrm {OR}}^{M}\setminus \delta $
such that
$\alpha <\operatorname {\mathrm {OR}}^{M}\setminus \delta $
such that
![]() $p\in M\vert \alpha $
,
$p\in M\vert \alpha $
,
Note that
![]() $A=\bigcup _{\alpha <\operatorname {\mathrm {OR}}^{M}}A_{\alpha }$
and
$A=\bigcup _{\alpha <\operatorname {\mathrm {OR}}^{M}}A_{\alpha }$
and
![]() $A_{\alpha }\in M$
for all
$A_{\alpha }\in M$
for all
![]() $\alpha $
such that
$\alpha $
such that
![]() $\alpha \in \operatorname {\mathrm {OR}}^{M}\setminus \delta $
and
$\alpha \in \operatorname {\mathrm {OR}}^{M}\setminus \delta $
and
![]() ${p\in M\vert \alpha} $
. In particular, since
${p\in M\vert \alpha} $
. In particular, since
![]() $A_{\alpha }\subset A$
is an antichain,
$A_{\alpha }\subset A$
is an antichain,
![]() $\mathbb {P}$
has the
$\mathbb {P}$
has the
![]() $\delta $
-c.c. in M, and
$\delta $
-c.c. in M, and
![]() $\delta $
is regular in M,
$\delta $
is regular in M,
![]() $A_{\alpha }$
is bounded in
$A_{\alpha }$
is bounded in
![]() $\delta $
for all such
$\delta $
for all such
![]() $\alpha $
.
$\alpha $
.
Note that since
![]() $A=\bigcup _{\alpha <\operatorname {\mathrm {OR}}^{M}}A_{\alpha }$
is by assumption unbounded in
$A=\bigcup _{\alpha <\operatorname {\mathrm {OR}}^{M}}A_{\alpha }$
is by assumption unbounded in
![]() $\delta $
,
$\delta $
,
Since the last part of this formula is
![]() $\Sigma _{1}$
, we have by
$\Sigma _{1}$
, we have by
![]() $\Delta _{0}$
-collection that there is some
$\Delta _{0}$
-collection that there is some
![]() $\alpha ^{\prime }\in M$
such that
$\alpha ^{\prime }\in M$
such that
![]() $\alpha ^{\prime }$
works for all
$\alpha ^{\prime }$
works for all
![]() $\beta <\delta $
uniformly, i.e.
$\beta <\delta $
uniformly, i.e.
This contradicts the fact that every
![]() $A_\alpha $
is bounded in
$A_\alpha $
is bounded in
![]() $\delta $
!
$\delta $
!
Lemma 6. Suppose that M is an admissible passive premouse with a largest, regular, and uncountable cardinal
![]() $\delta $
. Then
$\delta $
. Then
![]() $\delta $
is a
$\delta $
is a
![]() $\Sigma _{1}^{M}(M)$
-regular cardinal, i.e. for all
$\Sigma _{1}^{M}(M)$
-regular cardinal, i.e. for all
![]() $\eta <\delta $
and
$\eta <\delta $
and
![]() $f\in \Sigma _{1}^{M}(M)$
such that
$f\in \Sigma _{1}^{M}(M)$
such that
![]() $f:\eta \rightarrow \delta $
,
$f:\eta \rightarrow \delta $
,
![]() $\operatorname {\mathrm {ran}}(f)$
is bounded in
$\operatorname {\mathrm {ran}}(f)$
is bounded in
![]() $\delta $
, i.e.,
$\delta $
, i.e.,
![]() $\sup (\operatorname {\mathrm {ran}}(f))<\delta $
.
$\sup (\operatorname {\mathrm {ran}}(f))<\delta $
.
The proof of the Lemma is very similar to the proof of Lemma 5. Thus, we leave it as an exercise for the reader.
Definition 7. Let M be an admissible passive premouse,
![]() $\mathbb {P}\in M$
be a forcing poset, and
$\mathbb {P}\in M$
be a forcing poset, and
![]() $g\subset \mathbb {P}$
be M-generic. Let
$g\subset \mathbb {P}$
be M-generic. Let
![]() $\xi < \operatorname {\mathrm {OR}}^M$
such that
$\xi < \operatorname {\mathrm {OR}}^M$
such that
![]() $\mathbb {P} \in M \vert \xi +1$
. For
$\mathbb {P} \in M \vert \xi +1$
. For
![]() $\beta \geq \omega \cdot \xi $
it is a standard fact that
$\beta \geq \omega \cdot \xi $
it is a standard fact that
![]() $\Vdash _{M\vert \vert \beta }^{\mathbb {P}}\in M$
, where
$\Vdash _{M\vert \vert \beta }^{\mathbb {P}}\in M$
, where
![]() $\Vdash _{M\vert \vert \beta }^{\mathbb {P}}$
is the syntactical forcing relation with
$\Vdash _{M\vert \vert \beta }^{\mathbb {P}}$
is the syntactical forcing relation with
![]() $M\vert \vert \beta $
as a ground model using
$M\vert \vert \beta $
as a ground model using
![]() $\mathbb {P}$
-names in
$\mathbb {P}$
-names in
![]() $M \vert \vert \beta $
. Moreover, the function F is
$M \vert \vert \beta $
. Moreover, the function F is
![]() $\Delta _{1}^{M}(\{\mathbb {P}\})$
, where
$\Delta _{1}^{M}(\{\mathbb {P}\})$
, where
![]() $F(\beta )= {\Vdash }_{M\vert \vert \beta }^{\mathbb {P}}$
for
$F(\beta )= {\Vdash }_{M\vert \vert \beta }^{\mathbb {P}}$
for
![]() $\beta \geq \omega \cdot \xi $
. We let
$\beta \geq \omega \cdot \xi $
. We let
![]() $M[g] \vert \vert \beta = (L_\beta [\mathbb {E}^M, g], \in , \mathbb {E}^M \!\upharpoonright \! \beta ,g)$
and have that
$M[g] \vert \vert \beta = (L_\beta [\mathbb {E}^M, g], \in , \mathbb {E}^M \!\upharpoonright \! \beta ,g)$
and have that
![]() $\lfloor M[g] \vert \vert \beta \rfloor $
is the collection of the evaluations of the
$\lfloor M[g] \vert \vert \beta \rfloor $
is the collection of the evaluations of the
![]() $\mathbb {P}$
-names in
$\mathbb {P}$
-names in
![]() $M \vert \vert \beta $
. We let
$M \vert \vert \beta $
. We let
![]() $M \vert \vert \beta [g] = M[g]\vert \vert \beta $
.Footnote
4
$M \vert \vert \beta [g] = M[g]\vert \vert \beta $
.Footnote
4
Suppose that
![]() $g\subset \mathbb {P}$
is M-generic and that for a
$g\subset \mathbb {P}$
is M-generic and that for a
![]() $\Sigma _{0}$
-formula
$\Sigma _{0}$
-formula
![]() $\psi $
,
$\psi $
,
![]() $M[g]\models \exists x\psi (x,z_{1},...,z_{n})$
, where
$M[g]\models \exists x\psi (x,z_{1},...,z_{n})$
, where
![]() $\{z_{1},...,z_{n}\}\subset M[g]$
. Let
$\{z_{1},...,z_{n}\}\subset M[g]$
. Let
![]() $\varphi \equiv \exists x\psi $
be the corresponding
$\varphi \equiv \exists x\psi $
be the corresponding
![]() $\Sigma _{1}$
formula and let
$\Sigma _{1}$
formula and let
![]() $\dot {z}_{1},...,\dot {z}_{n}$
be
$\dot {z}_{1},...,\dot {z}_{n}$
be
![]() $\mathbb {P}$
-names for
$\mathbb {P}$
-names for
![]() $z_{1},...,z_{n}$
. We let
$z_{1},...,z_{n}$
. We let
We call the set
![]() $W_{\varphi ,\dot {z}_{1},...,\dot {z}_{n}}^{M}$
the set of conditions strongly forcing
$W_{\varphi ,\dot {z}_{1},...,\dot {z}_{n}}^{M}$
the set of conditions strongly forcing
![]() $\varphi $
(with parameters
$\varphi $
(with parameters
![]() $\dot {z}_{1},...,\dot {z}_{n}$
).Footnote
5
$\dot {z}_{1},...,\dot {z}_{n}$
).Footnote
5
Remark. Since
![]() $M\models "\text {Pairing}"$
it follows easily (using
$M\models "\text {Pairing}"$
it follows easily (using
![]() $\mathbb {P}$
-names) that
$\mathbb {P}$
-names) that
![]() $M[g]\models "\text {Pairing}"$
. Therefore, we may arrange that n has any specific value which we want it to have. In particular,
$M[g]\models "\text {Pairing}"$
. Therefore, we may arrange that n has any specific value which we want it to have. In particular,
![]() $1$
.
$1$
.
We will write
![]() $W_{\varphi ,\dot {z}_{1},...,\dot {z}_{n}}$
for
$W_{\varphi ,\dot {z}_{1},...,\dot {z}_{n}}$
for
![]() $W_{\varphi ,\dot {z}_{1},...,\dot {z}_{n}}^{M}$
if it is clear from the context what M is. Since
$W_{\varphi ,\dot {z}_{1},...,\dot {z}_{n}}^{M}$
if it is clear from the context what M is. Since
![]() $F\in \Delta _{1}^{M}(\{\mathbb {P}\})$
, it follows easily that
$F\in \Delta _{1}^{M}(\{\mathbb {P}\})$
, it follows easily that
![]() $W_{\varphi ,\dot {z}}\in \Sigma _{1}^{M}(\{\dot {z},\varphi ,\mathbb {P}\})$
. Moreover, since
$W_{\varphi ,\dot {z}}\in \Sigma _{1}^{M}(\{\dot {z},\varphi ,\mathbb {P}\})$
. Moreover, since
![]() $\mathbb {P}\in M$
, there is
$\mathbb {P}\in M$
, there is
![]() $\beta <\operatorname {\mathrm {OR}}^{M}$
such that
$\beta <\operatorname {\mathrm {OR}}^{M}$
such that
![]() $\mathbb {P}\in M\vert \beta $
so that
$\mathbb {P}\in M\vert \beta $
so that
![]() $W_{\varphi ,\dot {z}}$
is not trivially empty. However, in general we cannot assume that
$W_{\varphi ,\dot {z}}$
is not trivially empty. However, in general we cannot assume that
![]() $W_{\varphi ,\dot {z}}\in M$
.
$W_{\varphi ,\dot {z}}\in M$
.
We also write
![]() $p\Vdash _{M}^{w.\mathbb {P}}\varphi (\dot {z})$
for
$p\Vdash _{M}^{w.\mathbb {P}}\varphi (\dot {z})$
for
![]() $p\in W_{\varphi ,\dot {z}}$
.
$p\in W_{\varphi ,\dot {z}}$
.
For
![]() $\beta < \operatorname {\mathrm {OR}}^M$
we might interpret the
$\beta < \operatorname {\mathrm {OR}}^M$
we might interpret the
![]() $\Sigma _1$
formula defining
$\Sigma _1$
formula defining
![]() $W_{\varphi ,\dot {z}}$
over the structure
$W_{\varphi ,\dot {z}}$
over the structure
![]() $M \vert \beta $
. We will denote the set defined over
$M \vert \beta $
. We will denote the set defined over
![]() $M \vert \beta $
in this way by
$M \vert \beta $
in this way by
![]() $W_{\varphi ,\dot {z}}^{M \vert \beta }$
.
$W_{\varphi ,\dot {z}}^{M \vert \beta }$
.
We have the following forcing theorem for
![]() $\Sigma _{1}$
statements for admissible premice.
$\Sigma _{1}$
statements for admissible premice.
Theorem 8. Suppose that M is an admissible passive premouse. Let
![]() $\varphi (y)$
be the formula
$\varphi (y)$
be the formula
![]() $\exists x\psi (x,y)$
, where
$\exists x\psi (x,y)$
, where
![]() $\psi $
is a
$\psi $
is a
![]() $\Sigma _{0}$
formula. Let
$\Sigma _{0}$
formula. Let
![]() $\mathbb {P}\in M$
be a forcing poset,
$\mathbb {P}\in M$
be a forcing poset,
![]() $\dot {z} \in M^{\mathbb {P}}$
, and suppose that
$\dot {z} \in M^{\mathbb {P}}$
, and suppose that
![]() $g\subset \mathbb {P}$
is M-generic. Then the following are equivalent:
$g\subset \mathbb {P}$
is M-generic. Then the following are equivalent:
-
•
 $M[g]\models \varphi (\dot {z}^{g})$
,
$M[g]\models \varphi (\dot {z}^{g})$
, -
• there is
 $p\in W_{\varphi ,\dot {z}}\cap g$
, and
$p\in W_{\varphi ,\dot {z}}\cap g$
, and -
• there is
 $p\in g$
such that
$p\in g$
such that
 $p\Vdash _{M}^{\mathbb {P}}\varphi (\dot {z})$
.
$p\Vdash _{M}^{\mathbb {P}}\varphi (\dot {z})$
.
Remark. Here
![]() $p\Vdash _{M}^{\mathbb {P}}\varphi (\dot {z})$
refers to the classical notion of forcing an existential statement, i.e., for every
$p\Vdash _{M}^{\mathbb {P}}\varphi (\dot {z})$
refers to the classical notion of forcing an existential statement, i.e., for every
![]() $q\leq p$
there is some
$q\leq p$
there is some
![]() $r\leq q$
such that there is
$r\leq q$
such that there is
![]() $\dot {x}\in M^{\mathbb {P}}$
such that
$\dot {x}\in M^{\mathbb {P}}$
such that
![]() $r\Vdash _{M}^{\mathbb {P}}\psi (\dot {x},\dot {z})$
. In order to show that this is equivalent to the existence of some
$r\Vdash _{M}^{\mathbb {P}}\psi (\dot {x},\dot {z})$
. In order to show that this is equivalent to the existence of some
![]() $p\in W_{\varphi ,\dot {z}}\cap g$
, we must use the admissibility of M. The rest of the proof is standard.
$p\in W_{\varphi ,\dot {z}}\cap g$
, we must use the admissibility of M. The rest of the proof is standard.
It is not in general the case that if N is admissible and
![]() $g\subset \mathbb {P}$
is N-generic for some forcing poset
$g\subset \mathbb {P}$
is N-generic for some forcing poset
![]() $\mathbb {P}\in N$
, then
$\mathbb {P}\in N$
, then
![]() $N[g]$
is admissible. See Proposition 13 and the remark preceding it for examples of admissible structures where the generic extension fails to be admissible. For
$N[g]$
is admissible. See Proposition 13 and the remark preceding it for examples of admissible structures where the generic extension fails to be admissible. For
![]() $N[g]$
to be admissible, it is sufficient that g meets all dense open subsets of
$N[g]$
to be admissible, it is sufficient that g meets all dense open subsets of
![]() $\mathbb {P}$
that are unions of a
$\mathbb {P}$
that are unions of a
![]() $\Sigma _{1}^N(N)$
and a
$\Sigma _{1}^N(N)$
and a
![]() $\Pi _{1}^N (N)$
class over N. See [Reference Mathias5] for more on this. With Theorem 10 we will give another criterion for ensuring that the forcing extension of an admissible premouse is a model of KP.
$\Pi _{1}^N (N)$
class over N. See [Reference Mathias5] for more on this. With Theorem 10 we will give another criterion for ensuring that the forcing extension of an admissible premouse is a model of KP.
Lemma 9. Let M be an admissible passive premouse with a largest, regular, and uncountable cardinal
![]() $\delta $
. Let
$\delta $
. Let
![]() $\mathbb {P}\in M$
be a forcing such that
$\mathbb {P}\in M$
be a forcing such that
![]() $M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}"$
. Let
$M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}"$
. Let
![]() $g\subset \mathbb {P}$
be M-generic. Let
$g\subset \mathbb {P}$
be M-generic. Let
![]() $\lambda <\delta $
and suppose that
$\lambda <\delta $
and suppose that
![]() $M[g]\models \forall \alpha <\lambda \exists x\psi (x,\alpha ,z)$
, where
$M[g]\models \forall \alpha <\lambda \exists x\psi (x,\alpha ,z)$
, where
![]() $\psi $
is a
$\psi $
is a
![]() $\Sigma _{0}$
-formula and
$\Sigma _{0}$
-formula and
![]() $z\in M[g]$
. Let
$z\in M[g]$
. Let
![]() $\varphi \equiv \exists x\psi $
and
$\varphi \equiv \exists x\psi $
and
![]() $\dot {z}\in M^{\mathbb {P}}$
be a name for z.
$\dot {z}\in M^{\mathbb {P}}$
be a name for z.
Then there is
![]() $A\in M$
such that
$A\in M$
such that
![]() $A\subset \lambda \times \delta $
and if for
$A\subset \lambda \times \delta $
and if for
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $A_{\alpha }:=\{\beta :(\alpha ,\beta )\in A\}$
, then
$A_{\alpha }:=\{\beta :(\alpha ,\beta )\in A\}$
, then
![]() $A_{\alpha }\subset W_{\varphi ,\check {\alpha },\dot {z}}$
is a maximal antichain in
$A_{\alpha }\subset W_{\varphi ,\check {\alpha },\dot {z}}$
is a maximal antichain in
![]() $W_{\varphi ,\check {\alpha },\dot {z}}$
, in particular, for every
$W_{\varphi ,\check {\alpha },\dot {z}}$
, in particular, for every
![]() $p\in W_{\varphi ,\check {\alpha },\dot {z}}$
there is some
$p\in W_{\varphi ,\check {\alpha },\dot {z}}$
there is some
![]() $q\in A_{\alpha }$
such that
$q\in A_{\alpha }$
such that
![]() $q\mid \mid p$
.
$q\mid \mid p$
.
Proof. We construct the set A recursively along the ordinals of M. More specifically, we will define via a
![]() $\Sigma _{1}$
-recursion a sequence
$\Sigma _{1}$
-recursion a sequence
![]() $\langle (A^{i},\beta _{i}):i<\operatorname {\mathrm {OR}}^{M}\rangle $
with each
$\langle (A^{i},\beta _{i}):i<\operatorname {\mathrm {OR}}^{M}\rangle $
with each
![]() $A^i \in M$
and
$A^i \in M$
and
![]() $\beta _i \in \operatorname {\mathrm {OR}}^M$
, and
$\beta _i \in \operatorname {\mathrm {OR}}^M$
, and
![]() $\langle (A^i,\beta _i) : i< \lambda \rangle \in M$
for each
$\langle (A^i,\beta _i) : i< \lambda \rangle \in M$
for each
![]() $\lambda <\operatorname {\mathrm {OR}}^M$
. We will then set
$\lambda <\operatorname {\mathrm {OR}}^M$
. We will then set
![]() $A=\bigcup _{i<\operatorname {\mathrm {OR}}^{M}}A^{i}$
. Let
$A=\bigcup _{i<\operatorname {\mathrm {OR}}^{M}}A^{i}$
. Let
![]() $\beta _{0}$
be the least
$\beta _{0}$
be the least
![]() $\beta $
such that
$\beta $
such that
i.e.,
![]() $\beta $
is such that there is some
$\beta $
is such that there is some
![]() $\alpha <\lambda $
such that
$\alpha <\lambda $
such that
![]() $W_{\varphi ,\check {\alpha },\dot {z}}^{ M\vert \beta }\neq \emptyset $
. Let
$W_{\varphi ,\check {\alpha },\dot {z}}^{ M\vert \beta }\neq \emptyset $
. Let
![]() $A^{0}$
be the set of all
$A^{0}$
be the set of all
![]() $(\alpha ,p)\in A^{0}$
such that
$(\alpha ,p)\in A^{0}$
such that
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $W_{\varphi ,\check {\alpha },\dot {z}}^{M\vert \beta _0} \neq \emptyset $
, and p is the
$W_{\varphi ,\check {\alpha },\dot {z}}^{M\vert \beta _0} \neq \emptyset $
, and p is the
![]() $<_{M}$
-least element in
$<_{M}$
-least element in
![]() $W_{\varphi ,\check {\alpha },\dot {z}}^{M\vert \beta _0}$
. Here,
$W_{\varphi ,\check {\alpha },\dot {z}}^{M\vert \beta _0}$
. Here,
![]() $<_{M}$
denotes the canonical
$<_{M}$
denotes the canonical
![]() $\Sigma _{1}$
-definable well-order of M. Note that
$\Sigma _{1}$
-definable well-order of M. Note that
![]() $A^{0}\in M$
, since it is definable over
$A^{0}\in M$
, since it is definable over
![]() $M \vert \beta _0$
. Moreover,
$M \vert \beta _0$
. Moreover,
![]() $A^{0}$
is a bounded subset of
$A^{0}$
is a bounded subset of
![]() $\delta $
. (Actually, of
$\delta $
. (Actually, of
![]() $\delta ^{2}$
, but via coding we may assume that
$\delta ^{2}$
, but via coding we may assume that
![]() $A^{0}\subset \delta $
). Before we continue the construction let us introduce the following notation: For
$A^{0}\subset \delta $
). Before we continue the construction let us introduce the following notation: For
![]() $\alpha <\lambda $
and
$\alpha <\lambda $
and
![]() $i<\operatorname {\mathrm {OR}}^{M}$
let
$i<\operatorname {\mathrm {OR}}^{M}$
let
![]() $A_{\alpha }^{i}:=\{q\in \mathbb {P}:(\alpha ,q)\in A^{i}\}$
, where
$A_{\alpha }^{i}:=\{q\in \mathbb {P}:(\alpha ,q)\in A^{i}\}$
, where
![]() $A^{i}$
is to be defined.
$A^{i}$
is to be defined.
Let
![]() $\gamma +1<\operatorname {\mathrm {OR}}^{M}$
and suppose that
$\gamma +1<\operatorname {\mathrm {OR}}^{M}$
and suppose that
![]() $\langle (A^{i},\beta _{i}):i\leq \gamma \rangle $
is defined such that
$\langle (A^{i},\beta _{i}):i\leq \gamma \rangle $
is defined such that
![]() $\langle (A^{i},\beta _{i}):i\leq \gamma \rangle \in \Sigma _{1}^{M}(\{\lambda ,\psi ,\dot {z},\mathbb {P}\})$
. We define
$\langle (A^{i},\beta _{i}):i\leq \gamma \rangle \in \Sigma _{1}^{M}(\{\lambda ,\psi ,\dot {z},\mathbb {P}\})$
. We define
![]() $\beta _{\gamma +1}$
as the least
$\beta _{\gamma +1}$
as the least
![]() $\beta $
such that
$\beta $
such that
if there is such
![]() $\beta $
. In other words
$\beta $
. In other words
![]() $\beta $
is such that for some
$\beta $
is such that for some
![]() $\alpha $
there is an element
$\alpha $
there is an element
![]() $p\in W_{\varphi ,\check {\alpha },\dot {z}}^{M\vert \beta }$
incompatible with the elements of
$p\in W_{\varphi ,\check {\alpha },\dot {z}}^{M\vert \beta }$
incompatible with the elements of
![]() $A_{\alpha }^{\gamma }$
. In case
$A_{\alpha }^{\gamma }$
. In case
![]() $\beta _{\gamma +1}$
is undefined we stop the recursion. Note that in this case
$\beta _{\gamma +1}$
is undefined we stop the recursion. Note that in this case
![]() $A^{\gamma }\in M$
.
$A^{\gamma }\in M$
.
In case
![]() $\beta _{\gamma +1}$
is defined, we set
$\beta _{\gamma +1}$
is defined, we set
![]() $A^{\gamma +1}$
to be the union of
$A^{\gamma +1}$
to be the union of
![]() $A^{\gamma }$
with the set of all
$A^{\gamma }$
with the set of all
![]() $(\alpha ,p)$
such that p is the
$(\alpha ,p)$
such that p is the
![]() $<_{M}$
-least q such that
$<_{M}$
-least q such that
if there is such q. Since
![]() $A^{\gamma +1}$
is definable over
$A^{\gamma +1}$
is definable over
![]() $M\vert \beta _{\gamma +1}$
,
$M\vert \beta _{\gamma +1}$
,
![]() $A^{\gamma +1}\in M$
.
$A^{\gamma +1}\in M$
.
Now suppose that
![]() $\gamma <\operatorname {\mathrm {OR}}^{M}$
is a limit ordinal and
$\gamma <\operatorname {\mathrm {OR}}^{M}$
is a limit ordinal and
![]() $\langle A^{i}:i<\gamma \rangle $
is defined. We set
$\langle A^{i}:i<\gamma \rangle $
is defined. We set
![]() $\beta _{\gamma }=0$
and
$\beta _{\gamma }=0$
and
![]() $A^{\gamma }=\bigcup _{i<\gamma }A^{i}$
. Note that since
$A^{\gamma }=\bigcup _{i<\gamma }A^{i}$
. Note that since
![]() $\langle A_{i}:i<\gamma \rangle \in \Sigma _{1}^{M}(M)$
by KP,
$\langle A_{i}:i<\gamma \rangle \in \Sigma _{1}^{M}(M)$
by KP,
![]() $A^{\gamma }\in M$
.
$A^{\gamma }\in M$
.
We aim to see that the recursive definition of
![]() $\langle (A^{i},\beta _{i}):i<\operatorname {\mathrm {OR}}^{M}\rangle $
stops before the ordinal height of
$\langle (A^{i},\beta _{i}):i<\operatorname {\mathrm {OR}}^{M}\rangle $
stops before the ordinal height of
![]() $\operatorname {\mathrm {OR}}^{M}$
, i.e. there is some
$\operatorname {\mathrm {OR}}^{M}$
, i.e. there is some
![]() $\gamma <\operatorname {\mathrm {OR}}^{M}$
such that
$\gamma <\operatorname {\mathrm {OR}}^{M}$
such that
![]() $\beta _{\gamma }$
is not defined. Suppose that this is not the case. We claim that
$\beta _{\gamma }$
is not defined. Suppose that this is not the case. We claim that
![]() $\bar {A}:=\bigcup _{i<\operatorname {\mathrm {OR}}^{M}}A^{i}\in \Sigma _{1}^{M}(M)$
is an unbounded subset of
$\bar {A}:=\bigcup _{i<\operatorname {\mathrm {OR}}^{M}}A^{i}\in \Sigma _{1}^{M}(M)$
is an unbounded subset of
![]() $\delta $
. For suppose not. Then, since
$\delta $
. For suppose not. Then, since
![]() $\rho _{1}^{M}=\delta $
,
$\rho _{1}^{M}=\delta $
,
![]() $\bar {A}\in M$
. But the definition of
$\bar {A}\in M$
. But the definition of
![]() $\bar {A}$
gives a cofinal and total
$\bar {A}$
gives a cofinal and total
![]() $f:\bar {A}\rightarrow \operatorname {\mathrm {OR}}^{M}$
such that
$f:\bar {A}\rightarrow \operatorname {\mathrm {OR}}^{M}$
such that
![]() $f\in \Sigma _{1}^{M}(M)$
. Contradiction!
$f\in \Sigma _{1}^{M}(M)$
. Contradiction!
In particular, the following holds in M,
But by
![]() $\Delta _{0}$
-collection, there is some
$\Delta _{0}$
-collection, there is some
![]() $\beta _{i}<\operatorname {\mathrm {OR}}^{M}$
such that for all
$\beta _{i}<\operatorname {\mathrm {OR}}^{M}$
such that for all
![]() $\beta <\delta $
, there is some
$\beta <\delta $
, there is some
![]() $\gamma \in (\beta ,\delta )$
added to
$\gamma \in (\beta ,\delta )$
added to
![]() $A_{\alpha }^{i}$
for some
$A_{\alpha }^{i}$
for some
![]() $\alpha <\lambda $
. But this is inside
$\alpha <\lambda $
. But this is inside
![]() $M\vert \beta _{i}+\omega $
. Thus, as
$M\vert \beta _{i}+\omega $
. Thus, as
![]() $\delta $
is a regular cardinal of M, there is some
$\delta $
is a regular cardinal of M, there is some
![]() $\alpha $
to which unboundedly many
$\alpha $
to which unboundedly many
![]() $\gamma <\delta $
are added. Contradiction, since
$\gamma <\delta $
are added. Contradiction, since
![]() $\mathbb {P}$
has the
$\mathbb {P}$
has the
![]() $\delta $
-c.c. in M.
$\delta $
-c.c. in M.
Let
![]() $\gamma <\operatorname {\mathrm {OR}}^{M}$
be least such that
$\gamma <\operatorname {\mathrm {OR}}^{M}$
be least such that
![]() $\beta _{\gamma }$
is undefined. Note that
$\beta _{\gamma }$
is undefined. Note that
![]() $\gamma $
is by definition a successor ordinal, i.e.
$\gamma $
is by definition a successor ordinal, i.e.
![]() $\gamma =\eta +1$
for some
$\gamma =\eta +1$
for some
![]() $\eta <\operatorname {\mathrm {OR}}^{M}$
. Set
$\eta <\operatorname {\mathrm {OR}}^{M}$
. Set
![]() $A:=A^{\eta }$
. By construction
$A:=A^{\eta }$
. By construction
![]() $A\in M$
. For
$A\in M$
. For
![]() $\alpha <\lambda $
, set
$\alpha <\lambda $
, set
![]() $A_{\alpha }:=\{p\in \mathbb {P}:(\alpha ,p)\in A\}$
. Since
$A_{\alpha }:=\{p\in \mathbb {P}:(\alpha ,p)\in A\}$
. Since
![]() $\beta _{\eta +1}$
is undefined, we have that for all
$\beta _{\eta +1}$
is undefined, we have that for all
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $A_{\alpha }\subset W_{\varphi ,\check {\alpha },\dot {z}}$
is a maximal antichain in
$A_{\alpha }\subset W_{\varphi ,\check {\alpha },\dot {z}}$
is a maximal antichain in
![]() $W_{\varphi ,\check {\alpha },\dot {z}}$
.
$W_{\varphi ,\check {\alpha },\dot {z}}$
.
Theorem 10. Let M be an admissible passive premouse with a largest, regular, and uncountable cardinal
![]() $\delta $
and
$\delta $
and
![]() $\mathbb {P}\in M$
be such that
$\mathbb {P}\in M$
be such that
![]() $M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}"$
Then
$M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}"$
Then
![]() $M[g]\models \text {KP}$
for any M-generic
$M[g]\models \text {KP}$
for any M-generic
![]() $g\subset \mathbb {P}$
.
$g\subset \mathbb {P}$
.
Proof. We will verify that
![]() $M[g]$
satisfies
$M[g]$
satisfies
![]() $\Delta _{0}$
-collection and leave the remaining axioms of KP as an exercise.
$\Delta _{0}$
-collection and leave the remaining axioms of KP as an exercise.
Let
![]() $g\subset \mathbb {P}$
be M-generic and suppose for the sake of contradiction that
$g\subset \mathbb {P}$
be M-generic and suppose for the sake of contradiction that
![]() $M[g]\not \models "\Delta _{0}\text {-collection}"$
. Let
$M[g]\not \models "\Delta _{0}\text {-collection}"$
. Let
![]() $\psi $
be a
$\psi $
be a
![]() $\Sigma _{0}$
-formula and
$\Sigma _{0}$
-formula and
![]() $y\in M[g]$
such that they constitute a counterexample to
$y\in M[g]$
such that they constitute a counterexample to
![]() $\Delta _{0}$
-collection, i.e.
$\Delta _{0}$
-collection, i.e.
but there exists no
![]() $z\in M[g]$
such that
$z\in M[g]$
such that
We distinguish two cases. First, suppose that there is some
![]() $\lambda <\delta $
such that there exists no
$\lambda <\delta $
such that there exists no
![]() $z\in M[g]$
such that
$z\in M[g]$
such that
Then, by the previous Lemma 9 there is
![]() $A\in M$
such that for
$A\in M$
such that for
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $A_{\alpha }:=\{p\in \mathbb {P}:(\alpha ,p)\in A\}$
is a maximal antichain in
$A_{\alpha }:=\{p\in \mathbb {P}:(\alpha ,p)\in A\}$
is a maximal antichain in
![]() $W_{\varphi ,\check {\alpha },\dot {y}}$
, where
$W_{\varphi ,\check {\alpha },\dot {y}}$
, where
![]() $\varphi \equiv \exists x\psi $
and
$\varphi \equiv \exists x\psi $
and
![]() $\dot {y}\in M^{\mathbb {P}}$
is a
$\dot {y}\in M^{\mathbb {P}}$
is a
![]() $\mathbb {P}$
-name for y.
$\mathbb {P}$
-name for y.
Claim 1. For
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $A_{\alpha }\cap g\neq \emptyset $
.
$A_{\alpha }\cap g\neq \emptyset $
.
Proof. Fix some
![]() $\alpha <\lambda $
. Note that since
$\alpha <\lambda $
. Note that since
![]() $M[g]\models \exists x\psi (\alpha ,x,y)$
, there is some
$M[g]\models \exists x\psi (\alpha ,x,y)$
, there is some
![]() ${b\in M[g]}$
such that
${b\in M[g]}$
such that
![]() $M[g]\models \psi (\alpha ,b,y)$
. By Theorem 8 we can fix some
$M[g]\models \psi (\alpha ,b,y)$
. By Theorem 8 we can fix some
![]() $p\in g\cap W_{\varphi ,\check {\alpha },\dot {y}}$
. We claim that this implies that
$p\in g\cap W_{\varphi ,\check {\alpha },\dot {y}}$
. We claim that this implies that
![]() $A_{\alpha }\cap g\neq \emptyset $
. To this end let
$A_{\alpha }\cap g\neq \emptyset $
. To this end let
![]() $D_{\alpha }:=\{r\in \mathbb {P}:\forall q\in A_{\alpha }(r\perp q)\}$
. Note that since
$D_{\alpha }:=\{r\in \mathbb {P}:\forall q\in A_{\alpha }(r\perp q)\}$
. Note that since
![]() $A_{\alpha }\in M$
,
$A_{\alpha }\in M$
,
![]() $D_{\alpha }\in M$
. Moreover,
$D_{\alpha }\in M$
. Moreover,
![]() $A_{\alpha }\cup D_{\alpha }\in M$
is a pre-dense subset of
$A_{\alpha }\cup D_{\alpha }\in M$
is a pre-dense subset of
![]() $\mathbb {P}$
in M and thus,
$\mathbb {P}$
in M and thus,
![]() $g\cap (A_{\alpha }\cup D_{\alpha })\neq \emptyset $
by the M-genericity of g. Suppose for the sake of contradiction that
$g\cap (A_{\alpha }\cup D_{\alpha })\neq \emptyset $
by the M-genericity of g. Suppose for the sake of contradiction that
![]() $g\cap D_{\alpha }\neq \emptyset $
and let
$g\cap D_{\alpha }\neq \emptyset $
and let
![]() $q\in g\cap D_{\alpha }$
. Since
$q\in g\cap D_{\alpha }$
. Since
![]() $q,p\in g$
, there is
$q,p\in g$
, there is
![]() $r\in g$
such that
$r\in g$
such that
![]() $r\leq q,p$
. However, this means that
$r\leq q,p$
. However, this means that
![]() $r\in W_{\varphi ,\check {\alpha },\dot {y}}$
, since
$r\in W_{\varphi ,\check {\alpha },\dot {y}}$
, since
![]() $r\leq p$
. But r is incompatible with every element of
$r\leq p$
. But r is incompatible with every element of
![]() $A_{\alpha }$
, so
$A_{\alpha }$
, so
![]() $A_{\alpha }$
is not a maximal antichain in
$A_{\alpha }$
is not a maximal antichain in
![]() $W_{\varphi ,\check {\alpha },\dot {y}}$
. Contradiction! Thus,
$W_{\varphi ,\check {\alpha },\dot {y}}$
. Contradiction! Thus,
![]() $A_{\alpha }\cap g\neq \emptyset $
.
$A_{\alpha }\cap g\neq \emptyset $
.
We have established that for all
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $A_{\alpha }\cap g\neq \emptyset $
. Moreover, by Theorem 8, we have that
$A_{\alpha }\cap g\neq \emptyset $
. Moreover, by Theorem 8, we have that
This is the antecedence of an instance of the
![]() $\Delta _{0}$
-collection scheme since the part in parentheses is
$\Delta _{0}$
-collection scheme since the part in parentheses is
![]() $\Sigma _{1}$
(note that we are using here the fact that
$\Sigma _{1}$
(note that we are using here the fact that
![]() $\Vdash _{M}^{\mathbb {P}}$
for
$\Vdash _{M}^{\mathbb {P}}$
for
![]() $\Sigma _{1}$
statements is
$\Sigma _{1}$
statements is
![]() $\Sigma _{1}$
definable over M which is true by Theorem 8). Thus, there is
$\Sigma _{1}$
definable over M which is true by Theorem 8). Thus, there is
![]() $z\in M$
such that
$z\in M$
such that
Let
![]() $z^{g}:=\{\dot {x}^{g}:x\in z\cap M^{\mathbb {P}}\}$
. Note that
$z^{g}:=\{\dot {x}^{g}:x\in z\cap M^{\mathbb {P}}\}$
. Note that
![]() $z^{g}\in M[g]$
, as
$z^{g}\in M[g]$
, as
![]() $z\cap M^{\mathbb {P}}\in M\cap M^{\mathbb {P}}$
. It follows that
$z\cap M^{\mathbb {P}}\in M\cap M^{\mathbb {P}}$
. It follows that
a contradiction!
Let us now turn towards the second case, i.e., we assume that for all
![]() $\lambda <\delta $
there is
$\lambda <\delta $
there is
![]() $z\in M[g]$
such that
$z\in M[g]$
such that
Let us associate to
![]() $\psi $
a function
$\psi $
a function
![]() $f\in \Sigma _{1}^{M[g]}(M[g])$
such that
$f\in \Sigma _{1}^{M[g]}(M[g])$
such that
![]() $f:\delta \rightarrow \operatorname {\mathrm {OR}}^{M[g]}$
and for
$f:\delta \rightarrow \operatorname {\mathrm {OR}}^{M[g]}$
and for
![]() $\alpha <\delta $
,
$\alpha <\delta $
,
![]() $f(\alpha )$
is the least
$f(\alpha )$
is the least
![]() $\beta $
such that there is
$\beta $
such that there is
![]() $x\in M\vert \vert \beta [g]$
such that
$x\in M\vert \vert \beta [g]$
such that
![]() $M[g]\models \psi (\alpha ,x,y)$
. By our assumption
$M[g]\models \psi (\alpha ,x,y)$
. By our assumption
![]() $f\!\upharpoonright \!\alpha \in M[g]$
for every
$f\!\upharpoonright \!\alpha \in M[g]$
for every
![]() $\alpha <\delta $
, but
$\alpha <\delta $
, but
![]() $f\notin M[g]$
. Let us define an auxiliary function F with domain
$f\notin M[g]$
. Let us define an auxiliary function F with domain
![]() $\delta $
such that
$\delta $
such that
![]() $F(\alpha )=f\!\upharpoonright \!\alpha $
. Note that
$F(\alpha )=f\!\upharpoonright \!\alpha $
. Note that
![]() $F\in \Sigma _{1}^{M[g]}(M[g])$
. Let
$F\in \Sigma _{1}^{M[g]}(M[g])$
. Let
![]() $\varphi ^\prime _{F}$
be a
$\varphi ^\prime _{F}$
be a
![]() $\Sigma _1$
formula and
$\Sigma _1$
formula and
![]() $z\in M[g]$
such that
$z\in M[g]$
such that
and let
![]() $\varphi _F(a,b,z)$
be the formula
$\varphi _F(a,b,z)$
be the formula
Let
Note that
![]() $X\in \Sigma _{1}^{M}(M)$
and let
$X\in \Sigma _{1}^{M}(M)$
and let
![]() $\varphi _{X}$
be the defining formula and
$\varphi _{X}$
be the defining formula and
![]() $a\in M$
the corresponding parameter.
$a\in M$
the corresponding parameter.
We now aim to construct in a similar way as in the proof of Lemma 9 a maximal antichain A in X. If
![]() $X \neq \emptyset $
, let
$X \neq \emptyset $
, let
![]() $A_{0}:=\{p\}$
for some
$A_{0}:=\{p\}$
for some
![]() $p\in X$
. Otherwise, set
$p\in X$
. Otherwise, set
![]() $A_0 = \emptyset $
. Suppose that
$A_0 = \emptyset $
. Suppose that
![]() $\langle A_{i}:i<\gamma \rangle $
is defined via a
$\langle A_{i}:i<\gamma \rangle $
is defined via a
![]() $\Sigma _{1}$
-recursion for some
$\Sigma _{1}$
-recursion for some
![]() $\gamma <\operatorname {\mathrm {OR}}^{M}$
. If
$\gamma <\operatorname {\mathrm {OR}}^{M}$
. If
![]() $\gamma $
is a limit ordinal, let
$\gamma $
is a limit ordinal, let
![]() $A_{\gamma }=\bigcup _{i<\gamma }A_{i}$
. Then,
$A_{\gamma }=\bigcup _{i<\gamma }A_{i}$
. Then,
![]() $A_{\gamma }\in M$
and
$A_{\gamma }\in M$
and
![]() $\langle A_{i}:i\leq \gamma \rangle \in \Sigma _{1}^{M}(M)$
. If
$\langle A_{i}:i\leq \gamma \rangle \in \Sigma _{1}^{M}(M)$
. If
![]() $\gamma $
is not a limit, let
$\gamma $
is not a limit, let
![]() $\beta _{\gamma }<\operatorname {\mathrm {OR}}^{M}$
be the least
$\beta _{\gamma }<\operatorname {\mathrm {OR}}^{M}$
be the least
![]() $\beta $
such that
$\beta $
such that
if there exists such
![]() $\beta $
. In the case that there is no such
$\beta $
. In the case that there is no such
![]() $\beta $
, stop the recursion. In case
$\beta $
, stop the recursion. In case
![]() $\beta _{\gamma }$
is defined, let
$\beta _{\gamma }$
is defined, let
![]() $p_{\gamma }$
be the
$p_{\gamma }$
be the
![]() $<_{M}$
-least p such that
$<_{M}$
-least p such that
Let
![]() $A_{\gamma }:=A_{\gamma -1}\cup \{p_{\gamma }\}$
. It is not hard to verify that
$A_{\gamma }:=A_{\gamma -1}\cup \{p_{\gamma }\}$
. It is not hard to verify that
![]() $\langle A_{i}:i\leq \gamma \rangle \in \Sigma _{1}^{M}(M)$
and
$\langle A_{i}:i\leq \gamma \rangle \in \Sigma _{1}^{M}(M)$
and
![]() ${A_{\gamma }\in M}$
.
${A_{\gamma }\in M}$
.
Similar to the proof of the Lemma 9 we aim to see that there is a least
![]() $\gamma <\operatorname {\mathrm {OR}}^{M}$
such that
$\gamma <\operatorname {\mathrm {OR}}^{M}$
such that
![]() $\beta _{\gamma }$
is undefined, which will show that
$\beta _{\gamma }$
is undefined, which will show that
![]() $A:=A_{\gamma -1}$
is a maximal antichain in X and
$A:=A_{\gamma -1}$
is a maximal antichain in X and
![]() $A\in M$
.
$A\in M$
.
Suppose for the sake of contradiction that for all
![]() $\gamma <\operatorname {\mathrm {OR}}^{M}$
,
$\gamma <\operatorname {\mathrm {OR}}^{M}$
,
![]() $\beta _{\gamma }$
is defined. Let
$\beta _{\gamma }$
is defined. Let
![]() $\bar {A}:=\bigcup _{\gamma <\operatorname {\mathrm {OR}}^{M}}A_{\gamma }$
. Clearly,
$\bar {A}:=\bigcup _{\gamma <\operatorname {\mathrm {OR}}^{M}}A_{\gamma }$
. Clearly,
![]() $\bar {A}\in \Sigma _{1}^{M}(M)$
. Since
$\bar {A}\in \Sigma _{1}^{M}(M)$
. Since
![]() $\bar {A}$
is by construction an antichain, by Lemma 5
$\bar {A}$
is by construction an antichain, by Lemma 5
![]() $\bar {A}$
is bounded in
$\bar {A}$
is bounded in
![]() $\delta $
. In particular,
$\delta $
. In particular,
![]() $\bar {A}\in M$
. However, as in the previous proof, the definition of
$\bar {A}\in M$
. However, as in the previous proof, the definition of
![]() $\bar {A}$
give rise to a function
$\bar {A}$
give rise to a function
![]() $f\in \Sigma _{1}^{M}(M)$
such that
$f\in \Sigma _{1}^{M}(M)$
such that
![]() $\operatorname {\mathrm {dom}}(f)=\bar {A}$
and f is cofinal in
$\operatorname {\mathrm {dom}}(f)=\bar {A}$
and f is cofinal in
![]() $\operatorname {\mathrm {OR}}^{M}$
. But this is a contradiction!
$\operatorname {\mathrm {OR}}^{M}$
. But this is a contradiction!
Let
![]() $D:=\{p\in \mathbb {P}:\forall q\in A(q\perp p)\}$
. As
$D:=\{p\in \mathbb {P}:\forall q\in A(q\perp p)\}$
. As
![]() $A\in M$
,
$A\in M$
,
![]() $D\in M$
and thus,
$D\in M$
and thus,
![]() $A\cup D\in M$
.
$A\cup D\in M$
.
![]() $A\cup M$
is pre-dense and therefore,
$A\cup M$
is pre-dense and therefore,
![]() $g\cap (A\cup D)\neq \emptyset $
. Note that
$g\cap (A\cup D)\neq \emptyset $
. Note that
![]() $g\cap A=\emptyset $
, so
$g\cap A=\emptyset $
, so
![]() ${g\cap D\neq \emptyset} $
.
${g\cap D\neq \emptyset} $
.
Let
![]() $\tilde {p}\in D\cap g$
. Note that this means that there is no extension p of
$\tilde {p}\in D\cap g$
. Note that this means that there is no extension p of
![]() $\tilde {p}$
such that
$\tilde {p}$
such that
We claim that there is
![]() $\vec {p} = \langle p_{i}:i<\delta \rangle \in M$
such that for all
$\vec {p} = \langle p_{i}:i<\delta \rangle \in M$
such that for all
![]() $i < \delta $
,
$i < \delta $
,
![]() $p_i \leq \tilde {p}$
and
$p_i \leq \tilde {p}$
and
![]() $M \models \psi (i,\dot {z},p_i)$
, where
$M \models \psi (i,\dot {z},p_i)$
, where
![]() $\psi (i,\dot {z},p)$
is the statement
$\psi (i,\dot {z},p)$
is the statement
We may find such
![]() $\langle p_{i}:i<\delta \rangle $
in M, as
$\langle p_{i}:i<\delta \rangle $
in M, as
![]() $\Delta _{0}$
-collection holds in M and
$\Delta _{0}$
-collection holds in M and
For every
![]() $i<\delta $
there exists such
$i<\delta $
there exists such
![]() $p\in \mathbb {P}$
, since
$p\in \mathbb {P}$
, since
![]() $\tilde {p}\in g$
and
$\tilde {p}\in g$
and
![]() $M[g]\models \forall i<\delta \exists y\varphi _{F}(i,y,z)$
and so by Theorem 8 the existence of p follows.
$M[g]\models \forall i<\delta \exists y\varphi _{F}(i,y,z)$
and so by Theorem 8 the existence of p follows.
Claim 2. There is
![]() $i_0 <\delta $
such that for all
$i_0 <\delta $
such that for all
![]() $i \in [i_0,\delta )$
and all
$i \in [i_0,\delta )$
and all
![]() $q\in \mathbb {P}$
with
$q\in \mathbb {P}$
with
![]() $q\leq p_i$
and for all
$q\leq p_i$
and for all
![]() $j \in (i,\delta )$
, there is
$j \in (i,\delta )$
, there is
![]() $k\in [j,\delta )$
such that
$k\in [j,\delta )$
such that
![]() $q \mid \mid p_k$
.
$q \mid \mid p_k$
.
Proof. This follows routinely from the
![]() $\delta $
-c.c. of
$\delta $
-c.c. of
![]() $\mathbb {P}$
in M (otherwise, working in M, construct by recursion on
$\mathbb {P}$
in M (otherwise, working in M, construct by recursion on
![]() $\beta $
an antichain
$\beta $
an antichain
![]() $\langle q_i \rangle _{i<\delta }$
).
$\langle q_i \rangle _{i<\delta }$
).
Now since
![]() $p_{i_0}\leq \tilde {p}$
, the following claim gives a contradiction, completing the proof:
$p_{i_0}\leq \tilde {p}$
, the following claim gives a contradiction, completing the proof:
Claim 3. Replacing p with
![]() $p_{i_0}$
, line (2.2) holds.
$p_{i_0}$
, line (2.2) holds.
Proof. Let h be
![]() $(M,\mathbb {P})$
-generic with
$(M,\mathbb {P})$
-generic with
![]() $p_{i_0} \in h$
. By Claim 2, for every
$p_{i_0} \in h$
. By Claim 2, for every
![]() $\beta \in (i_0,\delta )$
,
$\beta \in (i_0,\delta )$
,
![]() $h \cap \{ p_j \mid j \in (i, \delta ) \} \neq \emptyset $
. So there are cofinally many
$h \cap \{ p_j \mid j \in (i, \delta ) \} \neq \emptyset $
. So there are cofinally many
![]() $i < \delta $
such that
$i < \delta $
such that
![]() $p_i \in h$
. By KP in M, we can fix
$p_i \in h$
. By KP in M, we can fix
![]() $\xi <\operatorname {\mathrm {OR}}^M$
such that
$\xi <\operatorname {\mathrm {OR}}^M$
such that
![]() $M \vert \xi $
satisfies
$M \vert \xi $
satisfies
![]() $\psi (i,\dot {z},p_i)$
for all
$\psi (i,\dot {z},p_i)$
for all
![]() $i<\delta $
. Therefore,
$i<\delta $
. Therefore,
![]() $M \vert \vert \xi [h]$
satisfies
$M \vert \vert \xi [h]$
satisfies
![]() $\exists y \varphi _F (i,y,z)$
for cofinally many
$\exists y \varphi _F (i,y,z)$
for cofinally many
![]() $i < \delta $
. Note that for all
$i < \delta $
. Note that for all
![]() $j_0<j_1<\delta $
and all
$j_0<j_1<\delta $
and all
![]() $p\in \mathbb {P}$
, if
$p\in \mathbb {P}$
, if
![]() $M \vert \xi $
satisfies
$M \vert \xi $
satisfies
![]() $\psi (j_1,\dot {z},p)$
then
$\psi (j_1,\dot {z},p)$
then
![]() $M \vert \xi $
satisfies
$M \vert \xi $
satisfies
![]() $\psi (j_0,\dot {z},p)$
.Footnote
6
Thus,
$\psi (j_0,\dot {z},p)$
.Footnote
6
Thus,
![]() $M \vert \vert \xi [h]$
satisfies
$M \vert \vert \xi [h]$
satisfies
![]() $\exists y \varphi _F(i,y,z)$
for all
$\exists y \varphi _F(i,y,z)$
for all
![]() $i < \delta $
.
$i < \delta $
.
As stated prior the claim, this completes the proof.
From Theorem 10 we immediately get the following corollary.
Corollary 11. Suppose that M is an admissible passive premouse with a largest, regular, and uncountable cardinal
![]() $\delta $
which is Woodin in M and let
$\delta $
which is Woodin in M and let
![]() $\mathbb {B}\in M$
be the extender algebra with
$\mathbb {B}\in M$
be the extender algebra with
![]() $\delta $
-many generators as defined inside M. Let
$\delta $
-many generators as defined inside M. Let
![]() $g\subset \mathbb {B}$
be M-generic. Then
$g\subset \mathbb {B}$
be M-generic. Then
![]() $M[g]\models \text {KP}$
.
$M[g]\models \text {KP}$
.
If we replaced
![]() $M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}$
” in the statement of Theorem 10 with
$M\models "\mathbb {P}\text { has the }\delta \text {-c.c.}$
” in the statement of Theorem 10 with
![]() ${M\models "\mathbb {P}\text { is }<\delta \text {-closed,}"}$
Theorem 10 is false as Proposition 13 shows.
${M\models "\mathbb {P}\text { is }<\delta \text {-closed,}"}$
Theorem 10 is false as Proposition 13 shows.
Lemma 12. Suppose that M,
![]() $M_{1}$
, and
$M_{1}$
, and
![]() $M_{2}$
are sound premice such that
$M_{2}$
are sound premice such that
![]() $\operatorname {\mathrm {OR}}^{M}$
is a regular, uncountable cardinal (in V),
$\operatorname {\mathrm {OR}}^{M}$
is a regular, uncountable cardinal (in V),
![]() $\rho _{\omega }^{M_{1}}=\rho _{\omega }^{M_{2}}=\operatorname {\mathrm {OR}}^{M}$
,
$\rho _{\omega }^{M_{1}}=\rho _{\omega }^{M_{2}}=\operatorname {\mathrm {OR}}^{M}$
,
![]() $M \unlhd M_1$
,
$M \unlhd M_1$
,
![]() $M \unlhd M_2$
, and Condensation holds of
$M \unlhd M_2$
, and Condensation holds of
![]() $M_{1}$
and
$M_{1}$
and
![]() $M_{2}$
. Then, either
$M_{2}$
. Then, either
![]() $M_{1}\unlhd M_{2}$
or
$M_{1}\unlhd M_{2}$
or
![]() $M_{2}\unlhd M_{1}$
.
$M_{2}\unlhd M_{1}$
.
The Lemma follows from the proof of Lemma 3.1 in [Reference Jensen, Schimmerling, Schindler and Steel4].
Let
![]() $M = L_{\omega _1^{\operatorname {\mathrm {CK}}}}$
and
$M = L_{\omega _1^{\operatorname {\mathrm {CK}}}}$
and
![]() $\mathbb {P}$
be Cohen forcing. By [Reference Greenberg and Monin2], there are
$\mathbb {P}$
be Cohen forcing. By [Reference Greenberg and Monin2], there are
![]() $(M,\mathbb {P})$
-generics g such that
$(M,\mathbb {P})$
-generics g such that
![]() $M[g] \not \models \text {KP}$
.Footnote
7
The following proposition establishes a variant of this fact.
$M[g] \not \models \text {KP}$
.Footnote
7
The following proposition establishes a variant of this fact.
Proposition 13. Let
![]() $M = (\lfloor M \rfloor , \in , \mathbb {E}^M, \emptyset )$
be a
$M = (\lfloor M \rfloor , \in , \mathbb {E}^M, \emptyset )$
be a
![]() $1$
-sound admissible passive premouse with a largest, regular cardinal
$1$
-sound admissible passive premouse with a largest, regular cardinal
![]() $\delta $
such that
$\delta $
such that
![]() $\rho _{1}^{M}<\operatorname {\mathrm {OR}}^{M}$
and suppose that Condensation holds in M. Let
$\rho _{1}^{M}<\operatorname {\mathrm {OR}}^{M}$
and suppose that Condensation holds in M. Let
![]() $\mathbb {C}_{\delta }:=(\delta ^{<\delta })^{M}$
. Then there is an M-generic
$\mathbb {C}_{\delta }:=(\delta ^{<\delta })^{M}$
. Then there is an M-generic
![]() $g\subset \mathbb {C}_{\delta }$
such that
$g\subset \mathbb {C}_{\delta }$
such that
![]() $(\lfloor M[g] \rfloor , \in ) \not \models \text {KP}$
.
$(\lfloor M[g] \rfloor , \in ) \not \models \text {KP}$
.
Proof. Note that
![]() $\mathbb {\mathbb {C}_{\delta }}\in M$
is such that
$\mathbb {\mathbb {C}_{\delta }}\in M$
is such that
By Lemma 4 and
![]() $1$
-soundness,
$1$
-soundness,
![]() $\delta =\rho _{1}^{M}$
and
$\delta =\rho _{1}^{M}$
and
![]() $M=H_{1}^{M}(\delta \cup \{p_{1}^{M}\})$
. Thus, there is a partial surjective function
$M=H_{1}^{M}(\delta \cup \{p_{1}^{M}\})$
. Thus, there is a partial surjective function
![]() $h:\delta \rightarrow M$
such that
$h:\delta \rightarrow M$
such that
![]() $h\in \Sigma _{1}^{M}(\{p_{1}^{M}\})$
. Let
$h\in \Sigma _{1}^{M}(\{p_{1}^{M}\})$
. Let
Note that
![]() $\tilde {D}\notin M$
, as otherwise M could construct an M-generic. Let
$\tilde {D}\notin M$
, as otherwise M could construct an M-generic. Let
be the monotone enumeration of
![]() $\tilde {D}$
. Note that
$\tilde {D}$
. Note that
![]() $\tilde {D}$
has ordertype
$\tilde {D}$
has ordertype
![]() $\delta $
. Since
$\delta $
. Since
![]() $h\in \Sigma _{1}^{M}(M)$
,
$h\in \Sigma _{1}^{M}(M)$
,
![]() $\tilde {D}\in \Sigma _{1}^{M}(M)$
. However,
$\tilde {D}\in \Sigma _{1}^{M}(M)$
. However,
![]() $D\notin \Sigma _{1}^{M}(M)$
, as otherwise by
$D\notin \Sigma _{1}^{M}(M)$
, as otherwise by
![]() $\Delta _{0}$
-collection,
$\Delta _{0}$
-collection,
![]() $D\in M$
.
$D\in M$
.
The idea is now to construct an M-generic g which codes in a
![]() $\Sigma _{1}$
-fashion the set D so that
$\Sigma _{1}$
-fashion the set D so that
![]() $D\in M[g]$
if
$D\in M[g]$
if
![]() $(\lfloor M[g] \rfloor , \in ) \models \text {KP}$
.
$(\lfloor M[g] \rfloor , \in ) \models \text {KP}$
.
Let us define
![]() $\tilde {g} = \langle p_{i}:i<\delta \rangle $
via a recursion on i such that for all
$\tilde {g} = \langle p_{i}:i<\delta \rangle $
via a recursion on i such that for all
![]() $\alpha < \delta $
,
$\alpha < \delta $
,
![]() $\langle p_{i}:i<\alpha \rangle $
is uniformly
$\langle p_{i}:i<\alpha \rangle $
is uniformly
![]() $\Sigma _1$
over M in the parameters
$\Sigma _1$
over M in the parameters
![]() $\{D\!\upharpoonright \! \alpha , \mathbb {C}_\delta \}$
. We will have that
$\{D\!\upharpoonright \! \alpha , \mathbb {C}_\delta \}$
. We will have that
![]() $p_{i}\leq p_{j}$
for
$p_{i}\leq p_{j}$
for
![]() $j<i$
. Set
$j<i$
. Set
![]() $p_{0}:=\langle \xi _{0}\rangle $
and
$p_{0}:=\langle \xi _{0}\rangle $
and
![]() $p_{1}$
to be the
$p_{1}$
to be the
![]() $<_{M}$
-least
$<_{M}$
-least
![]() $p\in h(\xi _{0})$
such that
$p\in h(\xi _{0})$
such that
![]() $p\leq p_{0}$
. Note that there is such p, since
$p\leq p_{0}$
. Note that there is such p, since
![]() $h(\xi _{0})$
is dense in
$h(\xi _{0})$
is dense in
![]() $\mathbb {C}_{\delta }$
.
$\mathbb {C}_{\delta }$
.
Suppose that
![]() $\langle p_{i}:i<\lambda \rangle $
is defined, where
$\langle p_{i}:i<\lambda \rangle $
is defined, where
![]() $\lambda <\delta $
is a limit ordinal, such that
$\lambda <\delta $
is a limit ordinal, such that
![]() $p_{i}\leq p_{j}$
for
$p_{i}\leq p_{j}$
for
![]() $j\leq i<\lambda $
. Note that
$j\leq i<\lambda $
. Note that
![]() $D\!\upharpoonright \!\lambda \in M$
, since
$D\!\upharpoonright \!\lambda \in M$
, since
![]() $\tilde {D}\in \Sigma _{1}^{M}(M)$
and
$\tilde {D}\in \Sigma _{1}^{M}(M)$
and
![]() $\delta $
is
$\delta $
is
![]() $\Sigma _{1}^M (M)$
-regular by Lemma 6. By our induction hypothesis the construction so far is uniformly
$\Sigma _{1}^M (M)$
-regular by Lemma 6. By our induction hypothesis the construction so far is uniformly
![]() $\Sigma _{1}$
in the parameters
$\Sigma _{1}$
in the parameters
![]() $D\!\upharpoonright \!\lambda $
and
$D\!\upharpoonright \!\lambda $
and
![]() $\mathbb {C}_{\delta }$
. This implies that
$\mathbb {C}_{\delta }$
. This implies that
![]() $\langle p_{i}:i<\lambda \rangle \in M$
. Thus, we can set
$\langle p_{i}:i<\lambda \rangle \in M$
. Thus, we can set
![]() $p_{\lambda }=(\bigcup _{i<\lambda }p_{i})^{\frown }\langle \xi _{\lambda }\rangle $
. Let
$p_{\lambda }=(\bigcup _{i<\lambda }p_{i})^{\frown }\langle \xi _{\lambda }\rangle $
. Let
![]() $p_{\lambda +1}$
be the
$p_{\lambda +1}$
be the
![]() $<_{M}$
-least
$<_{M}$
-least
![]() $p\in h(\xi _{\lambda })$
such that
$p\in h(\xi _{\lambda })$
such that
![]() $p\leq p_{\lambda }$
.
$p\leq p_{\lambda }$
.
We now turn towards the successor case. Suppose we have defined
![]() $\langle p_\beta \rangle _{\beta \leq \gamma }$
where
$\langle p_\beta \rangle _{\beta \leq \gamma }$
where
![]() $\gamma $
is an odd successor (that is,
$\gamma $
is an odd successor (that is,
![]() $\gamma =\lambda +2n+1$
for some
$\gamma =\lambda +2n+1$
for some
![]() $n<\omega $
and
$n<\omega $
and
![]() $\lambda $
is a limit less than
$\lambda $
is a limit less than
![]() $\gamma $
or equal to
$\gamma $
or equal to
![]() $0$
). Set
$0$
). Set
![]() $p_{\gamma + 1} := p_{\gamma }^{\frown }\langle \xi _{\lambda +n}\rangle $
and let
$p_{\gamma + 1} := p_{\gamma }^{\frown }\langle \xi _{\lambda +n}\rangle $
and let
![]() $p_{\gamma + 2}$
be the
$p_{\gamma + 2}$
be the
![]() $<_{M}$
-least
$<_{M}$
-least
![]() $p\in h(\xi _{\lambda +n})$
such that
$p\in h(\xi _{\lambda +n})$
such that
![]() $p\leq p_{\gamma +1}$
.
$p\leq p_{\gamma +1}$
.
Let g be the upwards-closure of
![]() $\tilde {g}$
in
$\tilde {g}$
in
![]() $\mathbb {\mathbb {C}_{\delta }}$
. By definition of
$\mathbb {\mathbb {C}_{\delta }}$
. By definition of
![]() $\tilde {g}$
, g is M-generic. Note that since
$\tilde {g}$
, g is M-generic. Note that since
![]() $\mathbb {E}^{M}\!\upharpoonright \!\delta \in M[g]$
by Lemma 12 we can define
$\mathbb {E}^{M}\!\upharpoonright \!\delta \in M[g]$
by Lemma 12 we can define
![]() $\mathbb {E}^{M}$
over
$\mathbb {E}^{M}$
over
![]() $M[g]$
in a
$M[g]$
in a
![]() $\Sigma _{1}$
fashion as the extender sequence of the stack of sound premice extending
$\Sigma _{1}$
fashion as the extender sequence of the stack of sound premice extending
![]() $M\vert \delta $
which project to
$M\vert \delta $
which project to
![]() $\delta $
and for which condensation holds. Thus, it follows that
$\delta $
and for which condensation holds. Thus, it follows that
![]() ${(M, \in , \mathbb {E}^M) \in \Sigma _{1}^{(\lfloor M[g] \rfloor , \in )}(\{ M \vert \delta \})}$
. Note that therefore
${(M, \in , \mathbb {E}^M) \in \Sigma _{1}^{(\lfloor M[g] \rfloor , \in )}(\{ M \vert \delta \})}$
. Note that therefore
![]() $\tilde {g}$
is definable over
$\tilde {g}$
is definable over
![]() $(M[g], \in )$
from
$(M[g], \in )$
from
![]() $\{\mathbb {C}_{\delta },\delta ,g, M \vert \delta \}$
via a
$\{\mathbb {C}_{\delta },\delta ,g, M \vert \delta \}$
via a
![]() $\Sigma _{1}$
recursion of length
$\Sigma _{1}$
recursion of length
![]() $\delta $
. Thus, if
$\delta $
. Thus, if
![]() $(\lfloor M[g] \rfloor , \in ) \models \text {KP}$
, then
$(\lfloor M[g] \rfloor , \in ) \models \text {KP}$
, then
![]() $\tilde {g} \in M[g]$
and so
$\tilde {g} \in M[g]$
and so
![]() $D \in M[g]$
.
$D \in M[g]$
.
Let
![]() $h^{\prime }:\delta \rightarrow \operatorname {\mathrm {OR}}^{M}$
be the partial function such that
$h^{\prime }:\delta \rightarrow \operatorname {\mathrm {OR}}^{M}$
be the partial function such that
![]() $h^{\prime }(\alpha )$
is the least
$h^{\prime }(\alpha )$
is the least
![]() ${\beta <\operatorname {\mathrm {OR}}^{M}}$
such that
${\beta <\operatorname {\mathrm {OR}}^{M}}$
such that
![]() $h(\alpha )\in M \vert \beta $
, if
$h(\alpha )\in M \vert \beta $
, if
![]() $h(\alpha )$
is defined. Clearly,
$h(\alpha )$
is defined. Clearly,
![]() $h^{\prime }\in \Sigma _{1}^{M}(\{p_{1}^{M}\})$
. We have that
$h^{\prime }\in \Sigma _{1}^{M}(\{p_{1}^{M}\})$
. We have that
![]() $h^{\prime }\in \Sigma _{1}^{(\lfloor M[g] \rfloor , \in )}(\lfloor M[g] \rfloor )$
. Moreover, as
$h^{\prime }\in \Sigma _{1}^{(\lfloor M[g] \rfloor , \in )}(\lfloor M[g] \rfloor )$
. Moreover, as
![]() $\mathbb {C}_{\delta }$
is
$\mathbb {C}_{\delta }$
is
![]() $<\delta $
-closed and atom-less,
$<\delta $
-closed and atom-less,
![]() ${\operatorname {\mathrm {ran}}(h^{\prime }\!\upharpoonright \! D)}$
is cofinal in M. Since
${\operatorname {\mathrm {ran}}(h^{\prime }\!\upharpoonright \! D)}$
is cofinal in M. Since
![]() $\operatorname {\mathrm {OR}}^{M}=\operatorname {\mathrm {OR}}^{M[g]}$
,
$\operatorname {\mathrm {OR}}^{M}=\operatorname {\mathrm {OR}}^{M[g]}$
,
![]() $h^\prime \!\upharpoonright \! D$
is cofinal in
$h^\prime \!\upharpoonright \! D$
is cofinal in
![]() $M[g]$
. But now if
$M[g]$
. But now if
![]() $(\lfloor M[g] \rfloor , \,{\in}) \models \text {KP,}$
since
$(\lfloor M[g] \rfloor , \,{\in}) \models \text {KP,}$
since
![]() $D\in M[g]$
,
$D\in M[g]$
,
![]() $\operatorname {\mathrm {OR}}^{M[g]}\in M[g]$
. Contradiction! Thus,
$\operatorname {\mathrm {OR}}^{M[g]}\in M[g]$
. Contradiction! Thus,
![]() ${(\lfloor M[g] \rfloor , \in ) \not \models \text {KP}}$
.
${(\lfloor M[g] \rfloor , \in ) \not \models \text {KP}}$
.
2.2 Preservation of admissibility between iterates of premice
Next we deal with the preservation of admissibility between iterates of premice. Parts of this will be used in the proof of Lemma 25.
Lemma 14. Suppose that M and N are premice and let
![]() $i:M\rightarrow N$
be
$i:M\rightarrow N$
be
![]() $r\Sigma _{3}$
-elementary. Then
$r\Sigma _{3}$
-elementary. Then
![]() $M\models \text {KP}$
iff
$M\models \text {KP}$
iff
![]() $N\models \text {KP}$
.
$N\models \text {KP}$
.
The lemma follows directly from the fact that the part of KP excluding the induction axioms has an
![]() $r\Pi _{3}$
axiomatization and is therefore preserved under
$r\Pi _{3}$
axiomatization and is therefore preserved under
![]() $r\Sigma _{3}$
-elementary embeddings between premice.
$r\Sigma _{3}$
-elementary embeddings between premice.
Thus, by Lemma 14, if
![]() $\text {Ult}_{n}(M,E)$
is wellfounded,
$\text {Ult}_{n}(M,E)$
is wellfounded,
![]() $\text {Ult}_{n}(M,E) \models \text {KP}$
if
$\text {Ult}_{n}(M,E) \models \text {KP}$
if
![]() $n\geq 2$
and M is an admissible passive premouse.
$n\geq 2$
and M is an admissible passive premouse.
Lemma 15. Let
![]() $k\leq \omega $
and let N be a k-sound premouse. Let
$k\leq \omega $
and let N be a k-sound premouse. Let
![]() $\mathcal {T}$
be a k-maximal iteration tree on N such that
$\mathcal {T}$
be a k-maximal iteration tree on N such that
![]() $\operatorname {\mathrm {lh}}(\mathcal {T})=\theta +1$
. Let
$\operatorname {\mathrm {lh}}(\mathcal {T})=\theta +1$
. Let
![]() $b:=[0,\theta ]^{\mathcal {T}}$
be the main branch of
$b:=[0,\theta ]^{\mathcal {T}}$
be the main branch of
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\alpha $
be least such that
$\alpha $
be least such that
![]() $\alpha + 1 \in b$
and
$\alpha + 1 \in b$
and
![]() $(\alpha +1,\theta ]^{\mathcal {T}}$
does not drop in model. Let
$(\alpha +1,\theta ]^{\mathcal {T}}$
does not drop in model. Let
![]() $\eta = \alpha +1$
. Then
$\eta = \alpha +1$
. Then
![]() $\mathcal {M}_{\eta }^{*\mathcal {T}}$
is an admissible passive premouse with a largest, regular, and uncountable cardinal if and only if
$\mathcal {M}_{\eta }^{*\mathcal {T}}$
is an admissible passive premouse with a largest, regular, and uncountable cardinal if and only if
![]() $\mathcal {M}_{\theta }^{\mathcal {T}}$
is an admissible passive premouse with a largest, regular, and uncountable cardinal.
$\mathcal {M}_{\theta }^{\mathcal {T}}$
is an admissible passive premouse with a largest, regular, and uncountable cardinal.
Proof. We prove the two directions separately.
Claim 1. Suppose
![]() $\mathcal {M}_{\eta }^{*\mathcal {T}}$
is an admissible passive premouse with a largest, regular, and uncountable cardinal. Then so is
$\mathcal {M}_{\eta }^{*\mathcal {T}}$
is an admissible passive premouse with a largest, regular, and uncountable cardinal. Then so is
![]() $\mathcal {M}_{\theta }^{\mathcal {T}}$
.
$\mathcal {M}_{\theta }^{\mathcal {T}}$
.
Proof. Note that in the case that
![]() $\deg ^{\mathcal {T}}(\theta )\geq 2$
, the lemma holds by Lemma 14. Thus, we may assume that
$\deg ^{\mathcal {T}}(\theta )\geq 2$
, the lemma holds by Lemma 14. Thus, we may assume that
![]() $\deg ^{\mathcal {T}}(\theta ) \leq 1$
.
$\deg ^{\mathcal {T}}(\theta ) \leq 1$
.
By standard facts
![]() $\mathcal {M}_{\theta }^{\mathcal {T}}$
is a passive premouse with a largest, regular, and uncountable cardinal. We have to verify that
$\mathcal {M}_{\theta }^{\mathcal {T}}$
is a passive premouse with a largest, regular, and uncountable cardinal. We have to verify that
![]() $\mathcal {M}_{\theta }^{\mathcal {T}}$
is admissible. By Lemma 3, it suffices to show that
$\mathcal {M}_{\theta }^{\mathcal {T}}$
is admissible. By Lemma 3, it suffices to show that
![]() $\Delta _{0}$
-collection holds in
$\Delta _{0}$
-collection holds in
![]() $\mathcal {M}_{\theta }^{\mathcal {T}}$
.
$\mathcal {M}_{\theta }^{\mathcal {T}}$
.
Case 1.
 $\theta = \zeta + 1$
is a successor ordinal.
$\theta = \zeta + 1$
is a successor ordinal.
We inductively assume that
![]() $\mathcal {M}^{*\mathcal {T}}_{\theta }$
is an admissible passive premouse with a largest, regular, and uncountable cardinal.
$\mathcal {M}^{*\mathcal {T}}_{\theta }$
is an admissible passive premouse with a largest, regular, and uncountable cardinal.
Let
![]() $n := \deg ^{\mathcal {T}} (\theta )$
,
$n := \deg ^{\mathcal {T}} (\theta )$
,
![]() $M:= \mathcal {M}^{*\mathcal {T}}_\theta $
,
$M:= \mathcal {M}^{*\mathcal {T}}_\theta $
,
![]() $E:=E_{\zeta }^{\mathcal {T}}$
, and
$E:=E_{\zeta }^{\mathcal {T}}$
, and
![]() $M^\prime := \text {Ult}_{n}(\mathcal {M}_\theta ^{*\mathcal {T}},E)$
. By our initial remarks
$M^\prime := \text {Ult}_{n}(\mathcal {M}_\theta ^{*\mathcal {T}},E)$
. By our initial remarks
![]() $n \leq 1$
. By standard arguments
$n \leq 1$
. By standard arguments
![]() $\kappa := \operatorname {\mathrm {crit}}(E)$
is strictly less than the largest cardinal of M. In particular, by Lemma 4,
$\kappa := \operatorname {\mathrm {crit}}(E)$
is strictly less than the largest cardinal of M. In particular, by Lemma 4,
![]() $\kappa < \rho _1^M$
.
$\kappa < \rho _1^M$
.
Since M is admissible we have by
![]() $\Delta _{0}$
-collection that for any
$\Delta _{0}$
-collection that for any
![]() $m<\omega $
,
$m<\omega $
,
![]() $f\in \Sigma _{1}^{M}(M)\cap {^{[\kappa ]^{m}}M}$
implies that
$f\in \Sigma _{1}^{M}(M)\cap {^{[\kappa ]^{m}}M}$
implies that
![]() $f\in M$
. This means that the canonical factor map
$f\in M$
. This means that the canonical factor map
![]() $\pi \colon \text {Ult}_{0}(M,E) \to \text {Ult}_{1}(M,E)$
is the identity. Thus,
$\pi \colon \text {Ult}_{0}(M,E) \to \text {Ult}_{1}(M,E)$
is the identity. Thus,
![]() $\text {Ult}_{0}(M,E)=\text {Ult}_{1}(M,E)$
and the associated ultrapower maps are the same. In particular,
$\text {Ult}_{0}(M,E)=\text {Ult}_{1}(M,E)$
and the associated ultrapower maps are the same. In particular,
![]() $i^{*\mathcal {T}}_{\theta }\colon M\to M^{\prime }$
is a
$i^{*\mathcal {T}}_{\theta }\colon M\to M^{\prime }$
is a
![]() $1$
-embedding and
$1$
-embedding and
![]() $i^{*\mathcal {T}}_{\theta }$
is cofinal in
$i^{*\mathcal {T}}_{\theta }$
is cofinal in
![]() $\operatorname {\mathrm {OR}}^{M^{\prime }}$
.
$\operatorname {\mathrm {OR}}^{M^{\prime }}$
.
Subclaim 1. For
![]() $a \in [\operatorname {\mathrm {lh}}(E)]^{<\omega }$
,
$a \in [\operatorname {\mathrm {lh}}(E)]^{<\omega }$
,
![]() $\text {Ult}_{0}(M,E_a) \models \text {KP}$
.
$\text {Ult}_{0}(M,E_a) \models \text {KP}$
.
Proof. Let
![]() $a \in [\operatorname {\mathrm {lh}}(E)]^{<\omega }$
and suppose for contradiction that
$a \in [\operatorname {\mathrm {lh}}(E)]^{<\omega }$
and suppose for contradiction that
![]() ${\text {Ult}_{0}(M,E_a) \not \models \text {KP}}$
. By our initial remarks this means that
${\text {Ult}_{0}(M,E_a) \not \models \text {KP}}$
. By our initial remarks this means that
![]() $\Delta _{0}$
-collection fails in
$\Delta _{0}$
-collection fails in
![]() $\text {Ult}_{0}(M,E_a)$
, i.e., there is a
$\text {Ult}_{0}(M,E_a)$
, i.e., there is a
![]() $\Sigma _{0}$
-formula
$\Sigma _{0}$
-formula
![]() $\varphi $
,
$\varphi $
,
![]() $\xi < \operatorname {\mathrm {OR}}^{\text {Ult}_{0}(M,E_a)}$
, and
$\xi < \operatorname {\mathrm {OR}}^{\text {Ult}_{0}(M,E_a)}$
, and
![]() $p\in \text {Ult}_{0}(M,E_a)$
such that
$p\in \text {Ult}_{0}(M,E_a)$
such that
but there is no
![]() $z\in \text {Ult}_{0}(M,E_a)$
such that
$z\in \text {Ult}_{0}(M,E_a)$
such that
Let
![]() $i \colon M \to \text {Ult}_{0}(M,E_a)$
be the ultrapower embedding. By our previous remarks we have that i is a
$i \colon M \to \text {Ult}_{0}(M,E_a)$
be the ultrapower embedding. By our previous remarks we have that i is a
![]() $1$
-embedding and cofinal in
$1$
-embedding and cofinal in
![]() $\operatorname {\mathrm {OR}}^{\text {Ult}_{0}(M,E_a)}$
.
$\operatorname {\mathrm {OR}}^{\text {Ult}_{0}(M,E_a)}$
.
Let
![]() $\delta $
be the largest cardinal of M and
$\delta $
be the largest cardinal of M and
![]() $\delta ^{\prime }=i(\delta )$
be the largest cardinal of
$\delta ^{\prime }=i(\delta )$
be the largest cardinal of
![]() $\text {Ult}_{0}(M,E_a)$
. By Lemma 3 we may assume that
$\text {Ult}_{0}(M,E_a)$
. By Lemma 3 we may assume that
![]() $\xi $
in (2.4) is equal to
$\xi $
in (2.4) is equal to
![]() $\delta ^{\prime }$
. Let
$\delta ^{\prime }$
. Let
![]() $j=\lvert a\rvert $
. Let
$j=\lvert a\rvert $
. Let
![]() $g^{\prime }\colon \delta ^\prime \to \text {Ult}_{0}(M,E_a)$
be the canonical function derived from
$g^{\prime }\colon \delta ^\prime \to \text {Ult}_{0}(M,E_a)$
be the canonical function derived from
![]() $\varphi $
by taking the
$\varphi $
by taking the
![]() $<_{\text {Ult}_{0}(M,E_a)}$
-least witness. Note that
$<_{\text {Ult}_{0}(M,E_a)}$
-least witness. Note that
![]() $g^{\prime }\in \Sigma _{1}^{\text {Ult}_{0}(M,E_a)}(\{p\})$
as
$g^{\prime }\in \Sigma _{1}^{\text {Ult}_{0}(M,E_a)}(\{p\})$
as
![]() $\varphi $
is
$\varphi $
is
![]() $\Sigma _{0}$
. We will now show that
$\Sigma _{0}$
. We will now show that
![]() $g^\prime $
is bounded in
$g^\prime $
is bounded in
![]() $\text {Ult}_{0}(M,E_a)$
. This will contradict the failure of
$\text {Ult}_{0}(M,E_a)$
. This will contradict the failure of
![]() $\Delta _0$
-collection, completing the proof.
$\Delta _0$
-collection, completing the proof.
By the definition of
![]() $\text {Ult}_{0}(M,E_a)$
we have for
$\text {Ult}_{0}(M,E_a)$
we have for
![]() $\alpha <\delta ^{\prime }$
some
$\alpha <\delta ^{\prime }$
some
![]() $f_{\!\alpha } \in {^{[\kappa ]^{j}}}\delta \cap M$
such that
$f_{\!\alpha } \in {^{[\kappa ]^{j}}}\delta \cap M$
such that
![]() $\alpha =[a,f_{\!\alpha }]_{E_a}^{M}$
. Also, there is
$\alpha =[a,f_{\!\alpha }]_{E_a}^{M}$
. Also, there is
![]() $f_{\!\!p}\in ({^{[\kappa ]^{j}}}M) \cap M$
such that
$f_{\!\!p}\in ({^{[\kappa ]^{j}}}M) \cap M$
such that
![]() $p=[a,f_{\!\!p}]_{E}^{M}$
. Since we assumed that
$p=[a,f_{\!\!p}]_{E}^{M}$
. Since we assumed that
![]() $\delta $
is regular in M and
$\delta $
is regular in M and
![]() $\kappa < \delta $
we may assume that for
$\kappa < \delta $
we may assume that for
![]() $\alpha <\delta ^\prime $
,
$\alpha <\delta ^\prime $
,
![]() $f_{\!\alpha }\in {^{[\kappa ]^{j}}}\delta \cap (M\vert \delta )$
. Moreover, since Łoś’s Theorem holds for
$f_{\!\alpha }\in {^{[\kappa ]^{j}}}\delta \cap (M\vert \delta )$
. Moreover, since Łoś’s Theorem holds for
![]() $\Sigma _{1}$
-formulae, we have by (2.4) for all
$\Sigma _{1}$
-formulae, we have by (2.4) for all
![]() $\alpha <\delta ^{\prime }$
,
$\alpha <\delta ^{\prime }$
,
Note that for any
![]() $h\in {^{[\kappa ]^{j}}} \delta \cap (M\vert \delta )$
there is some
$h\in {^{[\kappa ]^{j}}} \delta \cap (M\vert \delta )$
there is some
![]() $\alpha <\delta ^{\prime }$
such that
$\alpha <\delta ^{\prime }$
such that
![]() $\alpha =[a,h]_{E}^{M}$
. Thus,
$\alpha =[a,h]_{E}^{M}$
. Thus,
Note that this does make sense since
![]() $E_a \in M$
: By standard facts about k-maximal iteration trees E is close to M and therefore in particular, for every
$E_a \in M$
: By standard facts about k-maximal iteration trees E is close to M and therefore in particular, for every
![]() $b \in [\operatorname {\mathrm {lh}}(E)]^{<\omega }$
,
$b \in [\operatorname {\mathrm {lh}}(E)]^{<\omega }$
,
![]() $E_{b} \in \Sigma _{1}^{M}(M)$
. But since M is admissible and
$E_{b} \in \Sigma _{1}^{M}(M)$
. But since M is admissible and
![]() $\kappa < \delta $
, this implies that
$\kappa < \delta $
, this implies that
![]() $E_a \in M$
.
$E_a \in M$
.
Using
![]() $\Delta _{0}$
-collection, we have for every
$\Delta _{0}$
-collection, we have for every
![]() $h\in {^{[\kappa ]^{j}}} M \cap (M\vert \delta )$
and A such that
$h\in {^{[\kappa ]^{j}}} M \cap (M\vert \delta )$
and A such that
there is some
![]() $Y\in M$
such that
$Y\in M$
such that
Thus,
By another application of
![]() $\Delta _{0}$
-collection this gives us
$\Delta _{0}$
-collection this gives us
![]() $\beta < \operatorname {\mathrm {OR}}^M$
such that
$\beta < \operatorname {\mathrm {OR}}^M$
such that
It now easily follows that
![]() $g^{\prime }$
is bounded by
$g^{\prime }$
is bounded by
![]() $M^\prime \vert i(\beta )$
.
$M^\prime \vert i(\beta )$
.
In the case that E is finitely generated this argument shows that
![]() $M^\prime \models \text {KP}$
. Thus, we may assume that E is not finitely generated. In this case,
$M^\prime \models \text {KP}$
. Thus, we may assume that E is not finitely generated. In this case,
![]() $M^{\prime }$
is the direct limit of
$M^{\prime }$
is the direct limit of
where
![]() $\pi _{ab}$
is the canonical factor embedding. For
$\pi _{ab}$
is the canonical factor embedding. For
![]() $a\in [\nu (E)]^{<\omega }$
let
$a\in [\nu (E)]^{<\omega }$
let
![]() $X_{a}:=\pi _{a\infty }[\text {Ult}_{0}(M,E_{a})]$
. By Łoś’s Theorem it follows that
$X_{a}:=\pi _{a\infty }[\text {Ult}_{0}(M,E_{a})]$
. By Łoś’s Theorem it follows that
![]() $\pi _{a\infty }:\text {Ult}_{0}(M,E_{a})\rightarrow M^{\prime }$
is
$\pi _{a\infty }:\text {Ult}_{0}(M,E_{a})\rightarrow M^{\prime }$
is
![]() $\Sigma _{1}$
-elementary.
$\Sigma _{1}$
-elementary.
Suppose now that
![]() $f ^\prime \in \Sigma _{1}^{M^{\prime }} (M^{\prime })$
. There is some
$f ^\prime \in \Sigma _{1}^{M^{\prime }} (M^{\prime })$
. There is some
![]() $a \in [\nu (E)]^{<\omega }$
such that
$a \in [\nu (E)]^{<\omega }$
such that
![]() ${f^\prime \in \Sigma _1^{M^\prime } (\{ p^\prime \})}$
for some
${f^\prime \in \Sigma _1^{M^\prime } (\{ p^\prime \})}$
for some
![]() $p^\prime \in X_{a}$
. Let
$p^\prime \in X_{a}$
. Let
![]() $p = \pi _{a \infty }^{-1}(p^\prime )$
and let f be the function, which is defined over
$p = \pi _{a \infty }^{-1}(p^\prime )$
and let f be the function, which is defined over
![]() $\text {Ult}_{0}(M,E_a)$
via the parameter p, as
$\text {Ult}_{0}(M,E_a)$
via the parameter p, as
![]() $f^\prime $
is defined over
$f^\prime $
is defined over
![]() $M^\prime $
via the parameter
$M^\prime $
via the parameter
![]() $p^\prime $
. By the claim we have that
$p^\prime $
. By the claim we have that
![]() $f \in \text {Ult}_{0}(M,E_a)$
. But this means that
$f \in \text {Ult}_{0}(M,E_a)$
. But this means that
![]() $f^\prime \in M^\prime $
. Thus, by Lemma 3,
$f^\prime \in M^\prime $
. Thus, by Lemma 3,
![]() $M^\prime $
is admissible.
$M^\prime $
is admissible.
Case 2.
 $\operatorname {\mathrm {lh}}(\mathcal {T}) = \theta $
is a limit ordinal.
$\operatorname {\mathrm {lh}}(\mathcal {T}) = \theta $
is a limit ordinal.
This is proven much as in the case that
![]() $\theta = \zeta +1$
is a successor ordinal and
$\theta = \zeta +1$
is a successor ordinal and
![]() $E_\zeta $
is not finitely generated.
$E_\zeta $
is not finitely generated.
This finishes the proof of Claim 1.
Claim 2. Suppose
![]() $\mathcal {M}_{\theta }^{\mathcal {T}}$
is an admissible passive premouse with a largest, regular, and uncountable cardinal. Then so is
$\mathcal {M}_{\theta }^{\mathcal {T}}$
is an admissible passive premouse with a largest, regular, and uncountable cardinal. Then so is
![]() $\mathcal {M}_{\eta }^{*\mathcal {T}}$
.
$\mathcal {M}_{\eta }^{*\mathcal {T}}$
.
Proof. Again we argue by induction on
![]() $\theta $
. Suppose first that
$\theta $
. Suppose first that
![]() $\theta =\zeta +1$
and let
$\theta =\zeta +1$
and let
![]() $\mathcal {M}^{\mathcal {T}}_\theta = M^\prime $
and
$\mathcal {M}^{\mathcal {T}}_\theta = M^\prime $
and
![]() $M = \mathcal {M}_\theta ^{*\mathcal {T}}$
. Again, by standard arguments we may assume that M is a premouse with a largest, regular, and uncountable cardinal
$M = \mathcal {M}_\theta ^{*\mathcal {T}}$
. Again, by standard arguments we may assume that M is a premouse with a largest, regular, and uncountable cardinal
![]() $\delta $
. It suffices to see that M is admissible for which in turn it suffices to see that
$\delta $
. It suffices to see that M is admissible for which in turn it suffices to see that
![]() $\Delta _0$
-collection holds in M. Suppose for the sake of contradiction that this is not true and let
$\Delta _0$
-collection holds in M. Suppose for the sake of contradiction that this is not true and let
![]() $\eta < \operatorname {\mathrm {OR}}^M$
witness the least failure of
$\eta < \operatorname {\mathrm {OR}}^M$
witness the least failure of
![]() $\Delta _{0}$
-collection, i.e.,
$\Delta _{0}$
-collection, i.e.,
-
1. there is a
 $\Sigma _{1}$
-formula
$\Sigma _{1}$
-formula
 $\varphi $
and
$\varphi $
and
 $p\in M$
such that
$p\in M$
such that
 $M\models \forall \alpha <\eta \exists x\varphi (x,\alpha ,p)$
, but there is no
$M\models \forall \alpha <\eta \exists x\varphi (x,\alpha ,p)$
, but there is no
 $z\in M$
such that
$z\in M$
such that
 $M\models \forall \alpha <\eta \exists x\in z\varphi (x,\alpha ,p)$
, and
$M\models \forall \alpha <\eta \exists x\in z\varphi (x,\alpha ,p)$
, and -
2. for all
 $\Sigma _1$
-formulas
$\Sigma _1$
-formulas
 $\psi $
and
$\psi $
and
 $q \in M$
we have that if
$q \in M$
we have that if
 $\gamma < \eta $
and
$\gamma < \eta $
and
 $M \models \forall \alpha < \gamma \exists x \psi (x,q)$
, then there is
$M \models \forall \alpha < \gamma \exists x \psi (x,q)$
, then there is
 $z \in M$
such that
$z \in M$
such that
 $M \models \forall \alpha < \gamma \exists x \in z \psi (x,q)$
.
$M \models \forall \alpha < \gamma \exists x \in z \psi (x,q)$
.
Let
![]() $n = \deg _\theta ^{\mathcal {T}}$
so that
$n = \deg _\theta ^{\mathcal {T}}$
so that
![]() $M^\prime = \text {Ult}_{n}(M,E)$
, where
$M^\prime = \text {Ult}_{n}(M,E)$
, where
![]() $E = E_{\zeta }^{\mathcal {T}}$
. As before we may assume that
$E = E_{\zeta }^{\mathcal {T}}$
. As before we may assume that
![]() $n\leq 1$
. Let
$n\leq 1$
. Let
![]() $i:=i_{\theta }^{*\mathcal {T}}:M\rightarrow M^{\prime }$
be the ultrapower map and let
$i:=i_{\theta }^{*\mathcal {T}}:M\rightarrow M^{\prime }$
be the ultrapower map and let
![]() $\delta ^{\prime }=i(\delta )$
be the largest cardinal of
$\delta ^{\prime }=i(\delta )$
be the largest cardinal of
![]() $M^{\prime }$
. Note that we can no longer assume that i is both a
$M^{\prime }$
. Note that we can no longer assume that i is both a
![]() $0$
- and a
$0$
- and a
![]() $1$
-embedding, unlike in Claim 1.
$1$
-embedding, unlike in Claim 1.
Case 1.
 $n=1$
.
$n=1$
.
Note that it suffices to see that
![]() $M^{\prime }\models \forall \alpha <i(\eta )\exists x \varphi (x,\alpha ,i(p))$
because then by the admissibility of
$M^{\prime }\models \forall \alpha <i(\eta )\exists x \varphi (x,\alpha ,i(p))$
because then by the admissibility of
![]() $M^{\prime }$
,
$M^{\prime }$
,
![]() $M^{\prime }\models \exists z^{\prime }\forall \alpha <i(\eta )\exists x\in z^{\prime }\varphi (x,\alpha ,i(p))$
and so by the elementarity of i there is a bound in M. Note that i is a
$M^{\prime }\models \exists z^{\prime }\forall \alpha <i(\eta )\exists x\in z^{\prime }\varphi (x,\alpha ,i(p))$
and so by the elementarity of i there is a bound in M. Note that i is a
![]() $1$
-embedding and therefore
$1$
-embedding and therefore
![]() $r\Sigma _2$
-elementary. But this means that
$r\Sigma _2$
-elementary. But this means that
![]() $M^{\prime }\models \forall \alpha <i(\eta )\exists x \varphi (x,\alpha ,i(p))$
.
$M^{\prime }\models \forall \alpha <i(\eta )\exists x \varphi (x,\alpha ,i(p))$
.
Case 2.
 $n=0$
.
$n=0$
.
Let
![]() $\eta ^{\prime }:=\sup (i[\eta ])$
and note that
$\eta ^{\prime }:=\sup (i[\eta ])$
and note that
![]() $\eta ^{\prime }$
is a limit ordinal. We claim that for every
$\eta ^{\prime }$
is a limit ordinal. We claim that for every
![]() $\alpha < \eta ^\prime $
,
$\alpha < \eta ^\prime $
,
![]() $M^\prime \models \exists x \varphi (x,\alpha ,i(p))$
. Suppose otherwise and let
$M^\prime \models \exists x \varphi (x,\alpha ,i(p))$
. Suppose otherwise and let
![]() $\alpha ^{\prime }<\eta ^{\prime }$
be a counterexample, i.e.
$\alpha ^{\prime }<\eta ^{\prime }$
be a counterexample, i.e.
Let
![]() $\alpha <\eta $
be such that
$\alpha <\eta $
be such that
![]() $i(\alpha )>\alpha ^{\prime }$
. Note that since
$i(\alpha )>\alpha ^{\prime }$
. Note that since
![]() $\eta $
is the minimal failure of
$\eta $
is the minimal failure of
![]() $\Delta _{0}$
-collection in M,
$\Delta _{0}$
-collection in M,
But this is a
![]() $\Sigma _{1}$
-statement, so that
$\Sigma _{1}$
-statement, so that
But then in particular,
Contradiction! Therefore, by
![]() $\Delta _{0}$
-collection in
$\Delta _{0}$
-collection in
![]() $M^\prime $
, there is
$M^\prime $
, there is
![]() $\beta ^{\prime }<\operatorname {\mathrm {OR}}^{M^{\prime }}$
such that
$\beta ^{\prime }<\operatorname {\mathrm {OR}}^{M^{\prime }}$
such that
![]() $M^{\prime }\models \forall \alpha <\eta ^{\prime }\exists x\in (M^{\prime }\vert \beta ^{\prime })\varphi (x,\alpha ,i(p)).$
Since i is cofinal, we may assume without loss of generality that
$M^{\prime }\models \forall \alpha <\eta ^{\prime }\exists x\in (M^{\prime }\vert \beta ^{\prime })\varphi (x,\alpha ,i(p)).$
Since i is cofinal, we may assume without loss of generality that
![]() $\beta ^{\prime }\in \operatorname {\mathrm {ran}}(i)$
. Let
$\beta ^{\prime }\in \operatorname {\mathrm {ran}}(i)$
. Let
![]() $\beta <\operatorname {\mathrm {OR}}^{M}$
be such that
$\beta <\operatorname {\mathrm {OR}}^{M}$
be such that
![]() $i(\beta )=\beta ^{\prime }$
. We claim that
$i(\beta )=\beta ^{\prime }$
. We claim that
which would be a contradiction! So suppose that there is
![]() $\alpha <\eta $
such that
$\alpha <\eta $
such that
This is a
![]() $\Delta _0$
statement, so that
$\Delta _0$
statement, so that
Contradiction!
Now let us suppose that
![]() $\theta $
is a limit ordinal. In the case that there is some
$\theta $
is a limit ordinal. In the case that there is some
![]() $\gamma \in b\cap \theta $
such that for all
$\gamma \in b\cap \theta $
such that for all
![]() $\xi \in (\gamma ,\theta )\cap b$
,
$\xi \in (\gamma ,\theta )\cap b$
,
![]() $\deg _\xi ^{\mathcal {T}} \geq 1$
, we can argue as in Case 1 of the successor case. If otherwise we can use the argument from Case 2 of the successor case, since
$\deg _\xi ^{\mathcal {T}} \geq 1$
, we can argue as in Case 1 of the successor case. If otherwise we can use the argument from Case 2 of the successor case, since
![]() $i_{\gamma \theta }^{\mathcal {T}}$
will be cofinal.
$i_{\gamma \theta }^{\mathcal {T}}$
will be cofinal.
This completes the proof of the lemma.
If we would not require
![]() $\delta $
to be regular in the statement of Lemma 15, the lemma would be provably false as the following example shows.
$\delta $
to be regular in the statement of Lemma 15, the lemma would be provably false as the following example shows.
Example 16. Let M be a
![]() $1$
-sound premouse such that
$1$
-sound premouse such that
![]() $M\models \text {KP}$
. Suppose that M has a largest cardinal
$M\models \text {KP}$
. Suppose that M has a largest cardinal
![]() $\delta>\omega $
such that for some
$\delta>\omega $
such that for some
![]() $\kappa <\delta $
,
$\kappa <\delta $
,
![]() $\operatorname {\mathrm {cof}}^{M}(\delta )=\kappa $
and there is an M-total
$\operatorname {\mathrm {cof}}^{M}(\delta )=\kappa $
and there is an M-total
![]() $E\in \mathbb {E}^{M}$
such that
$E\in \mathbb {E}^{M}$
such that
![]() $\operatorname {\mathrm {crit}}(E)=\kappa $
. Let
$\operatorname {\mathrm {crit}}(E)=\kappa $
. Let
![]() $\pi :M\rightarrow \text {Ult}_{1}(M,E)$
be the ultrapower embedding.
$\pi :M\rightarrow \text {Ult}_{1}(M,E)$
be the ultrapower embedding.
Then
![]() $\pi $
is discontinuous at
$\pi $
is discontinuous at
![]() $\delta $
so that
$\delta $
so that
![]() $\pi (\delta )>\sup (\pi [\delta ])$
. However, since
$\pi (\delta )>\sup (\pi [\delta ])$
. However, since
![]() $\pi $
is a
$\pi $
is a
![]() $1$
-embedding,
$1$
-embedding,
![]() $\rho _{1}^{M}=\sup (\pi [\delta ])$
. But
$\rho _{1}^{M}=\sup (\pi [\delta ])$
. But
![]() $\pi (\delta )$
is the largest cardinal of
$\pi (\delta )$
is the largest cardinal of
![]() $\text {Ult}_{1}(M,E)$
. So by Lemma 4,
$\text {Ult}_{1}(M,E)$
. So by Lemma 4,
![]() $\text {Ult}_{1}(M,E) \not \models \text {KP}$
.
$\text {Ult}_{1}(M,E) \not \models \text {KP}$
.
In this subsection we have established the following (cf. [Reference Steel11, Chapter 7.2]).
Theorem 17. Let
![]() $k\leq \omega $
and suppose that M is a k-sound,
$k\leq \omega $
and suppose that M is a k-sound,
![]() $(k,\vert M\vert ^{+}+1)$
-iterable admissible passive premouse with a largest, regular, and uncountable cardinal
$(k,\vert M\vert ^{+}+1)$
-iterable admissible passive premouse with a largest, regular, and uncountable cardinal
![]() $\delta $
. Suppose that
$\delta $
. Suppose that
![]() $\delta $
is Woodin in M and let
$\delta $
is Woodin in M and let
![]() $X\subset \vert M \vert $
. Then there is a k-maximal iteration tree
$X\subset \vert M \vert $
. Then there is a k-maximal iteration tree
![]() $\mathcal {T}$
on M with last model
$\mathcal {T}$
on M with last model
![]() $\mathcal {M}_\infty ^{\mathcal {T}}$
, which does not drop in model anywhere, such that X is generic over
$\mathcal {M}_\infty ^{\mathcal {T}}$
, which does not drop in model anywhere, such that X is generic over
![]() $\mathcal {M}_{\infty }^{\mathcal {T}}$
for the extender algebra of
$\mathcal {M}_{\infty }^{\mathcal {T}}$
for the extender algebra of
![]() $\mathcal {M}_\infty ^{\mathcal {T}}$
and
$\mathcal {M}_\infty ^{\mathcal {T}}$
and
![]() $\mathcal {M}_{\infty }^{\mathcal {T}}[X]\models \text {KP}$
.
$\mathcal {M}_{\infty }^{\mathcal {T}}[X]\models \text {KP}$
.
2.3 A version of the truncation Lemma
For the proof of Lemma 24, we need a version of the Truncation Lemma for premice. Recall the following coarse definition. If M is a possibly ill-founded structure in some signature extending
![]() $\mathcal {L}_{\dot {\in }}$
, we call
$\mathcal {L}_{\dot {\in }}$
, we call
the wellfounded part of M. By [Reference Barwise1] and Problem 5.27 of [Reference Schindler8], if
![]() $M \models \text {KP}$
, then
$M \models \text {KP}$
, then
![]() $\text {wfp}(M) \models \text {KP}$
. We aim to show something similar in the case that M is an ill-founded premouse.
$\text {wfp}(M) \models \text {KP}$
. We aim to show something similar in the case that M is an ill-founded premouse.
Definition 18. Let
![]() $M = (\lfloor M \rfloor , \in ^M, \mathbb {E}^M)$
be an
$M = (\lfloor M \rfloor , \in ^M, \mathbb {E}^M)$
be an
![]() $\mathcal {L}_{\dot {\in }, \dot {E}}$
-structure. We say that
$\mathcal {L}_{\dot {\in }, \dot {E}}$
-structure. We say that
![]() ${M \models "V=L[E]"}$
, if M models the Axiom of Extensionality, the Axiom of Foundation, and
${M \models "V=L[E]"}$
, if M models the Axiom of Extensionality, the Axiom of Foundation, and
where
![]() $S_\alpha [\dot {E}]$
is the refinement of the
$S_\alpha [\dot {E}]$
is the refinement of the
![]() $J[\dot {E}]$
-hierarchy as described in Chapter 5 of [Reference Schindler8].
$J[\dot {E}]$
-hierarchy as described in Chapter 5 of [Reference Schindler8].
Note that the second conjunct of 2.6 makes sure that the model is an actual instance of its internal J-hierarchy.
Definition 19. Let
![]() $M = (\lfloor M \rfloor , \in ^M, \mathbb {E}^M)$
be an
$M = (\lfloor M \rfloor , \in ^M, \mathbb {E}^M)$
be an
![]() $\mathcal {L}_{\in , \dot {E}}$
-structure such that
$\mathcal {L}_{\in , \dot {E}}$
-structure such that
![]() $M \models "V = L[E]"$
and
$M \models "V = L[E]"$
and
![]() $\text {wfp} (M)$
is transitive. Letting
$\text {wfp} (M)$
is transitive. Letting
![]() $\text {wfo}(M) = \operatorname {\mathrm {OR}} \cap \text {wfp}(M)$
, we call
$\text {wfo}(M) = \operatorname {\mathrm {OR}} \cap \text {wfp}(M)$
, we call
the wellfounded cut of M.
The next lemma is the version of the Truncation Lemma we need for the proof of Lemma 24. The proof is essentially identical to the proof of Proposition 2.4 in [Reference Hachtman3].
Lemma 20. Let
![]() $M = (\lfloor M \rfloor , \in ^M, \mathbb {E}^M)$
be an ill-founded
$M = (\lfloor M \rfloor , \in ^M, \mathbb {E}^M)$
be an ill-founded
![]() $\mathcal {L}_{\in , \dot {E}}$
-structure such that
$\mathcal {L}_{\in , \dot {E}}$
-structure such that
![]() ${M \models "V = L[E]"}$
and
${M \models "V = L[E]"}$
and
![]() $\text {wfp} (M)$
is transitive. Then
$\text {wfp} (M)$
is transitive. Then
![]() $\text {wfc}(M) \models \text {KP}$
.
$\text {wfc}(M) \models \text {KP}$
.
Proof. We may assume that
![]() $\omega \in \text {wfc}(M)$
, as otherwise
$\omega \in \text {wfc}(M)$
, as otherwise
![]() $\text {wfc}(M) = L_\omega $
which is clearly admissible. It suffices to see that
$\text {wfc}(M) = L_\omega $
which is clearly admissible. It suffices to see that
![]() $\text {wfc}(M) \models \Delta _0 \text {-Collection}$
. By induction, it easily follows that for
$\text {wfc}(M) \models \Delta _0 \text {-Collection}$
. By induction, it easily follows that for
![]() $\alpha < \text {wfo}(M)$
,
$\alpha < \text {wfo}(M)$
,
![]() $S_\alpha ^{\mathbb {E}^M} = (S_\alpha )^M \in \text {wfp}(M)$
, so that
$S_\alpha ^{\mathbb {E}^M} = (S_\alpha )^M \in \text {wfp}(M)$
, so that
![]() $\text {wfc} (M) \subseteq \text {wfp}(M)$
. Let
$\text {wfc} (M) \subseteq \text {wfp}(M)$
. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Sigma _0$
formula and
$\Sigma _0$
formula and
![]() $a,p \in \text {wfc} (M)$
such that
$a,p \in \text {wfc} (M)$
such that
Note that by
![]() $\Sigma _1$
upwards absoluteness this holds in M. Let
$\Sigma _1$
upwards absoluteness this holds in M. Let
![]() $\gamma $
be a non-standard ordinal of M. In
$\gamma $
be a non-standard ordinal of M. In
![]() $S_\gamma ^M$
, we may define a function F with
$S_\gamma ^M$
, we may define a function F with
![]() $\operatorname {\mathrm {dom}}(F) = a$
such that for
$\operatorname {\mathrm {dom}}(F) = a$
such that for
![]() $x \in a$
,
$x \in a$
,
Since
![]() $\text {wfc} (M) \subseteq S_\gamma ^M$
, it follows by
$\text {wfc} (M) \subseteq S_\gamma ^M$
, it follows by
![]() $\Sigma _1$
upwards absoluteness that
$\Sigma _1$
upwards absoluteness that
![]() $F(x) < \text {wfo}(M)$
. However, this means that
$F(x) < \text {wfo}(M)$
. However, this means that
![]() $\eta := \bigcup _{x \in a} F(x) \subset \text {wfo}(M)$
. Since F is definable over M, we must have that
$\eta := \bigcup _{x \in a} F(x) \subset \text {wfo}(M)$
. Since F is definable over M, we must have that
![]() $\eta < \text {wfo}(M)$
. This means that
$\eta < \text {wfo}(M)$
. This means that
Thus,
![]() $\text {wfc} (M) \models \text {KP}$
.
$\text {wfc} (M) \models \text {KP}$
.
3 Where the conjecture holds
In this section, we will show under the assumption that there is no transitive model of KP with a Woodin cardinal that Conjecture 1 holds. This will be a consequence of Theorem 26. Lemma 24 is the key insight for proving Theorem 26. First, let us recall some well-known basic properties of weasels and their coiterations.
The following theorem from [Reference Steel10] guarantees that the coiteration of two
![]() $\Omega +1$
-iterable weasels of height
$\Omega +1$
-iterable weasels of height
![]() $\Omega $
is successful.
$\Omega $
is successful.
Theorem 21. Let
![]() $\kappa $
be an inaccessible cardinal. Let
$\kappa $
be an inaccessible cardinal. Let
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
be premice such that
$\mathcal {N}$
be premice such that
![]() $\operatorname {\mathrm {OR}}^{\mathcal {M}}=\operatorname {\mathrm {OR}}^{\mathcal {N}}=\kappa $
. Let
$\operatorname {\mathrm {OR}}^{\mathcal {M}}=\operatorname {\mathrm {OR}}^{\mathcal {N}}=\kappa $
. Let
![]() $(\mathcal {T},\mathcal {U})$
be a successful coiteration of
$(\mathcal {T},\mathcal {U})$
be a successful coiteration of
![]() $(\mathcal {M},\mathcal {N})$
. Then
$(\mathcal {M},\mathcal {N})$
. Then
![]() $\max \{\operatorname {\mathrm {lh}}(\mathcal {T}), \operatorname {\mathrm {lh}}(\mathcal {U})\}\leq \kappa +1$
. Moreover, setting
$\max \{\operatorname {\mathrm {lh}}(\mathcal {T}), \operatorname {\mathrm {lh}}(\mathcal {U})\}\leq \kappa +1$
. Moreover, setting
![]() $\operatorname {\mathrm {lh}}(\mathcal {T})=\theta +1$
and
$\operatorname {\mathrm {lh}}(\mathcal {T})=\theta +1$
and
![]() $\operatorname {\mathrm {lh}}(\mathcal {U})=\gamma +1$
, either
$\operatorname {\mathrm {lh}}(\mathcal {U})=\gamma +1$
, either
-
1.
 $D^{\mathcal {T}}\cap [0,\theta ]^{\mathcal {T}}=\emptyset $
,
$D^{\mathcal {T}}\cap [0,\theta ]^{\mathcal {T}}=\emptyset $
,
 $i_{0,\theta }^{\mathcal {T}}[\kappa ]\subset \kappa $
,
$i_{0,\theta }^{\mathcal {T}}[\kappa ]\subset \kappa $
,
 $\mathcal {M}_{\theta }^{\mathcal {T}}\unlhd \mathcal {M}_{\gamma }^{\mathcal {U}}$
, and
$\mathcal {M}_{\theta }^{\mathcal {T}}\unlhd \mathcal {M}_{\gamma }^{\mathcal {U}}$
, and
 $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\theta }^{\mathcal {T}}}=\kappa $
, or
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\theta }^{\mathcal {T}}}=\kappa $
, or -
2.
 $D^{\mathcal {U}}\cap [0,\gamma ]^{\mathcal {U}}=\emptyset $
,
$D^{\mathcal {U}}\cap [0,\gamma ]^{\mathcal {U}}=\emptyset $
,
 $i_{0,\gamma }^{\mathcal {U}}[\kappa ]\subset \kappa $
,
$i_{0,\gamma }^{\mathcal {U}}[\kappa ]\subset \kappa $
,
 $\mathcal {M}_{\gamma }^{\mathcal {U}}\unlhd \mathcal {M}_{\theta }^{\mathcal {T}}$
, and
$\mathcal {M}_{\gamma }^{\mathcal {U}}\unlhd \mathcal {M}_{\theta }^{\mathcal {T}}$
, and
 $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\gamma }^{\mathcal {U}}}=\kappa $
.
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\gamma }^{\mathcal {U}}}=\kappa $
.
The next lemma collects basic facts about iteration trees whose proof is well-known.
Lemma 22. Let
![]() $\kappa $
be a regular and uncountable cardinal. Let
$\kappa $
be a regular and uncountable cardinal. Let
![]() $\mathcal {M}$
be a premouse such that
$\mathcal {M}$
be a premouse such that
![]() $\operatorname {\mathrm {OR}}^{\mathcal {M}}=\kappa $
and let
$\operatorname {\mathrm {OR}}^{\mathcal {M}}=\kappa $
and let
![]() $\mathcal {T}$
be a
$\mathcal {T}$
be a
![]() $0$
-maximal iteration tree on
$0$
-maximal iteration tree on
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\operatorname {\mathrm {lh}}(\mathcal {T})=\kappa +1$
. Let
$\operatorname {\mathrm {lh}}(\mathcal {T})=\kappa +1$
. Let
![]() $b := [0,\kappa ]^{\mathcal {T}}$
. Then the following hold:
$b := [0,\kappa ]^{\mathcal {T}}$
. Then the following hold:
-
1. if
 $b \cap D^{\mathcal {T}} = \emptyset $
and
$b \cap D^{\mathcal {T}} = \emptyset $
and
 $i_{0\kappa }^{\mathcal {T}}[\kappa ]\subset \kappa $
, then there is a club
$i_{0\kappa }^{\mathcal {T}}[\kappa ]\subset \kappa $
, then there is a club
 $C_1 \subset b$
such that for all
$C_1 \subset b$
such that for all
 $\alpha \in C_1 \cap b$
,
$\alpha \in C_1 \cap b$
,
 $i_{0\alpha }^{\mathcal {T}}[\alpha ]\subset \alpha $
,
$i_{0\alpha }^{\mathcal {T}}[\alpha ]\subset \alpha $
, -
2. if
 $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\alpha }^{\mathcal {T}}} \leq \kappa $
for all
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\alpha }^{\mathcal {T}}} \leq \kappa $
for all
 $\alpha <\kappa $
, then there is a club
$\alpha <\kappa $
, then there is a club
 $C_2 \subset b$
such that for all
$C_2 \subset b$
such that for all
 $\alpha \in C_2$
,
$\alpha \in C_2$
,
 $\alpha =\sup \{\operatorname {\mathrm {lh}}(E_{\beta }^{\mathcal {T}}):\beta <\alpha \}$
, and
$\alpha =\sup \{\operatorname {\mathrm {lh}}(E_{\beta }^{\mathcal {T}}):\beta <\alpha \}$
, and -
3. if
 $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\alpha }^{\mathcal {T}}} \leq \kappa $
for all
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\alpha }^{\mathcal {T}}} \leq \kappa $
for all
 $\alpha <\kappa $
, and
$\alpha <\kappa $
, and
 $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\kappa }^{\mathcal {T}}}>\kappa $
, then there is a club
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\kappa }^{\mathcal {T}}}>\kappa $
, then there is a club
 $C_3 \subset b$
such that for all
$C_3 \subset b$
such that for all
 $\alpha \in C_3$
,
$\alpha \in C_3$
,
 $\alpha> \sup (D^{\mathcal {U}} \cap b)$
,
$\alpha> \sup (D^{\mathcal {U}} \cap b)$
,
 $i_{\alpha \kappa }^{\mathcal {T}}(\alpha )=\kappa $
and
$i_{\alpha \kappa }^{\mathcal {T}}(\alpha )=\kappa $
and
 $\operatorname {\mathrm {crit}}(i_{\alpha \kappa }^{\mathcal {T}})=\alpha $
.
$\operatorname {\mathrm {crit}}(i_{\alpha \kappa }^{\mathcal {T}})=\alpha $
.
We need the following version of the
![]() $\Sigma _{1}^{1}$
-Bounding Theorem in order to prove Lemma 24.
$\Sigma _{1}^{1}$
-Bounding Theorem in order to prove Lemma 24.
Theorem 23. Let
![]() $x \in {{^\omega }\omega }$
and suppose that
$x \in {{^\omega }\omega }$
and suppose that
![]() $A\subset \text {WO}$
is
$A\subset \text {WO}$
is
![]() $\Sigma _{1}^{1}(x)$
-definable, where
$\Sigma _{1}^{1}(x)$
-definable, where
![]() $\text {WO} \subset {{^\omega }\omega }$
is the set of reals coding well orderings of
$\text {WO} \subset {{^\omega }\omega }$
is the set of reals coding well orderings of
![]() $\omega $
. Then
$\omega $
. Then
where
![]() $R_{y}\subset \omega \times \omega $
is the relation coded by y and
$R_{y}\subset \omega \times \omega $
is the relation coded by y and
![]() $\omega _{1}^{\operatorname {\mathrm {CK}}}(x)$
is the least ordinal
$\omega _{1}^{\operatorname {\mathrm {CK}}}(x)$
is the least ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $L_\alpha [x]\models \text {KP}$
.Footnote
8
$L_\alpha [x]\models \text {KP}$
.Footnote
8
The proof of Theorem 23 is basically a refinement of the Kunen–Martin Theorem, which may be found in [Reference Moschovakis6, p. 75].
Lemma 24. Let M be a premouse such that
![]() $\delta $
is a regular, uncountable cardinal of M and
$\delta $
is a regular, uncountable cardinal of M and
![]() $M \models "\delta ^{+} \text { exists}"$
. Suppose that M is
$M \models "\delta ^{+} \text { exists}"$
. Suppose that M is
![]() $(0,\delta +1)$
-iterable, and there is no initial segment of M which models KP + “there is a Woodin cardinal”. Let
$(0,\delta +1)$
-iterable, and there is no initial segment of M which models KP + “there is a Woodin cardinal”. Let
![]() $\mathcal {U}$
be a
$\mathcal {U}$
be a
![]() $0$
-maximal iteration tree on M such that
$0$
-maximal iteration tree on M such that
-
•
 $\operatorname {\mathrm {lh}}(\mathcal {U})=\delta +1$
,
$\operatorname {\mathrm {lh}}(\mathcal {U})=\delta +1$
, -
•
 $\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}}):\alpha <\delta \}=\delta $
,
$\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}}):\alpha <\delta \}=\delta $
, -
•
 $b\cap D^{U}=\emptyset $
, where
$b\cap D^{U}=\emptyset $
, where
 $b:=[0,\delta ]^{\mathcal {U}}$
, i.e.,
$b:=[0,\delta ]^{\mathcal {U}}$
, i.e.,
 $\mathcal {U}$
is non-dropping on its main branch, and
$\mathcal {U}$
is non-dropping on its main branch, and -
•
 $i_{0\delta }^{\mathcal {U}}(\delta )=\delta $
.
$i_{0\delta }^{\mathcal {U}}(\delta )=\delta $
.
Then
![]() $i_{0\delta }^{\mathcal {U}}(\delta ^{+M})=\delta ^{+M}$
.
$i_{0\delta }^{\mathcal {U}}(\delta ^{+M})=\delta ^{+M}$
.
Proof. Suppose otherwise, and let
![]() $\mathcal {U}$
be a counterexample. Let
$\mathcal {U}$
be a counterexample. Let
![]() $\xi <\delta ^{+M}$
be such that
$\xi <\delta ^{+M}$
be such that
![]() $i_{0\delta }^{\mathcal {U}}(\xi )>\delta ^{+M}$
and
$i_{0\delta }^{\mathcal {U}}(\xi )>\delta ^{+M}$
and
![]() $\rho _{\omega }^{M\vert \xi }=\delta $
. Note that such
$\rho _{\omega }^{M\vert \xi }=\delta $
. Note that such
![]() $\xi $
exists since
$\xi $
exists since
![]() $i_{0\delta }^{\mathcal {U}}$
is continuous at
$i_{0\delta }^{\mathcal {U}}$
is continuous at
![]() $\delta ^{+M}$
, as
$\delta ^{+M}$
, as
![]() $\delta ^{+M}$
and its images are not of measurable cofinality in any
$\delta ^{+M}$
and its images are not of measurable cofinality in any
![]() $\mathcal {M}_\alpha ^{\mathcal {U}}$
for
$\mathcal {M}_\alpha ^{\mathcal {U}}$
for
![]() $\alpha \in [0,\delta )^{\mathcal {U}}$
and
$\alpha \in [0,\delta )^{\mathcal {U}}$
and
![]() $\mathcal {U}$
is
$\mathcal {U}$
is
![]() $0$
-maximal. Moreover, it is a standard fact that the ordinals
$0$
-maximal. Moreover, it is a standard fact that the ordinals
![]() $\eta $
such that
$\eta $
such that
![]() $\rho _{\omega }^{M\vert \eta }=\delta $
are cofinal in
$\rho _{\omega }^{M\vert \eta }=\delta $
are cofinal in
![]() $\delta ^{+M}$
. We also assume that
$\delta ^{+M}$
. We also assume that
![]() $\xi>\operatorname {\mathrm {OR}}^{Q}$
, where
$\xi>\operatorname {\mathrm {OR}}^{Q}$
, where
![]() $Q\lhd M$
is least such that
$Q\lhd M$
is least such that
![]() $J(Q)\models "\delta \text { is not Woodin}"$
. Note that Q exists and
$J(Q)\models "\delta \text { is not Woodin}"$
. Note that Q exists and
![]() $\operatorname {\mathrm {OR}}^{Q}<\delta ^{+M}$
, since there is no initial segment of M which models KP and has
$\operatorname {\mathrm {OR}}^{Q}<\delta ^{+M}$
, since there is no initial segment of M which models KP and has
![]() $\delta $
as a Woodin.
$\delta $
as a Woodin.
Let
![]() $g\subset \operatorname {\mathrm {Col}}(\omega ,\delta )$
be V-generic. In particular, g is also M-generic. Let
$g\subset \operatorname {\mathrm {Col}}(\omega ,\delta )$
be V-generic. In particular, g is also M-generic. Let
![]() $x\in M[g]\cap {^{\omega }\omega }$
code
$x\in M[g]\cap {^{\omega }\omega }$
code
![]() $M\vert \xi +\omega $
.
$M\vert \xi +\omega $
.
Let us define in
![]() $V[g]$
the set
$V[g]$
the set
![]() $\bar {A}$
such that
$\bar {A}$
such that
![]() $\mathcal {T}\in \bar {A}$
if and only if
$\mathcal {T}\in \bar {A}$
if and only if
-
1.
 $\mathcal {T}$
is a
$\mathcal {T}$
is a
 $0$
-maximal putative iteration tree on
$0$
-maximal putative iteration tree on
 $M\vert \xi +\omega $
such that
$M\vert \xi +\omega $
such that
 $\operatorname {\mathrm {lh}}(\mathcal {T})=\delta +1$
$\operatorname {\mathrm {lh}}(\mathcal {T})=\delta +1$
-
2.
 $\mathcal {T}$
is non-dropping on its main branch,
$\mathcal {T}$
is non-dropping on its main branch, -
3.
 $\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}}):\alpha <\delta \}=\delta $
, and
$\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}}):\alpha <\delta \}=\delta $
, and -
4.
 $i_{0\delta }^{\mathcal {T}}(\delta )=\delta $
, thus in particular,
$i_{0\delta }^{\mathcal {T}}(\delta )=\delta $
, thus in particular,
 $\mathcal {M}_{\delta }^{\mathcal {T}}\vert \delta \in \operatorname {\mathrm {wfp}}(\mathcal {M}_{\delta }^{\mathcal {T}})$
.
$\mathcal {M}_{\delta }^{\mathcal {T}}\vert \delta \in \operatorname {\mathrm {wfp}}(\mathcal {M}_{\delta }^{\mathcal {T}})$
.
Note that if
![]() $\mathcal {T} \in \bar {A}$
, then
$\mathcal {T} \in \bar {A}$
, then
![]() $\mathcal {T} \!\upharpoonright \! \delta $
is guided by Q-structures.
$\mathcal {T} \!\upharpoonright \! \delta $
is guided by Q-structures.
Claim 1. If
![]() $\mathcal {T}\in \bar {A}$
, then there is a Q-structure for
$\mathcal {T}\in \bar {A}$
, then there is a Q-structure for
![]() $\mathcal {T}\!\upharpoonright \!\delta $
in
$\mathcal {T}\!\upharpoonright \!\delta $
in
![]() $V[g]$
, i.e., there is
$V[g]$
, i.e., there is
![]() $\alpha <\operatorname {\mathrm {OR}}$
such that
$\alpha <\operatorname {\mathrm {OR}}$
such that
![]() $J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))\models "\delta =\delta (\mathcal {T}\!\upharpoonright \!\delta )\text { is not Woodin}"$
.
$J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))\models "\delta =\delta (\mathcal {T}\!\upharpoonright \!\delta )\text { is not Woodin}"$
.
Proof. Suppose that there is no Q-structure in
![]() $V[g]$
. This means that for all
$V[g]$
. This means that for all
![]() ${\alpha <\operatorname {\mathrm {OR}}}$
,
${\alpha <\operatorname {\mathrm {OR}}}$
,
![]() $J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))\models "\delta \text { is Woodin}"$
. Let
$J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))\models "\delta \text { is Woodin}"$
. Let
![]() $\alpha $
be least such that
$\alpha $
be least such that
![]() $J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))\models \text {KP}$
. Since
$J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))\models \text {KP}$
. Since
![]() $\delta $
is regular in
$\delta $
is regular in
![]() $L(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))$
, there is
$L(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))$
, there is
![]() $X\prec J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))$
such that
$X\prec J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))$
such that
![]() ${X\cap \delta \in \delta} $
. Let N be the transitive collapse of X; then by condensation,
${X\cap \delta \in \delta} $
. Let N be the transitive collapse of X; then by condensation,
![]() ${N \lhd \mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta )}$
. Note that since
${N \lhd \mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta )}$
. Note that since
![]() $\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta )=\bigcup _{\alpha \in [0,\delta )^{\mathcal {T}}}\mathcal {M}_{\alpha }^{\mathcal {T}}\vert \operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}})$
and by elementarity there is no initial segment of
$\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta )=\bigcup _{\alpha \in [0,\delta )^{\mathcal {T}}}\mathcal {M}_{\alpha }^{\mathcal {T}}\vert \operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}})$
and by elementarity there is no initial segment of
![]() $\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta )$
which models KP and has a Woodin. However, N models KP and has a Woodin. Contradiction!
$\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta )$
which models KP and has a Woodin. However, N models KP and has a Woodin. Contradiction!
Since for
![]() $\mathcal {T}\in \bar {A}$
there is a Q-structure for
$\mathcal {T}\in \bar {A}$
there is a Q-structure for
![]() $\mathcal {T}\!\upharpoonright \!\delta $
and
$\mathcal {T}\!\upharpoonright \!\delta $
and
![]() $\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}}):\alpha <\delta \}=\delta $
(and thus Q-structures for
$\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}}):\alpha <\delta \}=\delta $
(and thus Q-structures for
![]() $\mathcal {T}\!\upharpoonright \!\alpha $
with
$\mathcal {T}\!\upharpoonright \!\alpha $
with
![]() $\alpha <\delta $
are of ordinal height less than
$\alpha <\delta $
are of ordinal height less than
![]() $\delta $
) it follows by the usual absoluteness arguments that there is a unique cofinal well-founded branch b for
$\delta $
) it follows by the usual absoluteness arguments that there is a unique cofinal well-founded branch b for
![]() $\mathcal {T}\!\upharpoonright \!\delta $
in
$\mathcal {T}\!\upharpoonright \!\delta $
in
![]() $V[g]$
.
$V[g]$
.
However, at this point we do not know whether for
![]() $\mathcal {T}\in \bar {A}$
, the unique cofinal wellfounded branch of
$\mathcal {T}\in \bar {A}$
, the unique cofinal wellfounded branch of
![]() $\mathcal {T}\!\upharpoonright \!\delta $
was actually chosen, i.e. whether
$\mathcal {T}\!\upharpoonright \!\delta $
was actually chosen, i.e. whether
![]() $\mathcal {T}$
is an iteration tree. This is verified in the next claim.
$\mathcal {T}$
is an iteration tree. This is verified in the next claim.
Claim 2. If
![]() $\mathcal {T}\in \bar {A}$
, then
$\mathcal {T}\in \bar {A}$
, then
![]() $\mathcal {M}_{\delta }^{\mathcal {T}}$
is wellfounded.
$\mathcal {M}_{\delta }^{\mathcal {T}}$
is wellfounded.
Proof. Suppose otherwise. Let
![]() $\mathcal {T}\in \bar {A}$
be such that
$\mathcal {T}\in \bar {A}$
be such that
![]() $\mathcal {M}_{\delta }^{\mathcal {T}}$
is ill-founded. By 4 we have that
$\mathcal {M}_{\delta }^{\mathcal {T}}$
is ill-founded. By 4 we have that
![]() $\mathcal {M}_{\delta }^{\mathcal {T}}\vert \delta \in \operatorname {\mathrm {wfp}}(\mathcal {M}_{\delta }^{\mathcal {T}})$
. As we are assuming that
$\mathcal {M}_{\delta }^{\mathcal {T}}\vert \delta \in \operatorname {\mathrm {wfp}}(\mathcal {M}_{\delta }^{\mathcal {T}})$
. As we are assuming that
![]() $\mathcal {M}_{\delta }^{\mathcal {T}}$
is ill-founded, we may apply Lemma 20 and get that
$\mathcal {M}_{\delta }^{\mathcal {T}}$
is ill-founded, we may apply Lemma 20 and get that
![]() $\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}}) \models \text {KP}$
. To arrive at a contradiction, we distinguish two cases.
$\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}}) \models \text {KP}$
. To arrive at a contradiction, we distinguish two cases.
The first case is that
![]() $Q(c,\mathcal {T}\!\upharpoonright \!\delta )\lhd \text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
, where
$Q(c,\mathcal {T}\!\upharpoonright \!\delta )\lhd \text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
, where
![]() $c=[0,\delta ]^{\mathcal {T}}$
. Let b be the unique, cofinal, and wellfounded branch b for
$c=[0,\delta ]^{\mathcal {T}}$
. Let b be the unique, cofinal, and wellfounded branch b for
![]() $\mathcal {T}\!\upharpoonright \!\delta $
in
$\mathcal {T}\!\upharpoonright \!\delta $
in
![]() $V[g]$
. By
$V[g]$
. By
![]() $1$
-smallness, we have that
$1$
-smallness, we have that
![]() $Q(c,\mathcal {T}\!\upharpoonright \!\delta )=Q(b,\mathcal {T}\!\upharpoonright \!\delta )$
. Note that
$Q(c,\mathcal {T}\!\upharpoonright \!\delta )=Q(b,\mathcal {T}\!\upharpoonright \!\delta )$
. Note that
![]() $Q(b,\mathcal {T}\!\upharpoonright \!\delta ) \neq \mathcal {M}^{\mathcal {T}}_b$
, since otherwise there is a drop on b and thus
$Q(b,\mathcal {T}\!\upharpoonright \!\delta ) \neq \mathcal {M}^{\mathcal {T}}_b$
, since otherwise there is a drop on b and thus
![]() $Q(c,\mathcal {T}\!\upharpoonright \!\delta )$
is not sound, but
$Q(c,\mathcal {T}\!\upharpoonright \!\delta )$
is not sound, but
![]() $Q(c,\mathcal {T}\!\upharpoonright \!\delta ) \lhd \text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
, which would be a contradiction! But then by the Zipper Lemma, we have that
$Q(c,\mathcal {T}\!\upharpoonright \!\delta ) \lhd \text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
, which would be a contradiction! But then by the Zipper Lemma, we have that
![]() $\delta $
is Woodin in
$\delta $
is Woodin in
![]() $J(Q(b,\mathcal {T}\!\upharpoonright \!\delta ))$
. Contradiction!
$J(Q(b,\mathcal {T}\!\upharpoonright \!\delta ))$
. Contradiction!
The second case is that the Q-structure is not an element in
![]() $\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
. In this case we have that for every proper initial segment of
$\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
. In this case we have that for every proper initial segment of
![]() $\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
,
$\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
,
![]() $\mathcal {M}_{\delta }^{\mathcal {T}}$
thinks that
$\mathcal {M}_{\delta }^{\mathcal {T}}$
thinks that
![]() $\delta $
is Woodin in that segment. Moreover, by
$\delta $
is Woodin in that segment. Moreover, by
![]() $1$
-smallness we have that
$1$
-smallness we have that
![]() $\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}}) = J_{\beta }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))$
for some
$\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}}) = J_{\beta }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))$
for some
![]() $\beta $
. But this means that
$\beta $
. But this means that
![]() $\delta $
is Woodin in
$\delta $
is Woodin in
![]() $\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
.
$\text {wfc}(\mathcal {M}_{\delta }^{\mathcal {T}})$
.
Let b be unique cofinal and wellfounded branch b for
![]() $\mathcal {T}\!\upharpoonright \!\delta $
in
$\mathcal {T}\!\upharpoonright \!\delta $
in
![]() $V[g]$
. By
$V[g]$
. By
![]() $1$
-smallness,
$1$
-smallness,
![]() $Q(b,\mathcal {T}\!\upharpoonright \!\delta )= J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))$
for some
$Q(b,\mathcal {T}\!\upharpoonright \!\delta )= J_{\alpha }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta ))$
for some
![]() $\alpha \in \operatorname {\mathrm {OR}}$
. Since
$\alpha \in \operatorname {\mathrm {OR}}$
. Since
![]() $J_{\beta }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta )) \models "\delta \text { is Woodin}"$
, we must have that
$J_{\beta }(\mathcal {M}(\mathcal {T}\!\upharpoonright \!\delta )) \models "\delta \text { is Woodin}"$
, we must have that
![]() $\beta \leq \alpha $
and
$\beta \leq \alpha $
and
![]() $J_\alpha (\mathcal {M}(\mathcal {T}\!\upharpoonright \! \delta )) \unlhd \mathcal {M}^{\mathcal {T}}_b$
. But since
$J_\alpha (\mathcal {M}(\mathcal {T}\!\upharpoonright \! \delta )) \unlhd \mathcal {M}^{\mathcal {T}}_b$
. But since
![]() $J_\beta (\mathcal {M}(\mathcal {T} \!\upharpoonright \! \delta ))$
satisfies KP + “
$J_\beta (\mathcal {M}(\mathcal {T} \!\upharpoonright \! \delta ))$
satisfies KP + “
![]() $\delta (\mathcal {T})$
is Woodin” and M has no segment modelling this theory, we must have
$\delta (\mathcal {T})$
is Woodin” and M has no segment modelling this theory, we must have
![]() $\beta = \alpha = \operatorname {\mathrm {OR}}(\mathcal {M}^{\mathcal {T}}_b)$
; that is,
$\beta = \alpha = \operatorname {\mathrm {OR}}(\mathcal {M}^{\mathcal {T}}_b)$
; that is,
![]() $J_\beta (\mathcal {M}(\mathcal {T} \!\upharpoonright \! \delta )) = \mathcal {Q}(\mathcal {T} \!\upharpoonright \! \delta ,b) = \mathcal {M}^{\mathcal {T}}_b$
. Since
$J_\beta (\mathcal {M}(\mathcal {T} \!\upharpoonright \! \delta )) = \mathcal {Q}(\mathcal {T} \!\upharpoonright \! \delta ,b) = \mathcal {M}^{\mathcal {T}}_b$
. Since
![]() $M \vert (\xi +\omega )$
satisfies “there is no Woodin cardinal
$M \vert (\xi +\omega )$
satisfies “there is no Woodin cardinal
![]() $\leq \delta $
”, b must drop. But since
$\leq \delta $
”, b must drop. But since
![]() $\mathcal {M}^{\mathcal {T}}_b \models \text {KP} + "\text {there is a Woodin}"$
, by Lemma 15, the last drop in model along b is to a segment modelling this same theory, contradicting the fact that M has no segment modelling this theory.
$\mathcal {M}^{\mathcal {T}}_b \models \text {KP} + "\text {there is a Woodin}"$
, by Lemma 15, the last drop in model along b is to a segment modelling this same theory, contradicting the fact that M has no segment modelling this theory.
The set
![]() $\bar {A}$
gives rise to the set
$\bar {A}$
gives rise to the set
![]() $A=\{\operatorname {\mathrm {OR}}^{\mathcal {M}_{\infty }^{\mathcal {T}}}:\mathcal {T}\in \bar {A}\}$
. Note that A is a set of countable ordinals in
$A=\{\operatorname {\mathrm {OR}}^{\mathcal {M}_{\infty }^{\mathcal {T}}}:\mathcal {T}\in \bar {A}\}$
. Note that A is a set of countable ordinals in
![]() $V[g]$
, since the trees are countable in
$V[g]$
, since the trees are countable in
![]() $V[g]$
and also
$V[g]$
and also
![]() $M\vert \xi +\omega $
is countable in
$M\vert \xi +\omega $
is countable in
![]() $V[g]$
. Thus, we may code A as a set of reals
$V[g]$
. Thus, we may code A as a set of reals
![]() $A^{*}$
by setting
$A^{*}$
by setting
![]() $A^{*}:=\{y \in \text {WO}:\operatorname {\mathrm {otp}}(R_{y})\in A\}$
.
$A^{*}:=\{y \in \text {WO}:\operatorname {\mathrm {otp}}(R_{y})\in A\}$
.
Claim 3.
![]() $A^{*}$
is
$A^{*}$
is
![]() $\Sigma _{1}^{1}(x)$
.
$\Sigma _{1}^{1}(x)$
.
Proof. The main difficulty is in expressing in a
![]() $\Sigma _{1}^{1}(x)$
-fashion that for
$\Sigma _{1}^{1}(x)$
-fashion that for
![]() $\alpha <\delta $
,
$\alpha <\delta $
,
![]() $\mathcal {M}_{\alpha }^{\mathcal {T}}$
is wellfounded. Fix some
$\mathcal {M}_{\alpha }^{\mathcal {T}}$
is wellfounded. Fix some
![]() $\alpha <\delta $
. Note that if
$\alpha <\delta $
. Note that if
![]() $\alpha $
is a successor, then
$\alpha $
is a successor, then
![]() $\mathcal {M}_{\alpha }^{\mathcal {T}}$
is always wellfounded, since M is
$\mathcal {M}_{\alpha }^{\mathcal {T}}$
is always wellfounded, since M is
![]() $(0,\delta +1)$
-iterable in
$(0,\delta +1)$
-iterable in
![]() $V[g]$
as can be seen by standard arguments, and we may assume inductively that
$V[g]$
as can be seen by standard arguments, and we may assume inductively that
![]() $\mathcal {U}\!\upharpoonright \!\alpha $
is guided by Q-structures. Suppose that
$\mathcal {U}\!\upharpoonright \!\alpha $
is guided by Q-structures. Suppose that
![]() $\alpha <\delta $
is a limit. Since
$\alpha <\delta $
is a limit. Since
![]() $\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}}):\alpha <\delta \}=\delta $
, we have that
$\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}}):\alpha <\delta \}=\delta $
, we have that
![]() $\delta (\mathcal {T}\!\upharpoonright \!\alpha )<\delta $
. Note that
$\delta (\mathcal {T}\!\upharpoonright \!\alpha )<\delta $
. Note that
![]() $\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}})>\delta (\mathcal {T}\!\upharpoonright \!\alpha )$
and
$\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}})>\delta (\mathcal {T}\!\upharpoonright \!\alpha )$
and
![]() $\mathcal {M}_{\alpha }^{\mathcal {T}}$
is
$\mathcal {M}_{\alpha }^{\mathcal {T}}$
is
![]() $1$
-small below
$1$
-small below
![]() $\delta $
. Thus,
$\delta $
. Thus,
![]() $Q(b,\mathcal {T}\!\upharpoonright \!\alpha )$
, where
$Q(b,\mathcal {T}\!\upharpoonright \!\alpha )$
, where
![]() $b=[0,\alpha ]^{\mathcal {T}}$
, must exist and
$b=[0,\alpha ]^{\mathcal {T}}$
, must exist and
![]() $Q(b,\mathcal {T}\!\upharpoonright \!\alpha )\lhd \mathcal {M}_{\alpha }^{\mathcal {T}}\vert \operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}})$
. Thus, the wellfoundedness of
$Q(b,\mathcal {T}\!\upharpoonright \!\alpha )\lhd \mathcal {M}_{\alpha }^{\mathcal {T}}\vert \operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {T}})$
. Thus, the wellfoundedness of
![]() $Q(b,\mathcal {T}\!\upharpoonright \!\alpha )$
can be expressed via the existence of an isomorphism between the ordinals of
$Q(b,\mathcal {T}\!\upharpoonright \!\alpha )$
can be expressed via the existence of an isomorphism between the ordinals of
![]() $Q(b,\mathcal {T}\!\upharpoonright \!\alpha )$
and an initial segment of the ordinals of the model coded by x. This is
$Q(b,\mathcal {T}\!\upharpoonright \!\alpha )$
and an initial segment of the ordinals of the model coded by x. This is
![]() $\Sigma _{1}^{1}(x)$
.
$\Sigma _{1}^{1}(x)$
.
Claim 4.
![]() $\sup (A) < \omega _{1}^{\operatorname {\mathrm {CK}}}(x)$
.
$\sup (A) < \omega _{1}^{\operatorname {\mathrm {CK}}}(x)$
.
Proof. This follows immediately from Theorem 23 and the previous claim.
Let
![]() $\mathcal {U}^*$
be the
$\mathcal {U}^*$
be the
![]() $0$
-maximal iteration tree on
$0$
-maximal iteration tree on
![]() $M\vert (\xi +\omega )$
which is otherwise equivalent to
$M\vert (\xi +\omega )$
which is otherwise equivalent to
![]() $\mathcal {U}$
, i.e. it has the same length and tree order, and uses the same extenders as
$\mathcal {U}$
, i.e. it has the same length and tree order, and uses the same extenders as
![]() $\mathcal {U}$
. Since
$\mathcal {U}$
. Since
![]() $\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}}):\alpha <\delta \}=\delta $
and
$\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}}):\alpha <\delta \}=\delta $
and
![]() $\delta $
is a cardinal of M, this makes sense,
$\delta $
is a cardinal of M, this makes sense,
![]() $\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}^*}):\alpha <\delta \}=\delta $
,
$\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}^*}):\alpha <\delta \}=\delta $
,
![]() $i^{\mathcal {U}^*}_{0\delta }$
exists, and
$i^{\mathcal {U}^*}_{0\delta }$
exists, and
![]() $i^{\mathcal {U}^*}_{0\delta }(\delta )=\delta $
. It follows that
$i^{\mathcal {U}^*}_{0\delta }(\delta )=\delta $
. It follows that
![]() $\mathcal {U}^*$
is in
$\mathcal {U}^*$
is in
![]() $\bar {A}$
.
$\bar {A}$
.
The following claim is a simpler version of Lemma 4.64 of [Reference Sargsyan, Schindler and Schlutzenberg7].
Claim 5.
![]() $i_{0\delta }^{\mathcal {U}}(\xi )=i_{0\delta }^{\mathcal {U}^{*}}(\xi )$
.
$i_{0\delta }^{\mathcal {U}}(\xi )=i_{0\delta }^{\mathcal {U}^{*}}(\xi )$
.
Proof. Let
![]() $\kappa < \delta $
. It suffices to see that every function
$\kappa < \delta $
. It suffices to see that every function
![]() $f:\kappa \rightarrow \xi $
which is in M is also in
$f:\kappa \rightarrow \xi $
which is in M is also in
![]() $M\vert \xi +\omega $
. To this end note that since
$M\vert \xi +\omega $
. To this end note that since
![]() $\rho _{\omega }^{M\vert \xi }=\delta $
, there is a surjection
$\rho _{\omega }^{M\vert \xi }=\delta $
, there is a surjection
![]() $g:\delta \rightarrow \xi $
such that
$g:\delta \rightarrow \xi $
such that
![]() $g\in M\vert \xi +\omega =J(M\vert \xi )$
. Define a function
$g\in M\vert \xi +\omega =J(M\vert \xi )$
. Define a function
![]() $h:\kappa \rightarrow \delta $
such that for
$h:\kappa \rightarrow \delta $
such that for
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $h(\alpha )=\min (g^{-1}(f(\alpha )))$
. As
$h(\alpha )=\min (g^{-1}(f(\alpha )))$
. As
![]() $\delta $
is regular and
$\delta $
is regular and
![]() $\kappa <\delta $
, h is essentially a bounded subset of
$\kappa <\delta $
, h is essentially a bounded subset of
![]() $\delta $
and thus,
$\delta $
and thus,
![]() $h\in M\vert \xi $
. But since f is definable from g and h this means that
$h\in M\vert \xi $
. But since f is definable from g and h this means that
![]() $f\in M\vert \xi +\omega $
.
$f\in M\vert \xi +\omega $
.
By Claims 4, 5, and the fact that
![]() $\mathcal {U}^{*}\in \bar {A}$
,
$\mathcal {U}^{*}\in \bar {A}$
,
![]() $i^{\mathcal {U}^*}_{0\delta }(\xi )+\omega = i^{\mathcal {U}}_{0\delta }(\xi )+\omega = \operatorname {\mathrm {OR}}(\mathcal {M}^{\mathcal {U}^*}_\delta )<\omega _1^{\text {CK}(x)}$
. But x is in
$i^{\mathcal {U}^*}_{0\delta }(\xi )+\omega = i^{\mathcal {U}}_{0\delta }(\xi )+\omega = \operatorname {\mathrm {OR}}(\mathcal {M}^{\mathcal {U}^*}_\delta )<\omega _1^{\text {CK}(x)}$
. But x is in
![]() $M[g]$
, so
$M[g]$
, so
![]() $\omega _1^{\text {CK}(x)} < \omega _1^{M[g]} = \delta ^{+M[g]}$
. But we chose
$\omega _1^{\text {CK}(x)} < \omega _1^{M[g]} = \delta ^{+M[g]}$
. But we chose
![]() $\xi $
with
$\xi $
with
![]() $\delta ^{+M[g]}<i^{\mathcal {U}}_{0\delta }(\xi )$
, a contradiction!
$\delta ^{+M[g]}<i^{\mathcal {U}}_{0\delta }(\xi )$
, a contradiction!
We need a second lemma with a similar flavor.
Lemma 25. Let M be a premouse such that
![]() $\delta $
is a regular, uncountable cardinal of M and
$\delta $
is a regular, uncountable cardinal of M and
![]() $M \models "\delta ^{+} \text { exists}"$
. Suppose that M is
$M \models "\delta ^{+} \text { exists}"$
. Suppose that M is
![]() $(0,\delta +1)$
-iterable, and there is no initial segment of M which models KP + “there is a Woodin cardinal”. Let
$(0,\delta +1)$
-iterable, and there is no initial segment of M which models KP + “there is a Woodin cardinal”. Let
![]() $\mathcal {U}$
be a
$\mathcal {U}$
be a
![]() $0$
-maximal iteration tree on M such that
$0$
-maximal iteration tree on M such that
![]() $\operatorname {\mathrm {lh}}(\mathcal {U})=\delta +1$
and
$\operatorname {\mathrm {lh}}(\mathcal {U})=\delta +1$
and
![]() $\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}}):\alpha <\delta \}=\delta $
. Let
$\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}}):\alpha <\delta \}=\delta $
. Let
![]() $b^{\mathcal {U}}:=[0,\delta ]^{\mathcal {U}}$
. Suppose that there is
$b^{\mathcal {U}}:=[0,\delta ]^{\mathcal {U}}$
. Suppose that there is
![]() $\eta \in b^{\mathcal {U}} \cap (\delta \setminus \sup (D^{\mathcal {U}} \cap b^{\mathcal {U}}))$
such that
$\eta \in b^{\mathcal {U}} \cap (\delta \setminus \sup (D^{\mathcal {U}} \cap b^{\mathcal {U}}))$
such that
![]() $i_{\eta \delta }^{\mathcal {U}}(\gamma )=\delta $
for some
$i_{\eta \delta }^{\mathcal {U}}(\gamma )=\delta $
for some
![]() $\gamma <\delta $
. Then
$\gamma <\delta $
. Then
![]() $\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}}<\delta ^{+M}$
.
$\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}}<\delta ^{+M}$
.
Proof. The proof follows closely the proof of Lemma 24. Again we work in
![]() $V[g]$
, where
$V[g]$
, where
![]() $g\subset \operatorname {\mathrm {Col}}(\omega ,\delta )$
is V-generic. We modify the definition of
$g\subset \operatorname {\mathrm {Col}}(\omega ,\delta )$
is V-generic. We modify the definition of
![]() $\bar {A}$
by omitting 2 and modifying 4 to “there exists an
$\bar {A}$
by omitting 2 and modifying 4 to “there exists an
![]() $\eta \in b^{\mathcal {T}} \cap (\delta \setminus \sup (D^{\mathcal {T}} \cap b^{\mathcal {T}}))$
and a
$\eta \in b^{\mathcal {T}} \cap (\delta \setminus \sup (D^{\mathcal {T}} \cap b^{\mathcal {T}}))$
and a
![]() $\gamma <\delta $
such that
$\gamma <\delta $
such that
![]() $i_{\eta \delta }^{\mathcal {T}}(\gamma )=\delta $
, where
$i_{\eta \delta }^{\mathcal {T}}(\gamma )=\delta $
, where
![]() $b^{\mathcal {T}} := [0,\delta ]^{\mathcal {T}}$
”. Moreover, we alter 1 by requiring that
$b^{\mathcal {T}} := [0,\delta ]^{\mathcal {T}}$
”. Moreover, we alter 1 by requiring that
![]() $\mathcal {T}$
is a putative iteration tree on
$\mathcal {T}$
is a putative iteration tree on
![]() $M\vert \delta $
.
$M\vert \delta $
.
As before, for all
![]() $\mathcal {T}\in \bar {A}$
,
$\mathcal {T}\in \bar {A}$
,
![]() $\mathcal {T}$
is an iteration tree. Similar to before
$\mathcal {T}$
is an iteration tree. Similar to before
![]() $\mathcal {U}^{*}$
will be the tree
$\mathcal {U}^{*}$
will be the tree
![]() $\mathcal {U}$
considered on
$\mathcal {U}$
considered on
![]() $M\vert \delta $
. Again,
$M\vert \delta $
. Again,
![]() $\mathcal {U}^{*}\in \bar {A}$
and the tree- and dropping-structure of
$\mathcal {U}^{*}\in \bar {A}$
and the tree- and dropping-structure of
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\mathcal {U}^{*}$
are the same. We have that
$\mathcal {U}^{*}$
are the same. We have that
![]() $\mathcal {M}_{\alpha }^{\mathcal {U}^{*}}\unlhd \mathcal {M}_{\alpha }^{\mathcal {U}}$
for all
$\mathcal {M}_{\alpha }^{\mathcal {U}^{*}}\unlhd \mathcal {M}_{\alpha }^{\mathcal {U}}$
for all
![]() $\alpha \leq \delta $
.
$\alpha \leq \delta $
.
By the same argument as in the proof of Lemma 24, we will have that
![]() $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\delta }^{\mathcal {U}^{*}}}<\omega _{1}^{\operatorname {\mathrm {CK}}}(x)<\delta ^{+M}$
where x codes
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\delta }^{\mathcal {U}^{*}}}<\omega _{1}^{\operatorname {\mathrm {CK}}}(x)<\delta ^{+M}$
where x codes
![]() $M\vert \delta $
. We claim that this implies that
$M\vert \delta $
. We claim that this implies that
![]() $\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}} < \delta ^{+M}$
. If
$\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}} < \delta ^{+M}$
. If
![]() $D^{\mathcal {U}}\cap b^{\mathcal {U}} \neq \emptyset $
, i.e.
$D^{\mathcal {U}}\cap b^{\mathcal {U}} \neq \emptyset $
, i.e.
![]() $\mathcal {U}$
is dropping on its main branch,
$\mathcal {U}$
is dropping on its main branch,
![]() ${\mathcal {M}_{\delta }^{\mathcal {U}}=\mathcal {M}_{\delta }^{\mathcal {U}^{*}}}$
, so that
${\mathcal {M}_{\delta }^{\mathcal {U}}=\mathcal {M}_{\delta }^{\mathcal {U}^{*}}}$
, so that
![]() $\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}}\leq \operatorname {\mathrm {OR}}^{\mathcal {M}_{\delta }^{\mathcal {U}}}<\delta ^{+M}$
. So suppose that
$\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}}\leq \operatorname {\mathrm {OR}}^{\mathcal {M}_{\delta }^{\mathcal {U}}}<\delta ^{+M}$
. So suppose that
![]() $D^{\mathcal {U}}\cap b^{\mathcal {U}}=\emptyset $
, equivalently that
$D^{\mathcal {U}}\cap b^{\mathcal {U}}=\emptyset $
, equivalently that
![]() $D^{\mathcal {U}^{*}}\cap b^{\mathcal {U}}=\emptyset $
. Then
$D^{\mathcal {U}^{*}}\cap b^{\mathcal {U}}=\emptyset $
. Then
![]() $i^{\mathcal {U}}:M\rightarrow \mathcal {M}_{\delta }^{\mathcal {U}}$
and
$i^{\mathcal {U}}:M\rightarrow \mathcal {M}_{\delta }^{\mathcal {U}}$
and
![]() $i^{\mathcal {U}^{*}}:M\vert \delta \rightarrow \mathcal {M}_{\delta }^{\mathcal {U}^{*}}$
exist. Let
$i^{\mathcal {U}^{*}}:M\vert \delta \rightarrow \mathcal {M}_{\delta }^{\mathcal {U}^{*}}$
exist. Let
![]() $\eta <\delta $
be least such that there is
$\eta <\delta $
be least such that there is
![]() $\bar {\delta }<\delta $
such that
$\bar {\delta }<\delta $
such that
![]() $i_{\eta \delta }^{\mathcal {U}^{*}}(\bar {\delta })=\delta $
. If
$i_{\eta \delta }^{\mathcal {U}^{*}}(\bar {\delta })=\delta $
. If
![]() $\eta =0$
, then since
$\eta =0$
, then since
![]() $\delta $
is regular in M and
$\delta $
is regular in M and
![]() $\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}}):\alpha <\delta \}=\delta $
,
$\sup \{\operatorname {\mathrm {lh}}(E_{\alpha }^{\mathcal {U}}):\alpha <\delta \}=\delta $
,
![]() $\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}}=i^{\mathcal {U}}(\bar {\delta }^{+M})\leq i^{\mathcal {U}}(\delta )=\sup i^{\mathcal {U}^{*}}[\delta ]<\omega _{1}^{\operatorname {\mathrm {CK}}}(x)<\delta ^{+M}$
. So suppose that
$\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}}=i^{\mathcal {U}}(\bar {\delta }^{+M})\leq i^{\mathcal {U}}(\delta )=\sup i^{\mathcal {U}^{*}}[\delta ]<\omega _{1}^{\operatorname {\mathrm {CK}}}(x)<\delta ^{+M}$
. So suppose that
![]() $\eta>0$
. Note that
$\eta>0$
. Note that
![]() $\bar {\delta }^{+\mathcal {M}_{\eta }^{\mathcal {U}^{*}}}$
must exist, since otherwise
$\bar {\delta }^{+\mathcal {M}_{\eta }^{\mathcal {U}^{*}}}$
must exist, since otherwise
![]() $\bar {\delta }$
is the largest cardinal of
$\bar {\delta }$
is the largest cardinal of
![]() $\mathcal {M}_{\eta }^{\mathcal {U}^{*}}$
which would imply that
$\mathcal {M}_{\eta }^{\mathcal {U}^{*}}$
which would imply that
![]() $\bar {\delta }\in \operatorname {\mathrm {ran}}(i_{0\eta }^{\mathcal {U}^{*}})$
and so
$\bar {\delta }\in \operatorname {\mathrm {ran}}(i_{0\eta }^{\mathcal {U}^{*}})$
and so
![]() $\eta =0$
, contradicting our assumption on
$\eta =0$
, contradicting our assumption on
![]() $\eta $
. Moreover, since there is no dropping on the main branch,
$\eta $
. Moreover, since there is no dropping on the main branch,
![]() $i_{0\eta }^{\mathcal {U}^{*}}$
is cofinal in
$i_{0\eta }^{\mathcal {U}^{*}}$
is cofinal in
![]() $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\eta }^{\mathcal {U}^{*}}}$
. But then,
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\eta }^{\mathcal {U}^{*}}}$
. But then,
![]() $\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}}=i_{\eta \delta }^{\mathcal {U}}(\bar {\delta }^{+\mathcal {M}_{\eta }^{\mathcal {U}}})=i_{\eta \delta }^{\mathcal {U}^{*}}(\bar {\delta }^{+\mathcal {M}_{\eta }^{\mathcal {U}^{*}}})\leq i_{\eta \delta }^{\mathcal {U}^{*}}(i_{0\eta }^{\mathcal {U}^{*}}(\gamma ))=i^{\mathcal {U}^{*}}(\gamma )<\omega _{1}^{\operatorname {\mathrm {CK}}}(x)$
for some
$\delta ^{+\mathcal {M}_{\delta }^{\mathcal {U}}}=i_{\eta \delta }^{\mathcal {U}}(\bar {\delta }^{+\mathcal {M}_{\eta }^{\mathcal {U}}})=i_{\eta \delta }^{\mathcal {U}^{*}}(\bar {\delta }^{+\mathcal {M}_{\eta }^{\mathcal {U}^{*}}})\leq i_{\eta \delta }^{\mathcal {U}^{*}}(i_{0\eta }^{\mathcal {U}^{*}}(\gamma ))=i^{\mathcal {U}^{*}}(\gamma )<\omega _{1}^{\operatorname {\mathrm {CK}}}(x)$
for some
![]() $\gamma <\delta $
where it is not the case that
$\gamma <\delta $
where it is not the case that
![]() $\delta = \gamma ^{+\mathcal {M}}$
and
$\delta = \gamma ^{+\mathcal {M}}$
and
![]() $i^{\mathcal {U}^*}_{0,\eta }(\gamma ) = \bar {\delta }$
, since
$i^{\mathcal {U}^*}_{0,\eta }(\gamma ) = \bar {\delta }$
, since
![]() $\eta> 0$
.
$\eta> 0$
.
We are now ready to prove the main theorem of this section.
Theorem 26. Let
![]() $\Omega $
be a measurable cardinal. Let
$\Omega $
be a measurable cardinal. Let
![]() $\mathcal {W}$
and
$\mathcal {W}$
and
![]() $\mathcal {R}$
be premice such that
$\mathcal {R}$
be premice such that
![]() $\operatorname {\mathrm {OR}}^{\mathcal {W}}=\operatorname {\mathrm {OR}}^{\mathcal {R}}=\Omega $
and suppose that both are
$\operatorname {\mathrm {OR}}^{\mathcal {W}}=\operatorname {\mathrm {OR}}^{\mathcal {R}}=\Omega $
and suppose that both are
![]() $(0,\Omega +1)$
-iterable. Suppose that neither
$(0,\Omega +1)$
-iterable. Suppose that neither
![]() $\mathcal {W}$
nor
$\mathcal {W}$
nor
![]() $\mathcal {R}$
have an initial segment which models
$\mathcal {R}$
have an initial segment which models
![]() $\text {KP} \land \exists \delta ("\delta \text { is Woodin}")$
. Then the following are equivalent:
$\text {KP} \land \exists \delta ("\delta \text { is Woodin}")$
. Then the following are equivalent:
-
1.
 $\mathcal {W}\leq ^{*}\mathcal {R}$
,
$\mathcal {W}\leq ^{*}\mathcal {R}$
, -
2. there is a club
 $C\subset \Omega $
such that for all
$C\subset \Omega $
such that for all
 $\alpha \in C$
, if
$\alpha \in C$
, if
 $\alpha $
is regular, then
$\alpha $
is regular, then
 $(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
, and
$(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
, and -
3. there is a stationary set
 $S\subset \Omega $
such that for all
$S\subset \Omega $
such that for all
 $\alpha \in S$
,
$\alpha \in S$
,
 $\alpha $
is regular and
$\alpha $
is regular and
 ${(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}}$
.
${(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}}$
.
Proof. Let us first show that clause 1 implies clause 2, i.e. suppose that
![]() $\mathcal {W}\leq ^{*}\mathcal {R}$
. We aim to show that there is a club
$\mathcal {W}\leq ^{*}\mathcal {R}$
. We aim to show that there is a club
![]() $C\subset \Omega $
such that for all
$C\subset \Omega $
such that for all
![]() $\alpha \in C$
, if
$\alpha \in C$
, if
![]() $\alpha $
is regular, then
$\alpha $
is regular, then
![]() $(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
. Let
$(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
. Let
![]() $(\mathcal {T},\mathcal {U})$
be the coiteration of
$(\mathcal {T},\mathcal {U})$
be the coiteration of
![]() $(\mathcal {W},\mathcal {R})$
. By Theorem 21, the coiteration is successful. Since
$(\mathcal {W},\mathcal {R})$
. By Theorem 21, the coiteration is successful. Since
![]() $\mathcal {W}\leq ^{*}\mathcal {R}$
,
$\mathcal {W}\leq ^{*}\mathcal {R}$
,
![]() $\mathcal {M}_{\Omega }^{\mathcal {T}}\unlhd \mathcal {M}_{\Omega }^{\mathcal {U}}$
and
$\mathcal {M}_{\Omega }^{\mathcal {T}}\unlhd \mathcal {M}_{\Omega }^{\mathcal {U}}$
and
![]() $\mathcal {T}$
does not drop on its main branch. In particular,
$\mathcal {T}$
does not drop on its main branch. In particular,
![]() $i^{\mathcal {T}}:\mathcal {W}\rightarrow \mathcal {M}_{\Omega }^{\mathcal {T}}$
exists. We may assume by padding the trees if necessary that
$i^{\mathcal {T}}:\mathcal {W}\rightarrow \mathcal {M}_{\Omega }^{\mathcal {T}}$
exists. We may assume by padding the trees if necessary that
![]() $\operatorname {\mathrm {lh}}(\mathcal {T})=\operatorname {\mathrm {lh}}(\mathcal {U})=\Omega +1$
. Note that by Theorem 21,
$\operatorname {\mathrm {lh}}(\mathcal {T})=\operatorname {\mathrm {lh}}(\mathcal {U})=\Omega +1$
. Note that by Theorem 21,
![]() $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\Omega }^{\mathcal {T}}}=\Omega $
. Thus, by Lemma 22 (1), there is a club
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\Omega }^{\mathcal {T}}}=\Omega $
. Thus, by Lemma 22 (1), there is a club
![]() $C_{\mathcal {T}}\subset \Omega $
such that for all
$C_{\mathcal {T}}\subset \Omega $
such that for all
![]() $\alpha \in C_{\mathcal {T}}$
,
$\alpha \in C_{\mathcal {T}}$
,
![]() $i_{0\alpha }^{\mathcal {T}}[\alpha ]\subset \alpha $
and
$i_{0\alpha }^{\mathcal {T}}[\alpha ]\subset \alpha $
and
![]() $b^{\mathcal {T}} \supset C_{\mathcal {T}}$
. Let
$b^{\mathcal {T}} \supset C_{\mathcal {T}}$
. Let
![]() $\tilde {C}_{\mathcal {T}}$
be the club given by Lemma 22 (2) for
$\tilde {C}_{\mathcal {T}}$
be the club given by Lemma 22 (2) for
![]() $\mathcal {T}$
. Set
$\mathcal {T}$
. Set
![]() $B_{\mathcal {T}}:=C_{\mathcal {T}}\cap \tilde {C}_{\mathcal {T}}$
. Let
$B_{\mathcal {T}}:=C_{\mathcal {T}}\cap \tilde {C}_{\mathcal {T}}$
. Let
![]() $\alpha \in B_{\mathcal {T}}$
and suppose that it is regular. Then
$\alpha \in B_{\mathcal {T}}$
and suppose that it is regular. Then
![]() $i_{0\alpha }^{\mathcal {T}}(\alpha )=\alpha $
. Thus, by Lemma 24, we have that
$i_{0\alpha }^{\mathcal {T}}(\alpha )=\alpha $
. Thus, by Lemma 24, we have that
![]() $\alpha ^{+\mathcal {W}}=\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {T}}}$
. But since
$\alpha ^{+\mathcal {W}}=\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {T}}}$
. But since
![]() $\alpha \in \tilde {C}_{\mathcal {T}}$
,
$\alpha \in \tilde {C}_{\mathcal {T}}$
,
![]() $\operatorname {\mathrm {crit}}(i_{\alpha \Omega }^{\mathcal {T}})\geq \alpha $
. Therefore,
$\operatorname {\mathrm {crit}}(i_{\alpha \Omega }^{\mathcal {T}})\geq \alpha $
. Therefore,
![]() $\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {T}}}=\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}$
. Since
$\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {T}}}=\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}$
. Since
![]() $\mathcal {M}_{\Omega }^{\mathcal {T}}\unlhd \mathcal {M}_{\Omega }^{\mathcal {U}}$
and
$\mathcal {M}_{\Omega }^{\mathcal {T}}\unlhd \mathcal {M}_{\Omega }^{\mathcal {U}}$
and
![]() $\Omega $
is a cardinal, we have that
$\Omega $
is a cardinal, we have that
![]() $\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}=\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}}}$
for all
$\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}=\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}}}$
for all
![]() $\alpha \in B_{\mathcal {T}}$
.
$\alpha \in B_{\mathcal {T}}$
.
Case 1.
 $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\Omega }^{\mathcal {U}}}>\Omega $
.
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\Omega }^{\mathcal {U}}}>\Omega $
.
Let
![]() $C_{\mathcal {U}}\subset \Omega $
be the club given by Lemma 22 (3) for
$C_{\mathcal {U}}\subset \Omega $
be the club given by Lemma 22 (3) for
![]() $\mathcal {U}$
intersected with the club given by Lemma 22 (2) for
$\mathcal {U}$
intersected with the club given by Lemma 22 (2) for
![]() $\mathcal {U}$
. Then for all
$\mathcal {U}$
. Then for all
![]() $\alpha ,\beta \in C_{\mathcal {U}}$
such that
$\alpha ,\beta \in C_{\mathcal {U}}$
such that
![]() $\alpha <\beta $
, we have that
$\alpha <\beta $
, we have that
![]() $i_{\alpha \beta }^{\mathcal {U}}(\alpha )=\beta $
. Suppose that
$i_{\alpha \beta }^{\mathcal {U}}(\alpha )=\beta $
. Suppose that
![]() $\alpha \in C_{\mathcal {U}}^{\prime }$
is regular, where
$\alpha \in C_{\mathcal {U}}^{\prime }$
is regular, where
![]() $C_{\mathcal {U}}^{\prime }$
is the club of limit points of
$C_{\mathcal {U}}^{\prime }$
is the club of limit points of
![]() $C_{\mathcal {U}}$
. We have by Lemma 25, that
$C_{\mathcal {U}}$
. We have by Lemma 25, that
![]() $\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {U}}}<\alpha ^{+\mathcal {R}}$
. Moreover, since
$\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {U}}}<\alpha ^{+\mathcal {R}}$
. Moreover, since
![]() $\operatorname {\mathrm {crit}}(i_{\alpha \Omega }^{\mathcal {U}})= \alpha $
(note we are beyond the drops of
$\operatorname {\mathrm {crit}}(i_{\alpha \Omega }^{\mathcal {U}})= \alpha $
(note we are beyond the drops of
![]() $b^{\mathcal {U}}$
),
$b^{\mathcal {U}}$
),
![]() $\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {U}}}=\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}}}$
. Thus,
$\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {U}}}=\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}}}$
. Thus,
![]() $C:=C_{\mathcal {U}}^{\prime }\cap B_{\mathcal {T}}$
witnesses clause 2 of the theorem in Case 1.
$C:=C_{\mathcal {U}}^{\prime }\cap B_{\mathcal {T}}$
witnesses clause 2 of the theorem in Case 1.
Case 2.
 $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\Omega }^{\mathcal {U}}}=\Omega $
.
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\Omega }^{\mathcal {U}}}=\Omega $
.
Then
![]() $i_{0\Omega }^{\mathcal {U}}$
exists. In this case we can construct a club
$i_{0\Omega }^{\mathcal {U}}$
exists. In this case we can construct a club
![]() $C_{\mathcal {U}}$
for
$C_{\mathcal {U}}$
for
![]() $\mathcal {U}$
as
$\mathcal {U}$
as
![]() $C_{\mathcal {T}}$
was constructed for
$C_{\mathcal {T}}$
was constructed for
![]() $\mathcal {T}$
and set
$\mathcal {T}$
and set
![]() $C:=C_{\mathcal {T}}\cap C_{\mathcal {U}}$
. This C witnesses clause 2 of the theorem in Case 2.
$C:=C_{\mathcal {T}}\cap C_{\mathcal {U}}$
. This C witnesses clause 2 of the theorem in Case 2.
The argument for showing that clause 2 implies clause 3 is standard. We now show that clause 3 implies clause 1. Suppose that there is a stationary set of regular cardinals
![]() $S\subset \Omega $
such that for all
$S\subset \Omega $
such that for all
![]() $\alpha \in S$
,
$\alpha \in S$
,
![]() $\alpha ^{+\mathcal {W}}\leq \alpha ^{+\mathcal {R}}$
. We aim to show that
$\alpha ^{+\mathcal {W}}\leq \alpha ^{+\mathcal {R}}$
. We aim to show that
![]() $\mathcal {W}\leq ^{*}\mathcal {R}$
. Let
$\mathcal {W}\leq ^{*}\mathcal {R}$
. Let
![]() $(\mathcal {T},\mathcal {U})$
be the coiteration of
$(\mathcal {T},\mathcal {U})$
be the coiteration of
![]() $(\mathcal {W},\mathcal {R})$
which again by Theorem 21 is successful. Suppose for the sake of contradiction that
$(\mathcal {W},\mathcal {R})$
which again by Theorem 21 is successful. Suppose for the sake of contradiction that
![]() $\mathcal {M}_{\infty }^{\mathcal {T}}\rhd \mathcal {M}_{\infty }^{\mathcal {U}}$
. By the same arguments as before we can construct a club
$\mathcal {M}_{\infty }^{\mathcal {T}}\rhd \mathcal {M}_{\infty }^{\mathcal {U}}$
. By the same arguments as before we can construct a club
![]() $D\subset \Omega $
such that for all regular
$D\subset \Omega $
such that for all regular
![]() $\alpha \in D$
,
$\alpha \in D$
,
![]() $\alpha ^{+\mathcal {W}}>\alpha ^{+\mathcal {R}}$
. But since S is stationary and consists of regular cardinals,
$\alpha ^{+\mathcal {W}}>\alpha ^{+\mathcal {R}}$
. But since S is stationary and consists of regular cardinals,
![]() $S\cap D\neq \emptyset $
, contradiction!
$S\cap D\neq \emptyset $
, contradiction!
Corollary 27. Let
![]() $\Omega $
be a measurable cardinal. Let
$\Omega $
be a measurable cardinal. Let
![]() $\mathcal {W}$
and
$\mathcal {W}$
and
![]() $\mathcal {R}$
be premice such that
$\mathcal {R}$
be premice such that
![]() $\operatorname {\mathrm {OR}}^{\mathcal {W}}=\operatorname {\mathrm {OR}}^{\mathcal {R}}=\Omega $
and suppose that both are
$\operatorname {\mathrm {OR}}^{\mathcal {W}}=\operatorname {\mathrm {OR}}^{\mathcal {R}}=\Omega $
and suppose that both are
![]() $(0,\Omega +1)$
-iterable. Suppose that there is no transitive model of
$(0,\Omega +1)$
-iterable. Suppose that there is no transitive model of
![]() $\text {KP}\land \exists \delta ("\delta \text { is Woodin}")$
. Then the following are equivalent:
$\text {KP}\land \exists \delta ("\delta \text { is Woodin}")$
. Then the following are equivalent:
-
•
 $\mathcal {W}\leq ^{*}\mathcal {R}$
,
$\mathcal {W}\leq ^{*}\mathcal {R}$
, -
• there is a club
 $C\subset \Omega $
such that for all
$C\subset \Omega $
such that for all
 $\alpha \in C$
, if
$\alpha \in C$
, if
 $\alpha $
is regular, then
$\alpha $
is regular, then
 $(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
, and
$(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
, and -
• there is a stationary set
 $S\subset \Omega $
such that for all
$S\subset \Omega $
such that for all
 $\alpha \in S$
,
$\alpha \in S$
,
 $\alpha \in S$
is regular and
$\alpha \in S$
is regular and
 $(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
.
$(\alpha ^{+})^{\mathcal {W}}\leq (\alpha ^{+})^{\mathcal {R}}$
.
4 The counterexample
In this section we construct a counterexample to Conjecture 1 assuming large cardinals. In order to construct the counterexample we need an iterable premouse M which has an initial segment
![]() $N\lhd M$
such that
$N\lhd M$
such that
![]() $N\models $
KP, N has a largest cardinal
$N\models $
KP, N has a largest cardinal
![]() $\kappa $
which is Woodin in N,
$\kappa $
which is Woodin in N,
![]() $\kappa $
is a measurable cardinal in the larger premouse M, and there exists some
$\kappa $
is a measurable cardinal in the larger premouse M, and there exists some
![]() $\Omega \in (\kappa ^{+M},\operatorname {\mathrm {OR}}^{M})$
which is measurable in M.
$\Omega \in (\kappa ^{+M},\operatorname {\mathrm {OR}}^{M})$
which is measurable in M.
We want to show that such N exists if we assume that M is the least iterable sound premouse, which models
![]() $\text {KP}$
and has a largest cardinal
$\text {KP}$
and has a largest cardinal
![]() $\delta $
which is
$\delta $
which is ![]() -Woodin in M.Footnote
9
-Woodin in M.Footnote
9
In Section 4.1 we will construct the above N. Note that since M is the least mouse with a ![]() -Woodin, we will have that
-Woodin, we will have that
![]() $\kappa $
, the largest cardinal of N, is not
$\kappa $
, the largest cardinal of N, is not ![]() -Woodin in N. For the construction of the counterexample it will be important that if g codes a wellorder and is generic over N for the extender algebra, then the ordertype of g is less than
-Woodin in N. For the construction of the counterexample it will be important that if g codes a wellorder and is generic over N for the extender algebra, then the ordertype of g is less than
![]() $\operatorname {\mathrm {OR}}^N$
. This will work since we showed in Section 2.1 that
$\operatorname {\mathrm {OR}}^N$
. This will work since we showed in Section 2.1 that
![]() $N[g]\models \text {KP}$
if
$N[g]\models \text {KP}$
if
![]() $g\subset \mathbb {P}\in N$
is N-generic,
$g\subset \mathbb {P}\in N$
is N-generic,
![]() $N\models \text {KP}$
, and
$N\models \text {KP}$
, and
![]() $N\models "\mathbb {P}\text { has the }\eta \text {-c.c.}"$
, where
$N\models "\mathbb {P}\text { has the }\eta \text {-c.c.}"$
, where
![]() $\eta $
is the largest cardinal of N. In Section 4.2 we will construct the counterexample.
$\eta $
is the largest cardinal of N. In Section 4.2 we will construct the counterexample.
4.1 The construction of N
Definition 28. Let M be a passive premouse and let
![]() $\delta < \operatorname {\mathrm {OR}} \cap M$
. We say that
$\delta < \operatorname {\mathrm {OR}} \cap M$
. We say that
![]() $\delta $
is a
$\delta $
is a ![]() -Woodin cardinal (of M) if for all
-Woodin cardinal (of M) if for all
![]() $A \in \Sigma _1^M(M)$
there is some
$A \in \Sigma _1^M(M)$
there is some
![]() $\kappa < \delta $
which is
$\kappa < \delta $
which is
![]() $<\delta ,A$
-reflecting in M.
$<\delta ,A$
-reflecting in M.
Definition 29. Let ![]() be the least
be the least
![]() $(0,\omega _{1}+1)$
-iterable and sound premouse which models
$(0,\omega _{1}+1)$
-iterable and sound premouse which models ![]() .
.
Let ![]() . Note that M has a unique Woodin cardinal
. Note that M has a unique Woodin cardinal
![]() $\delta $
. Moreover,
$\delta $
. Moreover,
![]() $\delta $
is acutally
$\delta $
is acutally ![]() -Woodin in M and is the largest cardinal of M. Furthermore,
-Woodin in M and is the largest cardinal of M. Furthermore,
![]() $\delta = \rho ^M_1$
,
$\delta = \rho ^M_1$
,
![]() $p_1^M = \{\delta \}$
, and
$p_1^M = \{\delta \}$
, and
![]() $\rho _2^M = \omega $
. Also, by the remarks in the proof of Lemma 15, M is actually
$\rho _2^M = \omega $
. Also, by the remarks in the proof of Lemma 15, M is actually
![]() $(1,\omega _{1}+1)$
-iterable.
$(1,\omega _{1}+1)$
-iterable.
Definition 30. Let M be an admissible passive premouse such that
![]() $\rho _{1}^{M}<\operatorname {\mathrm {OR}}^{M}$
. We let
$\rho _{1}^{M}<\operatorname {\mathrm {OR}}^{M}$
. We let
![]() $T^{M}\subset \rho _{1}^{M}$
be the set of ordinals coding
$T^{M}\subset \rho _{1}^{M}$
be the set of ordinals coding
![]() $\operatorname {\mathrm {Th}}_{\Sigma _{1}}^{M}(\rho _{1}^{M}\cup \{p_{1}^{M}\})$
.
$\operatorname {\mathrm {Th}}_{\Sigma _{1}}^{M}(\rho _{1}^{M}\cup \{p_{1}^{M}\})$
.
Note that by Lemma 4,
![]() $\rho _{1}^{M}$
is the largest cardinal of M. Moreover, by definition
$\rho _{1}^{M}$
is the largest cardinal of M. Moreover, by definition
![]() $T^{M}\notin M$
, but
$T^{M}\notin M$
, but
![]() $T^{M}\in \Sigma _{1}^{M}(M)$
. However, for every
$T^{M}\in \Sigma _{1}^{M}(M)$
. However, for every
![]() $\alpha <\rho _{1}^{M}$
,
$\alpha <\rho _{1}^{M}$
,
![]() $T^{M}\cap \alpha \in M$
. In the proof of Lemma 31 below, we will consider degree
$T^{M}\cap \alpha \in M$
. In the proof of Lemma 31 below, we will consider degree
![]() $1$
ultrapower embeddings
$1$
ultrapower embeddings
![]() $i_E: M \to U = \text {Ult}_{1}(M,E)$
, where U is wellfounded. Note that in this case,
$i_E: M \to U = \text {Ult}_{1}(M,E)$
, where U is wellfounded. Note that in this case,
![]() ${T^{U} = i_E(T^M)}$
, where
${T^{U} = i_E(T^M)}$
, where
![]() $i_E(T^M)$
denotes
$i_E(T^M)$
denotes
![]() $\bigcup _{\alpha <\rho _1^M} i_E(T^M\cap \alpha )$
.
$\bigcup _{\alpha <\rho _1^M} i_E(T^M\cap \alpha )$
.
Lemma 31. Let
![]() $\delta $
be the largest cardinal of
$\delta $
be the largest cardinal of ![]() . In
. In ![]() , let
, let
![]() $\kappa $
be
$\kappa $
be ![]() -reflecting and let
-reflecting and let
![]() $H:=\text {Hull}_{1}^{M}(\kappa \cup \{\delta \})$
. Then
$H:=\text {Hull}_{1}^{M}(\kappa \cup \{\delta \})$
. Then
-
•
 $H\cap \delta =\kappa $
, and
$H\cap \delta =\kappa $
, and -
• if
 is the transitive collapse of H, then
is the transitive collapse of H, then
 $N\models \text {KP}$
.
$N\models \text {KP}$
.
Proof. Let ![]() . Recall that
. Recall that
![]() $p_1^M = \{\delta \}$
and
$p_1^M = \{\delta \}$
and
![]() $\rho _1^M = \delta $
. Let us first proof that
$\rho _1^M = \delta $
. Let us first proof that
![]() $H\cap \delta =\kappa $
. Suppose for the sake of contradiction that there is
$H\cap \delta =\kappa $
. Suppose for the sake of contradiction that there is
![]() $\xi \in H\cap [\kappa ,\delta )$
. Let
$\xi \in H\cap [\kappa ,\delta )$
. Let
![]() $\varphi _{\xi }$
be a
$\varphi _{\xi }$
be a
![]() $\Sigma _{1}$
formula and
$\Sigma _{1}$
formula and
![]() $\alpha \in \kappa $
be such that
$\alpha \in \kappa $
be such that
![]() $\xi $
is the unique
$\xi $
is the unique
![]() $\eta $
such that
$\eta $
such that
![]() $M\models \varphi _{\xi }(\eta ,\alpha ,p_1^M)$
. Note that
$M\models \varphi _{\xi }(\eta ,\alpha ,p_1^M)$
. Note that
![]() $\varphi _{\xi }(\xi ,\alpha ,p_1^M)\in \operatorname {\mathrm {Th}}_{1}^{M}(\delta \cup \{ {p_1^M} \})$
. Thus, there is some
$\varphi _{\xi }(\xi ,\alpha ,p_1^M)\in \operatorname {\mathrm {Th}}_{1}^{M}(\delta \cup \{ {p_1^M} \})$
. Thus, there is some
![]() $\lambda <\delta $
such that the code for
$\lambda <\delta $
such that the code for
![]() $\varphi _{\xi }(\xi ,\alpha ,p_1^M)$
is below
$\varphi _{\xi }(\xi ,\alpha ,p_1^M)$
is below
![]() $\lambda $
, i.e.
$\lambda $
, i.e.
![]() $\varphi _{\xi }(\xi ,\alpha ,\dot {p})\in T^{M}\cap \lambda $
. Let
$\varphi _{\xi }(\xi ,\alpha ,\dot {p})\in T^{M}\cap \lambda $
. Let
![]() $E\in \mathbb {E}^{M}$
be an extender witnessing that
$E\in \mathbb {E}^{M}$
be an extender witnessing that
![]() $\kappa $
is
$\kappa $
is
![]() $(\lambda ,T^{M})$
-strong. Let
$(\lambda ,T^{M})$
-strong. Let
![]() $U := \text {Ult}_{1}(M,E)$
and let
$U := \text {Ult}_{1}(M,E)$
and let
![]() $i_{E}:M\rightarrow U$
be the canonical ultrapower embedding. Note that we are taking a
$i_{E}:M\rightarrow U$
be the canonical ultrapower embedding. Note that we are taking a
![]() $1$
-ultrapower, which makes sense since
$1$
-ultrapower, which makes sense since
![]() $\kappa = \operatorname {\mathrm {crit}}(E) < \delta = \rho _1^M$
. This means that
$\kappa = \operatorname {\mathrm {crit}}(E) < \delta = \rho _1^M$
. This means that
![]() $i_E(T^M) = T^U$
(see the remarks following Definition 30). But since E is
$i_E(T^M) = T^U$
(see the remarks following Definition 30). But since E is
![]() $(\lambda ,T^{M})$
-strong, we have
$(\lambda ,T^{M})$
-strong, we have
![]() $T^{U}\cap \lambda =i_{E}(T^{M})\cap \lambda =T^{M}\cap \lambda $
. Thus,
$T^{U}\cap \lambda =i_{E}(T^{M})\cap \lambda =T^{M}\cap \lambda $
. Thus,
![]() $\varphi _{\xi }(\xi ,\alpha ,\dot {p})\in T^{U}\cap \lambda $
, which means that
$\varphi _{\xi }(\xi ,\alpha ,\dot {p})\in T^{U}\cap \lambda $
, which means that
![]() $U\models \varphi _{\xi }(\xi ,\alpha ,p_1^{U})$
. Moreover, since
$U\models \varphi _{\xi }(\xi ,\alpha ,p_1^{U})$
. Moreover, since
![]() $M \models \varphi _\xi (\xi , \alpha ,p_1^M)$
,
$M \models \varphi _\xi (\xi , \alpha ,p_1^M)$
,
![]() $U \models \varphi _\xi (i_E(\xi ), i_E(\alpha ), i_E(p_1^M))$
. But
$U \models \varphi _\xi (i_E(\xi ), i_E(\alpha ), i_E(p_1^M))$
. But
![]() $i_E(\alpha ) = \alpha < \kappa $
and
$i_E(\alpha ) = \alpha < \kappa $
and
![]() $i_E(p_1^M) = p_1^U$
,Footnote
10
so
$i_E(p_1^M) = p_1^U$
,Footnote
10
so
![]() ${U \models \varphi _\xi (i_E(\xi ), \alpha , p_1^U)}$
. But since
${U \models \varphi _\xi (i_E(\xi ), \alpha , p_1^U)}$
. But since
![]() $\xi $
was the unique witness for
$\xi $
was the unique witness for
![]() $\exists x\varphi _{\xi }(x,\alpha ,p_1^M)$
in M, we have
$\exists x\varphi _{\xi }(x,\alpha ,p_1^M)$
in M, we have
However, this is
![]() $r\Pi _{1}$
and thus,
$r\Pi _{1}$
and thus,
This means
![]() $i_{E}(\xi )=\xi $
. Contradiction!
$i_{E}(\xi )=\xi $
. Contradiction!
Let us now verify that
![]() $N\models \text {KP}$
. By what we have shown so far
$N\models \text {KP}$
. By what we have shown so far
![]() $\pi (\kappa )=\delta $
. In particular,
$\pi (\kappa )=\delta $
. In particular,
![]() $\kappa $
is the largest cardinal of N. So by Lemma 3 it suffices to check
$\kappa $
is the largest cardinal of N. So by Lemma 3 it suffices to check
![]() $\Delta _{0}$
-collection. Suppose that
$\Delta _{0}$
-collection. Suppose that
where
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Sigma _{1}$
formula and
$\Sigma _{1}$
formula and
![]() $\bar {p}\in N$
. Note that since
$\bar {p}\in N$
. Note that since
![]() $H:=\text {Hull}_{1}^{M}(\kappa \cup \{\delta \})$
, we may replace
$H:=\text {Hull}_{1}^{M}(\kappa \cup \{\delta \})$
, we may replace
![]() $\bar {p}$
with some tuple of ordinals
$\bar {p}$
with some tuple of ordinals
![]() $\vec {\alpha }_p \in [\kappa ]^{<\omega }$
and
$\vec {\alpha }_p \in [\kappa ]^{<\omega }$
and
![]() $\{\kappa \}$
. Letting
$\{\kappa \}$
. Letting
![]() $p=\pi (\bar {p})$
, we have that
$p=\pi (\bar {p})$
, we have that
![]() $p = \vec {\alpha }_p \cup \{ \{ \delta \}\}$
. Then
$p = \vec {\alpha }_p \cup \{ \{ \delta \}\}$
. Then
We aim to see that the bound
![]() $\kappa $
can be replaced by
$\kappa $
can be replaced by
![]() $\delta $
here, giving that
$\delta $
here, giving that
Suppose for the sake of contradiction that there is some
![]() $\xi \in [\kappa ,\delta )$
such that
$\xi \in [\kappa ,\delta )$
such that
![]() ${M\models \forall y\neg \varphi (\xi ,y,\vec {\alpha }_p,\{ \delta \})}$
. This means that
${M\models \forall y\neg \varphi (\xi ,y,\vec {\alpha }_p,\{ \delta \})}$
. This means that
![]() $\exists y\varphi (\xi ,y,\vec {\alpha }_p,\dot {p})\notin T^{M}$
. But then there is some
$\exists y\varphi (\xi ,y,\vec {\alpha }_p,\dot {p})\notin T^{M}$
. But then there is some
![]() $\lambda \in (\xi ,\delta )$
such that this is witnessed by
$\lambda \in (\xi ,\delta )$
such that this is witnessed by
![]() $T^{M}\cap \lambda $
, i.e. the formula
$T^{M}\cap \lambda $
, i.e. the formula
![]() $\exists y\varphi (\xi ,y,\vec {\alpha }_p,\dot {p})\notin T^{M}\cap \lambda $
even though
$\exists y\varphi (\xi ,y,\vec {\alpha }_p,\dot {p})\notin T^{M}\cap \lambda $
even though
![]() $\xi ,\vec {\alpha }_p \in M\vert \lambda $
. (Note that since we coded
$\xi ,\vec {\alpha }_p \in M\vert \lambda $
. (Note that since we coded
![]() $T^{M}$
as a theory with constant symbol
$T^{M}$
as a theory with constant symbol
![]() $\dot {p}$
it suffices if we pick
$\dot {p}$
it suffices if we pick
![]() $\lambda>\sup \{\xi ,\vec {\alpha }_p\}$
.) Let
$\lambda>\sup \{\xi ,\vec {\alpha }_p\}$
.) Let
![]() $E\in \mathbb {E}^{M}$
be
$E\in \mathbb {E}^{M}$
be
![]() $(\lambda ,T^{M})$
-strong. Then as in the previous argument,
$(\lambda ,T^{M})$
-strong. Then as in the previous argument,
![]() $\exists y\varphi (\xi ,y,\vec {\alpha }_p,\dot {p}) \notin T^{U}\cap \lambda $
. However, since
$\exists y\varphi (\xi ,y,\vec {\alpha }_p,\dot {p}) \notin T^{U}\cap \lambda $
. However, since
![]() $i_{E}$
is
$i_{E}$
is
![]() $r\Sigma _{2}$
-elementary, we have that
$r\Sigma _{2}$
-elementary, we have that
Note that
![]() $i_E (\vec {\alpha }_p,\{ \delta \}) = (\vec {\alpha }_p,\{\delta \})$
, since
$i_E (\vec {\alpha }_p,\{ \delta \}) = (\vec {\alpha }_p,\{\delta \})$
, since
![]() $\vec {\alpha }_p \in [\kappa ]^{<\omega }$
and
$\vec {\alpha }_p \in [\kappa ]^{<\omega }$
and
![]() $i_E(\{ \delta \}) = p_1^{U} = p_1^M = \{ \delta \}$
. Thus, since
$i_E(\{ \delta \}) = p_1^{U} = p_1^M = \{ \delta \}$
. Thus, since
![]() $i_{E}(\kappa )>\xi $
,
$i_{E}(\kappa )>\xi $
,
Contradiction!
Lemma 32. Let N be as in Lemma 31. Then
![]() $N\lhd M$
and N is an admissible passive premouse with largest cardinal
$N\lhd M$
and N is an admissible passive premouse with largest cardinal
![]() $\kappa $
which is Woodin in N.
$\kappa $
which is Woodin in N.
Proof. Note that a failure of
![]() $\kappa $
being Woodin in N is an
$\kappa $
being Woodin in N is an
![]() $r\Sigma _{1}$
fact about
$r\Sigma _{1}$
fact about
![]() $N\vert \kappa $
. Since
$N\vert \kappa $
. Since
![]() $H\prec _{\Sigma _{1}}M$
, this would imply by upwards-absoluteness that
$H\prec _{\Sigma _{1}}M$
, this would imply by upwards-absoluteness that
![]() $\delta $
fails to be Woodin in M. Thus,
$\delta $
fails to be Woodin in M. Thus,
![]() $\kappa $
is Woodin in N. Moreover, as already mentioned in the previous proof
$\kappa $
is Woodin in N. Moreover, as already mentioned in the previous proof
![]() $\kappa $
is the largest cardinal of N. But then as
$\kappa $
is the largest cardinal of N. But then as
![]() $N\vert \kappa =M\vert \kappa $
and so
$N\vert \kappa =M\vert \kappa $
and so
![]() $N=J_{\alpha }(M\vert \kappa )$
, we will have that
$N=J_{\alpha }(M\vert \kappa )$
, we will have that
![]() $N\lhd M$
, and we are done.
$N\lhd M$
, and we are done.
4.2 The construction of the counterexample
Let ![]() and let
and let
![]() $N\lhd M$
be as given by Lemma 32, i.e. the following hold:
$N\lhd M$
be as given by Lemma 32, i.e. the following hold:
-
• M has a largest cardinal
 $\delta $
which is
$\delta $
which is  -Woodin in M,
-Woodin in M, -
• N is an admissible mouse with a largest cardinal
 $\kappa $
which is Woodin in N, but not
$\kappa $
which is Woodin in N, but not  -Woodin in N,
-Woodin in N, -
•
 $\operatorname {\mathrm {OR}}^{N}<\kappa ^{+M}$
, and
$\operatorname {\mathrm {OR}}^{N}<\kappa ^{+M}$
, and -
•
 $\kappa $
is measurable in M, as witnessed by an extender E from the extender sequence of M.
$\kappa $
is measurable in M, as witnessed by an extender E from the extender sequence of M.
The construction of the counterexample is now as follows: Fix
![]() $\Omega \in (\kappa ^{++M},\delta )$
, which is a regular cardinal in M. Working inside M we will linearly iterate
$\Omega \in (\kappa ^{++M},\delta )$
, which is a regular cardinal in M. Working inside M we will linearly iterate
![]() $M\vert \operatorname {\mathrm {lh}}(E)$
for
$M\vert \operatorname {\mathrm {lh}}(E)$
for
![]() $\Omega $
many times via E and its images. Let
$\Omega $
many times via E and its images. Let
![]() $\mathcal {T}$
be the corresponding iteration tree on
$\mathcal {T}$
be the corresponding iteration tree on
![]() $M\vert \operatorname {\mathrm {lh}}(E)$
of length
$M\vert \operatorname {\mathrm {lh}}(E)$
of length
![]() $\operatorname {\mathrm {lh}}(\mathcal {T})=\Omega +1$
. Note that
$\operatorname {\mathrm {lh}}(\mathcal {T})=\Omega +1$
. Note that
![]() $\mathcal {T}\in M$
. Let
$\mathcal {T}\in M$
. Let
![]() $i^{\mathcal {T}}:M\vert \operatorname {\mathrm {lh}}(E)\rightarrow \mathcal {M}_{\Omega }^{\mathcal {T}}$
be the iteration map. We will have the following:
$i^{\mathcal {T}}:M\vert \operatorname {\mathrm {lh}}(E)\rightarrow \mathcal {M}_{\Omega }^{\mathcal {T}}$
be the iteration map. We will have the following:
-
•
 $i^{\mathcal {T}}(\kappa )=\Omega $
,
$i^{\mathcal {T}}(\kappa )=\Omega $
, -
•
 $\sup (i^{\mathcal {T}}[\kappa ^{+M}])=i^{\mathcal {T}}(\kappa ^{+M})=\Omega ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}<\Omega ^{+M}$
,
$\sup (i^{\mathcal {T}}[\kappa ^{+M}])=i^{\mathcal {T}}(\kappa ^{+M})=\Omega ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}<\Omega ^{+M}$
, -
•
 $W:=i^{\mathcal {T}}(N)\models \text {KP}$
and
$W:=i^{\mathcal {T}}(N)\models \text {KP}$
and
 $\operatorname {\mathrm {OR}}^{W}<\Omega ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}$
, and
$\operatorname {\mathrm {OR}}^{W}<\Omega ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}$
, and -
• W is an admissible mouse with a largest cardinal
 $\Omega $
which is Woodin in W, but not
$\Omega $
which is Woodin in W, but not  -Woodin in W.
-Woodin in W.
Since
![]() $\Omega ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}<\Omega ^{+M}$
, there is, inside M, some
$\Omega ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}<\Omega ^{+M}$
, there is, inside M, some
![]() $A\subset \Omega $
which codes a well order
$A\subset \Omega $
which codes a well order
![]() $<_A$
such that
$<_A$
such that
![]() $\operatorname {\mathrm {otp}}(<_A)=\Omega ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}$
. Let
$\operatorname {\mathrm {otp}}(<_A)=\Omega ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}$
. Let
![]() $\mathcal {U}$
be the A-genericity iteration of W with respect to the
$\mathcal {U}$
be the A-genericity iteration of W with respect to the
![]() $\Omega $
-generator extender algebra of W at
$\Omega $
-generator extender algebra of W at
![]() $\Omega $
. Note that
$\Omega $
. Note that
![]() $\mathcal {U}\in M$
, since by standard arguments there is for every limit
$\mathcal {U}\in M$
, since by standard arguments there is for every limit
![]() $\alpha \leq \Omega $
a Q-structure for
$\alpha \leq \Omega $
a Q-structure for
![]() $\mathcal {U}\!\upharpoonright \!\alpha $
in M. Moreover, since
$\mathcal {U}\!\upharpoonright \!\alpha $
in M. Moreover, since
![]() $\Omega $
is inaccessible in W, and a cardinal in M, by the usual arguments
$\Omega $
is inaccessible in W, and a cardinal in M, by the usual arguments
![]() $\mathcal {U}$
is non-dropping,
$\mathcal {U}$
is non-dropping,
![]() $\operatorname {\mathrm {lh}}(\mathcal {U})=\Omega +1$
, and
$\operatorname {\mathrm {lh}}(\mathcal {U})=\Omega +1$
, and
![]() $i_{0\Omega }^{\mathcal {U}}(\Omega )=\Omega $
.
$i_{0\Omega }^{\mathcal {U}}(\Omega )=\Omega $
.
Inside M we construct a club
![]() $C\subset \Omega $
such that for all
$C\subset \Omega $
such that for all
![]() $\alpha \in C$
:
$\alpha \in C$
:
-
• there exists some
 $\pi _{\alpha }:M_{\alpha }\cong X_{\alpha }\prec _{1000}M\vert \vert \Omega ^{++}$
such that
$\pi _{\alpha }:M_{\alpha }\cong X_{\alpha }\prec _{1000}M\vert \vert \Omega ^{++}$
such that
 $M\vert (\operatorname {\mathrm {lh}}(E)+\omega ) \cup \{\Omega ,A\}\subset \operatorname {\mathrm {ran}}(\pi _{\alpha })$
,
$M\vert (\operatorname {\mathrm {lh}}(E)+\omega ) \cup \{\Omega ,A\}\subset \operatorname {\mathrm {ran}}(\pi _{\alpha })$
,
 $\operatorname {\mathrm {crit}}(\pi _{\alpha })=\alpha $
, and
$\operatorname {\mathrm {crit}}(\pi _{\alpha })=\alpha $
, and
 $\pi _{\alpha }(\alpha )=\Omega $
,
$\pi _{\alpha }(\alpha )=\Omega $
, -
•
 $\alpha =\sup \{\operatorname {\mathrm {lh}}(E_{\beta }^{\mathcal {U}}):\beta <\alpha \}$
,
$\alpha =\sup \{\operatorname {\mathrm {lh}}(E_{\beta }^{\mathcal {U}}):\beta <\alpha \}$
, -
•
 $\alpha \in b:=[0,\Omega ]^{\mathcal {U}}$
, and
$\alpha \in b:=[0,\Omega ]^{\mathcal {U}}$
, and -
•
 $\alpha =\operatorname {\mathrm {crit}}(E_{\alpha }^{\mathcal {T}})$
.
$\alpha =\operatorname {\mathrm {crit}}(E_{\alpha }^{\mathcal {T}})$
.
The construction of such C is fairly standard, so we will omit it. Note that for
![]() $\alpha \in C$
,
$\alpha \in C$
,
![]() $\operatorname {\mathrm {crit}}(i_{\alpha \Omega }^{\mathcal {U}})\geq \alpha $
, since
$\operatorname {\mathrm {crit}}(i_{\alpha \Omega }^{\mathcal {U}})\geq \alpha $
, since
![]() $\alpha =\sup \{\operatorname {\mathrm {lh}}(E_{\beta }^{\mathcal {U}}):\beta <\alpha \}$
. Thus, by the usual argument
$\alpha =\sup \{\operatorname {\mathrm {lh}}(E_{\beta }^{\mathcal {U}}):\beta <\alpha \}$
. Thus, by the usual argument
![]() $\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {U}}}=\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}}}$
.
$\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {U}}}=\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}}}$
.
Claim. For
![]() $\alpha \in C$
,
$\alpha \in C$
,
![]() $\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {U}}}>\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}$
.
$\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {U}}}>\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}$
.
Proof. Fix
![]() $\alpha \in C$
. Let
$\alpha \in C$
. Let
![]() $(\bar {\mathcal {T}},\bar {\mathcal {U}},\bar {A},\bar {W})\in M_{\alpha }$
such that
$(\bar {\mathcal {T}},\bar {\mathcal {U}},\bar {A},\bar {W})\in M_{\alpha }$
such that
![]() $\pi _{\alpha }((\bar {\mathcal {T}},\bar {\mathcal {U}},\bar {A},\bar {W}))=(\mathcal {T},\mathcal {U},A,W)$
. Note that there are such
$\pi _{\alpha }((\bar {\mathcal {T}},\bar {\mathcal {U}},\bar {A},\bar {W}))=(\mathcal {T},\mathcal {U},A,W)$
. Note that there are such
![]() $\bar {\mathcal {T}},\bar {\mathcal {U}},\bar {W}\in M_{\alpha }$
, since
$\bar {\mathcal {T}},\bar {\mathcal {U}},\bar {W}\in M_{\alpha }$
, since
![]() $\mathcal {T},\mathcal {U},W$
are definable from
$\mathcal {T},\mathcal {U},W$
are definable from
![]() $M\vert \operatorname {\mathrm {lh}}(E)$
, A, and
$M\vert \operatorname {\mathrm {lh}}(E)$
, A, and
![]() $\Omega $
over
$\Omega $
over
![]() $M \vert \vert \Omega ^{++}$
.
$M \vert \vert \Omega ^{++}$
.
By the properties of
![]() $\pi _\alpha $
,
$\pi _\alpha $
,
![]() $\bar {A}$
is generic over
$\bar {A}$
is generic over
![]() $\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}$
and
$\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}$
and
![]() $\operatorname {\mathrm {otp}}(<_{\bar {A}}) = \alpha ^{+\mathcal {M}^{\bar {\mathcal {T}}}_\alpha } = \alpha ^{+\mathcal {M}^{\mathcal {T}}_\alpha }$
. By Corollary 11,
$\operatorname {\mathrm {otp}}(<_{\bar {A}}) = \alpha ^{+\mathcal {M}^{\bar {\mathcal {T}}}_\alpha } = \alpha ^{+\mathcal {M}^{\mathcal {T}}_\alpha }$
. By Corollary 11,
![]() $\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}[\bar {A}]\models \text {KP}$
. Since
$\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}[\bar {A}]\models \text {KP}$
. Since
![]() ${<_{\bar {A}}} \in {\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}[\bar {A}]}$
and the transitive collapse of
${<_{\bar {A}}} \in {\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}[\bar {A}]}$
and the transitive collapse of
![]() $<_{\bar {A}}$
is a
$<_{\bar {A}}$
is a
![]() $\Sigma _{1}$
-recursion,
$\Sigma _{1}$
-recursion,
![]() $\operatorname {\mathrm {otp}}(<_{\bar {A}})=\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {T}}}\in \mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}[\bar {A}]$
. In particular,
$\operatorname {\mathrm {otp}}(<_{\bar {A}})=\alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {T}}}\in \mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}[\bar {A}]$
. In particular,
![]() $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}[\bar {A}]} = \operatorname {\mathrm {OR}}^{\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}}> \alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {T}}}$
. Note that since
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}[\bar {A}]} = \operatorname {\mathrm {OR}}^{\mathcal {M}_{\alpha }^{\bar {\mathcal {U}}}}> \alpha ^{+\mathcal {M}_{\alpha }^{\mathcal {T}}}$
. Note that since
![]() $\operatorname {\mathrm {crit}}(E^{\mathcal {T}}_\alpha ) = \alpha $
it follows by the usual argument that
$\operatorname {\mathrm {crit}}(E^{\mathcal {T}}_\alpha ) = \alpha $
it follows by the usual argument that
![]() $\alpha ^{+\mathcal {M}^{\mathcal {T}}_\alpha } = \alpha ^{+\mathcal {M}^{\mathcal {T}}_\Omega }$
. So in order to finish the proof it suffices to see that
$\alpha ^{+\mathcal {M}^{\mathcal {T}}_\alpha } = \alpha ^{+\mathcal {M}^{\mathcal {T}}_\Omega }$
. So in order to finish the proof it suffices to see that
![]() $\operatorname {\mathrm {OR}}^{\mathcal {M}^{\bar {\mathcal {U}}}_\alpha } \leq \alpha ^{+\mathcal {M}^{\mathcal {U}}_\alpha }$
.
$\operatorname {\mathrm {OR}}^{\mathcal {M}^{\bar {\mathcal {U}}}_\alpha } \leq \alpha ^{+\mathcal {M}^{\mathcal {U}}_\alpha }$
.
Since
![]() $\operatorname {\mathrm {crit}}(\pi _\alpha ) = \alpha $
, we have that
$\operatorname {\mathrm {crit}}(\pi _\alpha ) = \alpha $
, we have that
![]() $\mathcal {M}_\alpha ^{\bar {\mathcal {U}}} \vert \alpha = \mathcal {M}_\alpha ^{\mathcal {U}} \vert \alpha $
. Moreover, since
$\mathcal {M}_\alpha ^{\bar {\mathcal {U}}} \vert \alpha = \mathcal {M}_\alpha ^{\mathcal {U}} \vert \alpha $
. Moreover, since
![]() $i^{\mathcal {U}}_{0,\Omega } (\Omega ) = \Omega $
,
$i^{\mathcal {U}}_{0,\Omega } (\Omega ) = \Omega $
,
![]() $i^{\bar {\mathcal {U}}}_{0\alpha }(\alpha ) = \alpha $
and so
$i^{\bar {\mathcal {U}}}_{0\alpha }(\alpha ) = \alpha $
and so
![]() $\mathcal {M}^{\bar {\mathcal {U}}}_\alpha \models "\alpha \text { is Woodin}"$
, since
$\mathcal {M}^{\bar {\mathcal {U}}}_\alpha \models "\alpha \text { is Woodin}"$
, since
![]() $\pi _\alpha (\mathcal {M}^{\bar {\mathcal {U}}}_\alpha ) = \mathcal {M}^{\mathcal {U}}_\Omega $
and
$\pi _\alpha (\mathcal {M}^{\bar {\mathcal {U}}}_\alpha ) = \mathcal {M}^{\mathcal {U}}_\Omega $
and
![]() $\mathcal {M}^{\mathcal {U}}_\Omega \models "\Omega \text { is Woodin}"$
. By the
$\mathcal {M}^{\mathcal {U}}_\Omega \models "\Omega \text { is Woodin}"$
. By the
![]() $1$
-smallness of
$1$
-smallness of
![]() $\mathcal {M}_\Omega ^{\mathcal {U}}$
it follows that
$\mathcal {M}_\Omega ^{\mathcal {U}}$
it follows that
![]() $\mathcal {M}^{\bar {\mathcal {U}}}_\alpha = J_\beta (\mathcal {M}^{\bar {\mathcal {U}}}_\alpha \vert \alpha )$
for some
$\mathcal {M}^{\bar {\mathcal {U}}}_\alpha = J_\beta (\mathcal {M}^{\bar {\mathcal {U}}}_\alpha \vert \alpha )$
for some
![]() $\beta < \Omega $
and so
$\beta < \Omega $
and so
![]() $\mathcal {M}^{\bar {\mathcal {U}}}_\alpha \unlhd \mathcal {Q}(\mathcal {U} \!\upharpoonright \! \alpha )$
, so that
$\mathcal {M}^{\bar {\mathcal {U}}}_\alpha \unlhd \mathcal {Q}(\mathcal {U} \!\upharpoonright \! \alpha )$
, so that
![]() $\mathcal {M}^{\bar {\mathcal {U}}}_\alpha \lhd \mathcal {M}_\Omega ^{\mathcal {U}}$
. Since
$\mathcal {M}^{\bar {\mathcal {U}}}_\alpha \lhd \mathcal {M}_\Omega ^{\mathcal {U}}$
. Since
![]() $\mathcal {Q}(\mathcal {U} \!\upharpoonright \! \alpha ) \unlhd \mathcal {M}_\Omega ^{\mathcal {U}} \vert \alpha ^{+\mathcal {M}_\Omega ^{\mathcal {U}}}$
, we have
$\mathcal {Q}(\mathcal {U} \!\upharpoonright \! \alpha ) \unlhd \mathcal {M}_\Omega ^{\mathcal {U}} \vert \alpha ^{+\mathcal {M}_\Omega ^{\mathcal {U}}}$
, we have
![]() $\operatorname {\mathrm {OR}}^{\mathcal {M}^{\bar {\mathcal {U}}}_\alpha } \leq \alpha ^{+\mathcal {M}^{\mathcal {U}}_\alpha }$
.
$\operatorname {\mathrm {OR}}^{\mathcal {M}^{\bar {\mathcal {U}}}_\alpha } \leq \alpha ^{+\mathcal {M}^{\mathcal {U}}_\alpha }$
.
We have shown that for every
![]() $\alpha \in C$
,
$\alpha \in C$
,
![]() $\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}<\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}}}$
. If we consider the tree
$\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {T}}}<\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}}}$
. If we consider the tree
![]() $\mathcal {U}^{*}$
which is just the tree
$\mathcal {U}^{*}$
which is just the tree
![]() $\mathcal {U}$
considered not on W but on
$\mathcal {U}$
considered not on W but on
![]() $W\vert \Omega $
, we will have that for all
$W\vert \Omega $
, we will have that for all
![]() $\alpha \in C$
,
$\alpha \in C$
,
![]() $\alpha ^{+W\vert \Omega }<\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}}$
. Moreover, since
$\alpha ^{+W\vert \Omega }<\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}}$
. Moreover, since
![]() $i^{\mathcal {U}}(\Omega )=\Omega $
, we have
$i^{\mathcal {U}}(\Omega )=\Omega $
, we have
![]() $\operatorname {\mathrm {OR}}^{\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}}=\Omega $
, so
$\operatorname {\mathrm {OR}}^{\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}}=\Omega $
, so
![]() $\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}$
is a weasel in the sense of M.
$\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}$
is a weasel in the sense of M.
However, if
![]() $(\mathcal {T}^{\prime },\mathcal {U}^{\prime })$
is the coiteration of
$(\mathcal {T}^{\prime },\mathcal {U}^{\prime })$
is the coiteration of
![]() $(W\vert \Omega ,\mathcal {M}_{\Omega }^{\mathcal {U}^{*}})$
, then
$(W\vert \Omega ,\mathcal {M}_{\Omega }^{\mathcal {U}^{*}})$
, then
![]() $\mathcal {T}^{\prime }=\mathcal {U}^{*}$
and
$\mathcal {T}^{\prime }=\mathcal {U}^{*}$
and
![]() $\mathcal {U}^{\prime }$
is the trivial tree. Thus,
$\mathcal {U}^{\prime }$
is the trivial tree. Thus,
![]() $W\vert \Omega =^{*}\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}$
and there exists a club
$W\vert \Omega =^{*}\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}$
and there exists a club
![]() $C\subset \Omega $
such that for all
$C\subset \Omega $
such that for all
![]() $\alpha \in C$
,
$\alpha \in C$
,
![]() $\alpha ^{+W\vert \Omega }<\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}}$
. This contradicts Conjecture 1 inside M.
$\alpha ^{+W\vert \Omega }<\alpha ^{+\mathcal {M}_{\Omega }^{\mathcal {U}^{*}}}$
. This contradicts Conjecture 1 inside M.
Remark. The construction above also works if we picked
![]() $\Omega $
to be
$\Omega $
to be
![]() $\delta $
. However, in this case, we have to modify the construction slightly: Let
$\delta $
. However, in this case, we have to modify the construction slightly: Let
![]() $\eta>\kappa $
be a measurable cardinal of M and let
$\eta>\kappa $
be a measurable cardinal of M and let
![]() $F\in \mathbb {E}^{M}$
be the measure witnessing this. Let
$F\in \mathbb {E}^{M}$
be the measure witnessing this. Let
![]() $\mathcal {T}^{\prime }$
the linear iteration of
$\mathcal {T}^{\prime }$
the linear iteration of
![]() $M\vert \eta ^{++M}$
via F and its images of length
$M\vert \eta ^{++M}$
via F and its images of length
![]() $\delta +1$
. Note that by
$\delta +1$
. Note that by
![]() $\Delta _{0}$
-collection
$\Delta _{0}$
-collection
![]() $\mathcal {T}^{\prime }\in M$
and that
$\mathcal {T}^{\prime }\in M$
and that
![]() $\delta ^{+}$
exists in
$\delta ^{+}$
exists in
![]() $\mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}$
. Now as before we let
$\mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}$
. Now as before we let
![]() $\mathcal {T}$
be a linear iteration of
$\mathcal {T}$
be a linear iteration of
![]() $M\vert \operatorname {\mathrm {lh}}(E)$
via E and its images of length
$M\vert \operatorname {\mathrm {lh}}(E)$
via E and its images of length
![]() $\delta +1$
. However, note that
$\delta +1$
. However, note that
![]() $\mathcal {T}\in \mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}$
. Thus, there is
$\mathcal {T}\in \mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}$
. Thus, there is
![]() $A\in \mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}$
such that
$A\in \mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}$
such that
![]() $\operatorname {\mathrm {otp}}(<_A)=\delta ^{+\mathcal {M}_{\delta }^{\mathcal {T}}}$
and
$\operatorname {\mathrm {otp}}(<_A)=\delta ^{+\mathcal {M}_{\delta }^{\mathcal {T}}}$
and
![]() $A\subset \delta $
. Since
$A\subset \delta $
. Since
![]() $\delta ^{+\mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}}$
exists and there is no initial segment of
$\delta ^{+\mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}}$
exists and there is no initial segment of
![]() $\mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}$
which models KP and has a
$\mathcal {M}_{\delta }^{\mathcal {T}^{\prime }}$
which models KP and has a ![]() -Woodin cardinal, we see by the same argument as before, that Q-structures exist for
-Woodin cardinal, we see by the same argument as before, that Q-structures exist for
![]() $\mathcal {U}$
, where
$\mathcal {U}$
, where
![]() $\mathcal {U}$
is the genericity iteration of
$\mathcal {U}$
is the genericity iteration of
![]() $i_{0\delta }^{\mathcal {T}}(N)$
making A generic.
$i_{0\delta }^{\mathcal {T}}(N)$
making A generic.
5 On another question from CMIP
In this last section we discuss another question remarked about in [Reference Steel10, prior to Lemma 4.6] concerning the S-hull property. Throughout this section
![]() $\Omega $
is a fixed measurable cardinal and
$\Omega $
is a fixed measurable cardinal and
![]() $\mu _{0}$
is a fixed normal measure on
$\mu _{0}$
is a fixed normal measure on
![]() $\Omega $
. We call a premouse of ordinal height
$\Omega $
. We call a premouse of ordinal height
![]() $\Omega $
a weasel.
$\Omega $
a weasel.
Note that our definitions of thickness and the Hull property are different from the ones in [Reference Steel10], yet equivalent. We chose these different definitions in order to emphasize that thickness is a property independent of a specific weasel.
Definition 33. Let
![]() $\mathcal {W}$
be a weasel and
$\mathcal {W}$
be a weasel and
![]() $S\subset \Omega $
be stationary. We say that S is good for
$S\subset \Omega $
be stationary. We say that S is good for
![]() $\mathcal {W}$
iff there is a club
$\mathcal {W}$
iff there is a club
![]() $C\subset \Omega $
such that for all
$C\subset \Omega $
such that for all
![]() $\alpha \in C\cap S$
$\alpha \in C\cap S$
-
•
 $\alpha $
is inaccessible,
$\alpha $
is inaccessible, -
•
 $\alpha ^{+}=(\alpha ^{+})^{\mathcal {W}}$
, and
$\alpha ^{+}=(\alpha ^{+})^{\mathcal {W}}$
, and -
•
 $\alpha $
is not the critical point of a total-on-
$\alpha $
is not the critical point of a total-on-
 $\mathcal {W}$
extender from the extender sequence of
$\mathcal {W}$
extender from the extender sequence of
 $\mathcal {W}$
.
$\mathcal {W}$
.
Definition 34. Let
![]() $\Gamma \subset \Omega $
and S be stationary. We say that
$\Gamma \subset \Omega $
and S be stationary. We say that
![]() $\Gamma $
is S-thick iff there is a club
$\Gamma $
is S-thick iff there is a club
![]() $C\subset \Omega $
such that for all
$C\subset \Omega $
such that for all
![]() $\alpha \in C\cap S$
,
$\alpha \in C\cap S$
,
![]() $\Gamma \cap \alpha ^{+}$
contains an
$\Gamma \cap \alpha ^{+}$
contains an
![]() $\alpha $
-club and
$\alpha $
-club and
![]() $\alpha \in \Gamma $
.
$\alpha \in \Gamma $
.
Definition 35. Let
![]() $\mathcal {W}$
be a weasel and
$\mathcal {W}$
be a weasel and
![]() $S\subset \Omega $
such that S is good for
$S\subset \Omega $
such that S is good for
![]() $\mathcal {W}$
. Let
$\mathcal {W}$
. Let
![]() $\alpha < \Omega $
. We say that
$\alpha < \Omega $
. We say that
![]() $\mathcal {W}$
has the S-hull property at
$\mathcal {W}$
has the S-hull property at
![]() $\alpha $
iff for all
$\alpha $
iff for all
![]() $\Gamma \subset \Omega $
which are S-thick
$\Gamma \subset \Omega $
which are S-thick
In Lemma 4.6 of [Reference Steel10, p. 32] it is proven that for an
![]() $\Omega +1$
-iterable weasel
$\Omega +1$
-iterable weasel
![]() $\mathcal {W}$
, if S is good for
$\mathcal {W}$
, if S is good for
![]() $\mathcal {W}$
, then for
$\mathcal {W}$
, then for
![]() $\mu _{0}$
-a.e.
$\mu _{0}$
-a.e.
![]() $\alpha <\Omega $
the S-hull property holds at
$\alpha <\Omega $
the S-hull property holds at
![]() $\alpha $
.
$\alpha $
.
However, in [Reference Steel10, p. 32, prior to Lemma 4.6], Steel raises the issue whether the set
![]() $\operatorname {\mathrm {HP}}_S^{\mathcal {W}}:=\{\alpha <\Omega :\mathcal {W}\text { has the }S\text {-hull property at }\alpha \}$
is closed. Note that
$\operatorname {\mathrm {HP}}_S^{\mathcal {W}}:=\{\alpha <\Omega :\mathcal {W}\text { has the }S\text {-hull property at }\alpha \}$
is closed. Note that
![]() $\operatorname {\mathrm {HP}}_S^{\mathcal {W}}$
clearly cannot be closed in the usual sense, as the following example from [Reference Steel10, p. 29] shows: Suppose that M is an
$\operatorname {\mathrm {HP}}_S^{\mathcal {W}}$
clearly cannot be closed in the usual sense, as the following example from [Reference Steel10, p. 29] shows: Suppose that M is an
![]() $\Omega +1$
-iterable weasel which has the S-hull property at all
$\Omega +1$
-iterable weasel which has the S-hull property at all
![]() $\alpha <\Omega $
and there is a total-on-
$\alpha <\Omega $
and there is a total-on-
![]() $M E\in \mathbb {E}^{M}$
with at least two generators. Then
$M E\in \mathbb {E}^{M}$
with at least two generators. Then
![]() $\text {Ult}_{0}(M,E)$
has the S-hull property at all
$\text {Ult}_{0}(M,E)$
has the S-hull property at all
![]() $\alpha <(\operatorname {\mathrm {crit}}(E)^{+})^{M}$
but not at
$\alpha <(\operatorname {\mathrm {crit}}(E)^{+})^{M}$
but not at
![]() $(\operatorname {\mathrm {crit}}(E)^{+})^{M}$
. However,
$(\operatorname {\mathrm {crit}}(E)^{+})^{M}$
. However,
![]() $\text {Ult}_{0}(M,E)$
is still
$\text {Ult}_{0}(M,E)$
is still
![]() $\Omega +1$
-iterable. Thus,
$\Omega +1$
-iterable. Thus,
![]() $\operatorname {\mathrm {HP}}_S^{\mathcal {W}}$
cannot be closed in the usual sense.
$\operatorname {\mathrm {HP}}_S^{\mathcal {W}}$
cannot be closed in the usual sense.
Definition 36. We say that
![]() $X\subset \Omega $
is almost closed if for every
$X\subset \Omega $
is almost closed if for every
![]() $\delta < \Omega $
, if
$\delta < \Omega $
, if
![]() $\delta $
is the supremum of elements of X and elements of
$\delta $
is the supremum of elements of X and elements of
![]() $\Omega \setminus X$
, then
$\Omega \setminus X$
, then
![]() $\delta \in X$
.
$\delta \in X$
.
Given the preceding remarks, we will substitute almost closure for closure in the issue raised in [Reference Steel10], and hence consider the following question: Let
![]() $\mathcal {W}$
be a
$\mathcal {W}$
be a
![]() $(0,\Omega +1)$
-iterable weasel and
$(0,\Omega +1)$
-iterable weasel and
![]() $S \subset \Omega $
such that S is good for
$S \subset \Omega $
such that S is good for
![]() $\mathcal {W}$
, is the set
$\mathcal {W}$
, is the set
![]() $\operatorname {\mathrm {HP}}_S^{\mathcal {W}}$
almost closed?
$\operatorname {\mathrm {HP}}_S^{\mathcal {W}}$
almost closed?
This question is answered positively by the following theorem.
Theorem 37. Let
![]() $\mathcal {W}$
be an
$\mathcal {W}$
be an
![]() $\Omega +1$
-iterable weasel and
$\Omega +1$
-iterable weasel and
![]() $S\subset \Omega $
be such that S is good for
$S\subset \Omega $
be such that S is good for
![]() $\mathcal {W}$
. Then the set
$\mathcal {W}$
. Then the set
![]() $\{\alpha <\Omega :\mathcal {W}\text { has the }S\text {-hull property at }\alpha \}$
is almost closed.
$\{\alpha <\Omega :\mathcal {W}\text { has the }S\text {-hull property at }\alpha \}$
is almost closed.
Proof. By Lemma 4.5 of [Reference Steel10] there is an
![]() $\Omega +1$
-iterable weasel M and an elementary embedding
$\Omega +1$
-iterable weasel M and an elementary embedding
![]() $\pi :M\rightarrow \mathcal {W}$
such that
$\pi :M\rightarrow \mathcal {W}$
such that
![]() $\operatorname {\mathrm {ran}}(\pi )$
is S-thick and M has the S-hull property at all
$\operatorname {\mathrm {ran}}(\pi )$
is S-thick and M has the S-hull property at all
![]() $\alpha <\Omega $
, i.e.
$\alpha <\Omega $
, i.e.
![]() $\operatorname {\mathrm {HP}}_S^{M}=\Omega $
. Let
$\operatorname {\mathrm {HP}}_S^{M}=\Omega $
. Let
![]() $(\mathcal {T},\mathcal {U})$
be the coiteration of
$(\mathcal {T},\mathcal {U})$
be the coiteration of
![]() $\mathcal {W}$
and M. We will prove the theorem assuming that
$\mathcal {W}$
and M. We will prove the theorem assuming that
![]() $\operatorname {\mathrm {lh}}(\mathcal {T})=\operatorname {\mathrm {lh}}(\mathcal {U})=\Omega +1$
and leave the remaining cases as an exercise to the reader. Since
$\operatorname {\mathrm {lh}}(\mathcal {T})=\operatorname {\mathrm {lh}}(\mathcal {U})=\Omega +1$
and leave the remaining cases as an exercise to the reader. Since
![]() $\mathcal {W}$
and M are universal,
$\mathcal {W}$
and M are universal,
![]() $i^{\mathcal {T}}:\mathcal {W}\rightarrow \mathcal {M}_{\Omega }^{\mathcal {T}}$
and
$i^{\mathcal {T}}:\mathcal {W}\rightarrow \mathcal {M}_{\Omega }^{\mathcal {T}}$
and
![]() $i^{\mathcal {U}}:M\rightarrow \mathcal {M}_{\Omega }^{\mathcal {U}}$
exist and
$i^{\mathcal {U}}:M\rightarrow \mathcal {M}_{\Omega }^{\mathcal {U}}$
exist and
![]() $\mathcal {M}_{\Omega }^{\mathcal {T}}=\mathcal {M}_{\Omega }^{\mathcal {U}}=:M_{\infty }$
.
$\mathcal {M}_{\Omega }^{\mathcal {T}}=\mathcal {M}_{\Omega }^{\mathcal {U}}=:M_{\infty }$
.
Note that by the remark following Example 4.3 in [Reference Steel10, p. 29],
![]() $M_{\infty }$
has the S-hull property at
$M_{\infty }$
has the S-hull property at
![]() $\xi $
iff for no
$\xi $
iff for no
![]() $\beta +1\in [0,\Omega ]^{\mathcal {U}}$
,
$\beta +1\in [0,\Omega ]^{\mathcal {U}}$
,
![]() $\xi \in [\operatorname {\mathrm {crit}}(E_{\beta }^{\mathcal {U}})^{+\mathcal {M}_{\eta }^{\mathcal {U}}},\nu (E_{\beta }^{\mathcal {U}}))$
, where
$\xi \in [\operatorname {\mathrm {crit}}(E_{\beta }^{\mathcal {U}})^{+\mathcal {M}_{\eta }^{\mathcal {U}}},\nu (E_{\beta }^{\mathcal {U}}))$
, where
![]() ${\eta = \operatorname {\mathrm {pred}}^{\mathcal {U}}(\beta +1)}$
. Thus, the set
${\eta = \operatorname {\mathrm {pred}}^{\mathcal {U}}(\beta +1)}$
. Thus, the set
![]() $\operatorname {\mathrm {HP}}_S^{M_{\infty }}$
is almost closed. Moreover, by arguments from the proof of Lemma 4.6 in [Reference Steel10] (using that the set of fixed points of
$\operatorname {\mathrm {HP}}_S^{M_{\infty }}$
is almost closed. Moreover, by arguments from the proof of Lemma 4.6 in [Reference Steel10] (using that the set of fixed points of
![]() $i^{\mathcal {T}}$
is S-thick) we have that for all
$i^{\mathcal {T}}$
is S-thick) we have that for all
![]() $\alpha <\Omega $
,
$\alpha <\Omega $
,
![]() $\mathcal {W}$
has the S-hull property at
$\mathcal {W}$
has the S-hull property at
![]() $\alpha $
iff
$\alpha $
iff
![]() $M_{\infty }$
has the S-hull property at
$M_{\infty }$
has the S-hull property at
![]() $i^{\mathcal {T}}(\alpha )$
.
$i^{\mathcal {T}}(\alpha )$
.
Suppose for the sake of contradiction that
![]() $\operatorname {\mathrm {HP}}_S^{\mathcal {W}}$
is not almost closed. Let
$\operatorname {\mathrm {HP}}_S^{\mathcal {W}}$
is not almost closed. Let
![]() $\delta <\Omega $
be a witness for this. Since
$\delta <\Omega $
be a witness for this. Since
![]() $\operatorname {\mathrm {HP}}_S^{M_{\infty }}$
is almost closed this means that
$\operatorname {\mathrm {HP}}_S^{M_{\infty }}$
is almost closed this means that
![]() $i^{\mathcal {T}}(\delta )>\sup (i^{\mathcal {T}}[\delta ])$
. There are two ways this can happen.
$i^{\mathcal {T}}(\delta )>\sup (i^{\mathcal {T}}[\delta ])$
. There are two ways this can happen.
Case 1.
There is
 $\beta +1\in [0,\Omega ]^{\mathcal {T}}$
such that
$\beta +1\in [0,\Omega ]^{\mathcal {T}}$
such that
 $\operatorname {\mathrm {crit}}(E_{\beta }^{\mathcal {T}})=i_{0\gamma }^{\mathcal {T}}(\delta )$
, where
$\operatorname {\mathrm {crit}}(E_{\beta }^{\mathcal {T}})=i_{0\gamma }^{\mathcal {T}}(\delta )$
, where
 $\gamma = \operatorname {\mathrm {pred}}_{\mathcal {T}}(\beta +1)$
.
$\gamma = \operatorname {\mathrm {pred}}_{\mathcal {T}}(\beta +1)$
.
Let us assume that
![]() $\beta $
is least such. Note that in this case we must have that
$\beta $
is least such. Note that in this case we must have that
![]() $\sup (i_{0\gamma }^{\mathcal {T}}[\delta ])=i_{0\gamma }^{\mathcal {T}}(\delta )$
and
$\sup (i_{0\gamma }^{\mathcal {T}}[\delta ])=i_{0\gamma }^{\mathcal {T}}(\delta )$
and
![]() $\delta ^{\prime }:=i_{0\gamma }^{\mathcal {T}}(\delta )\in \operatorname {\mathrm {HP}}_S^{M_{\infty }}.$
Since
$\delta ^{\prime }:=i_{0\gamma }^{\mathcal {T}}(\delta )\in \operatorname {\mathrm {HP}}_S^{M_{\infty }}.$
Since
![]() $\operatorname {\mathrm {crit}}(i_{\beta +1,\Omega }^{\mathcal {T}})>\delta ^{\prime }$
,
$\operatorname {\mathrm {crit}}(i_{\beta +1,\Omega }^{\mathcal {T}})>\delta ^{\prime }$
,
![]() $\mathcal {M}_{\beta +1}^{\mathcal {T}}$
has the S-hull property at
$\mathcal {M}_{\beta +1}^{\mathcal {T}}$
has the S-hull property at
![]() $\delta ^{\prime }$
. But then, since
$\delta ^{\prime }$
. But then, since
![]() $\mathcal {M}_{\beta +1}^{\mathcal {T}}$
has the S-hull property at
$\mathcal {M}_{\beta +1}^{\mathcal {T}}$
has the S-hull property at
![]() $\delta ^{\prime }$
and
$\delta ^{\prime }$
and
![]() $\mathcal {P}(\delta ^{\prime })\cap \mathcal {M}_{\gamma }^{\mathcal {T}}=\mathcal {P}(\delta ^{\prime })\cap \mathcal {M}_{\beta +1}^{\mathcal {T}}$
,
$\mathcal {P}(\delta ^{\prime })\cap \mathcal {M}_{\gamma }^{\mathcal {T}}=\mathcal {P}(\delta ^{\prime })\cap \mathcal {M}_{\beta +1}^{\mathcal {T}}$
,
![]() $\mathcal {M}_{\gamma }^{\mathcal {T}}$
has the S-hull property at
$\mathcal {M}_{\gamma }^{\mathcal {T}}$
has the S-hull property at
![]() $\delta ^{\prime }$
. Contradiction!
$\delta ^{\prime }$
. Contradiction!
Case 2.
 $ W \models "\delta \text { is singular with cofinality } \mu "$
and there is a minimal
$ W \models "\delta \text { is singular with cofinality } \mu "$
and there is a minimal
 $\alpha \in [0,\Omega ]^{\mathcal {T}}$
such that
$\alpha \in [0,\Omega ]^{\mathcal {T}}$
such that
 $i^{\mathcal {T}}_{0\alpha } (\mu ) = \operatorname {\mathrm {crit}}(i^{\mathcal {T}}_{\alpha \Omega })$
.
$i^{\mathcal {T}}_{0\alpha } (\mu ) = \operatorname {\mathrm {crit}}(i^{\mathcal {T}}_{\alpha \Omega })$
.
Let
![]() $\gamma + 1 \in [0,\Omega ]^{\mathcal {T}}$
such that
$\gamma + 1 \in [0,\Omega ]^{\mathcal {T}}$
such that
![]() $\operatorname {\mathrm {pred}}_{\mathcal {T}} (\gamma + 1) = \alpha $
and set
$\operatorname {\mathrm {pred}}_{\mathcal {T}} (\gamma + 1) = \alpha $
and set
![]() $W^{\prime }:=\mathcal {M}_{\alpha }^{\mathcal {T}}$
,
$W^{\prime }:=\mathcal {M}_{\alpha }^{\mathcal {T}}$
,
![]() $W^{\prime \prime }:=\mathcal {M}_{\gamma +1}^{\mathcal {T}}$
,
$W^{\prime \prime }:=\mathcal {M}_{\gamma +1}^{\mathcal {T}}$
,
![]() $\delta ^{\prime }:=i_{0\alpha }^{\mathcal {T}}(\delta )$
,
$\delta ^{\prime }:=i_{0\alpha }^{\mathcal {T}}(\delta )$
,
![]() $j:=i_{\alpha ,\gamma +1}^{\mathcal {T}}$
, and
$j:=i_{\alpha ,\gamma +1}^{\mathcal {T}}$
, and
![]() $\delta ^{\prime \prime }:=\sup (j[\delta ^{\prime }])$
. Note that
$\delta ^{\prime \prime }:=\sup (j[\delta ^{\prime }])$
. Note that
![]() $\delta ^{\prime \prime }<j(\delta ^{\prime })$
. Moreover, letting
$\delta ^{\prime \prime }<j(\delta ^{\prime })$
. Moreover, letting
![]() $i:=i_{0\alpha }^{\mathcal {T}}$
, we have that
$i:=i_{0\alpha }^{\mathcal {T}}$
, we have that
![]() $\delta ^{\prime }=i(\delta )=\sup (i[\delta ])$
.
$\delta ^{\prime }=i(\delta )=\sup (i[\delta ])$
.
Claim 1. The S-hull property holds at
![]() $\delta ^{\prime \prime }$
in
$\delta ^{\prime \prime }$
in
![]() $W^{\prime \prime }$
.
$W^{\prime \prime }$
.
Proof. Note that
![]() $\delta ^{\prime \prime }$
is a limit of
$\delta ^{\prime \prime }$
is a limit of
![]() $\operatorname {\mathrm {HP}}_S^{W^{\prime \prime }}$
and
$\operatorname {\mathrm {HP}}_S^{W^{\prime \prime }}$
and
![]() $\Omega \setminus \operatorname {\mathrm {HP}}_S^{W^{\prime \prime }}$
. So in order to see that the S-hull property holds at
$\Omega \setminus \operatorname {\mathrm {HP}}_S^{W^{\prime \prime }}$
. So in order to see that the S-hull property holds at
![]() $\delta ^{\prime \prime }$
in
$\delta ^{\prime \prime }$
in
![]() $W^{\prime \prime }$
it suffices to see that
$W^{\prime \prime }$
it suffices to see that
![]() $i_{\gamma +1,\Omega }^{\mathcal {T}}$
is continuous at
$i_{\gamma +1,\Omega }^{\mathcal {T}}$
is continuous at
![]() $\delta ^{\prime \prime }$
. To this end note that
$\delta ^{\prime \prime }$
. To this end note that
![]() $\operatorname {\mathrm {cof}}(\delta ^{\prime \prime })^{W^{\prime \prime }}=\kappa $
and that all extenders used along
$\operatorname {\mathrm {cof}}(\delta ^{\prime \prime })^{W^{\prime \prime }}=\kappa $
and that all extenders used along
![]() $[0,\Omega ]^{\mathcal {T}}$
after
$[0,\Omega ]^{\mathcal {T}}$
after
![]() $E_{\gamma }^{\mathcal {T}}$
have critical points greater than
$E_{\gamma }^{\mathcal {T}}$
have critical points greater than
![]() $\kappa $
. Thus,
$\kappa $
. Thus,
![]() $i_{\gamma +1,\Omega }^{\mathcal {T}}$
is continuous at
$i_{\gamma +1,\Omega }^{\mathcal {T}}$
is continuous at
![]() $\delta ^{\prime \prime }$
from which the claim follows.
$\delta ^{\prime \prime }$
from which the claim follows.
We claim that this implies that the S-hull property holds at
![]() $\delta ^{\prime }$
in
$\delta ^{\prime }$
in
![]() $W^{\prime }$
, which would be a contradiction. Let
$W^{\prime }$
, which would be a contradiction. Let
![]() $A\subset \delta ^{\prime }$
such that
$A\subset \delta ^{\prime }$
such that
![]() $A\in W^{\prime }$
and
$A\in W^{\prime }$
and
![]() $\Gamma $
be an S-thick set. We need to show that there is a term
$\Gamma $
be an S-thick set. We need to show that there is a term
![]() $\tau $
,
$\tau $
,
![]() $\vec {\xi }\in [\Gamma ]^{<\omega }$
, and
$\vec {\xi }\in [\Gamma ]^{<\omega }$
, and
![]() $\vec {\beta }\in [\delta ^{\prime }]^{<\omega }$
such that
$\vec {\beta }\in [\delta ^{\prime }]^{<\omega }$
such that
Note that
![]() $j(A)\cap \delta ^{\prime \prime }\in W^{\prime \prime }$
. Thus, there is a term
$j(A)\cap \delta ^{\prime \prime }\in W^{\prime \prime }$
. Thus, there is a term
![]() $\sigma $
,
$\sigma $
,
![]() $\vec {\zeta }\in [\Gamma ]^{<\omega }$
, and
$\vec {\zeta }\in [\Gamma ]^{<\omega }$
, and
![]() $\vec {\gamma }\in \delta ^{\prime \prime }$
such that
$\vec {\gamma }\in \delta ^{\prime \prime }$
such that
We may assume that j fixes
![]() $\vec {\zeta }$
. Let
$\vec {\zeta }$
. Let
![]() $\vec {\gamma }=([a_{0},f_{\!0}]_{E}^{W^{\prime }},...,[a_{n},f_{\!n}]_{E}^{W^{\prime }})$
, where for
$\vec {\gamma }=([a_{0},f_{\!0}]_{E}^{W^{\prime }},...,[a_{n},f_{\!n}]_{E}^{W^{\prime }})$
, where for
![]() $k\leq n$
,
$k\leq n$
,
![]() $a_{k}\in [\nu (E)]^{<\omega }$
and
$a_{k}\in [\nu (E)]^{<\omega }$
and
![]() $f_{\!k}\in {^{[\kappa ]^{<\omega }}W^{\prime }}\cap W^{\prime }$
. Note that by Łoś’s Theorem,
$f_{\!k}\in {^{[\kappa ]^{<\omega }}W^{\prime }}\cap W^{\prime }$
. Note that by Łoś’s Theorem,
 $$ \begin{align} j(\xi) & \in \sigma^{W^{\prime\prime}}[\vec{\zeta},\vec{\gamma}]\iff \nonumber\\ \{b\in[\kappa]^{<\omega}:W^{\prime} \models \xi & \in \sigma [\vec{\zeta},f_{0}^{a_{0},a}(b),...,f_{n}^{a_{n},a}(b)]\}\in E_{a}, \end{align} $$
$$ \begin{align} j(\xi) & \in \sigma^{W^{\prime\prime}}[\vec{\zeta},\vec{\gamma}]\iff \nonumber\\ \{b\in[\kappa]^{<\omega}:W^{\prime} \models \xi & \in \sigma [\vec{\zeta},f_{0}^{a_{0},a}(b),...,f_{n}^{a_{n},a}(b)]\}\in E_{a}, \end{align} $$
where
![]() $a=\bigcup _{i\leq n}a_{n}$
. Furthermore, for
$a=\bigcup _{i\leq n}a_{n}$
. Furthermore, for
![]() $\xi <\delta ^{\prime }$
,
$\xi <\delta ^{\prime }$
,
Note that for every
![]() $c\in [\nu (E)]^{<\omega }$
,
$c\in [\nu (E)]^{<\omega }$
,
![]() $E_{c}$
is close to
$E_{c}$
is close to
![]() $W^{\prime }$
. In particular, since
$W^{\prime }$
. In particular, since
![]() $W^{\prime }\models \text {ZFC}$
,
$W^{\prime }\models \text {ZFC}$
,
![]() $E_{c}\in W^{\prime }$
for every
$E_{c}\in W^{\prime }$
for every
![]() $c\in [\nu (E)]^{<\omega }$
. Moreover,
$c\in [\nu (E)]^{<\omega }$
. Moreover,
![]() $\delta ^{\prime }$
is a limit cardinal in
$\delta ^{\prime }$
is a limit cardinal in
![]() $W^{\prime }$
and
$W^{\prime }$
and
![]() $\text {GCH}$
holds in
$\text {GCH}$
holds in
![]() $W^{\prime }$
. Thus, for every
$W^{\prime }$
. Thus, for every
![]() $c\in [\nu (E)]^{<\omega }$
the ordinal of the measure
$c\in [\nu (E)]^{<\omega }$
the ordinal of the measure
![]() $E_{c}$
in the
$E_{c}$
in the
![]() $W^{\prime }$
-order
$W^{\prime }$
-order
![]() $<_{W^{\prime }}$
is an ordinal less than
$<_{W^{\prime }}$
is an ordinal less than
![]() $\delta ^{\prime }$
. Furthermore, as the ordinals below
$\delta ^{\prime }$
. Furthermore, as the ordinals below
![]() $\delta ^{\prime \prime }$
might be represented via functions bounded in
$\delta ^{\prime \prime }$
might be represented via functions bounded in
![]() $\delta ^{\prime }$
, we may assume that for
$\delta ^{\prime }$
, we may assume that for
![]() $k\leq n$
,
$k\leq n$
,
![]() $f_{\!k}$
is bounded in
$f_{\!k}$
is bounded in
![]() $\delta ^{\prime }$
and thus also their ordinals in the
$\delta ^{\prime }$
and thus also their ordinals in the
![]() $W^{\prime }$
-order are less than
$W^{\prime }$
-order are less than
![]() $\delta ^{\prime }$
. But this means that 5.1 and 5.2 give us a term
$\delta ^{\prime }$
. But this means that 5.1 and 5.2 give us a term
![]() $\tau $
and
$\tau $
and
![]() $\vec {\beta }\in [\delta ^{\prime }]^{<\omega }$
such that
$\vec {\beta }\in [\delta ^{\prime }]^{<\omega }$
such that
This finishes the proof of the theorem.
Acknowledgments
The first author would like to thank the organizers of the “5th Münster Conference on Inner Model Theory”, “Advances in Set Theory”, and the “Arctic Set Theory Workshop 6” for giving him the opportunity to present parts of this paper. Moreover, the authors would like to thank Tapio Saarinen, Philipp Schlicht, Shervin Sorouri, and the anonymous referee for their helpful feedback.
Funding
The first author was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – project number 445387776.
The second author was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics-Geometry-Structure.
The first author would like to thank the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics-Geometry-Structure for financial support in order to attend conferences and present material from this work.



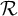
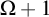



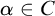
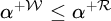
 -Woodin cardinal. On the other hand, we show that assuming there is no transitive model of KP with a Woodin cardinal the conjecture holds. In the course of this we will also show that if
-Woodin cardinal. On the other hand, we show that assuming there is no transitive model of KP with a Woodin cardinal the conjecture holds. In the course of this we will also show that if 





