Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T23:14:13.699Z Has data issue: false hasContentIssue false
  • English
  • Français

The M-valued calculus of non-contradiction

Published online by Cambridge University Press:  12 March 2014

Alan Rose
Alan Rose*
Affiliation:
The University, Nottingham, England
Get access Rights & Permissions [Opens in a new window]

Extract

The 2-valued calculus of non-contradiction of Dexter has been extended to 3-valued logic. The methods used were, however, too complicated to be capable of generalisation to m-valued logics. The object of the present paper is to give an alternative method of generalising Dexter's work to m-valued logics with one designated truth-value. The rule of procedure is generalised in the same way as before, but the deductive completeness of the system is proved by applying results of Rosser and Turquette. The system has an infinite set of primitive functions, written n(P1, P2, …, Pr) (r = 1,2, …). With the notation of Post, n(P1, P2, …, Pr) has the same truth-value as ~(P1 & P2 & … & Pr). Thus n(P) is Post's primitive ~P, and we can define & by

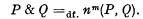
We use n2(P1, P2, …, Pr) as an abbreviation for n(n(P1, P2, …, Pr)); similarly for higher powers of n. But if we set up the 1-1 correspondence of truth-values i ↔ m−i+1, then & corresponds to ∨ and ~m−1 corresponds to ~. Hence the functional completeness of our system follows from a theorem of Post.

We define the functions N(P), N(P, Q) by

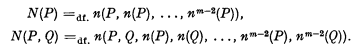
Thus the truth-value of N(P) is undesignated if and only if the truth-value of P is designated, and the truth-value of N(P, Q) is undesignated if and only if the truth-values of P and Q are both designated.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 18 , Issue 3 , September 1953 , pp. 237 - 241
Copyright
Copyright © Association for Symbolic Logic 1953

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Dexter, Glenn Edward, The calculus of non-contradiction, American journal of mathematics, vol. 65 (1943), pp. 171–178CrossRefGoogle Scholar.

2 Rose, Alan, An extension of the calculus of non-contradiction, Proceedings of the London Mathematical Society, second series vol. 54 (1952), pp. 184–200CrossRefGoogle Scholar.

3 See Post, Emil L., Introduction to a general theory of elementary propositions, American journal of mathematics, vol. 43 (1921), pp. 163–185CrossRefGoogle Scholar; also Łukasiewicz, Jan and Tarski, Alfred, Untersuchungen über den Aussagenkalkül, Comptes rendus des séances de la Société des Sciences et des Lettres de Varsovie, Classe III, vol. 23 (1930), pp. 30–50Google Scholar.

4 Rosser, J. B. and Turquette, A. R., Axiom schemes for m-valued propositional calculi, this Journal, vol. 10 (1945), pp. 61–82Google Scholar; A note on the deductive completeness of m-valued propositional calculi, this Journal, vol. 14 (1949), pp. 219–225Google Scholar.

5 Op. cit.

6 Op. cit.

7 Op. cit.

8 Op. cit.

9 Op. cit.

10 Op. cit.

11 Op. cit.