Published online by Cambridge University Press: 12 March 2014
If two nonstandard models of complete arithmetic are elementarily embedded in a third, then their intersection may be considerably smaller than either of them; indeed, the intersection may be only the standard model. For example, if D and E are nonprincipal ultrafilters on ω, then the nonstandard models D-prod 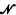 and E-prod
and E-prod 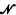 (where
(where 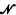 is the standard model) have canonical elementary embeddings into D-prod (E-prod
is the standard model) have canonical elementary embeddings into D-prod (E-prod 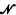 , and the intersection of their images is easily seen to be the (canonical image of the) standard model. In this paper, we shall prove that, under certain conditions, this phenomenon will not occur. Our main result (Theorem 3) is that the intersection of countably many pairwise cofinal models is itself cofinal with these models, provided that at least one of them is generated by a single element. (Precise definitions will be given below.)
, and the intersection of their images is easily seen to be the (canonical image of the) standard model. In this paper, we shall prove that, under certain conditions, this phenomenon will not occur. Our main result (Theorem 3) is that the intersection of countably many pairwise cofinal models is itself cofinal with these models, provided that at least one of them is generated by a single element. (Precise definitions will be given below.)
The theorems in this paper were first formulated in terms of ultrafilters, then rephrased (using the methods of Chapter III of [1]) as statements about ultra-powers of 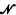 , and finally generalized to their present form. Since the theorems and their proofs are now entirely model-theoretic, they are presented here separately from the study of ultrafilters in which they originated. That study, including applications of the present results, will appear in [2].
, and finally generalized to their present form. Since the theorems and their proofs are now entirely model-theoretic, they are presented here separately from the study of ultrafilters in which they originated. That study, including applications of the present results, will appear in [2].
Let L be the first-order language whose n-place relation symbols are all the relations R ⊆; ωn and whose n-place function symbols are all the functions f: ωn → ω. Let 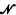 be the standard model for L; its universe is ω and every nonlogical symbol of L denotes itself. Let
be the standard model for L; its universe is ω and every nonlogical symbol of L denotes itself. Let 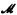 be an elementary extension of
be an elementary extension of 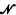 . The relation (or function) denoted by R (or f) in
. The relation (or function) denoted by R (or f) in  will be called *R (or *f).
will be called *R (or *f).