Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T20:13:00.530Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinitary logics and very sparse random graphs

Published online by Cambridge University Press:  12 March 2014

James F. Lynch
James F. Lynch*
Affiliation:
Department of Mathematics and Computer Science, Clarkson University, Potsdam, NY 13699-5815, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 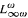be the infinitary language obtained from the first-order language of graphs by closure under conjunctions and disjunctions of arbitrary sets of formulas, provided only finitely many distinct variables occur among the formulas. Let p(n) be the edge probability of the random graph on n vertices. It is shown that if p(n) ≪ n−1 satisfies certain simple conditions on its growth rate, then for every 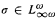, the probability that σ holds for the random graph on n vertices converges. In fact, if p(n) = n−α, α > 1, then the probability is either smaller than 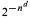for some d > 0, or it is asymptotic to cn−d for some c > 0, d ≥ 0. Results on the difficulty of computing the asymptotic probability are given.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 2 , June 1997 , pp. 609 - 623
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Behrendt, T., Compton, K., and Grädel, E., Optimization problems: expressibility, approximation properties and expected asymptotic growth of optimal solutions, Proc. conf. on computer science logic, Springer-Verlag, New York, 1993.Google Scholar
[2] Butler, R. W. and Finelli, G. B., The infeasability of experimental quantification of life-critical software reliability, Software Engineering Notes, vol. 16 (1991), pp. 66–76.CrossRefGoogle Scholar
[3] Chandra, A. and Harel, D., Structure and complexity of relational queries, Journal of Computer and System Sciences, vol. 25 (1982), pp. 99–128.CrossRefGoogle Scholar
[4] Chernoff, H., A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations, Ann. Math. Stat., vol. 23 (1952), pp. 493–507.CrossRefGoogle Scholar
[5] Compton, K. J. and Ravishankar, C., Expected deadlock time in a multiprocessing system, Journal of the ACM, vol. 42 (1995), pp. 562–583.CrossRefGoogle Scholar
[6] Erdős, P. and Rényi, A., On the evolution of random graphs, Magyar Tud. Akad. Mat. Kutató Int. Kőzl., vol. 5 (1960), pp. 17–61.Google Scholar
[7] Fagin, R., Probabilities on finite models, this Journal, vol. 41 (1976), pp. 50–58.Google Scholar
[8] Flajolet, P., Knuth, D. E., and Pittel, B., The first cycles in an evolving graph, Discrete Mathematics, vol. 75 (1989), pp. 167–215.CrossRefGoogle Scholar
[9] Glebskiĭ, Y. V., Kogan, D. I., Liogon'kiĭ, M.I., and Talanov, V. A., Range and degree of readability of formulas in the restricted predicate calculus, Kibernetika (Kiev), vol. 2 (1969), pp. 17–28, English translation, Cybernetics, vol. 5 (1972), pp. 142–154.Google Scholar
[10] Gurevich, Y., Zero-one laws, Bulletin of the EATCS, vol. 46 (1992), pp. 90–106.Google Scholar
[11] Kolaitis, Ph. G., On asymptotic probabilities of inductive queries and their decision problem, Logics of programs '85 (Parikh, R., editor), Lecture Notes in Computer Science, vol. 193, Springer-Verlag, 1985, pp. 153–166.CrossRefGoogle Scholar
[12] Kolaitis, Ph. G. and Vardi, M. Y., Infinitary logics and 0-1 laws, Information and Computation, vol. 98 (1992), pp. 258–294.CrossRefGoogle Scholar
[13] Lynch, J. F., Probabilities of first-order sentences about unary functions, Transactions of the American Mathematical Society, vol. 287 (1985), pp. 543–568.CrossRefGoogle Scholar
[14] Lynch, J. F., Probabilities of sentences about very sparse random graphs, Random Structures and Algorithms, vol. 3 (1992), pp. 33–53.CrossRefGoogle Scholar
[15] Lynch, J. F., An extension of 0-1 laws, Random Structures and Algorithms, vol. 5 (1994),pp. 155–172.CrossRefGoogle Scholar
[16] Lynch, J. F., Random resource allocation graphs and the probability of deadlock, SIAM Journal on Discrete Mathematics, vol. 7 (1994), pp. 458–473.CrossRefGoogle Scholar
[17] Ruciński, A. and Vince, A., Strongly balanced graphs and random graphs, Journal of Graph Theory, vol. 10 (1986), pp. 251–264.CrossRefGoogle Scholar
[18] Shelah, S. and Spencer, J., Zero-one laws for sparse random graphs, Journal of the American Mathematical Society, vol. 1 (1988), pp. 97–115.CrossRefGoogle Scholar
[19] Tyszkiewicz, J., Infinitary queries and their asymptotic probabilities. I. Properties definable in transitive closure logic, Proceedings of Computer Science Logic '91 (Börger, E.et al., editors), Lecture Notes in Computer Science, vol. 626, Springer-Verlag, 1991, pp. 396–410.CrossRefGoogle Scholar