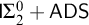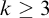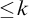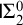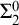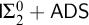1 Introduction
One of the major initiatives in reverse mathematics is the logical analysis of theorems of countable combinatorics, with special attention to Ramsey’s theorem for pairs and its consequences [Reference Cholak, Jockusch and Slaman5, Reference Chong, Slaman and Yang7–Reference Chong, Slaman and Yang9, Reference Hirschfeldt and Shore16, Reference Lerman, Solomon and Towsner21–Reference Liu23, Reference Patey and Yokoyama27, Reference Seetapun and Slaman29, Reference Slaman and Yokoyama31]. We continue this tradition by analyzing the second of two theorems from On the adjacency of vertices to the vertices of an infinite subgraph by Rival and Sands [Reference Rival and Sands28]. To the best of our knowledge, this analysis yields the first examples of theorems from the general mathematics literature whose strength is exactly characterized by the ascending/descending sequence principle.
Both of the Rival–Sands theorems are inspired by Ramsey’s theorem for pairs and two colors. The first theorem is a hybrid inside/outside version of Ramsey’s theorem for pairs. Thinking in terms of graphs, Ramsey’s theorem for pairs produces an infinite set of vertices H that is either a clique or an independent set in a given countable graph. However, Ramsey’s theorem provides no information concerning the relationship between the vertices inside H and the vertices outside H. The Rival–Sands theorem for graphs balances this situation by producing an infinite set of vertices H that is not necessarily a clique or an independent set, but for which there is information concerning the relationship between the vertices inside H and the vertices outside H.
Rival–Sands theorem for graphs [Reference Rival and Sands28].
Every infinite graph G contains an infinite subset H such that every vertex of G is adjacent to precisely none, one, or infinitely many vertices of H.
Rival and Sands note that the three options “none,” “one,” and “infinitely many” in their theorem are all necessary. They ask for a class of graphs for which the “one” option may be removed, and they show that this is possible for the class of comparability graphs of infinite partial orders of finite width (i.e., infinite partial orders for which there is a fixed finite upper bound on the size of the antichains). We call the resulting theorem the Rival–Sands theorem for partial orders.
Rival–Sands theorem for partial orders [Reference Rival and Sands28].
Every infinite partial order P of finite width contains an infinite chain C such that every element of P is either comparable with no element of C or with infinitely many elements of C.
Furthermore, Rival and Sands show that in the case of countable partial orders, the “infinitely many” option may be strengthened to “cofinitely many.”
The Rival–Sands theorems do not appear to be immediate consequences of any version of Ramsey’s theorem, and neither Rival–Sands theorem appears to be an immediate consequence of the other. Rival and Sands give direct proofs of both theorems that do not invoke any other Ramsey-theoretic statement. Interestingly, their proof of the Rival–Sands theorem for partial orders makes essential use of
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
by iterating a maximal chain principle that is equivalent to
$\Pi ^1_1\text {-}\mathsf {CA}_0$
by iterating a maximal chain principle that is equivalent to
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
over
$\Pi ^1_1\text {-}\mathsf {CA}_0$
over
![]() $\mathsf {RCA}_0$
. We discuss this in detail in Section 8.
$\mathsf {RCA}_0$
. We discuss this in detail in Section 8.
In [Reference Fiori-Carones, Shafer and Soldà11], Fiori-Carones, Shafer, and Soldà analyze the axiomatic and computational strength of the Rival–Sands theorem for graphs in the style of reverse mathematics and Weihrauch analysis. In reverse mathematics, the Rival–Sands theorem for graphs is equivalent to
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
. Thus the Rival–Sands theorem for graphs is indirectly equivalent to Ramsey’s theorem for triples (which is also equivalent to
$\mathsf {RCA}_0$
. Thus the Rival–Sands theorem for graphs is indirectly equivalent to Ramsey’s theorem for triples (which is also equivalent to
![]() $\mathsf {ACA}_0$
; see [Reference Simpson30]), but it does not follow from Ramsey’s theorem for pairs (which is strictly weaker than
$\mathsf {ACA}_0$
; see [Reference Simpson30]), but it does not follow from Ramsey’s theorem for pairs (which is strictly weaker than
![]() $\mathsf {ACA}_0$
[Reference Seetapun and Slaman29]). However, the authors of [Reference Fiori-Carones, Shafer and Soldà11] together with Hirst and Lempp show that a weakened inside-only version of the Rival–Sands theorem for graphs is indeed equivalent to Ramsey’s theorem for pairs and two colors. In terms of the Weihrauch degrees, the main result of [Reference Fiori-Carones, Shafer and Soldà11] is that the Rival–Sands theorem for graphs is strongly Weihrauch-equivalent to the double-jump of weak König’s lemma. To the best of the authors’ knowledge, the Rival–Sands theorem for graphs is the first theorem from the general mathematics literature exhibiting exactly this strength. Furthermore, combining the aforementioned equivalence with a result of Brattka and Rakotoniaina [Reference Brattka and Rakotoniaina4] yields that the Rival–Sands theorem for graphs is Weihrauch-equivalent to the parallelization of Ramsey’s theorem for pairs and two colors. Thus the uniform computational strength of the Rival–Sands theorem for graphs is exactly characterized by the ability to simultaneously solve countably many instances of Ramsey’s theorem for pairs in parallel.
$\mathsf {ACA}_0$
[Reference Seetapun and Slaman29]). However, the authors of [Reference Fiori-Carones, Shafer and Soldà11] together with Hirst and Lempp show that a weakened inside-only version of the Rival–Sands theorem for graphs is indeed equivalent to Ramsey’s theorem for pairs and two colors. In terms of the Weihrauch degrees, the main result of [Reference Fiori-Carones, Shafer and Soldà11] is that the Rival–Sands theorem for graphs is strongly Weihrauch-equivalent to the double-jump of weak König’s lemma. To the best of the authors’ knowledge, the Rival–Sands theorem for graphs is the first theorem from the general mathematics literature exhibiting exactly this strength. Furthermore, combining the aforementioned equivalence with a result of Brattka and Rakotoniaina [Reference Brattka and Rakotoniaina4] yields that the Rival–Sands theorem for graphs is Weihrauch-equivalent to the parallelization of Ramsey’s theorem for pairs and two colors. Thus the uniform computational strength of the Rival–Sands theorem for graphs is exactly characterized by the ability to simultaneously solve countably many instances of Ramsey’s theorem for pairs in parallel.
In this work, we characterize the axiomatic strength of the Rival–Sands theorem for partial orders in terms of the ascending/descending sequence principle, which states that an infinite linear order contains either an infinite ascending sequence or an infinite descending sequence. Our primary focus is the Rival–Sands theorem for partial orders as stated above, but we also consider the version with “cofinitely many” in place of “infinitely many.” The main results are the following, which are summarized in Theorem 6.6.
-
• The Rival–Sands theorem for infinite partial orders of arbitrary finite width is equivalent to the ascending/descending sequence principle plus the
 $\Sigma ^0_2$
induction scheme over
$\Sigma ^0_2$
induction scheme over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
. -
• For each fixed standard
 $k \geq 3$
, the Rival–Sands theorem for infinite partial orders of width
$k \geq 3$
, the Rival–Sands theorem for infinite partial orders of width
 $\leq \! k$
is equivalent to the ascending/descending sequence principle over
$\leq \! k$
is equivalent to the ascending/descending sequence principle over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
. -
• The Rival–Sands theorem for infinite partial orders that are decomposable into the union of two chains is equivalent to the stable ascending/descending sequence principle over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
. -
• The Rival–Sands theorem with “cofinitely many” in place of “infinitely many” for infinite partial orders of width
 $\leq \! 2$
is equivalent to the ascending/descending sequence principle over
$\leq \! 2$
is equivalent to the ascending/descending sequence principle over
 $\mathsf {RCA}_0$
plus the
$\mathsf {RCA}_0$
plus the
 $\Sigma ^0_2$
induction scheme.
$\Sigma ^0_2$
induction scheme.
Furthermore, in Theorems 7.2 and 7.3, we give a new purely combinatorial result by extending the Rival–Sands theorem to all countably infinite partial orders that do not have infinite antichains. This is non-trivial, as a partial order may have arbitrarily large finite antichains, and therefore not have finite width, yet still have no infinite antichain. In Theorem 7.8, we also show that the extension of the Rival–Sands theorem to countably infinite partial orders without infinite antichains is equivalent to
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Computational aspects of linear and partial orders have long been studied. In reverse mathematics, the ascending/descending sequence principle is a weak consequence of Ramsey’s theorem for pairs that was first isolated and studied by Hirschfeldt and Shore [Reference Hirschfeldt and Shore16]. There are a few classical statements that are readily equivalent to this principle over
![]() $\mathsf {RCA}_0$
, such as the statement “Every countable sequence of real numbers contains a monotone subsequence” (see [Reference Kreuzer20, Remark 6.8]), but thus far the principle’s primary use has been as an important technical benchmark. To the best of our knowledge, Theorem 6.6 provides the first examples from the modern mathematical literature of theorems that are equivalent to the ascending/descending sequence principle, the ascending/descending sequence principle plus
$\mathsf {RCA}_0$
, such as the statement “Every countable sequence of real numbers contains a monotone subsequence” (see [Reference Kreuzer20, Remark 6.8]), but thus far the principle’s primary use has been as an important technical benchmark. To the best of our knowledge, Theorem 6.6 provides the first examples from the modern mathematical literature of theorems that are equivalent to the ascending/descending sequence principle, the ascending/descending sequence principle plus
![]() $\Sigma ^0_2$
induction, and to the stable ascending/descending sequence principle. This explains our title. It is extraordinary to find theorems from the ordinary literature that are equivalent to the ascending/descending sequence principle.
$\Sigma ^0_2$
induction, and to the stable ascending/descending sequence principle. This explains our title. It is extraordinary to find theorems from the ordinary literature that are equivalent to the ascending/descending sequence principle.
It follows from our analysis that the Rival–Sands theorem for partial orders without infinite antichains is equivalent to the Rival–Sands theorem for graphs, whereas the Rival–Sands theorem for partial orders of finite width is strictly weaker. The relationship between the Rival–Sands theorem for partial orders and Ramsey’s theorem for pairs is more curious. Ramsey’s theorem for pairs and two colors suffices to prove the Rival–Sands theorem for partial orders of width k for any fixed k, but not for partial orders of arbitrary finite width. However, Ramsey’s theorem for pairs and arbitrarily many colors does suffice to prove the Rival–Sands theorem for partial orders of arbitrary finite width. This is a matter of induction. Ramsey’s theorem for pairs and two colors does not prove the
![]() $\Sigma ^0_2$
induction scheme [Reference Chong, Slaman and Yang9], but Ramsey’s theorem for pairs and arbitrarily many colors does [Reference Hirst17]. All together, the Rival–Sands theorem for partial orders of arbitrary finite width is strictly weaker than Ramsey’s theorem for pairs and arbitrarily many colors; the Rival–Sands theorem for partial orders of arbitrary finite width is not provable from Ramsey’s theorem for pairs and two colors; and the Rival–Sands theorem for partial orders of a fixed finite width k is strictly weaker than Ramsey’s theorem for pairs and two colors.
$\Sigma ^0_2$
induction scheme [Reference Chong, Slaman and Yang9], but Ramsey’s theorem for pairs and arbitrarily many colors does [Reference Hirst17]. All together, the Rival–Sands theorem for partial orders of arbitrary finite width is strictly weaker than Ramsey’s theorem for pairs and arbitrarily many colors; the Rival–Sands theorem for partial orders of arbitrary finite width is not provable from Ramsey’s theorem for pairs and two colors; and the Rival–Sands theorem for partial orders of a fixed finite width k is strictly weaker than Ramsey’s theorem for pairs and two colors.
This article is organized as follows. Section 2 gives an overview of the relevant reverse mathematics background. Section 3 formalizes several versions of the Rival–Sands theorem for partial orders and discusses principles concerning chains in partial orders, most notably Kierstead’s effective analog of Dilworth’s theorem [Reference Kierstead18]. Section 4 presents our first proofs of the Rival–Sands theorem for partial orders. These proofs are not axiomatically optimal, but they are easy to understand, and they introduce ideas that we later effectivize in order to give proofs in weaker systems. Section 5 provides the forward directions of the equivalences mentioned above. Section 6 provides the reversals. Section 7 provides our extension of the Rival–Sands theorem to infinite partial orders without infinite antichains as well as a proof that this extension is equivalent to
![]() $\mathsf {ACA}_0$
. All the proofs of the Rival–Sands theorem for partial orders and its variants given in Sections 4–7 are new. In Section 8, we discuss the original proof by Rival and Sands, and we analyze several principles asserting that partial orders contain various sorts of maximal chains.
$\mathsf {ACA}_0$
. All the proofs of the Rival–Sands theorem for partial orders and its variants given in Sections 4–7 are new. In Section 8, we discuss the original proof by Rival and Sands, and we analyze several principles asserting that partial orders contain various sorts of maximal chains.
2 Reverse mathematics background
We give a brief review of
![]() $\mathsf {RCA}_0$
,
$\mathsf {RCA}_0$
,
![]() $\mathsf {WKL}_0$
,
$\mathsf {WKL}_0$
,
![]() $\mathsf {ACA}_0$
,
$\mathsf {ACA}_0$
,
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
, Ramsey’s theorem for pairs, its combinatorial consequences, and the first-order schemes. For further details, we refer the reader to Simpson’s standard reference [Reference Simpson30] and to Hirschfeldt’s monograph [Reference Hirschfeldt15].
$\Pi ^1_1\text {-}\mathsf {CA}_0$
, Ramsey’s theorem for pairs, its combinatorial consequences, and the first-order schemes. For further details, we refer the reader to Simpson’s standard reference [Reference Simpson30] and to Hirschfeldt’s monograph [Reference Hirschfeldt15].
We work in the two-sorted language of second-order arithmetic
![]() $0$
,
$0$
,
![]() $1$
,
$1$
,
![]() $<$
,
$<$
,
![]() $+$
,
$+$
,
![]() $\times $
,
$\times $
,
![]() $\in $
, where variables x, y, z, etc. typically range over the first sort, thought of as natural numbers, and variables X, Y, Z, etc. typically range over the second sort, thought of as sets of natural numbers. As usual, the symbol
$\in $
, where variables x, y, z, etc. typically range over the first sort, thought of as natural numbers, and variables X, Y, Z, etc. typically range over the second sort, thought of as sets of natural numbers. As usual, the symbol
![]() $\mathbb {N}$
denotes the first-order part of whatever structure is under consideration.
$\mathbb {N}$
denotes the first-order part of whatever structure is under consideration.
The axioms of the base system
![]() $\mathsf {RCA}_0$
(for recursive comprehension axiom) are as follows:
$\mathsf {RCA}_0$
(for recursive comprehension axiom) are as follows:
-
• A first-order sentence expressing that
 $(\mathbb {N}; 0, 1, <, +, \times )$
forms a discretely ordered commutative semi-ring with identity.
$(\mathbb {N}; 0, 1, <, +, \times )$
forms a discretely ordered commutative semi-ring with identity. -
• The
 $\Sigma ^0_1$
induction scheme (denoted
$\Sigma ^0_1$
induction scheme (denoted
 $\mathsf {I}\Sigma ^0_{1}$
), which consists of the universal closures (by both first- and second-order quantifiers) of all formulas of the form where
$\mathsf {I}\Sigma ^0_{1}$
), which consists of the universal closures (by both first- and second-order quantifiers) of all formulas of the form where $$ \begin{align*} \bigl(\varphi(0) \;\wedge\; \forall n \, (\varphi(n) \;\rightarrow\; \varphi(n+1))\bigr) \;\rightarrow\; \forall n \, \varphi(n), \end{align*} $$
$$ \begin{align*} \bigl(\varphi(0) \;\wedge\; \forall n \, (\varphi(n) \;\rightarrow\; \varphi(n+1))\bigr) \;\rightarrow\; \forall n \, \varphi(n), \end{align*} $$
 $\varphi $
is
$\varphi $
is
 $\Sigma ^0_1$
.
$\Sigma ^0_1$
.
-
• The
 $\Delta ^0_1$
comprehension scheme, which consists of the universal closures (by both first- and second-order quantifiers) of all formulas of the form where
$\Delta ^0_1$
comprehension scheme, which consists of the universal closures (by both first- and second-order quantifiers) of all formulas of the form where $$ \begin{align*} \forall n \, \bigl(\varphi(n) \;\leftrightarrow\; \psi(n)\bigr) \;\rightarrow\; \exists X \, \forall n \, \bigl(n \in X \;\leftrightarrow\; \varphi(n)\bigr), \end{align*} $$
$$ \begin{align*} \forall n \, \bigl(\varphi(n) \;\leftrightarrow\; \psi(n)\bigr) \;\rightarrow\; \exists X \, \forall n \, \bigl(n \in X \;\leftrightarrow\; \varphi(n)\bigr), \end{align*} $$
 $\varphi $
is
$\varphi $
is
 $\Sigma ^0_1$
,
$\Sigma ^0_1$
,
 $\psi $
is
$\psi $
is
 $\Pi ^0_1$
, and X is not free in
$\Pi ^0_1$
, and X is not free in
 $\varphi $
.
$\varphi $
.
The “
![]() $0$
” in “
$0$
” in “
![]() $\mathsf {RCA}_0$
” refers to the restriction of the induction scheme to
$\mathsf {RCA}_0$
” refers to the restriction of the induction scheme to
![]() $\Sigma ^0_1$
formulas.
$\Sigma ^0_1$
formulas.
![]() $\mathsf {RCA}_0$
suffices to implement the usual bijective encodings of pairs of numbers, finite sequences of numbers, finite sets of numbers, and so on. See [Reference Simpson30, Section II.2] for details on how this is done. For example, we may encode a function
$\mathsf {RCA}_0$
suffices to implement the usual bijective encodings of pairs of numbers, finite sequences of numbers, finite sets of numbers, and so on. See [Reference Simpson30, Section II.2] for details on how this is done. For example, we may encode a function
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
by its graph
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
by its graph
![]() $\{\langle m, n \rangle : f(m) = n\}$
. We may also encode the set
$\{\langle m, n \rangle : f(m) = n\}$
. We may also encode the set
![]() $\mathbb {N}^{<\mathbb {N}}$
of all finite sequences of natural numbers and the set
$\mathbb {N}^{<\mathbb {N}}$
of all finite sequences of natural numbers and the set
![]() $2^{<\mathbb {N}}$
of all finite binary sequences. For
$2^{<\mathbb {N}}$
of all finite binary sequences. For
![]() $\sigma , \tau \in \mathbb {N}^{<\mathbb {N}}$
and
$\sigma , \tau \in \mathbb {N}^{<\mathbb {N}}$
and
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
, let
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
, let
![]() $|\sigma |$
denote the length of
$|\sigma |$
denote the length of
![]() $\sigma $
; let
$\sigma $
; let
![]() $\tau \preceq \sigma $
denote that
$\tau \preceq \sigma $
denote that
![]() $\tau $
is an initial segment of
$\tau $
is an initial segment of
![]() $\sigma $
:
$\sigma $
:
![]() $|\tau | \leq |\sigma | \;\wedge \; \forall n < |\tau | \; (\tau (n) = \sigma (n))$
; and let
$|\tau | \leq |\sigma | \;\wedge \; \forall n < |\tau | \; (\tau (n) = \sigma (n))$
; and let
![]() $\tau \preceq f$
denote that
$\tau \preceq f$
denote that
![]() $\tau $
is an initial segment of f:
$\tau $
is an initial segment of f:
![]() $\forall n < |\tau | \; (\tau (n) = f(n))$
. For
$\forall n < |\tau | \; (\tau (n) = f(n))$
. For
![]() $\sigma , \tau \in \mathbb {N}^{<\mathbb {N}}$
, let
$\sigma , \tau \in \mathbb {N}^{<\mathbb {N}}$
, let
![]() $\sigma ^{\smallfrown } \tau $
denote the concatenation of
$\sigma ^{\smallfrown } \tau $
denote the concatenation of
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
. When
$\tau $
. When
![]() $\tau = \langle n \rangle $
is a sequence of length
$\tau = \langle n \rangle $
is a sequence of length
![]() $1$
, we usually write
$1$
, we usually write
![]() $\sigma ^{\smallfrown } n$
instead of
$\sigma ^{\smallfrown } n$
instead of
![]() $\sigma ^{\smallfrown } \langle n \rangle $
. For
$\sigma ^{\smallfrown } \langle n \rangle $
. For
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
,
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
,
![]() $\sigma \in \mathbb {N}^{<\mathbb {N}}$
, and
$\sigma \in \mathbb {N}^{<\mathbb {N}}$
, and
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $f {\restriction } n = \langle f(0), f(1), \dots , f(n-1) \rangle $
denote the initial segment of f of length n; and if
$f {\restriction } n = \langle f(0), f(1), \dots , f(n-1) \rangle $
denote the initial segment of f of length n; and if
![]() $n \leq |\sigma |$
, let
$n \leq |\sigma |$
, let
![]() $\sigma {\restriction } n = \langle \sigma (0), \dots , \sigma (n-1) \rangle $
denote the initial segment of
$\sigma {\restriction } n = \langle \sigma (0), \dots , \sigma (n-1) \rangle $
denote the initial segment of
![]() $\sigma $
of length n.
$\sigma $
of length n.
![]() $\mathsf {RCA}_0$
also suffices to develop the basic theory of oracle Turing machines (see, for example, [Reference Simpson30, Section VII.1]). We view such machines as defining Turing functionals, and we write
$\mathsf {RCA}_0$
also suffices to develop the basic theory of oracle Turing machines (see, for example, [Reference Simpson30, Section VII.1]). We view such machines as defining Turing functionals, and we write
![]() $\Phi (A)$
for the result of applying the functional
$\Phi (A)$
for the result of applying the functional
![]() $\Phi $
to the set A. We also write
$\Phi $
to the set A. We also write
![]() $\Phi (A)(n)$
for the value of
$\Phi (A)(n)$
for the value of
![]() $\Phi (A)$
on input n, if it is defined. We may relativize a Turing functional
$\Phi (A)$
on input n, if it is defined. We may relativize a Turing functional
![]() $\Phi $
to a set X, write
$\Phi $
to a set X, write
![]() $\Phi ^X$
to denote the relativized functional, and write
$\Phi ^X$
to denote the relativized functional, and write
![]() $\Phi ^X(A)$
for
$\Phi ^X(A)$
for
![]() $\Phi (X \oplus A)$
, where
$\Phi (X \oplus A)$
, where
![]() $X \oplus A = \{2n : n \in X\} \cup \{2n+1 : n \in A\}$
as usual. The
$X \oplus A = \{2n : n \in X\} \cup \{2n+1 : n \in A\}$
as usual. The
![]() $\Phi ^X(A)$
notation is intended to convey that X is fixed but A may vary. We may also iterate a sequence
$\Phi ^X(A)$
notation is intended to convey that X is fixed but A may vary. We may also iterate a sequence
![]() $\Phi _0, \dots , \Phi _{k-1}$
of Turing functionals. For a set A, we say that the iteration
$\Phi _0, \dots , \Phi _{k-1}$
of Turing functionals. For a set A, we say that the iteration
![]() $\Phi _{k-1}(\Phi _{k-2}(\cdots \Phi _0(A)\cdots ))$
is total if
$\Phi _{k-1}(\Phi _{k-2}(\cdots \Phi _0(A)\cdots ))$
is total if
![]() $\Phi _i(\Phi _{i-1}(\cdots \Phi _0(A)\cdots ))(n)$
is defined for every
$\Phi _i(\Phi _{i-1}(\cdots \Phi _0(A)\cdots ))(n)$
is defined for every
![]() $i < k$
and every n. This may be expressed by asserting that for every n, there is a sequence
$i < k$
and every n. This may be expressed by asserting that for every n, there is a sequence
![]() $\langle \sigma _0, \dots , \sigma _k \rangle $
of elements of
$\langle \sigma _0, \dots , \sigma _k \rangle $
of elements of
![]() $\mathbb {N}^{<\mathbb {N}}$
, each of length at least n, such that
$\mathbb {N}^{<\mathbb {N}}$
, each of length at least n, such that
![]() $\sigma _0 \preceq A$
and
$\sigma _0 \preceq A$
and
![]() $\forall i < k\; \forall m < |\sigma _{i+1}|\; \bigl (\Phi _i(\sigma _i)(m) \text { halts within } |\sigma _i| \text { steps and } \sigma _{i+1}(m) = \Phi _i(\sigma _i)(m)\bigr )$
.
$\forall i < k\; \forall m < |\sigma _{i+1}|\; \bigl (\Phi _i(\sigma _i)(m) \text { halts within } |\sigma _i| \text { steps and } \sigma _{i+1}(m) = \Phi _i(\sigma _i)(m)\bigr )$
.
Define a tree to be a set
![]() $T \subseteq \mathbb {N}^{<\mathbb {N}}$
that is closed under initial segments:
$T \subseteq \mathbb {N}^{<\mathbb {N}}$
that is closed under initial segments:
![]() $\forall \sigma \, \forall \tau \, ((\sigma \in T \;\wedge \; \tau \preceq \sigma ) \;\rightarrow \; \tau \in T)$
. Say that an
$\forall \sigma \, \forall \tau \, ((\sigma \in T \;\wedge \; \tau \preceq \sigma ) \;\rightarrow \; \tau \in T)$
. Say that an
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
is a infinite path through a tree T if every initial segment of f is in T:
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
is a infinite path through a tree T if every initial segment of f is in T:
![]() $\forall n \, (f {\restriction } n \in T)$
. A tree with no infinite path is called well-founded, and a tree with an infinite path is called ill-founded. Finally, a tree
$\forall n \, (f {\restriction } n \in T)$
. A tree with no infinite path is called well-founded, and a tree with an infinite path is called ill-founded. Finally, a tree
![]() $T \subseteq \mathbb {N}^{<\mathbb {N}}$
is called finitely branching if for every
$T \subseteq \mathbb {N}^{<\mathbb {N}}$
is called finitely branching if for every
![]() $\sigma \in T$
there are only finitely many n with
$\sigma \in T$
there are only finitely many n with
![]() $\sigma ^{\smallfrown } n \in T$
. A tree
$\sigma ^{\smallfrown } n \in T$
. A tree
![]() $T \subseteq 2^{<\mathbb {N}}$
is necessarily finitely branching. All of these definitions can be made in
$T \subseteq 2^{<\mathbb {N}}$
is necessarily finitely branching. All of these definitions can be made in
![]() $\mathsf {RCA}_0$
. The axioms of
$\mathsf {RCA}_0$
. The axioms of
![]() $\mathsf {WKL}_0$
(for weak König’s lemma) are those of
$\mathsf {WKL}_0$
(for weak König’s lemma) are those of
![]() $\mathsf {RCA}_0$
, plus the statement that every infinite tree
$\mathsf {RCA}_0$
, plus the statement that every infinite tree
![]() $T \subseteq 2^{<\mathbb {N}}$
has an infinite path.
$T \subseteq 2^{<\mathbb {N}}$
has an infinite path.
The axioms of
![]() $\mathsf {ACA}_0$
(for arithmetical comprehension axiom) are of those of
$\mathsf {ACA}_0$
(for arithmetical comprehension axiom) are of those of
![]() $\mathsf {RCA}_0$
, plus the arithmetical comprehension scheme, which consists of the universal closures of all formulas of the form
$\mathsf {RCA}_0$
, plus the arithmetical comprehension scheme, which consists of the universal closures of all formulas of the form
where
![]() $\varphi $
is an arithmetical formula in which X is not free. To show that some statement
$\varphi $
is an arithmetical formula in which X is not free. To show that some statement
![]() $\varphi $
implies
$\varphi $
implies
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
, a common strategy is to use
$\mathsf {RCA}_0$
, a common strategy is to use
![]() $\mathsf {RCA}_0 + \varphi $
to show that the ranges of injections exist as sets and appeal to the following well-known lemma.
$\mathsf {RCA}_0 + \varphi $
to show that the ranges of injections exist as sets and appeal to the following well-known lemma.
Lemma 2.1 [Reference Simpson30, Lemma III.1.3].
The following are equivalent over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
-
(1)
 $\mathsf {ACA}_0$
.
$\mathsf {ACA}_0$
. -
(2) If
 $f \colon \mathbb {N} \rightarrow \mathbb {N}$
is an injection, then there is a set X such that
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
is an injection, then there is a set X such that
 $\forall n \, (n \in X \;\leftrightarrow \; \exists s \, (f(s) = n))$
.
$\forall n \, (n \in X \;\leftrightarrow \; \exists s \, (f(s) = n))$
.
Unlike its weak version, the full version of König’s lemma, which states that every infinite finitely branching tree
![]() $T \subseteq \mathbb {N}^{<\mathbb {N}}$
has an infinite path, is equivalent to
$T \subseteq \mathbb {N}^{<\mathbb {N}}$
has an infinite path, is equivalent to
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
(see [Reference Simpson30, Theorem III.7.2]).
$\mathsf {RCA}_0$
(see [Reference Simpson30, Theorem III.7.2]).
The axioms of
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
(for
$\Pi ^1_1\text {-}\mathsf {CA}_0$
(for
![]() $\Pi ^1_1$
comprehension axiom) are those of
$\Pi ^1_1$
comprehension axiom) are those of
![]() $\mathsf {RCA}_0$
, plus the
$\mathsf {RCA}_0$
, plus the
![]() $\Pi ^1_1$
comprehension scheme, which consists of the universal closures of all formulas of the form
$\Pi ^1_1$
comprehension scheme, which consists of the universal closures of all formulas of the form
where
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Pi ^1_1$
formula in which X is not free. To show that some statement
$\Pi ^1_1$
formula in which X is not free. To show that some statement
![]() $\varphi $
implies
$\varphi $
implies
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
over
$\Pi ^1_1\text {-}\mathsf {CA}_0$
over
![]() $\mathsf {RCA}_0$
, a useful tool is to use
$\mathsf {RCA}_0$
, a useful tool is to use
![]() $\mathsf {RCA}_0 + \varphi $
to show that every ill-founded tree has a leftmost path. For functions
$\mathsf {RCA}_0 + \varphi $
to show that every ill-founded tree has a leftmost path. For functions
![]() $f,g \colon \mathbb {N} \rightarrow \mathbb {N}$
, say that g is to the left of f if
$f,g \colon \mathbb {N} \rightarrow \mathbb {N}$
, say that g is to the left of f if
![]() $\exists n \, \bigl (g(n) < f(n) \;\wedge \; \forall i < n \; (g(i) = f(i))\bigr )$
. The leftmost path principle (
$\exists n \, \bigl (g(n) < f(n) \;\wedge \; \forall i < n \; (g(i) = f(i))\bigr )$
. The leftmost path principle (
![]() $\mathsf {LPP}$
) states that for every ill-founded tree
$\mathsf {LPP}$
) states that for every ill-founded tree
![]() $T \subseteq \mathbb {N}^{<\mathbb {N}}$
, there is an infinite path f through T such that no infinite path through T is to the left of f.
$T \subseteq \mathbb {N}^{<\mathbb {N}}$
, there is an infinite path f through T such that no infinite path through T is to the left of f.
Theorem 2.2 [Reference Marcone24, Theorem 6.5].
The following are equivalent over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
-
(1)
 $\Pi ^1_1\text {-}\mathsf {CA}_0$
.
$\Pi ^1_1\text {-}\mathsf {CA}_0$
. -
(2)
 $\mathsf {LPP}$
.
$\mathsf {LPP}$
.
A huge amount of research in reverse mathematics is devoted to understanding the strength of Ramsey’s theorem for pairs and its consequences. For a set
![]() $X \subseteq \mathbb {N}$
, let
$X \subseteq \mathbb {N}$
, let
![]() $[X]^2$
denote the set of two-element subsets of X, which may be encoded as
$[X]^2$
denote the set of two-element subsets of X, which may be encoded as
![]() $[X]^2 = \{\langle x, y \rangle : x, y \in X \;\wedge \; x < y\}$
. A function
$[X]^2 = \{\langle x, y \rangle : x, y \in X \;\wedge \; x < y\}$
. A function
![]() $c \colon [\mathbb {N}]^2 \rightarrow k$
is called a k-coloring of pairs, and an infinite set
$c \colon [\mathbb {N}]^2 \rightarrow k$
is called a k-coloring of pairs, and an infinite set
![]() $H \subseteq \mathbb {N}$
is called homogeneous for a k-coloring of pairs c if c is constant on
$H \subseteq \mathbb {N}$
is called homogeneous for a k-coloring of pairs c if c is constant on
![]() $[H]^2$
. Furthermore, a k-coloring of pairs c is called stable if
$[H]^2$
. Furthermore, a k-coloring of pairs c is called stable if
![]() $\lim _s c(n,s)$
exists for every n. Ramsey’s theorem for pairs and k colors (
$\lim _s c(n,s)$
exists for every n. Ramsey’s theorem for pairs and k colors (
![]() $\mathsf {RT}^2_k$
) states that for every k-coloring of pairs c, there is a set that is homogeneous for c. Stable Ramsey’s theorem for pairs and k colors (
$\mathsf {RT}^2_k$
) states that for every k-coloring of pairs c, there is a set that is homogeneous for c. Stable Ramsey’s theorem for pairs and k colors (
![]() $\mathsf {SRT}^2_k$
) is the restriction of
$\mathsf {SRT}^2_k$
) is the restriction of
![]() $\mathsf {RT}^2_k$
to stable k-colorings of pairs c.
$\mathsf {RT}^2_k$
to stable k-colorings of pairs c.
![]() $\mathsf {RT}^2_{<\infty }$
abbreviates
$\mathsf {RT}^2_{<\infty }$
abbreviates
![]() $\forall k \, \mathsf {RT}^2_k$
and
$\forall k \, \mathsf {RT}^2_k$
and
![]() $\mathsf {SRT}^2_{<\infty }$
abbreviates
$\mathsf {SRT}^2_{<\infty }$
abbreviates
![]() $\forall k \, \mathsf {SRT}^2_k$
. Likewise, a function
$\forall k \, \mathsf {SRT}^2_k$
. Likewise, a function
![]() $c \colon \mathbb {N} \rightarrow k$
is called a k-coloring of singletons, and an infinite
$c \colon \mathbb {N} \rightarrow k$
is called a k-coloring of singletons, and an infinite
![]() $H \subseteq \mathbb {N}$
is called homogeneous for a k-coloring of singletons c if c is constant on H. Ramsey’s theorem for singletons and k colors (
$H \subseteq \mathbb {N}$
is called homogeneous for a k-coloring of singletons c if c is constant on H. Ramsey’s theorem for singletons and k colors (
![]() $\mathsf {RT}^1_k$
) states that for every k-coloring of singletons c, there is a set that is homogeneous for c.
$\mathsf {RT}^1_k$
) states that for every k-coloring of singletons c, there is a set that is homogeneous for c.
![]() $\mathsf {RT}^1_{<\infty }$
abbreviates
$\mathsf {RT}^1_{<\infty }$
abbreviates
![]() $\forall k \, \mathsf {RT}^1_k$
, which we think of as expressing the infinite pigeonhole principle.
$\forall k \, \mathsf {RT}^1_k$
, which we think of as expressing the infinite pigeonhole principle.
![]() $\mathsf {RCA}_0$
proves
$\mathsf {RCA}_0$
proves
![]() $\mathsf {RT}^1_k$
for each fixed standard k, but it does not prove
$\mathsf {RT}^1_k$
for each fixed standard k, but it does not prove
![]() $\mathsf {RT}^1_{<\infty }$
.
$\mathsf {RT}^1_{<\infty }$
.
Of the many combinatorial consequences of
![]() $\mathsf {RT}^2_2$
, we are primarily concerned with the ascending/descending sequence principle (
$\mathsf {RT}^2_2$
, we are primarily concerned with the ascending/descending sequence principle (
![]() $\mathsf {ADS}$
), stating that every countably infinite linear order has either an infinite ascending sequence or an infinite descending sequence, as well as its stable version
$\mathsf {ADS}$
), stating that every countably infinite linear order has either an infinite ascending sequence or an infinite descending sequence, as well as its stable version
![]() $\mathsf {SADS}$
. To be precise, let
$\mathsf {SADS}$
. To be precise, let
![]() $(L, <_L)$
be a linear order. A set
$(L, <_L)$
be a linear order. A set
![]() $S \subseteq L$
is an ascending sequence if
$S \subseteq L$
is an ascending sequence if
![]() $\forall x, y \in S \; (x < y \rightarrow x <_L y)$
, and it is a descending sequence if
$\forall x, y \in S \; (x < y \rightarrow x <_L y)$
, and it is a descending sequence if
![]() $\forall x, y \in S \; (x < y \rightarrow y <_L x)$
. The principle
$\forall x, y \in S \; (x < y \rightarrow y <_L x)$
. The principle
![]() $\mathsf {ADS}$
then states that for every infinite linear order
$\mathsf {ADS}$
then states that for every infinite linear order
![]() $(L, <_L)$
, there is an infinite
$(L, <_L)$
, there is an infinite
![]() $S \subseteq L$
that is either an ascending sequence or a descending sequence. Often it is more convenient to phrase
$S \subseteq L$
that is either an ascending sequence or a descending sequence. Often it is more convenient to phrase
![]() $\mathsf {ADS}$
by stating that for every infinite linear order
$\mathsf {ADS}$
by stating that for every infinite linear order
![]() $(L, <_L)$
, there is an infinite sequence
$(L, <_L)$
, there is an infinite sequence
![]() $\langle x_n : n \in \mathbb {N} \rangle $
of elements of L such that either
$\langle x_n : n \in \mathbb {N} \rangle $
of elements of L such that either
![]() $x_0 <_L x_1 <_L x_2 <_L \cdots $
or
$x_0 <_L x_1 <_L x_2 <_L \cdots $
or
![]() $x_0>_L x_1 >_L x_2 >_L \cdots $
.
$x_0>_L x_1 >_L x_2 >_L \cdots $
.
![]() $\mathsf {RCA}_0$
proves that the two phrasings of
$\mathsf {RCA}_0$
proves that the two phrasings of
![]() $\mathsf {ADS}$
are equivalent because it proves that any sequence
$\mathsf {ADS}$
are equivalent because it proves that any sequence
![]() $x_0, x_1, x_2, \dots $
of distinct elements of
$x_0, x_1, x_2, \dots $
of distinct elements of
![]() $\mathbb {N}$
can be thinned to an
$\mathbb {N}$
can be thinned to an
![]() $<$
-increasing subsequence
$<$
-increasing subsequence
![]() $x_{i_0} < x_{i_1} < x_{i_2} < \cdots $
where the set
$x_{i_0} < x_{i_1} < x_{i_2} < \cdots $
where the set
![]() $\{x_{i_n} : n \in \mathbb {N}\}$
exists. Call a linear order
$\{x_{i_n} : n \in \mathbb {N}\}$
exists. Call a linear order
![]() $(L, <_L)$
stable if every element either has only finitely many predecessors or has only finitely many successors.
$(L, <_L)$
stable if every element either has only finitely many predecessors or has only finitely many successors.
![]() $\mathsf {SADS}$
is the restriction of
$\mathsf {SADS}$
is the restriction of
![]() $\mathsf {ADS}$
to infinite stable linear orders. Closely related to
$\mathsf {ADS}$
to infinite stable linear orders. Closely related to
![]() $\mathsf {ADS}$
is the chain/antichain principle (
$\mathsf {ADS}$
is the chain/antichain principle (
![]() $\mathsf {CAC}$
), which states that every infinite partial order has either an infinite chain or an infinite antichain. Figure 1 summarizes the relationships among several of the systems and principles mentioned thus far.
$\mathsf {CAC}$
), which states that every infinite partial order has either an infinite chain or an infinite antichain. Figure 1 summarizes the relationships among several of the systems and principles mentioned thus far.

Figure 1 Selected principles and systems and their implications and non-implications over
![]() $\mathsf {RCA}_0$
. An arrow indicates that the source principle/system implies the target principle/system over
$\mathsf {RCA}_0$
. An arrow indicates that the source principle/system implies the target principle/system over
![]() $\mathsf {RCA}_0$
. No further arrows may be added, except those that may be inferred via transitivity. No arrows reverse. Proofs of these implications and separations may be found in [Reference Chong, Lempp and Yang6, Reference Chong, Slaman and Yang8, Reference Hirschfeldt and Shore16, Reference Hirst17, Reference Lerman, Solomon and Towsner21, Reference Liu22, Reference Patey26, Reference Seetapun and Slaman29, Reference Simpson30].
$\mathsf {RCA}_0$
. No further arrows may be added, except those that may be inferred via transitivity. No arrows reverse. Proofs of these implications and separations may be found in [Reference Chong, Lempp and Yang6, Reference Chong, Slaman and Yang8, Reference Hirschfeldt and Shore16, Reference Hirst17, Reference Lerman, Solomon and Towsner21, Reference Liu22, Reference Patey26, Reference Seetapun and Slaman29, Reference Simpson30].
Finally, we recall the induction schemes and their cousins, to which we collectively refer as the first-order schemes.
-
• The induction axiom for
 $\varphi $
is the universal closure of the formula
$\varphi $
is the universal closure of the formula  $$ \begin{align*} \bigl(\varphi(0) \;\wedge\; \forall n \, (\varphi(n) \;\rightarrow\; \varphi(n+1))\bigr) \;\rightarrow\; \forall n \, \varphi(n). \end{align*} $$
$$ \begin{align*} \bigl(\varphi(0) \;\wedge\; \forall n \, (\varphi(n) \;\rightarrow\; \varphi(n+1))\bigr) \;\rightarrow\; \forall n \, \varphi(n). \end{align*} $$
-
• The least element principle for
 $\varphi $
is the universal closure of the formula
$\varphi $
is the universal closure of the formula  $$ \begin{align*} \exists n \, \varphi(n) \;\rightarrow\; \exists n \, \bigl(\varphi(n) \;\wedge\; \forall m < n \; \neg\varphi(m)\bigr). \end{align*} $$
$$ \begin{align*} \exists n \, \varphi(n) \;\rightarrow\; \exists n \, \bigl(\varphi(n) \;\wedge\; \forall m < n \; \neg\varphi(m)\bigr). \end{align*} $$
-
• The bounded comprehension axiom for
 $\varphi $
is the universal closure of the formula where X is not free in
$\varphi $
is the universal closure of the formula where X is not free in $$ \begin{align*} \forall b \, \exists X \, \forall n \, \bigl(n \in X \;\leftrightarrow\; (n < b \;\wedge\; \varphi(n))\bigr), \end{align*} $$
$$ \begin{align*} \forall b \, \exists X \, \forall n \, \bigl(n \in X \;\leftrightarrow\; (n < b \;\wedge\; \varphi(n))\bigr), \end{align*} $$
 $\varphi $
.
$\varphi $
.
-
• The bounding (or collection) axiom for
 $\varphi $
is the universal closure of the formula where a and b are not free in
$\varphi $
is the universal closure of the formula where a and b are not free in $$ \begin{align*} \forall a\, \bigl(\forall n < a \; \exists m \; \varphi(n,m) \;\rightarrow\; \exists b \; \forall n < a \; \exists m < b \; \varphi(n,m)\bigr), \end{align*} $$
$$ \begin{align*} \forall a\, \bigl(\forall n < a \; \exists m \; \varphi(n,m) \;\rightarrow\; \exists b \; \forall n < a \; \exists m < b \; \varphi(n,m)\bigr), \end{align*} $$
 $\varphi $
.
$\varphi $
.
For a class of formulas
![]() $\Gamma $
, the
$\Gamma $
, the
![]() $\Gamma $
induction scheme (
$\Gamma $
induction scheme (
![]() $\mathsf {I}\Gamma $
) consists of the induction axioms for all
$\mathsf {I}\Gamma $
) consists of the induction axioms for all
![]() $\varphi \in \Gamma $
, the
$\varphi \in \Gamma $
, the
![]() $\Gamma $
least element principle consists of the least element principles for all
$\Gamma $
least element principle consists of the least element principles for all
![]() $\varphi \in \Gamma $
, the bounded
$\varphi \in \Gamma $
, the bounded
![]() $\Gamma $
comprehension scheme consists of the bounded comprehension axioms for all
$\Gamma $
comprehension scheme consists of the bounded comprehension axioms for all
![]() $\varphi \in \Gamma $
, and the
$\varphi \in \Gamma $
, and the
![]() $\Gamma $
bounding scheme (
$\Gamma $
bounding scheme (
![]() $\mathsf {B}\Gamma $
) consists of the bounding axioms for all
$\mathsf {B}\Gamma $
) consists of the bounding axioms for all
![]() $\varphi \in \Gamma $
. For example,
$\varphi \in \Gamma $
. For example,
![]() $\mathsf {B}\Sigma ^0_{2}$
consists of the bounding axioms for all
$\mathsf {B}\Sigma ^0_{2}$
consists of the bounding axioms for all
![]() $\Sigma ^0_2$
formulas. Beyond
$\Sigma ^0_2$
formulas. Beyond
![]() $\mathsf {RCA}_0$
, we are mostly interested in
$\mathsf {RCA}_0$
, we are mostly interested in
![]() $\mathsf {B}\Sigma ^0_{2}$
and
$\mathsf {B}\Sigma ^0_{2}$
and
![]() $\mathsf {I}\Sigma ^0_{2}$
. The following list summarizes the relationships between the systems and principles of Figure 1 and the first-order schemes.
$\mathsf {I}\Sigma ^0_{2}$
. The following list summarizes the relationships between the systems and principles of Figure 1 and the first-order schemes.
-
•
 $\mathsf {ACA}_0$
proves the induction axiom, least element principle, bounded comprehension axiom, and bounding axiom for every arithmetical formula.
$\mathsf {ACA}_0$
proves the induction axiom, least element principle, bounded comprehension axiom, and bounding axiom for every arithmetical formula. -
• In addition to
 $\mathsf {I}\Sigma ^0_{1}$
,
$\mathsf {I}\Sigma ^0_{1}$
,
 $\mathsf {RCA}_0$
proves
$\mathsf {RCA}_0$
proves
 $\mathsf {I}\Pi ^0_{1}$
, the
$\mathsf {I}\Pi ^0_{1}$
, the
 $\Sigma ^0_1$
least element principle, the
$\Sigma ^0_1$
least element principle, the
 $\Pi ^0_1$
least element principle, the bounded
$\Pi ^0_1$
least element principle, the bounded
 $\Sigma ^0_1$
comprehension scheme, the bounded
$\Sigma ^0_1$
comprehension scheme, the bounded
 $\Pi ^0_1$
comprehension scheme, and
$\Pi ^0_1$
comprehension scheme, and
 $\mathsf {B}\Sigma ^0_{1}$
(see [Reference Hájek and Pudlák14, Section I.2] and [Reference Simpson30], Section II.3).
$\mathsf {B}\Sigma ^0_{1}$
(see [Reference Hájek and Pudlák14, Section I.2] and [Reference Simpson30], Section II.3). -
• Neither
 $\mathsf {RCA}_0$
nor
$\mathsf {RCA}_0$
nor
 $\mathsf {WKL}_0$
proves
$\mathsf {WKL}_0$
proves
 $\mathsf {B}\Sigma ^0_{2}$
(see [Reference Simpson30, Sections IX.1 and IX.2]).
$\mathsf {B}\Sigma ^0_{2}$
(see [Reference Simpson30, Sections IX.1 and IX.2]). -
•
 $\mathsf {RCA}_0$
proves that
$\mathsf {RCA}_0$
proves that
 $\mathsf {B}\Pi ^0_{1}$
,
$\mathsf {B}\Pi ^0_{1}$
,
 $\mathsf {B}\Sigma ^0_{2}$
, and
$\mathsf {B}\Sigma ^0_{2}$
, and
 $\mathsf {RT}^1_{<\infty }$
are equivalent; that
$\mathsf {RT}^1_{<\infty }$
are equivalent; that
 $\mathsf {I}\Sigma ^0_{2}$
,
$\mathsf {I}\Sigma ^0_{2}$
,
 $\mathsf {I}\Pi ^0_{2}$
, the
$\mathsf {I}\Pi ^0_{2}$
, the
 $\Sigma ^0_2$
least element principle, the
$\Sigma ^0_2$
least element principle, the
 $\Pi ^0_2$
least element principle, the bounded
$\Pi ^0_2$
least element principle, the bounded
 $\Sigma ^0_2$
comprehension scheme, and the bounded
$\Sigma ^0_2$
comprehension scheme, and the bounded
 $\Pi ^0_2$
comprehension scheme are all equivalent; and that
$\Pi ^0_2$
comprehension scheme are all equivalent; and that
 $\mathsf {I}\Sigma ^0_{2}$
implies
$\mathsf {I}\Sigma ^0_{2}$
implies
 $\mathsf {B}\Sigma ^0_{2}$
(see [Reference Hájek and Pudlák14, Section I.2], [Reference Hirst17], and [Reference Simpson30, Section II.3]).
$\mathsf {B}\Sigma ^0_{2}$
(see [Reference Hájek and Pudlák14, Section I.2], [Reference Hirst17], and [Reference Simpson30, Section II.3]). -
•
 $\mathsf {SADS}$
and all the systems and principles above it in Figure 1 imply
$\mathsf {SADS}$
and all the systems and principles above it in Figure 1 imply
 $\mathsf {B}\Sigma ^0_{2}$
over
$\mathsf {B}\Sigma ^0_{2}$
over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
. -
•
 $\mathsf {RCA}_0 + \mathsf {RT}^2_2$
does not prove
$\mathsf {RCA}_0 + \mathsf {RT}^2_2$
does not prove
 $\mathsf {I}\Sigma ^0_{2}$
[Reference Chong, Slaman and Yang9].
$\mathsf {I}\Sigma ^0_{2}$
[Reference Chong, Slaman and Yang9].
We emphasize that
![]() $\mathsf {B}\Sigma ^0_{2}$
and
$\mathsf {B}\Sigma ^0_{2}$
and
![]() $\mathsf {RT}^1_{<\infty }$
are equivalent over
$\mathsf {RT}^1_{<\infty }$
are equivalent over
![]() $\mathsf {RCA}_0$
because we use this equivalence often and without special mention.
$\mathsf {RCA}_0$
because we use this equivalence often and without special mention.
3 From one principle to many
We begin studying the Rival–Sands theorem for partial orders from the perspective of reverse mathematics. Typically we use
![]() $\omega $
to denote the order-type of
$\omega $
to denote the order-type of
![]() $(\mathbb {N}, <)$
, use
$(\mathbb {N}, <)$
, use
![]() $\omega ^*$
to denote the order-type of its reverse, and use
$\omega ^*$
to denote the order-type of its reverse, and use
![]() $\zeta $
to denote the order-type
$\zeta $
to denote the order-type
![]() $\omega ^* + \omega $
of the integers. In some places we may write
$\omega ^* + \omega $
of the integers. In some places we may write
![]() $<_{\mathbb {N}}$
,
$<_{\mathbb {N}}$
,
![]() $\leq _{\mathbb {N}}$
, etc. instead of
$\leq _{\mathbb {N}}$
, etc. instead of
![]() $<$
,
$<$
,
![]() $\leq $
, etc. to help disambiguate several orders under discussion.
$\leq $
, etc. to help disambiguate several orders under discussion.
Definition 3.1. Let
![]() $(P, <_P)$
be a partial order.
$(P, <_P)$
be a partial order.
-
• Elements
 $p, q \in P$
are comparable (written
$p, q \in P$
are comparable (written
 $p \lessgtr _P q$
) if either
$p \lessgtr _P q$
) if either
 $p \leq _P q$
or
$p \leq _P q$
or
 $q \leq _P p$
. If p and q are not comparable, then they are incomparable (written
$q \leq _P p$
. If p and q are not comparable, then they are incomparable (written
 $p \mid _P q$
).
$p \mid _P q$
). -
• A chain in P is a set
 $C \subseteq P$
of pairwise comparable elements.
$C \subseteq P$
of pairwise comparable elements. -
• An antichain in P is a set
 $X \subseteq P$
of pairwise incomparable elements.
$X \subseteq P$
of pairwise incomparable elements. -
• P has width
 $\leq \! k$
if every antichain in P has at most k elements. P has width k if it has width
$\leq \! k$
if every antichain in P has at most k elements. P has width k if it has width
 $\leq \! k$
but not width
$\leq \! k$
but not width
 $\leq \! k-1$
. P has finite width if P has width
$\leq \! k-1$
. P has finite width if P has width
 $\leq \! k$
for some k.
$\leq \! k$
for some k. -
• P has height
 $\leq \! k$
if every chain in P has at most k elements. P has height k if it has height
$\leq \! k$
if every chain in P has at most k elements. P has height k if it has height
 $\leq \! k$
but not height
$\leq \! k$
but not height
 $\leq \! k-1$
. P has finite height if P has height
$\leq \! k-1$
. P has finite height if P has height
 $\leq \! k$
for some k.
$\leq \! k$
for some k.
We use the homogeneous terminology from Ramsey’s theorem to describe chains that are as in the conclusion to the Rival–Sands theorem for partial orders.
Definition 3.2. Let
![]() $(P, <_P)$
be a partial order. An infinite chain
$(P, <_P)$
be a partial order. An infinite chain
![]() $C \subseteq P$
is:
$C \subseteq P$
is:
-
•
 $(0,\infty )$
-homogeneous for P if every
$(0,\infty )$
-homogeneous for P if every
 $p \in P$
is either comparable with no element of C or is comparable with infinitely many elements of C;
$p \in P$
is either comparable with no element of C or is comparable with infinitely many elements of C; -
•
 $(0,\mathrm {cof})$
-homogeneous for P if every
$(0,\mathrm {cof})$
-homogeneous for P if every
 $p \in P$
is either comparable with no element of C or is comparable with cofinitely many elements of C.
$p \in P$
is either comparable with no element of C or is comparable with cofinitely many elements of C.
Every infinite subset of a
![]() $(0,\mathrm {cof})$
-homogeneous chain in a partial order is also
$(0,\mathrm {cof})$
-homogeneous chain in a partial order is also
![]() $(0,\mathrm {cof})$
-homogeneous, but an infinite subset of a
$(0,\mathrm {cof})$
-homogeneous, but an infinite subset of a
![]() $(0,\infty )$
-homogeneous chain need not be
$(0,\infty )$
-homogeneous chain need not be
![]() $(0,\infty )$
-homogeneous. Rival and Sands observed that if C is a chain of order-type
$(0,\infty )$
-homogeneous. Rival and Sands observed that if C is a chain of order-type
![]() $\zeta $
in a partial order
$\zeta $
in a partial order
![]() $(P, <_P)$
, then C is automatically
$(P, <_P)$
, then C is automatically
![]() $(0,\infty )$
-homogeneous for P. To wit, if
$(0,\infty )$
-homogeneous for P. To wit, if
![]() $p \in P$
is comparable with some
$p \in P$
is comparable with some
![]() $q \in C$
, then either
$q \in C$
, then either
![]() $p \leq _P q$
and hence p is below infinitely many elements of C, or
$p \leq _P q$
and hence p is below infinitely many elements of C, or
![]() $p \geq _P q$
and hence p is above infinitely many elements of C. Similarly, if C is a
$p \geq _P q$
and hence p is above infinitely many elements of C. Similarly, if C is a
![]() $(0,\infty )$
-homogeneous chain of order-type either
$(0,\infty )$
-homogeneous chain of order-type either
![]() $\omega $
or
$\omega $
or
![]() $\omega ^*$
, then C is automatically
$\omega ^*$
, then C is automatically
![]() $(0,\mathrm {cof})$
-homogeneous. For example, if C has order-type
$(0,\mathrm {cof})$
-homogeneous. For example, if C has order-type
![]() $\omega $
and
$\omega $
and
![]() $p \in P$
is comparable with infinitely many elements of C, then either p is above all elements of C, or p is below some element of C and therefore below cofinitely many elements of C.
$p \in P$
is comparable with infinitely many elements of C, then either p is above all elements of C, or p is below some element of C and therefore below cofinitely many elements of C.
We also apply the
![]() $(0,\infty )$
-homogeneous and
$(0,\infty )$
-homogeneous and
![]() $(0,\mathrm {cof})$
-homogeneous terminology to sequences. An infinite sequence
$(0,\mathrm {cof})$
-homogeneous terminology to sequences. An infinite sequence
![]() $\langle x_n : n \in \mathbb {N} \rangle $
of distinct elements in a partial order
$\langle x_n : n \in \mathbb {N} \rangle $
of distinct elements in a partial order
![]() $(P, <_P)$
is
$(P, <_P)$
is
![]() $(0,\infty )$
-homogeneous if every
$(0,\infty )$
-homogeneous if every
![]() $p \in P$
is either comparable with
$p \in P$
is either comparable with
![]() $x_n$
for no n or is comparable with
$x_n$
for no n or is comparable with
![]() $x_n$
for infinitely many n; and it is
$x_n$
for infinitely many n; and it is
![]() $(0,\mathrm {cof})$
-homogeneous if every
$(0,\mathrm {cof})$
-homogeneous if every
![]() $p \in P$
is either comparable with
$p \in P$
is either comparable with
![]() $x_n$
for no n or is comparable with
$x_n$
for no n or is comparable with
![]() $x_n$
for cofinitely many n. As with chains of order-type
$x_n$
for cofinitely many n. As with chains of order-type
![]() $\omega $
and
$\omega $
and
![]() $\omega ^*$
, an infinite sequence that is
$\omega ^*$
, an infinite sequence that is
![]() $(0,\infty )$
-homogeneous and either ascending or descending is automatically
$(0,\infty )$
-homogeneous and either ascending or descending is automatically
![]() $(0,\mathrm {cof})$
-homogeneous, and therefore all of its infinite subsequences are
$(0,\mathrm {cof})$
-homogeneous, and therefore all of its infinite subsequences are
![]() $(0,\mathrm {cof})$
-homogeneous as well.
$(0,\mathrm {cof})$
-homogeneous as well.
We introduce several formulations of the Rival–Sands theorem for partial orders.
Definition 3.3.
-
•
 $\mathsf {RSpo}_k$
is the statement “Every infinite partial order of width
$\mathsf {RSpo}_k$
is the statement “Every infinite partial order of width
 $\leq \! k$
has a
$\leq \! k$
has a
 $(0, \infty )$
-homogeneous chain.”
$(0, \infty )$
-homogeneous chain.” -
•
 $\mathsf {RSpo}_{<\infty }$
abbreviates
$\mathsf {RSpo}_{<\infty }$
abbreviates
 $\forall k \, \mathsf {RSpo}_k$
.
$\forall k \, \mathsf {RSpo}_k$
. -
•
 $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
is the statement “Every infinite partial order of width
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
is the statement “Every infinite partial order of width
 $\leq \! k$
has a
$\leq \! k$
has a
 $(0, \mathrm {cof})$
-homogeneous chain.”
$(0, \mathrm {cof})$
-homogeneous chain.” -
•
 $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
abbreviates
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
abbreviates
 $\forall k \, (0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
.
$\forall k \, (0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
.
Immediately,
![]() $\mathsf {RCA}_0 \vdash \forall k\, \bigl ((0,\mathrm {cof})\text {-}\mathsf {RSpo}_k \rightarrow \mathsf {RSpo}_k\bigr )$
and therefore
$\mathsf {RCA}_0 \vdash \forall k\, \bigl ((0,\mathrm {cof})\text {-}\mathsf {RSpo}_k \rightarrow \mathsf {RSpo}_k\bigr )$
and therefore
![]() $\mathsf {RCA}_0 \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty } \rightarrow \mathsf {RSpo}_{<\infty }$
. Also, Proposition 6.5 shows that for every
$\mathsf {RCA}_0 \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty } \rightarrow \mathsf {RSpo}_{<\infty }$
. Also, Proposition 6.5 shows that for every
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
is equivalent to the statement “Every infinite partial order of width
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
is equivalent to the statement “Every infinite partial order of width
![]() $\leq \! k$
has a
$\leq \! k$
has a
![]() $(0,\infty )$
-homogeneous chain of order-type either
$(0,\infty )$
-homogeneous chain of order-type either
![]() $\omega $
or
$\omega $
or
![]() $\omega ^*$
.”
$\omega ^*$
.”
When working with partial orders of finite width, it often helps to decompose the partial order into a finite union of chains.
Definition 3.4. A k-chain decomposition of a partial order
![]() $(P, <_P)$
is a collection of k chains
$(P, <_P)$
is a collection of k chains
![]() $C_0, C_1, \dots , C_{k-1} \subseteq P$
where
$C_0, C_1, \dots , C_{k-1} \subseteq P$
where
![]() $P = \bigcup _{i < k} C_i$
. If P has a k-chain decomposition, then it is called k-chain decomposable.
$P = \bigcup _{i < k} C_i$
. If P has a k-chain decomposition, then it is called k-chain decomposable.
We emphasize that if a partial order P is assumed to be k-chain decomposable, then P comes along with a k-chain decomposition. Of course, we may always assume that the chains of a chain decomposition are pairwise disjoint.
Recall now Dilworth’s theorem, which in this terminology states that for every k, every partial order of width
![]() $\leq \! k$
is k-chain decomposable. Hirst [Reference Hirst17] shows that Dilworth’s theorem for countable partial orders is equivalent to
$\leq \! k$
is k-chain decomposable. Hirst [Reference Hirst17] shows that Dilworth’s theorem for countable partial orders is equivalent to
![]() $\mathsf {WKL}_0$
over
$\mathsf {WKL}_0$
over
![]() $\mathsf {RCA}_0$
. He also shows that Dilworth’s theorem remains equivalent to
$\mathsf {RCA}_0$
. He also shows that Dilworth’s theorem remains equivalent to
![]() $\mathsf {WKL}_0$
even when restricted to partial orders of width
$\mathsf {WKL}_0$
even when restricted to partial orders of width
![]() $2$
. It follows that there is a recursive partial order of width
$2$
. It follows that there is a recursive partial order of width
![]() $2$
that cannot be decomposed into
$2$
that cannot be decomposed into
![]() $2$
recursive chains. Thus Dilworth’s theorem is not available when working in
$2$
recursive chains. Thus Dilworth’s theorem is not available when working in
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
because
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
because
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \nvdash \mathsf {WKL}_0$
. However, for our purposes it is not necessary to decompose a partial order of finite width into the optimal number of chains—any decomposition into finitely many chains will do. Thus we replace Dilworth’s theorem by Kierstead’s effective analog, which states that every recursive partial order of width
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \nvdash \mathsf {WKL}_0$
. However, for our purposes it is not necessary to decompose a partial order of finite width into the optimal number of chains—any decomposition into finitely many chains will do. Thus we replace Dilworth’s theorem by Kierstead’s effective analog, which states that every recursive partial order of width
![]() $\leq \! k$
can be decomposed into at most
$\leq \! k$
can be decomposed into at most
![]() $(5^k - 1)/4$
recursive chains [Reference Kierstead18]. Nowadays much better sub-exponential bounds are known for the number of recursive chains into which a recursive partial order of finite width can be decomposed [Reference Bosek and Krawczyk3].
$(5^k - 1)/4$
recursive chains [Reference Kierstead18]. Nowadays much better sub-exponential bounds are known for the number of recursive chains into which a recursive partial order of finite width can be decomposed [Reference Bosek and Krawczyk3].
Let
![]() $(P, <_P)$
be a partial order of width
$(P, <_P)$
be a partial order of width
![]() $\leq \! k$
. Kierstead’s proof is phrased as an induction on k. By unwinding the induction, the proof can be viewed as an on-line algorithm computing a sequence of partial orders
$\leq \! k$
. Kierstead’s proof is phrased as an induction on k. By unwinding the induction, the proof can be viewed as an on-line algorithm computing a sequence of partial orders
![]() $(P, <_P) = (P_0, <_{P_0}), (P_1, <_{P_1}), \dots , (P_{k-2}, <_{P_{k-2}})$
, where
$(P, <_P) = (P_0, <_{P_0}), (P_1, <_{P_1}), \dots , (P_{k-2}, <_{P_{k-2}})$
, where
![]() $P_i$
has width
$P_i$
has width
![]() $\leq \! k-i$
for each
$\leq \! k-i$
for each
![]() $i \leq k-2$
, together with a
$i \leq k-2$
, together with a
![]() $(5^{k-i} - 1)/4$
-chain decomposition of
$(5^{k-i} - 1)/4$
-chain decomposition of
![]() $(P_i, <_{P_i})$
for each
$(P_i, <_{P_i})$
for each
![]() $i \leq k-2$
. Kierstead himself comments along these lines following the proof of [Reference Kierstead18, Theorem 1.10]. With this view, it is possible to verify that Kierstead’s theorem is provable in
$i \leq k-2$
. Kierstead himself comments along these lines following the proof of [Reference Kierstead18, Theorem 1.10]. With this view, it is possible to verify that Kierstead’s theorem is provable in
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Theorem 3.5 (essentially Kierstead [Reference Kierstead18]).
![]() $\mathsf {RCA}_0$
proves the statement “For every k, every partial order of width
$\mathsf {RCA}_0$
proves the statement “For every k, every partial order of width
![]() $\leq \! k$
is
$\leq \! k$
is
![]() $(5^k - 1)/4$
-chain decomposable.”
$(5^k - 1)/4$
-chain decomposable.”
For notational ease, we work with
![]() $5^k$
-chain decompositions in place of
$5^k$
-chain decompositions in place of
![]() $(5^k - 1)/4$
-chain decompositions. Again, for our purposes, any primitive recursive bound suffices.
$(5^k - 1)/4$
-chain decompositions. Again, for our purposes, any primitive recursive bound suffices.
For completeness, we mention that there is a dual version of Dilworth’s theorem, due to Mirsky, which states that every partial order of height
![]() $\leq \! k$
can be decomposed into a union of k antichains. Hirst proved that Mirsky’s theorem for countable partial orders is equivalent to
$\leq \! k$
can be decomposed into a union of k antichains. Hirst proved that Mirsky’s theorem for countable partial orders is equivalent to
![]() $\mathsf {WKL}_0$
over
$\mathsf {WKL}_0$
over
![]() $\mathsf {RCA}_0$
[Reference Hirst17]. There is also an effective analog of Mirsky’s theorem in the spirit of Theorem 3.5 [Reference Kierstead19].
$\mathsf {RCA}_0$
[Reference Hirst17]. There is also an effective analog of Mirsky’s theorem in the spirit of Theorem 3.5 [Reference Kierstead19].
We now formalize versions of
![]() $\mathsf {RSpo}$
with the assumption “width
$\mathsf {RSpo}$
with the assumption “width
![]() $\leq \! k$
” replaced by “k-chain decomposable.”
$\leq \! k$
” replaced by “k-chain decomposable.”
Definition 3.6.
-
•
 $\mathsf {RSpo}^{\mathsf {CD}}_k$
is the statement “Every infinite k-chain decomposable partial order has a
$\mathsf {RSpo}^{\mathsf {CD}}_k$
is the statement “Every infinite k-chain decomposable partial order has a
 $(0, \infty )$
-homogeneous chain.”
$(0, \infty )$
-homogeneous chain.” -
•
 $\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
abbreviates
$\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
abbreviates
 $\forall k \, \mathsf {RSpo}^{\mathsf {CD}}_k$
.
$\forall k \, \mathsf {RSpo}^{\mathsf {CD}}_k$
. -
•
 $(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_k$
is the statement “Every infinite k-chain decomposable partial order has a
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_k$
is the statement “Every infinite k-chain decomposable partial order has a
 $(0, \mathrm {cof})$
-homogeneous chain.”
$(0, \mathrm {cof})$
-homogeneous chain.” -
•
 $(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
abbreviates
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
abbreviates
 $\forall k \, (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_k$
.
$\forall k \, (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_k$
.
We have that
![]() $\mathsf {RCA}_0 \vdash \forall k \, \bigl ((\mathsf {RSpo}^{\mathsf {CD}}_{5^k} \rightarrow \mathsf {RSpo}_k) \;\wedge \; (\mathsf {RSpo}_k \rightarrow \mathsf {RSpo}^{\mathsf {CD}}_k)\bigr )$
and analogously for the
$\mathsf {RCA}_0 \vdash \forall k \, \bigl ((\mathsf {RSpo}^{\mathsf {CD}}_{5^k} \rightarrow \mathsf {RSpo}_k) \;\wedge \; (\mathsf {RSpo}_k \rightarrow \mathsf {RSpo}^{\mathsf {CD}}_k)\bigr )$
and analogously for the
![]() $(0,\mathrm {cof})$
-homogeneous versions by Theorem 3.5 and the fact that k-chain decomposable partial orders have width
$(0,\mathrm {cof})$
-homogeneous versions by Theorem 3.5 and the fact that k-chain decomposable partial orders have width
![]() $\leq \! k$
. It follows that
$\leq \! k$
. It follows that
![]() $\mathsf {RCA}_0 \vdash \mathsf {RSpo}_{<\infty } \leftrightarrow \mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
and that
$\mathsf {RCA}_0 \vdash \mathsf {RSpo}_{<\infty } \leftrightarrow \mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
and that
![]() $\mathsf {RCA}_0 \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty } \leftrightarrow (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
. Additionally,
$\mathsf {RCA}_0 \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty } \leftrightarrow (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
. Additionally,
![]() $\mathsf {WKL}_0 \vdash \forall k \, (\mathsf {RSpo}_k \leftrightarrow \mathsf {RSpo}^{\mathsf {CD}}_k)$
and analogously for the
$\mathsf {WKL}_0 \vdash \forall k \, (\mathsf {RSpo}_k \leftrightarrow \mathsf {RSpo}^{\mathsf {CD}}_k)$
and analogously for the
![]() $(0,\mathrm {cof})$
-homogeneous versions because
$(0,\mathrm {cof})$
-homogeneous versions because
![]() $\mathsf {WKL}_0$
proves Dilworth’s theorem.
$\mathsf {WKL}_0$
proves Dilworth’s theorem.
We conclude this section with a few other useful applications of Theorem 3.5. If
![]() $(P, <_P)$
is an infinite partial order of width
$(P, <_P)$
is an infinite partial order of width
![]() $\leq \! k$
, then
$\leq \! k$
, then
![]() $\mathsf {CAC}$
implies that P contains an infinite chain because P does not contain an infinite antichain. However, we may argue more effectively by instead applying Theorem 3.5 to P to obtain a
$\mathsf {CAC}$
implies that P contains an infinite chain because P does not contain an infinite antichain. However, we may argue more effectively by instead applying Theorem 3.5 to P to obtain a
![]() $5^k$
-chain decomposition of P and then by applying the pigeonhole principle to conclude that one of these chains must be infinite. Dually,
$5^k$
-chain decomposition of P and then by applying the pigeonhole principle to conclude that one of these chains must be infinite. Dually,
![]() $\mathsf {CAC}$
implies that an infinite partial order of height
$\mathsf {CAC}$
implies that an infinite partial order of height
![]() $\leq \! k$
contains an infinite antichain, and this fact can be effectivized as well. We show that these special cases of
$\leq \! k$
contains an infinite antichain, and this fact can be effectivized as well. We show that these special cases of
![]() $\mathsf {CAC}$
are provable in
$\mathsf {CAC}$
are provable in
![]() $\mathsf {RCA}_0$
for each fixed k and are equivalent to
$\mathsf {RCA}_0$
for each fixed k and are equivalent to
![]() $\mathsf {B}\Sigma ^0_{2}$
over
$\mathsf {B}\Sigma ^0_{2}$
over
![]() $\mathsf {RCA}_0$
for arbitrary k.
$\mathsf {RCA}_0$
for arbitrary k.
Definition 3.7.
-
•
 $\mathsf {CC}_k$
is the statement “Every infinite partial order of width
$\mathsf {CC}_k$
is the statement “Every infinite partial order of width
 $\leq \! k$
has an infinite chain.”
$\leq \! k$
has an infinite chain.” -
•
 $\mathsf {CC}_{<\infty }$
abbreviates
$\mathsf {CC}_{<\infty }$
abbreviates
 $\forall k \, \mathsf {CC}_k$
.
$\forall k \, \mathsf {CC}_k$
. -
•
 $\mathsf {CA}_k$
is the statement “Every infinite partial order of height
$\mathsf {CA}_k$
is the statement “Every infinite partial order of height
 $\leq \! k$
has an infinite antichain.”
$\leq \! k$
has an infinite antichain.” -
•
 $\mathsf {CA}_{<\infty }$
abbreviates
$\mathsf {CA}_{<\infty }$
abbreviates
 $\forall k \, \mathsf {CA}_k$
.
$\forall k \, \mathsf {CA}_k$
.
Proposition 3.8.
-
(1) For each fixed standard k,
 $\mathsf {RCA}_0 \vdash \mathsf {CC}_k,$
and
$\mathsf {RCA}_0 \vdash \mathsf {CC}_k,$
and
 $\mathsf {RCA}_0 \vdash \mathsf {CA}_k$
.
$\mathsf {RCA}_0 \vdash \mathsf {CA}_k$
. -
(2)
 $\mathsf {CC}_{<\infty }$
,
$\mathsf {CC}_{<\infty }$
,
 $\mathsf {CA}_{<\infty }$
, and
$\mathsf {CA}_{<\infty }$
, and
 $\mathsf {B}\Sigma ^0_{2}$
are pairwise equivalent over
$\mathsf {B}\Sigma ^0_{2}$
are pairwise equivalent over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Proof For
![]() $\mathsf {RCA}_0 \vdash \mathsf {CC}_k$
, let
$\mathsf {RCA}_0 \vdash \mathsf {CC}_k$
, let
![]() $(P, <_P)$
be an infinite partial order of width
$(P, <_P)$
be an infinite partial order of width
![]() $\leq \! k$
. By Theorem 3.5, P has a
$\leq \! k$
. By Theorem 3.5, P has a
![]() $5^k$
-chain decomposition, and at least one of these chains is infinite by
$5^k$
-chain decomposition, and at least one of these chains is infinite by
![]() $\mathsf {RT}^1_{5^k}$
. Thus P has an infinite chain. The proof that
$\mathsf {RT}^1_{5^k}$
. Thus P has an infinite chain. The proof that
![]() $\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_{2} \vdash \mathsf {CC}_{<\infty }$
is the same, except we must use
$\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_{2} \vdash \mathsf {CC}_{<\infty }$
is the same, except we must use
![]() $\mathsf {RT}^1_{<\infty }$
instead of
$\mathsf {RT}^1_{<\infty }$
instead of
![]() $\mathsf {RT}^1_{5^k}$
because now k is not fixed in advance.
$\mathsf {RT}^1_{5^k}$
because now k is not fixed in advance.
For
![]() $\mathsf {RCA}_0 \vdash \mathsf {CA}_k$
, we give a direct proof instead of appealing to an effective analog of Mirsky’s theorem. Let
$\mathsf {RCA}_0 \vdash \mathsf {CA}_k$
, we give a direct proof instead of appealing to an effective analog of Mirsky’s theorem. Let
![]() $(P, <_P)$
be an infinite partial order of height
$(P, <_P)$
be an infinite partial order of height
![]() $\leq \! k$
. Define a coloring
$\leq \! k$
. Define a coloring
![]() $c \colon P \rightarrow k^2$
by
$c \colon P \rightarrow k^2$
by
![]() $c(p) = \langle x, y \rangle $
, where x is the greatest size of a
$c(p) = \langle x, y \rangle $
, where x is the greatest size of a
![]() $<_P$
-chain in
$<_P$
-chain in
![]() $\{q <_{\mathbb {N}} p : q <_P p\}$
and y is the greatest size of a
$\{q <_{\mathbb {N}} p : q <_P p\}$
and y is the greatest size of a
![]() $<_P$
-chain in
$<_P$
-chain in
![]() $\{q <_{\mathbb {N}} p : p <_P q\}$
. Both x and y are less than k because P has height
$\{q <_{\mathbb {N}} p : p <_P q\}$
. Both x and y are less than k because P has height
![]() $\leq \! k$
. By
$\leq \! k$
. By
![]() $\mathsf {RT}^1_{k^2}$
, let
$\mathsf {RT}^1_{k^2}$
, let
![]() $H \subseteq P$
be an infinite set that is homogeneous for c. We claim that H is an antichain. Suppose for a contradiction that
$H \subseteq P$
be an infinite set that is homogeneous for c. We claim that H is an antichain. Suppose for a contradiction that
![]() $a, b \in H$
and
$a, b \in H$
and
![]() $a <_P b$
. If
$a <_P b$
. If
![]() $a <_{\mathbb {N}} b$
and
$a <_{\mathbb {N}} b$
and
![]() $q_0 <_P q_1 <_P \cdots <_P q_{n-1}$
is a chain in
$q_0 <_P q_1 <_P \cdots <_P q_{n-1}$
is a chain in
![]() $\{q <_{\mathbb {N}} a : q <_P a\}$
, then
$\{q <_{\mathbb {N}} a : q <_P a\}$
, then
![]() $q_0 <_P q_1 <_P \cdots <_P q_{n-1} <_P a$
is a chain in
$q_0 <_P q_1 <_P \cdots <_P q_{n-1} <_P a$
is a chain in
![]() $\{q <_{\mathbb {N}} b : q <_P b\}$
. This means that if x is the maximum size of a chain in
$\{q <_{\mathbb {N}} b : q <_P b\}$
. This means that if x is the maximum size of a chain in
![]() $\{q <_{\mathbb {N}} a : q <_P a\}$
, then the maximum size of a chain in
$\{q <_{\mathbb {N}} a : q <_P a\}$
, then the maximum size of a chain in
![]() $\{q <_{\mathbb {N}} b : q <_P b\}$
is at least
$\{q <_{\mathbb {N}} b : q <_P b\}$
is at least
![]() $x+1$
. So
$x+1$
. So
![]() $c(a) \neq c(b)$
, contradicting that H is homogeneous. Similar reasoning shows that if
$c(a) \neq c(b)$
, contradicting that H is homogeneous. Similar reasoning shows that if
![]() $b <_{\mathbb {N}} a$
, then
$b <_{\mathbb {N}} a$
, then
![]() $c(a) \neq c(b)$
as well. Therefore H is an infinite antichain in P. The proof that
$c(a) \neq c(b)$
as well. Therefore H is an infinite antichain in P. The proof that
![]() $\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_{2} \vdash \mathsf {CA}_{<\infty }$
is the same, except we must use
$\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_{2} \vdash \mathsf {CA}_{<\infty }$
is the same, except we must use
![]() $\mathsf {RT}^1_{<\infty }$
instead of
$\mathsf {RT}^1_{<\infty }$
instead of
![]() $\mathsf {RT}^1_{k^2}$
because now k is not fixed in advance.
$\mathsf {RT}^1_{k^2}$
because now k is not fixed in advance.
For
![]() $\mathsf {RCA}_0 + \mathsf {CC}_{<\infty } \vdash \mathsf {B}\Sigma ^0_{2}$
, let
$\mathsf {RCA}_0 + \mathsf {CC}_{<\infty } \vdash \mathsf {B}\Sigma ^0_{2}$
, let
![]() $c \colon \mathbb {N} \rightarrow k$
be a k-coloring, and define a partial order
$c \colon \mathbb {N} \rightarrow k$
be a k-coloring, and define a partial order
![]() $(P, <_P)$
with
$(P, <_P)$
with
![]() $P = \mathbb {N}$
by setting
$P = \mathbb {N}$
by setting
![]() $p <_P q$
if and only if
$p <_P q$
if and only if
![]() $p <_{\mathbb {N}} q$
and
$p <_{\mathbb {N}} q$
and
![]() $c(p) = c(q)$
. The partial order P has width
$c(p) = c(q)$
. The partial order P has width
![]() $\leq \! k$
, so by
$\leq \! k$
, so by
![]() $\mathsf {CC}_{<\infty }$
it has an infinite chain H. By the definition of
$\mathsf {CC}_{<\infty }$
it has an infinite chain H. By the definition of
![]() $<_P$
, H must be homogeneous for c. Therefore
$<_P$
, H must be homogeneous for c. Therefore
![]() $\mathsf {RT}^1_{<\infty }$
holds.
$\mathsf {RT}^1_{<\infty }$
holds.
For
![]() $\mathsf {RCA}_0 + \mathsf {CA}_{<\infty } \vdash \mathsf {B}\Sigma ^0_{2}$
, let
$\mathsf {RCA}_0 + \mathsf {CA}_{<\infty } \vdash \mathsf {B}\Sigma ^0_{2}$
, let
![]() $c \colon \mathbb {N} \rightarrow k$
be a k-coloring, and define a partial order
$c \colon \mathbb {N} \rightarrow k$
be a k-coloring, and define a partial order
![]() $(P, <_P)$
with
$(P, <_P)$
with
![]() $P = \mathbb {N}$
by setting
$P = \mathbb {N}$
by setting
![]() $p <_P q$
if and only if
$p <_P q$
if and only if
![]() $c(p) < c(q)$
. The partial order P has height
$c(p) < c(q)$
. The partial order P has height
![]() $\leq \! k$
, so by
$\leq \! k$
, so by
![]() $\mathsf {CA}_{<\infty }$
it has an infinite antichain H. By the definition of
$\mathsf {CA}_{<\infty }$
it has an infinite antichain H. By the definition of
![]() $<_P$
, H must be homogeneous for c. Therefore
$<_P$
, H must be homogeneous for c. Therefore
![]() $\mathsf {RT}^1_{<\infty }$
holds.
$\mathsf {RT}^1_{<\infty }$
holds.
We now show that
![]() $\mathsf {ADS}$
is equivalent to the statement “Every infinite partial order of finite width contains either an infinite ascending sequence or an infinite descending sequence.”
$\mathsf {ADS}$
is equivalent to the statement “Every infinite partial order of finite width contains either an infinite ascending sequence or an infinite descending sequence.”
Proposition 3.9. The following are equivalent over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
-
(1)
 $\mathsf {ADS}$
.
$\mathsf {ADS}$
. -
(2) Every infinite partial order of finite width contains either an infinite ascending sequence or an infinite descending sequence.
-
(3) For each fixed standard
 $k \geq 1$
, the statement “Every infinite partial order of width
$k \geq 1$
, the statement “Every infinite partial order of width
 $\leq \! k$
contains either an infinite ascending sequence or an infinite descending sequence.”
$\leq \! k$
contains either an infinite ascending sequence or an infinite descending sequence.”
Proof For (1)
![]() $\Rightarrow $
(2), let
$\Rightarrow $
(2), let
![]() $(P, <_P)$
be an infinite partial order of width
$(P, <_P)$
be an infinite partial order of width
![]() $\leq \! k$
for some k. Using the fact that
$\leq \! k$
for some k. Using the fact that
![]() $\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {B}\Sigma ^0_{2}$
, we may appeal to Proposition 3.8 item (2) and apply
$\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {B}\Sigma ^0_{2}$
, we may appeal to Proposition 3.8 item (2) and apply
![]() $\mathsf {CC}_{<\infty }$
to P to obtain an infinite chain C in P. Now apply
$\mathsf {CC}_{<\infty }$
to P to obtain an infinite chain C in P. Now apply
![]() $\mathsf {ADS}$
to C to obtain either an infinite ascending sequence in C or an infinite descending sequence in C.
$\mathsf {ADS}$
to C to obtain either an infinite ascending sequence in C or an infinite descending sequence in C.
The implications (2)
![]() $\Rightarrow $
(3) and (3)
$\Rightarrow $
(3) and (3)
![]() $\Rightarrow $
(1) are immediate because every partial order of width
$\Rightarrow $
(1) are immediate because every partial order of width
![]() $\leq \! k$
has finite width, and every infinite linear order is an infinite partial order of width
$\leq \! k$
has finite width, and every infinite linear order is an infinite partial order of width
![]() $1$
.
$1$
.
4 First proofs of
 $\mathsf {RSpo}_{<\infty }$
and
$\mathsf {RSpo}_{<\infty }$
and
 $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
We give a proof of
![]() $\mathsf {RSpo}_{<\infty }$
in
$\mathsf {RSpo}_{<\infty }$
in
![]() $\mathsf {ACA}_0$
and a proof of
$\mathsf {ACA}_0$
and a proof of
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
in
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
in
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
. The proofs are not axiomatically optimal, but they can be presented in ordinary mathematical language—meaning without reference to relative computability, technical uses of restricted induction, etc.—and are straightforward to formalize. The
$\Pi ^1_1\text {-}\mathsf {CA}_0$
. The proofs are not axiomatically optimal, but they can be presented in ordinary mathematical language—meaning without reference to relative computability, technical uses of restricted induction, etc.—and are straightforward to formalize. The
![]() $\mathsf {ACA}_0$
proof in particular strikes a good balance between axiomatic simplicity and conceptual simplicity. It is based on Dilworth’s theorem, the fact that chains of order-type
$\mathsf {ACA}_0$
proof in particular strikes a good balance between axiomatic simplicity and conceptual simplicity. It is based on Dilworth’s theorem, the fact that chains of order-type
![]() $\zeta $
are automatically
$\zeta $
are automatically
![]() $(0,\infty )$
-homogeneous, and the observation that a linear order containing no suborder of type
$(0,\infty )$
-homogeneous, and the observation that a linear order containing no suborder of type
![]() $\zeta $
can be partitioned into a well-founded part and a reverse well-founded part. This last observation requires the full strength of
$\zeta $
can be partitioned into a well-founded part and a reverse well-founded part. This last observation requires the full strength of
![]() $\mathsf {ACA}_0$
, as shown by Lemma 4.5. This section also serves to introduce key concepts that will be refined in the next section to prove
$\mathsf {ACA}_0$
, as shown by Lemma 4.5. This section also serves to introduce key concepts that will be refined in the next section to prove
![]() $\mathsf {RSpo}_{<\infty }$
in
$\mathsf {RSpo}_{<\infty }$
in
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
.
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
.
Definition 4.1. Let
![]() $(P, <_P)$
be a partial order, and let
$(P, <_P)$
be a partial order, and let
![]() $X, Y \subseteq P$
.
$X, Y \subseteq P$
.
-
• Write
 $X <_P Y$
if every element of X is strictly below every element of Y:
$X <_P Y$
if every element of X is strictly below every element of Y:
 $\forall x \in X \; \forall y \in Y \; (x <_P y)$
. In the case of singletons, write
$\forall x \in X \; \forall y \in Y \; (x <_P y)$
. In the case of singletons, write
 $x <_P Y$
and
$x <_P Y$
and
 $X <_P y$
in place of
$X <_P y$
in place of
 $\{x\} <_P Y$
and
$\{x\} <_P Y$
and
 $X <_P \{y\}$
.
$X <_P \{y\}$
. -
• Write
 $X \leq _{\forall \exists } Y$
if every element of X is below some element of Y:
$X \leq _{\forall \exists } Y$
if every element of X is below some element of Y:
 $\forall x \in X \; \exists y \in Y \; (x \leq _P y)$
.
$\forall x \in X \; \exists y \in Y \; (x \leq _P y)$
. -
• Write
 $X \mid _P Y$
if every element of X is incomparable with every element of Y:
$X \mid _P Y$
if every element of X is incomparable with every element of Y:
 $\forall x \in X \; \forall y \in Y \; (x \mid _P y)$
. In the case of singletons, write
$\forall x \in X \; \forall y \in Y \; (x \mid _P y)$
. In the case of singletons, write
 $x \mid _P Y$
in place of
$x \mid _P Y$
in place of
 $\{x\} \mid _P Y$
.
$\{x\} \mid _P Y$
.
We also extend the notation of Definition 4.1 to sequences. For example, if
![]() ${A = \langle a_n : n \in \mathbb {N} \rangle }$
and
${A = \langle a_n : n \in \mathbb {N} \rangle }$
and
![]() $B = \langle b_n : n \in \mathbb {N} \rangle $
are sequences in a partial order
$B = \langle b_n : n \in \mathbb {N} \rangle $
are sequences in a partial order
![]() $(P, <_P)$
, then we write
$(P, <_P)$
, then we write
![]() $A \leq _{\forall \exists } B$
if
$A \leq _{\forall \exists } B$
if
![]() $\forall n \, \exists m \, (a_n \leq _P b_m)$
.
$\forall n \, \exists m \, (a_n \leq _P b_m)$
.
Definition 4.2. Let
![]() $(P, <_P)$
be a partial order, and let
$(P, <_P)$
be a partial order, and let
![]() $X \subseteq P$
.
$X \subseteq P$
.
-
• Let
 $X{\downarrow } = \{p \in P : \exists x \in X \; (p \leq _P x)\}$
and
$X{\downarrow } = \{p \in P : \exists x \in X \; (p \leq _P x)\}$
and
 $X{\uparrow } = \{p \in P : \exists x \in X \; (p \geq _P x)\}$
denote the downward and upward closures of X in P, respectively. These sets may be formed in
$X{\uparrow } = \{p \in P : \exists x \in X \; (p \geq _P x)\}$
denote the downward and upward closures of X in P, respectively. These sets may be formed in
 $\mathsf {ACA}_0$
.
$\mathsf {ACA}_0$
. -
• In the case of singletons
 $X = \{x\}$
, write
$X = \{x\}$
, write
 $x{\downarrow }$
and
$x{\downarrow }$
and
 $x{\uparrow }$
in place of
$x{\uparrow }$
in place of
 $\{x\}{\downarrow }$
and
$\{x\}{\downarrow }$
and
 $\{x\}{\uparrow }$
. These sets may be formed in
$\{x\}{\uparrow }$
. These sets may be formed in
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
. -
• Call X well-founded if it contains no infinite descending sequence. Otherwise call X ill-founded. Likewise, call X reverse well-founded if it contains no infinite ascending sequence. Otherwise call X reverse ill-founded.
For a partial order
![]() $(P, <_P)$
and non-empty subsets
$(P, <_P)$
and non-empty subsets
![]() $X, Y, Z \subseteq P$
,
$X, Y, Z \subseteq P$
,
![]() $\mathsf {RCA}_0$
suffices to show that
$\mathsf {RCA}_0$
suffices to show that
![]() $X <_P Y <_P Z$
implies
$X <_P Y <_P Z$
implies
![]() $X <_P Z$
and that
$X <_P Z$
and that
![]() $X \leq _{\forall \exists } Y \leq _{\forall \exists } Z$
implies
$X \leq _{\forall \exists } Y \leq _{\forall \exists } Z$
implies
![]() ${X \leq _{\forall \exists } Z}$
. Also, notice that
${X \leq _{\forall \exists } Z}$
. Also, notice that
![]() $X \leq _{\forall \exists } Y$
simply means that
$X \leq _{\forall \exists } Y$
simply means that
![]() $X \subseteq Y{\downarrow }$
, but beware that forming the set
$X \subseteq Y{\downarrow }$
, but beware that forming the set
![]() $Y{\downarrow }$
requires
$Y{\downarrow }$
requires
![]() $\mathsf {ACA}_0$
in general.
$\mathsf {ACA}_0$
in general.
As mentioned above, we show that partitioning a linear order with no suborder of type
![]() $\zeta $
into a well-founded part and a reverse well-founded part is equivalent to
$\zeta $
into a well-founded part and a reverse well-founded part is equivalent to
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
. More generally, we show that isolating the well-founded part of a partial order that contains no infinite antichain and no suborder of type
$\mathsf {RCA}_0$
. More generally, we show that isolating the well-founded part of a partial order that contains no infinite antichain and no suborder of type
![]() $\zeta $
is equivalent to
$\zeta $
is equivalent to
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
. Finding the well-founded part of such a partial order is used to extend
$\mathsf {RCA}_0$
. Finding the well-founded part of such a partial order is used to extend
![]() $\mathsf {RSpo}_{<\infty }$
to infinite partial orders without infinite antichains in Section 7. The reversal exploits the tool of true and false numbers of an injection
$\mathsf {RSpo}_{<\infty }$
to infinite partial orders without infinite antichains in Section 7. The reversal exploits the tool of true and false numbers of an injection
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
.
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
.
Definition 4.3. Let
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection. An
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection. An
![]() $n \in \mathbb {N}$
is a true number if
$n \in \mathbb {N}$
is a true number if
![]() $\forall k> n \; (f(n) < f(k))$
, and otherwise n is a false number. Additionally, an
$\forall k> n \; (f(n) < f(k))$
, and otherwise n is a false number. Additionally, an
![]() $n \in \mathbb {N}$
is true at stage m if
$n \in \mathbb {N}$
is true at stage m if
![]() $\forall k \, (n < k \leq m \;\rightarrow \; f(n) < f(k))$
, and otherwise n is false at stage m.
$\forall k \, (n < k \leq m \;\rightarrow \; f(n) < f(k))$
, and otherwise n is false at stage m.
The idea of true numbers appears to have originated with Dekker [Reference Dekker10], who called them minimal. True numbers are important because the range of f is recursive in the join of f with any infinite set of true numbers. In fact, if n is a true number, then one can determine
![]() $\operatorname {{\mathrm {ran}}}(f)$
up to
$\operatorname {{\mathrm {ran}}}(f)$
up to
![]() $f(n)$
by simply evaluating f on inputs
$f(n)$
by simply evaluating f on inputs
![]() $0, \dots , n$
. In reverse mathematics, true numbers facilitate reversals to
$0, \dots , n$
. In reverse mathematics, true numbers facilitate reversals to
![]() $\mathsf {ACA}_0$
. To prove that some statement
$\mathsf {ACA}_0$
. To prove that some statement
![]() $\varphi $
implies
$\varphi $
implies
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
, one strategy is to let
$\mathsf {RCA}_0$
, one strategy is to let
![]() $f \colon \mathbb {N} \to \mathbb {N}$
be an injection, use
$f \colon \mathbb {N} \to \mathbb {N}$
be an injection, use
![]() $\varphi $
to produce an infinite set S of true numbers, use f and S to compute
$\varphi $
to produce an infinite set S of true numbers, use f and S to compute
![]() $\operatorname {{\mathrm {ran}}}(f)$
, and then apply Lemma 2.1. For example, this strategy is used in [Reference Frittaion, Hendtlass, Marcone, Shafer and Van der Meeren12, Reference Frittaion and Marcone13, Reference Marcone and Shore25] in the form of the following well-known construction.
$\operatorname {{\mathrm {ran}}}(f)$
, and then apply Lemma 2.1. For example, this strategy is used in [Reference Frittaion, Hendtlass, Marcone, Shafer and Van der Meeren12, Reference Frittaion and Marcone13, Reference Marcone and Shore25] in the form of the following well-known construction.
Construction 4.4. Let
![]() $f\colon \mathbb {N} \to \mathbb {N}$
be an injection. Define a linear order
$f\colon \mathbb {N} \to \mathbb {N}$
be an injection. Define a linear order
![]() $(L, <_L)$
where
$(L, <_L)$
where
![]() $L = \{\ell _n : n \in \mathbb {N}\}$
and for each
$L = \{\ell _n : n \in \mathbb {N}\}$
and for each
![]() $n < m$
the following hold:
$n < m$
the following hold:
-
(1)
 $\ell _n <_L \ell _m$
if
$\ell _n <_L \ell _m$
if
 $f(k) < f(n)$
for some k with
$f(k) < f(n)$
for some k with
 $n <k \leq m$
(i.e., n is false at stage m), and
$n <k \leq m$
(i.e., n is false at stage m), and -
(2)
 $\ell _m <_L \ell _n$
if
$\ell _m <_L \ell _n$
if
 $f(n) < f(k)$
for all k with
$f(n) < f(k)$
for all k with
 $n < k \leq m$
(i.e., n is true at stage m).
$n < k \leq m$
(i.e., n is true at stage m).
This construction can be carried out in
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Given an injection
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
, Construction 4.4 produces a stable linear order either of type
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
, Construction 4.4 produces a stable linear order either of type
![]() $\omega + \omega ^*$
(if f has infinitely many false numbers) or of type
$\omega + \omega ^*$
(if f has infinitely many false numbers) or of type
![]() $k + \omega ^*$
for some finite k (otherwise).
$k + \omega ^*$
for some finite k (otherwise).
![]() $\mathsf {RCA}_0$
proves that n is true if and only if n is in the
$\mathsf {RCA}_0$
proves that n is true if and only if n is in the
![]() $\omega ^*$
-part of L. Therefore,
$\omega ^*$
-part of L. Therefore,
![]() $\mathsf {RCA}_0$
proves that if there is an infinite subset of the
$\mathsf {RCA}_0$
proves that if there is an infinite subset of the
![]() $\omega ^*$
-part of L, or, equivalently, if there is an infinite descending sequence in L, then the range of f exists. For further details, see the proofs of [Reference Marcone and Shore25, Lemma 4.2] and [Reference Frittaion and Marcone13, Theorem 4.5].
$\omega ^*$
-part of L, or, equivalently, if there is an infinite descending sequence in L, then the range of f exists. For further details, see the proofs of [Reference Marcone and Shore25, Lemma 4.2] and [Reference Frittaion and Marcone13, Theorem 4.5].
Lemma 4.5. The following are equivalent over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
-
(1)
 $\mathsf {ACA}_0$
.
$\mathsf {ACA}_0$
. -
(2) For every partial order
 $(P, <_P)$
, if P has no infinite antichain and no suborder of type
$(P, <_P)$
, if P has no infinite antichain and no suborder of type
 $\zeta $
, then there is a set
$\zeta $
, then there is a set
 $W \subseteq P$
such that
$W \subseteq P$
such that
 $\forall p \in P$
(
$\forall p \in P$
(
 $p \in W \;\leftrightarrow \; p{\downarrow }$
is well-founded).
$p \in W \;\leftrightarrow \; p{\downarrow }$
is well-founded). -
(3) Every linear order
 $(L, <_L)$
with no suborder of type
$(L, <_L)$
with no suborder of type
 $\zeta $
can be partitioned as
$\zeta $
can be partitioned as
 $L = W \cup R$
, where
$L = W \cup R$
, where-
•
 $W <_L R$
,
$W <_L R$
, -
• W is well-founded, and
-
• R is reverse well-founded.
-
Proof For (1)
![]() $\Rightarrow $
(2), let
$\Rightarrow $
(2), let
![]() $(P, <_P)$
be a partial order with no infinite antichain and no suborder of type
$(P, <_P)$
be a partial order with no infinite antichain and no suborder of type
![]() $\zeta $
. For the purposes of this proof, call a descending sequence
$\zeta $
. For the purposes of this proof, call a descending sequence
![]() $p_0>_P p_1 >_P \cdots >_P p_n$
in P discrete if for all
$p_0>_P p_1 >_P \cdots >_P p_n$
in P discrete if for all
![]() $i < n$
there is no element of P strictly between
$i < n$
there is no element of P strictly between
![]() $p_i$
and
$p_i$
and
![]() $p_{i+1}$
. Define a sequence of trees
$p_{i+1}$
. Define a sequence of trees
![]() $\langle T_p : p \in P \rangle $
, where for each
$\langle T_p : p \in P \rangle $
, where for each
![]() $p \in P$
,
$p \in P$
,
![]() $T_p$
consists of the finite discrete descending sequences starting at p. That is, for each
$T_p$
consists of the finite discrete descending sequences starting at p. That is, for each
![]() $p \in P$
,
$p \in P$
,
![]() $T_p$
consists of the
$T_p$
consists of the
![]() $\sigma \in P^{<\mathbb {N}}$
such that
$\sigma \in P^{<\mathbb {N}}$
such that
 $$ \begin{align*} (|\sigma| &> 0 \;\rightarrow\; \sigma(0) = p)\\ &\wedge \quad \forall i < |\sigma|-1 \; \Bigl(\sigma(i+1) <_P \sigma(i) \;\wedge\; \neg \exists x \in P \; \bigl(\sigma(i+1) <_P x <_P \sigma(i)\bigr)\Bigr). \end{align*} $$
$$ \begin{align*} (|\sigma| &> 0 \;\rightarrow\; \sigma(0) = p)\\ &\wedge \quad \forall i < |\sigma|-1 \; \Bigl(\sigma(i+1) <_P \sigma(i) \;\wedge\; \neg \exists x \in P \; \bigl(\sigma(i+1) <_P x <_P \sigma(i)\bigr)\Bigr). \end{align*} $$
Let
![]() $W = \{p \in P : T_p \text { is finite}\}$
. We show that
$W = \{p \in P : T_p \text { is finite}\}$
. We show that
![]() $p \in W$
if and only if
$p \in W$
if and only if
![]() $p{\downarrow }$
is well-founded.
$p{\downarrow }$
is well-founded.
First, consider a
![]() $p \in P$
where
$p \in P$
where
![]() $T_p$
is infinite. Given any
$T_p$
is infinite. Given any
![]() $\sigma \in T_p$
, the set
$\sigma \in T_p$
, the set
![]() $\{q \in P : \sigma ^{\smallfrown } q \in T_p\}$
is an antichain on account of the discreteness condition on the elements of
$\{q \in P : \sigma ^{\smallfrown } q \in T_p\}$
is an antichain on account of the discreteness condition on the elements of
![]() $T_p$
and therefore is finite because P has no infinite antichain. Thus T is an infinite finitely branching tree, and therefore T has an infinite path f by König’s lemma. This path provides an infinite descending sequence in P below p, so
$T_p$
and therefore is finite because P has no infinite antichain. Thus T is an infinite finitely branching tree, and therefore T has an infinite path f by König’s lemma. This path provides an infinite descending sequence in P below p, so
![]() $p{\downarrow }$
is ill-founded.
$p{\downarrow }$
is ill-founded.
Conversely, consider a
![]() $p \in P$
where
$p \in P$
where
![]() $T_p$
is finite. Suppose for a contradiction that
$T_p$
is finite. Suppose for a contradiction that
![]() $p{\downarrow }$
is ill-founded, and let
$p{\downarrow }$
is ill-founded, and let
![]() $p = q_0>_P q_1 >_P q_2 >_P \cdots $
be an infinite descending sequence below P. Notice that
$p = q_0>_P q_1 >_P q_2 >_P \cdots $
be an infinite descending sequence below P. Notice that
![]() $\sigma = \langle p \rangle $
is in
$\sigma = \langle p \rangle $
is in
![]() $T_p$
and satisfies
$T_p$
and satisfies
![]() $\sigma (0)>_P q_1$
. Let
$\sigma (0)>_P q_1$
. Let
![]() ${\sigma \in T_p}$
be a non-empty sequence of maximum length for which there is an n such that
${\sigma \in T_p}$
be a non-empty sequence of maximum length for which there is an n such that
![]() ${\sigma (|\sigma |-1)>_P q_n}$
. Such a
${\sigma (|\sigma |-1)>_P q_n}$
. Such a
![]() $\sigma $
exists because
$\sigma $
exists because
![]() $T_p$
is finite. Now define an infinite ascending sequence
$T_p$
is finite. Now define an infinite ascending sequence
![]() $A = \langle a_i : i \in \mathbb {N} \rangle $
with
$A = \langle a_i : i \in \mathbb {N} \rangle $
with
![]() $\sigma (|\sigma |-1)>_P a_i \geq _P q_n$
for all i as follows. Let
$\sigma (|\sigma |-1)>_P a_i \geq _P q_n$
for all i as follows. Let
![]() $a_0 = q_n$
. Given
$a_0 = q_n$
. Given
![]() $a_i$
, let
$a_i$
, let
![]() $a_{i+1}$
be the
$a_{i+1}$
be the
![]() $<$
-least element of P with
$<$
-least element of P with
![]() $\sigma (|\sigma |-1)>_P a_{i+1} >_P a_i$
. Such an
$\sigma (|\sigma |-1)>_P a_{i+1} >_P a_i$
. Such an
![]() $a_{i+1}$
exists because otherwise we would have
$a_{i+1}$
exists because otherwise we would have
![]() $\sigma ^{\smallfrown } a_i \in T_p$
and
$\sigma ^{\smallfrown } a_i \in T_p$
and
![]() $a_i>_P q_{n+1}$
, which contradicts that
$a_i>_P q_{n+1}$
, which contradicts that
![]() $\sigma $
has maximum length. We now have that
$\sigma $
has maximum length. We now have that
![]() $\{a_i : i \in \mathbb {N}\} \cup \{q_i : i> n\}$
is a chain in P of order-type
$\{a_i : i \in \mathbb {N}\} \cup \{q_i : i> n\}$
is a chain in P of order-type
![]() $\zeta $
, which is a contradiction. Thus
$\zeta $
, which is a contradiction. Thus
![]() $p{\downarrow }$
is well-founded, as desired.
$p{\downarrow }$
is well-founded, as desired.
For (2)
![]() $\Rightarrow $
(3), let
$\Rightarrow $
(3), let
![]() $(L, <_L)$
be a linear order with no suborder of type
$(L, <_L)$
be a linear order with no suborder of type
![]() $\zeta $
. Then L has no infinite antichain, so by item (2) there is a set W containing exactly the
$\zeta $
. Then L has no infinite antichain, so by item (2) there is a set W containing exactly the
![]() $p \in P$
for which
$p \in P$
for which
![]() $p{\downarrow }$
is well-founded. Clearly W is downward-closed. Let
$p{\downarrow }$
is well-founded. Clearly W is downward-closed. Let
![]() $R = L \setminus W$
. Then
$R = L \setminus W$
. Then
![]() $L = W \cup R$
and
$L = W \cup R$
and
![]() $W <_L R$
. We show that R is reverse well-founded. First, observe that R has no least element. If r were the least element of R, then
$W <_L R$
. We show that R is reverse well-founded. First, observe that R has no least element. If r were the least element of R, then
![]() $r{\downarrow }$
would be well-founded because every
$r{\downarrow }$
would be well-founded because every
![]() $p <_L r$
would be in W and W is well-founded. This would imply that
$p <_L r$
would be in W and W is well-founded. This would imply that
![]() $r \in W$
, which is a contradiction. Thus either
$r \in W$
, which is a contradiction. Thus either
![]() $R = \emptyset $
, in which case R is reverse well-founded, or R is non-empty and has no minimum element, in which case we can define an infinite descending sequence
$R = \emptyset $
, in which case R is reverse well-founded, or R is non-empty and has no minimum element, in which case we can define an infinite descending sequence
![]() $\langle d_n : n \in \mathbb {N} \rangle $
that is coinitial in R. If R also has an infinite ascending sequence
$\langle d_n : n \in \mathbb {N} \rangle $
that is coinitial in R. If R also has an infinite ascending sequence
![]() $B = \langle b_n : n \in \mathbb {N} \rangle $
, then
$B = \langle b_n : n \in \mathbb {N} \rangle $
, then
![]() $b_0>_L d_{n_0}$
for some
$b_0>_L d_{n_0}$
for some
![]() $n_0$
, in which case
$n_0$
, in which case
![]() $\{d_n : n> n_0\} \cup B$
is a contradictory suborder of L of type
$\{d_n : n> n_0\} \cup B$
is a contradictory suborder of L of type
![]() $\zeta $
. Thus R is reverse well-founded.
$\zeta $
. Thus R is reverse well-founded.
For (3)
![]() $\Rightarrow $
(1), let
$\Rightarrow $
(1), let
![]() $f \colon \mathbb {N} \to \mathbb {N}$
be an injection. We show that the true numbers for f form a set. This implies that the range of f exists as a set, which implies
$f \colon \mathbb {N} \to \mathbb {N}$
be an injection. We show that the true numbers for f form a set. This implies that the range of f exists as a set, which implies
![]() $\mathsf {ACA}_0$
by Lemma 2.1.
$\mathsf {ACA}_0$
by Lemma 2.1.
If f has only finitely many false numbers, then the set of all false numbers exists by bounded
![]() $\Sigma ^0_1$
comprehension, in which case the set of true numbers also exists.
$\Sigma ^0_1$
comprehension, in which case the set of true numbers also exists.
Suppose instead that f has infinitely many false numbers. Let
![]() $(L, <_L)$
be the linear order defined as in Construction 4.4 for f. Recall that in this case
$(L, <_L)$
be the linear order defined as in Construction 4.4 for f. Recall that in this case
![]() $L = \{\ell _n : n \in \mathbb {N}\}$
is a linear order of type
$L = \{\ell _n : n \in \mathbb {N}\}$
is a linear order of type
![]() $\omega + \omega ^*$
, where, for each n,
$\omega + \omega ^*$
, where, for each n,
![]() $\ell _n$
is in the
$\ell _n$
is in the
![]() $\omega $
-part if n is false and
$\omega $
-part if n is false and
![]() $\ell _n$
is in the
$\ell _n$
is in the
![]() $\omega ^*$
-part if n is true. We define a new linear order
$\omega ^*$
-part if n is true. We define a new linear order
![]() $(S, <_S)$
from L by replacing each element in the
$(S, <_S)$
from L by replacing each element in the
![]() $\omega ^*$
-part of L by an infinite descending sequence and by replacing each element in the
$\omega ^*$
-part of L by an infinite descending sequence and by replacing each element in the
![]() $\omega $
-part of L by a finite descending sequence. This way,
$\omega $
-part of L by a finite descending sequence. This way,
![]() $\mathsf {RCA}_0$
suffices to verify that elements in the
$\mathsf {RCA}_0$
suffices to verify that elements in the
![]() $\omega ^*$
-part of L give rise to elements in the ill-founded part of S and that elements in the
$\omega ^*$
-part of L give rise to elements in the ill-founded part of S and that elements in the
![]() $\omega $
-part of L give rise to elements in the well-founded part of S. To do this, let
$\omega $
-part of L give rise to elements in the well-founded part of S. To do this, let
![]() $S = \{s_{n,m} : n, m \in \mathbb {N} \text { and } n \text { is true at stage } m\}$
(note that if
$S = \{s_{n,m} : n, m \in \mathbb {N} \text { and } n \text { is true at stage } m\}$
(note that if
![]() $m \leq n$
, then n is true at stage m), and define
$m \leq n$
, then n is true at stage m), and define
Observe that if
![]() $n_0$
is false and
$n_0$
is false and
![]() $n_1$
is true, then
$n_1$
is true, then
![]() $\ell _{n_0} <_L \ell _{n_1}$
, so
$\ell _{n_0} <_L \ell _{n_1}$
, so
![]() $s_{n_0, m_0} <_S s_{n_1, m_1}$
for every
$s_{n_0, m_0} <_S s_{n_1, m_1}$
for every
![]() $m_0$
and
$m_0$
and
![]() $m_1$
. Thus no infinite ascending sequence in S can contain an element
$m_1$
. Thus no infinite ascending sequence in S can contain an element
![]() $s_{n,m}$
where n is true, and no infinite descending sequence in S can contain an element
$s_{n,m}$
where n is true, and no infinite descending sequence in S can contain an element
![]() $s_{n,m}$
where n is false. It follows that S cannot contain a suborder of type
$s_{n,m}$
where n is false. It follows that S cannot contain a suborder of type
![]() $\zeta $
because such a suborder would have to contain some element
$\zeta $
because such a suborder would have to contain some element
![]() $s_{n,m}$
, and
$s_{n,m}$
, and
![]() $s_{n,m}$
is either in no infinite ascending sequence or in no infinite descending sequence. We may therefore apply item (3) to S and obtain a partition
$s_{n,m}$
is either in no infinite ascending sequence or in no infinite descending sequence. We may therefore apply item (3) to S and obtain a partition
![]() $S = W \cup R$
where
$S = W \cup R$
where
![]() $W <_L R$
, W is well-founded, and R is reverse well-founded. We claim that
$W <_L R$
, W is well-founded, and R is reverse well-founded. We claim that
![]() $s_{n, 0} \in R$
if and only if n is true. If n is true, then
$s_{n, 0} \in R$
if and only if n is true. If n is true, then
![]() $s_{n,m} \in S$
for every m, and
$s_{n,m} \in S$
for every m, and
![]() $s_{n,0}>_S s_{n,1} >_S \cdots $
is an infinite descending sequence in S. Thus
$s_{n,0}>_S s_{n,1} >_S \cdots $
is an infinite descending sequence in S. Thus
![]() $s_{n,0}$
cannot be in W as then W would be ill-founded. So
$s_{n,0}$
cannot be in W as then W would be ill-founded. So
![]() $s_{n,0} \in R$
. Conversely, if n is false, then, using the assumption that there are infinitely many false numbers, we can define an infinite ascending sequence
$s_{n,0} \in R$
. Conversely, if n is false, then, using the assumption that there are infinitely many false numbers, we can define an infinite ascending sequence
![]() $\ell _n = \ell _{k_0} <_L \ell _{k_1} <_L \cdots $
in L as follows. Set
$\ell _n = \ell _{k_0} <_L \ell _{k_1} <_L \cdots $
in L as follows. Set
![]() $k_0 = n$
. Given
$k_0 = n$
. Given
![]() $k_i$
, search for the first pair
$k_i$
, search for the first pair
![]() $\langle k, m \rangle $
where
$\langle k, m \rangle $
where
![]() $\ell _{k_i} <_L \ell _k$
and k is false at stage m, and set
$\ell _{k_i} <_L \ell _k$
and k is false at stage m, and set
![]() $k_{i+1} = k$
. We then have the corresponding infinite ascending sequence
$k_{i+1} = k$
. We then have the corresponding infinite ascending sequence
![]() $s_{n,0} = s_{k_0, 0} <_S s_{k_1, 0} <_S \cdots $
in S. Thus
$s_{n,0} = s_{k_0, 0} <_S s_{k_1, 0} <_S \cdots $
in S. Thus
![]() $s_{n,0}$
cannot be in R as then R would not be reverse well-founded. Therefore
$s_{n,0}$
cannot be in R as then R would not be reverse well-founded. Therefore
![]() $\{n : s_{n,0} \in R\}$
is the set of true numbers for f, which completes the proof.
$\{n : s_{n,0} \in R\}$
is the set of true numbers for f, which completes the proof.
By taking complements and/or reversing the partial order, the statement “
![]() $p{\downarrow }$
is well-founded” may be replaced by any of “
$p{\downarrow }$
is well-founded” may be replaced by any of “
![]() $p{\downarrow }$
is ill-founded,” “
$p{\downarrow }$
is ill-founded,” “
![]() $p{\uparrow }$
is reverse well-founded,” and “
$p{\uparrow }$
is reverse well-founded,” and “
![]() $p{\uparrow }$
is reverse ill-founded” in Lemma 4.5 item (2) and the lemma remains true.
$p{\uparrow }$
is reverse ill-founded” in Lemma 4.5 item (2) and the lemma remains true.
The proof that
![]() $\mathsf {ACA}_0$
implies Lemma 4.5 item (2) is uniform with respect to the partial order. That is,
$\mathsf {ACA}_0$
implies Lemma 4.5 item (2) is uniform with respect to the partial order. That is,
![]() $\mathsf {ACA}_0$
proves that if
$\mathsf {ACA}_0$
proves that if
![]() $P_0, P_1, P_2, \dots $
is a sequence of partial orders without infinite antichains or suborders of type
$P_0, P_1, P_2, \dots $
is a sequence of partial orders without infinite antichains or suborders of type
![]() $\zeta $
, then there is a sequence of sets
$\zeta $
, then there is a sequence of sets
![]() $W_0, W_1, W_2, \dots $
where, for each i,
$W_0, W_1, W_2, \dots $
where, for each i,
![]() $W_i$
consists of exactly the
$W_i$
consists of exactly the
![]() $p \in P_i$
such that
$p \in P_i$
such that
![]() $p{\downarrow }$
is well-founded. The proof that
$p{\downarrow }$
is well-founded. The proof that
![]() $\mathsf {ACA}_0$
implies Lemma 4.5 item (3) is similarly uniform. In fact, to conclude Lemma 4.5 item (3) for a finite sequence of linear orders
$\mathsf {ACA}_0$
implies Lemma 4.5 item (3) is similarly uniform. In fact, to conclude Lemma 4.5 item (3) for a finite sequence of linear orders
![]() $L_0, L_1, \dots , L_{n-1}$
, as we shall need in Theorem 4.9, one application of Lemma 4.5 item (2) suffices. Given linear orders
$L_0, L_1, \dots , L_{n-1}$
, as we shall need in Theorem 4.9, one application of Lemma 4.5 item (2) suffices. Given linear orders
![]() $L_0, L_1, \dots , L_{n-1}$
without suborders of type
$L_0, L_1, \dots , L_{n-1}$
without suborders of type
![]() $\zeta $
, let P be the partial order consisting of the disjoint union of the linear orders
$\zeta $
, let P be the partial order consisting of the disjoint union of the linear orders
![]() $L_i$
for
$L_i$
for
![]() $i < n$
. Then P has no infinite antichain and no suborder of type
$i < n$
. Then P has no infinite antichain and no suborder of type
![]() $\zeta $
, so by Lemma 4.5 item (2), there is a set W consisting of exactly the
$\zeta $
, so by Lemma 4.5 item (2), there is a set W consisting of exactly the
![]() $p \in P$
such that
$p \in P$
such that
![]() $p{\downarrow }$
is well-founded. Then let
$p{\downarrow }$
is well-founded. Then let
![]() $W_i = L_i \cap W$
and
$W_i = L_i \cap W$
and
![]() $R_i = L_i \setminus W$
for each
$R_i = L_i \setminus W$
for each
![]() $i < n$
.
$i < n$
.
If an infinite ascending sequence
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
in a partial order
$A = \langle a_n : n \in \mathbb {N} \rangle $
in a partial order
![]() $(P, <_P)$
is not
$(P, <_P)$
is not
![]() $(0,\infty )$
-homogeneous, then there is a
$(0,\infty )$
-homogeneous, then there is a
![]() $p \in P$
that is comparable with some elements of P, but only finitely many. As A is an ascending sequence, this means that there is an
$p \in P$
that is comparable with some elements of P, but only finitely many. As A is an ascending sequence, this means that there is an
![]() $n_0$
such that
$n_0$
such that
![]() $p>_P a_{n_0}$
, but
$p>_P a_{n_0}$
, but
![]() $\forall n> n_0 \, (p \mid _P a_n)$
. We think of such a p as a counterexample to A being
$\forall n> n_0 \, (p \mid _P a_n)$
. We think of such a p as a counterexample to A being
![]() $(0,\infty )$
-homogeneous. Indeed, p is also a counterexample to
$(0,\infty )$
-homogeneous. Indeed, p is also a counterexample to
![]() $\langle a_n : n \geq n_0 \rangle $
being
$\langle a_n : n \geq n_0 \rangle $
being
![]() $(0,\infty )$
-homogeneous.
$(0,\infty )$
-homogeneous.
Definition 4.6. Let
![]() $(P, <_P)$
be a partial order, and let
$(P, <_P)$
be a partial order, and let
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
be an ascending sequence in P. Then
$A = \langle a_n : n \in \mathbb {N} \rangle $
be an ascending sequence in P. Then
![]() $A_{\geq n_0}$
denotes the ascending sequence
$A_{\geq n_0}$
denotes the ascending sequence
![]() $\langle a_n : n \geq n_0 \rangle $
. Sequences of the form
$\langle a_n : n \geq n_0 \rangle $
. Sequences of the form
![]() $A_{\geq n_0}$
are called tails of A, which can be formed in
$A_{\geq n_0}$
are called tails of A, which can be formed in
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Definition 4.7. Let
![]() $(P, <_P)$
be a partial order, and let
$(P, <_P)$
be a partial order, and let
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in P. A
$A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in P. A
![]() $p \in P$
is called a counterexample to A if there is an n such that
$p \in P$
is called a counterexample to A if there is an n such that
![]() $p>_P a_n$
and
$p>_P a_n$
and
![]() $p \mid _P A_{\geq n+1}$
. An infinite ascending sequence
$p \mid _P A_{\geq n+1}$
. An infinite ascending sequence
![]() $B = \langle b_{\ell } : \ell \in \mathbb {N} \rangle $
is called a counterexample sequence for A if B contains counterexamples to infinitely many tails of A:
$B = \langle b_{\ell } : \ell \in \mathbb {N} \rangle $
is called a counterexample sequence for A if B contains counterexamples to infinitely many tails of A:
![]() $\forall m \; \exists n> m \; \exists \ell \; (b_{\ell } >_P a_n \;\wedge \; b_{\ell } \mid _P A_{\geq n+1})$
.
$\forall m \; \exists n> m \; \exists \ell \; (b_{\ell } >_P a_n \;\wedge \; b_{\ell } \mid _P A_{\geq n+1})$
.
Notice that if B is a counterexample sequence for an infinite ascending sequence A in some partial order
![]() $(P, <_P)$
, then
$(P, <_P)$
, then
![]() $A \leq _{\forall \exists } B$
, but
$A \leq _{\forall \exists } B$
, but
![]() $B \nleq _{\forall \exists } A$
.
$B \nleq _{\forall \exists } A$
.
Suppose that A is an infinite ascending sequence in a partial order
![]() $(P, <_P)$
where no tail of A is
$(P, <_P)$
where no tail of A is
![]() $(0,\infty )$
-homogeneous. Then for every n, there is a counterexample p to
$(0,\infty )$
-homogeneous. Then for every n, there is a counterexample p to
![]() $A_{\geq n}$
. If P has finite width, then we can make a counterexample sequence out of such counterexamples.
$A_{\geq n}$
. If P has finite width, then we can make a counterexample sequence out of such counterexamples.
Lemma 4.8. The following is provable in
![]() $\mathsf {ACA}_0$
. Let
$\mathsf {ACA}_0$
. Let
![]() $(P,<_P)$
be an infinite partial order with k-chain decomposition
$(P,<_P)$
be an infinite partial order with k-chain decomposition
![]() $C_0, \dots , C_{k-1}$
. Let
$C_0, \dots , C_{k-1}$
. Let
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in
$A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in
![]() $C_i$
for some
$C_i$
for some
![]() $i < k$
, and assume that no tail of A is
$i < k$
, and assume that no tail of A is
![]() $(0,\infty )$
-homogeneous. Then there is an infinite ascending sequence
$(0,\infty )$
-homogeneous. Then there is an infinite ascending sequence
![]() $B = \langle b_n : n \in \mathbb {N} \rangle $
in
$B = \langle b_n : n \in \mathbb {N} \rangle $
in
![]() $C_j$
for some
$C_j$
for some
![]() $j < k$
that is a counterexample sequence for A.
$j < k$
that is a counterexample sequence for A.
Proof We assume that no tail of A is
![]() $(0,\infty )$
-homogeneous, so every tail of A has a counterexample p. For each n, let
$(0,\infty )$
-homogeneous, so every tail of A has a counterexample p. For each n, let
![]() $p_n$
be the
$p_n$
be the
![]() $<$
-least counterexample to the tail
$<$
-least counterexample to the tail
![]() $A_{\geq n}$
. By
$A_{\geq n}$
. By
![]() $\mathsf {RT}^1_{<\infty }$
, there are a
$\mathsf {RT}^1_{<\infty }$
, there are a
![]() $j < k$
and an infinite
$j < k$
and an infinite
![]() $X \subseteq \mathbb {N}$
such that
$X \subseteq \mathbb {N}$
such that
![]() $p_n \in C_j$
for all
$p_n \in C_j$
for all
![]() $n \in X$
. Now, for every
$n \in X$
. Now, for every
![]() $n \in X$
, we have that
$n \in X$
, we have that
![]() $p_n <_P p_m$
for all sufficiently large
$p_n <_P p_m$
for all sufficiently large
![]() $m \in X$
. To see this, let
$m \in X$
. To see this, let
![]() $n \in X$
. As
$n \in X$
. As
![]() $p_n$
is a counterexample to
$p_n$
is a counterexample to
![]() $A_{\geq n}$
, there is an
$A_{\geq n}$
, there is an
![]() $s \geq n$
such that
$s \geq n$
such that
![]() $p_n>_P a_s$
and
$p_n>_P a_s$
and
![]() $p_n \mid _P A_{\geq s+1}$
. Let
$p_n \mid _P A_{\geq s+1}$
. Let
![]() $m \in X$
be such that
$m \in X$
be such that
![]() $m> s+1$
, and consider
$m> s+1$
, and consider
![]() $p_m$
. The chain
$p_m$
. The chain
![]() $C_j$
contains both
$C_j$
contains both
![]() $p_n$
and
$p_n$
and
![]() $p_m$
, so
$p_m$
, so
![]() $p_n \lessgtr _P p_m$
. As
$p_n \lessgtr _P p_m$
. As
![]() $p_m$
is a counterexample to
$p_m$
is a counterexample to
![]() $A_{\geq m}$
, there is a
$A_{\geq m}$
, there is a
![]() $t \geq m$
such that
$t \geq m$
such that
![]() $p_m>_P a_t$
. Thus we cannot have
$p_m>_P a_t$
. Thus we cannot have
![]() $p_m \leq _P p_n$
because this would yield
$p_m \leq _P p_n$
because this would yield
![]() $a_{s+1} <_P a_t <_P p_m \leq _P p_n$
, contradicting that
$a_{s+1} <_P a_t <_P p_m \leq _P p_n$
, contradicting that
![]() $p_n \mid _P a_{s+1}$
. Note here that
$p_n \mid _P a_{s+1}$
. Note here that
![]() $s+1 < m \leq t$
, so
$s+1 < m \leq t$
, so
![]() $a_{s+1} <_P a_t$
because A is an ascending sequence. Thus it must be that
$a_{s+1} <_P a_t$
because A is an ascending sequence. Thus it must be that
![]() $p_n <_P p_m$
. We may then define the desired counterexample sequence B as follows. Let
$p_n <_P p_m$
. We may then define the desired counterexample sequence B as follows. Let
![]() $n_0$
be the
$n_0$
be the
![]() $<$
-least element of X. Given
$<$
-least element of X. Given
![]() $n_{\ell }$
, let
$n_{\ell }$
, let
![]() $n_{\ell +1}$
be the
$n_{\ell +1}$
be the
![]() $<$
-least element of X with
$<$
-least element of X with
![]() $n_{\ell } < n_{\ell +1}$
and
$n_{\ell } < n_{\ell +1}$
and
![]() $p_{n_{\ell }} <_P p_{n_{\ell +1}}$
. Finally, take
$p_{n_{\ell }} <_P p_{n_{\ell +1}}$
. Finally, take
![]() $b_{\ell } = p_{n_{\ell }}$
for each
$b_{\ell } = p_{n_{\ell }}$
for each
![]() $\ell $
.
$\ell $
.
We are now prepared to give a proof of
![]() $\mathsf {RSpo}_{<\infty }$
in
$\mathsf {RSpo}_{<\infty }$
in
![]() $\mathsf {ACA}_0$
.
$\mathsf {ACA}_0$
.
Theorem 4.9.
![]() $\mathsf {ACA}_0 \vdash \mathsf {RSpo}_{<\infty }$
.
$\mathsf {ACA}_0 \vdash \mathsf {RSpo}_{<\infty }$
.
Proof It suffices to show that
![]() $\mathsf {ACA}_0 \vdash \mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
because
$\mathsf {ACA}_0 \vdash \mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
because
![]() $\mathsf {RSpo}_{<\infty }$
and
$\mathsf {RSpo}_{<\infty }$
and
![]() $\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
are equivalent over
$\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
are equivalent over
![]() $\mathsf {RCA}_0$
as explained in Section 3. In fact, here we may use that
$\mathsf {RCA}_0$
as explained in Section 3. In fact, here we may use that
![]() $\mathsf {WKL}_0 \vdash \forall k \, (\mathsf {RSpo}_k \leftrightarrow \mathsf {RSpo}^{\mathsf {CD}}_k)$
, which is simpler than appealing to Theorem 3.5.
$\mathsf {WKL}_0 \vdash \forall k \, (\mathsf {RSpo}_k \leftrightarrow \mathsf {RSpo}^{\mathsf {CD}}_k)$
, which is simpler than appealing to Theorem 3.5.
Let
![]() $(P, <_P)$
be an infinite partial order with k-chain decomposition
$(P, <_P)$
be an infinite partial order with k-chain decomposition
![]() $C_0, \dots , C_{k-1}$
for some k. Assume for a contradiction that P does not contain a
$C_0, \dots , C_{k-1}$
for some k. Assume for a contradiction that P does not contain a
![]() $(0,\infty )$
-homogeneous chain. Then P contains no chain of order-type
$(0,\infty )$
-homogeneous chain. Then P contains no chain of order-type
![]() $\zeta $
because such a chain is automatically
$\zeta $
because such a chain is automatically
![]() $(0,\infty )$
-homogeneous. In particular, no
$(0,\infty )$
-homogeneous. In particular, no
![]() $C_i$
for
$C_i$
for
![]() $i < k$
contains a chain of order-type
$i < k$
contains a chain of order-type
![]() $\zeta $
, so each
$\zeta $
, so each
![]() $C_i$
may be viewed as a linear order with no suborder of type
$C_i$
may be viewed as a linear order with no suborder of type
![]() $\zeta $
. As discussed above, the (1)
$\zeta $
. As discussed above, the (1)
![]() $\Rightarrow $
(3) direction of Lemma 4.5 generalizes to simultaneously handle any sequence of linear orders without suborders of type
$\Rightarrow $
(3) direction of Lemma 4.5 generalizes to simultaneously handle any sequence of linear orders without suborders of type
![]() $\zeta $
. Apply this to the chains
$\zeta $
. Apply this to the chains
![]() $C_0, \dots , C_{k-1}$
to partition
$C_0, \dots , C_{k-1}$
to partition
![]() $C_i$
for each
$C_i$
for each
![]() $i < k$
into
$i < k$
into
![]() $C_i = W_i \cup R_i$
, where
$C_i = W_i \cup R_i$
, where
![]() $W_i <_P R_i$
,
$W_i <_P R_i$
,
![]() $W_i$
is well-founded, and
$W_i$
is well-founded, and
![]() $R_i$
is reverse well-founded.
$R_i$
is reverse well-founded.
By
![]() $\mathsf {RT}^1_{<\infty }$
, either
$\mathsf {RT}^1_{<\infty }$
, either
![]() $W_i$
is infinite for some
$W_i$
is infinite for some
![]() $i < k$
or
$i < k$
or
![]() $R_i$
is infinite for some
$R_i$
is infinite for some
![]() $i < k$
. Without loss of generality, we may assume that some
$i < k$
. Without loss of generality, we may assume that some
![]() $W_i$
is infinite because otherwise we could work with the reversed partial order
$W_i$
is infinite because otherwise we could work with the reversed partial order
![]() $(P,>_P)$
instead. Relabel the chains
$(P,>_P)$
instead. Relabel the chains
![]() $C_0, \dots , C_{k-1}$
so that the infinite chains
$C_0, \dots , C_{k-1}$
so that the infinite chains
![]() $W_i$
are exactly
$W_i$
are exactly
![]() $W_0, \dots , W_{u-1}$
for some u with
$W_0, \dots , W_{u-1}$
for some u with
![]() $0 < u \leq k$
. For each
$0 < u \leq k$
. For each
![]() $i < u$
, let
$i < u$
, let
![]() $\widehat {W}_i = \{p \in W_i : \forall n \; \exists q> n \; (q >_P p \;\wedge \; q \in W_i)\}$
be the elements of
$\widehat {W}_i = \{p \in W_i : \forall n \; \exists q> n \; (q >_P p \;\wedge \; q \in W_i)\}$
be the elements of
![]() $W_i$
with infinitely many successors in
$W_i$
with infinitely many successors in
![]() $W_i$
. The set
$W_i$
. The set
![]() $W_i \setminus \widehat {W}_i$
is finite for each
$W_i \setminus \widehat {W}_i$
is finite for each
![]() $i < u$
because if
$i < u$
because if
![]() $W_i \setminus \widehat {W}_i$
were infinite, then it would be a chain in
$W_i \setminus \widehat {W}_i$
were infinite, then it would be a chain in
![]() $W_i$
of order-type
$W_i$
of order-type
![]() $\omega ^*$
, which contradicts that
$\omega ^*$
, which contradicts that
![]() $W_i$
is well-founded. It follows that
$W_i$
is well-founded. It follows that
![]() $\widehat {W}_i$
is infinite, well-founded, and has no maximum element for each
$\widehat {W}_i$
is infinite, well-founded, and has no maximum element for each
![]() $i < u$
. Therefore, for each
$i < u$
. Therefore, for each
![]() $i < u$
we can define an infinite ascending sequence
$i < u$
we can define an infinite ascending sequence
![]() $A_i$
in
$A_i$
in
![]() $\widehat {W}_i$
that is cofinal in
$\widehat {W}_i$
that is cofinal in
![]() $\widehat {W}_i$
.
$\widehat {W}_i$
.
We assume that P does not contain a
![]() $(0,\infty )$
-homogeneous chain, so no tail of
$(0,\infty )$
-homogeneous chain, so no tail of
![]() $A_i$
is
$A_i$
is
![]() $(0,\infty )$
-homogeneous for any
$(0,\infty )$
-homogeneous for any
![]() $i < u$
. The argument of Lemma 4.8 generalizes to simultaneously handle any sequence of infinite ascending sequences. Apply this to the sequences
$i < u$
. The argument of Lemma 4.8 generalizes to simultaneously handle any sequence of infinite ascending sequences. Apply this to the sequences
![]() $A_0, \dots , A_{u-1}$
to obtain infinite ascending sequences
$A_0, \dots , A_{u-1}$
to obtain infinite ascending sequences
![]() $B_0, \dots , B_{u-1}$
and a function
$B_0, \dots , B_{u-1}$
and a function
![]() $h \colon u \rightarrow k$
such that for each
$h \colon u \rightarrow k$
such that for each
![]() $i < u$
,
$i < u$
,
![]() $B_i$
is a counterexample sequence to
$B_i$
is a counterexample sequence to
![]() $A_i$
that is contained in chain
$A_i$
that is contained in chain
![]() $C_{h(i)}$
. Notice that
$C_{h(i)}$
. Notice that
![]() $B_i \cap R_{h(i)} = \emptyset $
for each
$B_i \cap R_{h(i)} = \emptyset $
for each
![]() $i < u$
because
$i < u$
because
![]() $B_i$
is an ascending sequence and
$B_i$
is an ascending sequence and
![]() $R_{h(i)}$
is reverse well-founded. Thus
$R_{h(i)}$
is reverse well-founded. Thus
![]() $B_i \subseteq W_{h(i)}$
, which means that
$B_i \subseteq W_{h(i)}$
, which means that
![]() $W_{h(i)}$
is infinite and therefore that
$W_{h(i)}$
is infinite and therefore that
![]() $h(i) < u$
. Thus h is in fact a function
$h(i) < u$
. Thus h is in fact a function
![]() $h \colon u \rightarrow u$
. Furthermore,
$h \colon u \rightarrow u$
. Furthermore,
![]() $B_i \subseteq \widehat {W}_{h(i)}$
because every element of
$B_i \subseteq \widehat {W}_{h(i)}$
because every element of
![]() $B_i$
has infinitely many successors in
$B_i$
has infinitely many successors in
![]() $W_{h(i)}$
.
$W_{h(i)}$
.
Now observe that
![]() $B_i \leq _{\forall \exists } A_{h(i)}$
for each
$B_i \leq _{\forall \exists } A_{h(i)}$
for each
![]() $i < u$
because
$i < u$
because
![]() $B_i \subseteq \widehat {W}_{h(i)}$
and
$B_i \subseteq \widehat {W}_{h(i)}$
and
![]() $A_{h(i)}$
is cofinal in
$A_{h(i)}$
is cofinal in
![]() $\widehat {W}_{h(i)}$
. Additionally,
$\widehat {W}_{h(i)}$
. Additionally,
![]() $A_{h(i)} \leq _{\forall \exists } B_{h(i)}$
for each
$A_{h(i)} \leq _{\forall \exists } B_{h(i)}$
for each
![]() $i < u$
because
$i < u$
because
![]() $B_{h(i)}$
is a counterexample sequence for
$B_{h(i)}$
is a counterexample sequence for
![]() $A_{h(i)}$
. Therefore
$A_{h(i)}$
. Therefore
![]() $B_i \leq _{\forall \exists } A_{h(i)} \leq _{\forall \exists } B_{h(i)}$
, so
$B_i \leq _{\forall \exists } A_{h(i)} \leq _{\forall \exists } B_{h(i)}$
, so
![]() $B_i \leq _{\forall \exists } B_{h(i)}$
for each
$B_i \leq _{\forall \exists } B_{h(i)}$
for each
![]() $i < u$
by transitivity. Let
$i < u$
by transitivity. Let
![]() $h^n$
denote the n
th iterate of h, where
$h^n$
denote the n
th iterate of h, where
![]() $h^0(i) = i$
and
$h^0(i) = i$
and
![]() $h^{n+1}(i) = h(h^n(i))$
for each
$h^{n+1}(i) = h(h^n(i))$
for each
![]() $i < u$
. By induction, we obtain that
$i < u$
. By induction, we obtain that
![]() $B_{h^m(i)} \leq _{\forall \exists } B_{h^n(i)}$
for all
$B_{h^m(i)} \leq _{\forall \exists } B_{h^n(i)}$
for all
![]() $i < u$
whenever
$i < u$
whenever
![]() $m \leq n$
. By the pigeonhole principle, there are
$m \leq n$
. By the pigeonhole principle, there are
![]() $m < n \leq u$
with
$m < n \leq u$
with
![]() $h^m(0) = h^n(0)$
. We then have that
$h^m(0) = h^n(0)$
. We then have that
and therefore that
![]() $B_{h^{m+1}(0)} \leq _{\forall \exists } A_{h^{m+1}(0)}$
by transitivity. This contradicts that
$B_{h^{m+1}(0)} \leq _{\forall \exists } A_{h^{m+1}(0)}$
by transitivity. This contradicts that
![]() $B_{h^{m+1}(0)}$
is a counterexample sequence for
$B_{h^{m+1}(0)}$
is a counterexample sequence for
![]() $A_{h^{m+1}(0)}$
, which completes the proof.
$A_{h^{m+1}(0)}$
, which completes the proof.
If we want a
![]() $(0,\mathrm {cof})$
-homogeneous chain rather than a
$(0,\mathrm {cof})$
-homogeneous chain rather than a
![]() $(0,\infty )$
-homogeneous chain in a given partial order
$(0,\infty )$
-homogeneous chain in a given partial order
![]() $(P, <_P)$
of finite width, then we may no longer assume that P contains no suborder of type
$(P, <_P)$
of finite width, then we may no longer assume that P contains no suborder of type
![]() $\zeta $
, and we may no longer apply Lemma 4.5 item (3) to partition each chain
$\zeta $
, and we may no longer apply Lemma 4.5 item (3) to partition each chain
![]() $C_i$
into well-founded and reverse well-founded parts. Instead, we may directly define the reverse ill-founded part of each
$C_i$
into well-founded and reverse well-founded parts. Instead, we may directly define the reverse ill-founded part of each
![]() $C_i$
and then proceed as before. This pushes the complexity up to
$C_i$
and then proceed as before. This pushes the complexity up to
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
because defining the set of reverse ill-founded elements in a linear order requires
$\Pi ^1_1\text {-}\mathsf {CA}_0$
because defining the set of reverse ill-founded elements in a linear order requires
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
in general, as shown in Theorem 8.3.
$\Pi ^1_1\text {-}\mathsf {CA}_0$
in general, as shown in Theorem 8.3.
Theorem 4.10.
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0 \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
.
$\Pi ^1_1\text {-}\mathsf {CA}_0 \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
.
Proof It suffices to show that
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0 \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
because
$\Pi ^1_1\text {-}\mathsf {CA}_0 \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
because
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
and
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
and
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
are equivalent as explained in Section 3.
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
are equivalent as explained in Section 3.
Let
![]() $(P, <_P)$
be an infinite partial order with k-chain decomposition
$(P, <_P)$
be an infinite partial order with k-chain decomposition
![]() $C_0, \dots , C_{k-1}$
for some k. Apply
$C_0, \dots , C_{k-1}$
for some k. Apply
![]() $\mathsf {RT}^1_{<\infty }$
to conclude that
$\mathsf {RT}^1_{<\infty }$
to conclude that
![]() $C_i$
is infinite for some
$C_i$
is infinite for some
![]() $i < k$
, and apply
$i < k$
, and apply
![]() $\mathsf {ADS}$
to
$\mathsf {ADS}$
to
![]() $C_i$
to conclude that
$C_i$
to conclude that
![]() $C_i$
contains either an infinite ascending sequence or an infinite descending sequence. By reversing the partial order if necessary, we may assume that
$C_i$
contains either an infinite ascending sequence or an infinite descending sequence. By reversing the partial order if necessary, we may assume that
![]() $C_i$
contains an infinite ascending sequence. We show that P contains a
$C_i$
contains an infinite ascending sequence. We show that P contains a
![]() $(0,\infty )$
-homogeneous chain of order-type
$(0,\infty )$
-homogeneous chain of order-type
![]() $\omega $
, which is necessarily
$\omega $
, which is necessarily
![]() $(0,\mathrm {cof})$
-homogeneous as discussed following Definition 3.2. Thus assume for a contradiction that P does not contain a
$(0,\mathrm {cof})$
-homogeneous as discussed following Definition 3.2. Thus assume for a contradiction that P does not contain a
![]() $(0,\infty )$
-homogeneous chain of order-type
$(0,\infty )$
-homogeneous chain of order-type
![]() $\omega $
.
$\omega $
.
Use
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
(and the fact that the
$\Pi ^1_1\text {-}\mathsf {CA}_0$
(and the fact that the
![]() $\Sigma ^1_1$
sets are the complements of the
$\Sigma ^1_1$
sets are the complements of the
![]() $\Pi ^1_1$
sets) to simultaneously define for each
$\Pi ^1_1$
sets) to simultaneously define for each
![]() $i < k$
the subset
$i < k$
the subset
![]() $W_i = \{p \in C_i : p{\uparrow } \cap C_i \text { is reverse ill-founded}\}$
of
$W_i = \{p \in C_i : p{\uparrow } \cap C_i \text { is reverse ill-founded}\}$
of
![]() $C_i$
consisting of the elements of
$C_i$
consisting of the elements of
![]() $C_i$
that have infinite ascending sequences above them in
$C_i$
that have infinite ascending sequences above them in
![]() $C_i$
. At least one
$C_i$
. At least one
![]() $W_i$
is non-empty because at least one
$W_i$
is non-empty because at least one
![]() $C_i$
contains an infinite ascending sequence. Now proceed as in the proof of Theorem 4.9, except notice that now the sets
$C_i$
contains an infinite ascending sequence. Now proceed as in the proof of Theorem 4.9, except notice that now the sets
![]() $W_i$
are not necessarily well-founded. What matters is that
$W_i$
are not necessarily well-founded. What matters is that
![]() $W_i$
has no maximum element and that
$W_i$
has no maximum element and that
![]() $C_i \setminus W_i$
is reverse well-founded for each
$C_i \setminus W_i$
is reverse well-founded for each
![]() $i < k$
. Relabel the chains
$i < k$
. Relabel the chains
![]() $C_0, \dots , C_{k-1}$
so that the non-empty
$C_0, \dots , C_{k-1}$
so that the non-empty
![]() $W_i$
are exactly
$W_i$
are exactly
![]() $W_0, \dots , W_{u-1}$
for some u with
$W_0, \dots , W_{u-1}$
for some u with
![]() $0 < u \leq k$
. Each
$0 < u \leq k$
. Each
![]() $W_i$
for
$W_i$
for
![]() $i < u$
is non-empty and has no maximum element. Therefore, for each
$i < u$
is non-empty and has no maximum element. Therefore, for each
![]() $i < u$
we can define an infinite ascending sequence
$i < u$
we can define an infinite ascending sequence
![]() $A_i$
in
$A_i$
in
![]() $W_i$
that is cofinal in
$W_i$
that is cofinal in
![]() $W_i$
. No tail of
$W_i$
. No tail of
![]() $A_i$
is
$A_i$
is
![]() $(0,\infty )$
-homogeneous for any
$(0,\infty )$
-homogeneous for any
![]() $i < u$
by the assumption that P does not contain a
$i < u$
by the assumption that P does not contain a
![]() $(0,\infty )$
-homogeneous chain of order-type
$(0,\infty )$
-homogeneous chain of order-type
![]() $\omega $
. As in the proof of Theorem 4.9, apply Lemma 4.8 to the sequences
$\omega $
. As in the proof of Theorem 4.9, apply Lemma 4.8 to the sequences
![]() $A_0, \dots , A_{u-1}$
to obtain infinite ascending sequences
$A_0, \dots , A_{u-1}$
to obtain infinite ascending sequences
![]() $B_0, \dots , B_{u-1}$
and a function
$B_0, \dots , B_{u-1}$
and a function
![]() $h \colon u \rightarrow k$
such that for each
$h \colon u \rightarrow k$
such that for each
![]() $i < u$
,
$i < u$
,
![]() $B_i$
is a counterexample sequence to
$B_i$
is a counterexample sequence to
![]() $A_i$
that is contained in chain
$A_i$
that is contained in chain
![]() $C_{h(i)}$
. The sequence
$C_{h(i)}$
. The sequence
![]() $B_i$
is contained in
$B_i$
is contained in
![]() $W_{h(i)}$
for each
$W_{h(i)}$
for each
![]() $i < u$
by the definition of
$i < u$
by the definition of
![]() $W_{h(i)}$
. Thus
$W_{h(i)}$
. Thus
![]() $W_{h(i)}$
is infinite for each
$W_{h(i)}$
is infinite for each
![]() $i < u$
, so
$i < u$
, so
![]() $h(i) < u$
for each
$h(i) < u$
for each
![]() $i < u$
. Therefore h is a function
$i < u$
. Therefore h is a function
![]() $h \colon u \rightarrow u$
. As in the proof of Theorem 4.9, there are
$h \colon u \rightarrow u$
. As in the proof of Theorem 4.9, there are
![]() $m < n \leq u$
with
$m < n \leq u$
with
![]() $h^m(0) = h^n(0)$
, which yields that
$h^m(0) = h^n(0)$
, which yields that
![]() $B_{h^{m+1}(0)} \leq _{\forall \exists } A_{h^{m+1}(0)}$
, which contradicts that
$B_{h^{m+1}(0)} \leq _{\forall \exists } A_{h^{m+1}(0)}$
, which contradicts that
![]() $B_{h^{m+1}(0)}$
is a counterexample sequence for
$B_{h^{m+1}(0)}$
is a counterexample sequence for
![]() $A_{h^{m+1}(0)}$
. Ultimately, we contradicted the assumption that P does not contain a
$A_{h^{m+1}(0)}$
. Ultimately, we contradicted the assumption that P does not contain a
![]() $(0,\infty )$
-homogeneous chain of order-type
$(0,\infty )$
-homogeneous chain of order-type
![]() $\omega $
. Thus P does contain a
$\omega $
. Thus P does contain a
![]() $(0,\infty )$
-homogeneous chain of order-type
$(0,\infty )$
-homogeneous chain of order-type
![]() $\omega $
, and such a chain is
$\omega $
, and such a chain is
![]() $(0,\mathrm {cof})$
-homogeneous.
$(0,\mathrm {cof})$
-homogeneous.
5 Proofs of
 $\mathsf {RSpo}_{<\infty }$
,
$\mathsf {RSpo}_{<\infty }$
,
 $\mathsf {RSpo}_k$
, and
$\mathsf {RSpo}_k$
, and
 $(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2$
in
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2$
in
 $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
and below
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
and below
The goal of this section is to show the following:
-
•
 $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash \mathsf {RSpo}_{<\infty }$
(Theorem 5.5).
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash \mathsf {RSpo}_{<\infty }$
(Theorem 5.5). -
•
 $\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {RSpo}_k$
for each fixed k (Theorem 5.6).
$\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {RSpo}_k$
for each fixed k (Theorem 5.6). -
•
 $\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {RSpo}^{\mathsf {CD}}_2$
(Theorem 5.9).
$\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {RSpo}^{\mathsf {CD}}_2$
(Theorem 5.9). -
•
 $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
(Theorem 5.11).
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
(Theorem 5.11).
The main tools used in the proof of
![]() $\mathsf {RSpo}_{<\infty }$
in
$\mathsf {RSpo}_{<\infty }$
in
![]() $\mathsf {ACA}_0$
from Theorem 4.9 are the counterexamples and counterexample sequences of Definition 4.7. Let
$\mathsf {ACA}_0$
from Theorem 4.9 are the counterexamples and counterexample sequences of Definition 4.7. Let
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in a partial order
$A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in a partial order
![]() $(P, <_P)$
such that no tail of A is
$(P, <_P)$
such that no tail of A is
![]() $(0,\infty )$
-homogeneous. Given a
$(0,\infty )$
-homogeneous. Given a
![]() $p \in P$
, p being a counterexample to a given tail of A is a
$p \in P$
, p being a counterexample to a given tail of A is a
![]() $\Pi ^0_1$
property, thus when working strictly below
$\Pi ^0_1$
property, thus when working strictly below
![]() $\mathsf {ACA}_0$
we may not necessarily be able to produce a counterexample sequence for A as in Lemma 4.8. However, given an
$\mathsf {ACA}_0$
we may not necessarily be able to produce a counterexample sequence for A as in Lemma 4.8. However, given an
![]() $a_m$
, we can effectively search for an
$a_m$
, we can effectively search for an
![]() $a_n$
and a
$a_n$
and a
![]() $p \in P$
with
$p \in P$
with
![]() $p \geq _P a_m$
and
$p \geq _P a_m$
and
![]() $p \mid _P a_n$
. This search procedure can be used to produce ladders for A according to the following definition. These ladders play the role of the counterexample sequences.
$p \mid _P a_n$
. This search procedure can be used to produce ladders for A according to the following definition. These ladders play the role of the counterexample sequences.
Definition 5.1. Let
![]() $(P, <_P)$
be a partial order, and let
$(P, <_P)$
be a partial order, and let
![]() $S = \langle s_n : n \in \mathbb {N} \rangle $
be an infinite sequence in P. An infinite ascending sequence
$S = \langle s_n : n \in \mathbb {N} \rangle $
be an infinite sequence in P. An infinite ascending sequence
![]() $B = \langle b_n : n \in \mathbb {N} \rangle $
is called a ladder for S if
$B = \langle b_n : n \in \mathbb {N} \rangle $
is called a ladder for S if
![]() $\forall n \, (s_n \leq _P b_n)$
.
$\forall n \, (s_n \leq _P b_n)$
.
In Definition 5.1, the sequence S is not required to be ascending, but in practice it usually is. Notice also that if A is an infinite ascending sequence in a partial order
![]() $(P, <_P)$
, then A is a ladder for itself.
$(P, <_P)$
, then A is a ladder for itself.
Let
![]() $(P, <_P)$
be a partial order that has been decomposed into k chains as
$(P, <_P)$
be a partial order that has been decomposed into k chains as
![]() $P = C_0 \cup \cdots \cup C_{k-1}$
, and let
$P = C_0 \cup \cdots \cup C_{k-1}$
, and let
![]() $\vec {P}$
denote
$\vec {P}$
denote
![]() $\vec {P} = P \oplus {<_P} \oplus C_0 \oplus \cdots \oplus C_{k-1}$
. Suppose that A is an infinite ascending sequence that is contained in some chain
$\vec {P} = P \oplus {<_P} \oplus C_0 \oplus \cdots \oplus C_{k-1}$
. Suppose that A is an infinite ascending sequence that is contained in some chain
![]() $C_j$
. To produce a
$C_j$
. To produce a
![]() $(0,\infty )$
-homogeneous chain for P, we look for ladders for A in the chains
$(0,\infty )$
-homogeneous chain for P, we look for ladders for A in the chains
![]() $C_i$
with
$C_i$
with
![]() $i \neq j$
. To do this, we define a Turing functional
$i \neq j$
. To do this, we define a Turing functional
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \times k \rightarrow P^{\mathbb {N}}$
relative to
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \times k \rightarrow P^{\mathbb {N}}$
relative to
![]() $\vec {P}$
, where
$\vec {P}$
, where
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
attempts to compute a ladder for A in
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
attempts to compute a ladder for A in
![]() $C_i$
. We then use
$C_i$
. We then use
![]() $\mathsf {I}\Sigma ^0_{2}$
in the form of bounded
$\mathsf {I}\Sigma ^0_{2}$
in the form of bounded
![]() $\Pi ^0_2$
comprehension to determine the
$\Pi ^0_2$
comprehension to determine the
![]() $i < k$
with
$i < k$
with
![]() $i \neq j$
for which
$i \neq j$
for which
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total. If
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total. If
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total, we then want to find ladders for it in the chains
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total, we then want to find ladders for it in the chains
![]() $C_{\ell }$
with
$C_{\ell }$
with
![]() $\ell \neq i$
and continue this process either until finding enough ladders to knit together into a
$\ell \neq i$
and continue this process either until finding enough ladders to knit together into a
![]() $(0,\infty )$
-homogeneous chain or until realizing that there are so few ladders that a tail of one of them must already be
$(0,\infty )$
-homogeneous chain or until realizing that there are so few ladders that a tail of one of them must already be
![]() $(0,\infty )$
-homogeneous. In fact, we consider all the iterations of
$(0,\infty )$
-homogeneous. In fact, we consider all the iterations of
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}$
that we may eventually need up front and apply bounded
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}$
that we may eventually need up front and apply bounded
![]() $\Pi ^0_2$
comprehension only once.
$\Pi ^0_2$
comprehension only once.
Lemma 5.2 says that if
![]() $(P, <_P)$
is a partial order decomposed into chains
$(P, <_P)$
is a partial order decomposed into chains
![]() $C_0, \dots , C_{k-1}$
and A is an infinite ascending sequence in P with no
$C_0, \dots , C_{k-1}$
and A is an infinite ascending sequence in P with no
![]() $(0,\infty )$
-homogeneous tail, then it is possible to search for a ladder for A in some
$(0,\infty )$
-homogeneous tail, then it is possible to search for a ladder for A in some
![]() $C_i$
.
$C_i$
.
Lemma 5.2. The following is provable in
![]() $\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_{2}$
. Let
$\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_{2}$
. Let
![]() $(P, <_P)$
be an infinite partial order with k-chain decomposition
$(P, <_P)$
be an infinite partial order with k-chain decomposition
![]() $C_0, \dots , C_{k-1}$
, and let
$C_0, \dots , C_{k-1}$
, and let
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in P. If no tail of A is
$A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in P. If no tail of A is
![]() $(0,\infty )$
-homogeneous, then there is an
$(0,\infty )$
-homogeneous, then there is an
![]() $i < k$
such that
$i < k$
such that
Proof Suppose that no tail
![]() $A_{\geq m}$
of A is
$A_{\geq m}$
of A is
![]() $(0,\infty )$
-homogeneous. Then for every m, there is a counterexample p to the tail
$(0,\infty )$
-homogeneous. Then for every m, there is a counterexample p to the tail
![]() $A_{\geq m}$
. This implies that
$A_{\geq m}$
. This implies that
Thus we may define a function
![]() $f \colon \mathbb {N} \rightarrow k$
as follows. Given m, search for an n and a p with
$f \colon \mathbb {N} \rightarrow k$
as follows. Given m, search for an n and a p with
![]() $p \geq _P a_m$
and
$p \geq _P a_m$
and
![]() $p \mid _P a_n$
, find the
$p \mid _P a_n$
, find the
![]() $i < k$
with
$i < k$
with
![]() $p \in C_i$
, and output
$p \in C_i$
, and output
![]() $f(m) = i$
. By
$f(m) = i$
. By
![]() $\mathsf {RT}^1_{<\infty }$
, there is an
$\mathsf {RT}^1_{<\infty }$
, there is an
![]() $i < k$
such that
$i < k$
such that
![]() $f(m) = i$
for infinitely many m. This i satisfies the conclusion of the lemma.
$f(m) = i$
for infinitely many m. This i satisfies the conclusion of the lemma.
Again let
![]() $(P, <_P)$
be a partial order with k-chain decomposition
$(P, <_P)$
be a partial order with k-chain decomposition
![]() $C_0, \dots , C_{k-1}$
. Lemma 5.3 shows how to search for a ladder for a given infinite sequence A within a target chain
$C_0, \dots , C_{k-1}$
. Lemma 5.3 shows how to search for a ladder for a given infinite sequence A within a target chain
![]() $C_i$
. It may be thought of as a weaker, yet effective, version of Lemma 4.8.
$C_i$
. It may be thought of as a weaker, yet effective, version of Lemma 4.8.
Lemma 5.3. The following is provable in
![]() $\mathsf {RCA}_0$
. Let
$\mathsf {RCA}_0$
. Let
![]() $(P, <_P)$
be a partial order with k-chain decomposition
$(P, <_P)$
be a partial order with k-chain decomposition
![]() $C_0, \dots , C_{k-1}$
. Let
$C_0, \dots , C_{k-1}$
. Let
![]() $\vec {P}$
denote
$\vec {P}$
denote
![]() $\vec {P} = P \oplus {<_P} \oplus C_0 \oplus \cdots \oplus C_{k-1}$
. Then there is a Turing functional
$\vec {P} = P \oplus {<_P} \oplus C_0 \oplus \cdots \oplus C_{k-1}$
. Then there is a Turing functional
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \times k \rightarrow P^{\mathbb {N}}$
relative to
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \times k \rightarrow P^{\mathbb {N}}$
relative to
![]() $\vec {P}$
with the following properties for every infinite sequence
$\vec {P}$
with the following properties for every infinite sequence
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
in P and every
$A = \langle a_n : n \in \mathbb {N} \rangle $
in P and every
![]() $i < k$
.
$i < k$
.
-
(1) If
 $$ \begin{align*} \forall m \; \exists n \; \exists p \in C_i \; \bigl(p \geq_P a_m \;\wedge\; p \mid_P a_n\bigr), \end{align*} $$
$$ \begin{align*} \forall m \; \exists n \; \exists p \in C_i \; \bigl(p \geq_P a_m \;\wedge\; p \mid_P a_n\bigr), \end{align*} $$
then
 $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total. -
(2) If
 $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total, then it computes a ladder for A in
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total, then it computes a ladder for A in
 $C_i$
.
$C_i$
.
Proof Let
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite sequence in P, and let
$A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite sequence in P, and let
![]() $i < k$
. Compute
$i < k$
. Compute
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(0)$
by searching for an n and a
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(0)$
by searching for an n and a
![]() $p_0 \in C_i$
with
$p_0 \in C_i$
with
![]() $p_0 \geq _P a_0$
and
$p_0 \geq _P a_0$
and
![]() $p_0 \mid _P a_n$
. If
$p_0 \mid _P a_n$
. If
![]() $p_0$
is found, then output
$p_0$
is found, then output
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(0) = p_0$
. Compute
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(0) = p_0$
. Compute
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m+1)$
by first computing
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m+1)$
by first computing
![]() $p_m = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m)$
. Then search for an n and a
$p_m = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m)$
. Then search for an n and a
![]() $p_{m+1} \in C_i$
with
$p_{m+1} \in C_i$
with
![]() $p_{m+1}>_P p_m$
,
$p_{m+1}>_P p_m$
,
![]() $p_{m+1} \geq _P a_{m+1}$
, and
$p_{m+1} \geq _P a_{m+1}$
, and
![]() $p_{m+1} \mid _P a_n$
. If
$p_{m+1} \mid _P a_n$
. If
![]() $p_{m+1}$
is found, then output
$p_{m+1}$
is found, then output
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m+1) = p_{m+1}$
.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m+1) = p_{m+1}$
.
Item (2) follows immediately from the definition of
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}$
. If
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}$
. If
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
is an infinite sequence in P, if
$A = \langle a_n : n \in \mathbb {N} \rangle $
is an infinite sequence in P, if
![]() $i < k$
, and if
$i < k$
, and if
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total, then it must be that
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total, then it must be that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m) \in C_i$
, that
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m) \in C_i$
, that
![]() $a_m \leq _P \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m)$
, and that
$a_m \leq _P \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m)$
, and that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m) <_P \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m+1)$
for every m.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m) <_P \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m+1)$
for every m.
For item (1), let
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite sequence in P, let
$A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite sequence in P, let
![]() $i < k$
, and suppose that for every m there are an n and a
$i < k$
, and suppose that for every m there are an n and a
![]() $p \in C_i$
with
$p \in C_i$
with
![]() $p \geq _P a_m$
and
$p \geq _P a_m$
and
![]() $p \mid _P a_n$
. We use
$p \mid _P a_n$
. We use
![]() $\mathsf {I}\Sigma ^0_{1}$
to show that
$\mathsf {I}\Sigma ^0_{1}$
to show that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total. By assumption, there are an n and a
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)$
is total. By assumption, there are an n and a
![]() $p_0 \in C_i$
with
$p_0 \in C_i$
with
![]() $p_0 \geq _P a_0$
and
$p_0 \geq _P a_0$
and
![]() $p_0 \mid _P a_n$
. Thus
$p_0 \mid _P a_n$
. Thus
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(0)$
is defined. Inductively assume that
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(0)$
is defined. Inductively assume that
![]() $p_m = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m)$
is defined. Then there is an
$p_m = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m)$
is defined. Then there is an
![]() $\ell $
such that
$\ell $
such that
![]() $p_m \mid _P a_{\ell }$
. By assumption, there are an s and a
$p_m \mid _P a_{\ell }$
. By assumption, there are an s and a
![]() $p \in C_i$
with
$p \in C_i$
with
and also a t and a
![]() $q \in C_i$
with
$q \in C_i$
with
The elements p and q are both in the chain
![]() $C_i$
, so they are comparable. By taking
$C_i$
, so they are comparable. By taking
![]() $p_{m+1} = \max _{<_P}\{p, q\}$
and n as either s or t as appropriate, we obtain an n and a
$p_{m+1} = \max _{<_P}\{p, q\}$
and n as either s or t as appropriate, we obtain an n and a
![]() $p_{m+1} \in C_i$
with
$p_{m+1} \in C_i$
with
Again,
![]() $p_{m+1}$
and
$p_{m+1}$
and
![]() $p_m$
are both in the chain
$p_m$
are both in the chain
![]() $C_i$
, so they are comparable. However, we cannot have that
$C_i$
, so they are comparable. However, we cannot have that
![]() $p_{m+1} \leq _P p_m$
because this would imply that
$p_{m+1} \leq _P p_m$
because this would imply that
![]() $a_{\ell } \leq _P p_{m+1} \leq _P p_m$
, which contradicts that
$a_{\ell } \leq _P p_{m+1} \leq _P p_m$
, which contradicts that
![]() $p_m \mid _P a_{\ell }$
. Therefore
$p_m \mid _P a_{\ell }$
. Therefore
![]() $p_m <_P p_{m+1}$
. Thus there are an n and a
$p_m <_P p_{m+1}$
. Thus there are an n and a
![]() $p_{m+1} \in C_i$
with
$p_{m+1} \in C_i$
with
![]() $p_{m+1}>_P p_m$
,
$p_{m+1}>_P p_m$
,
![]() $p_{m+1} \geq _P a_{m+1}$
, and
$p_{m+1} \geq _P a_{m+1}$
, and
![]() $p_{m+1} \mid _P a_n$
. So
$p_{m+1} \mid _P a_n$
. So
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m+1)$
is defined.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, i)(m+1)$
is defined.
The following lemma concerning finite labeled trees helps organize the proof of
![]() $\mathsf {RSpo}_{<\infty }$
in
$\mathsf {RSpo}_{<\infty }$
in
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
. Recall that for a finite rooted tree T, the height of a vertex is the length of the path from the vertex to the root, the height of the tree is the maximum height of a vertex in T, and level k of T consists of all the vertices of T that have height k. (We warn the reader that the height of a tree as defined here is one less than the height of the tree according to Definition 3.1 when considering the tree as a partial order. For example, the one-element tree consisting of only the root has height
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
. Recall that for a finite rooted tree T, the height of a vertex is the length of the path from the vertex to the root, the height of the tree is the maximum height of a vertex in T, and level k of T consists of all the vertices of T that have height k. (We warn the reader that the height of a tree as defined here is one less than the height of the tree according to Definition 3.1 when considering the tree as a partial order. For example, the one-element tree consisting of only the root has height
![]() $0$
as a tree but height
$0$
as a tree but height
![]() $1$
as a partial order.) For a rooted tree T, let
$1$
as a partial order.) For a rooted tree T, let
![]() $\preceq $
denote the associated tree-order on T, where
$\preceq $
denote the associated tree-order on T, where
![]() $\sigma \preceq \tau $
if
$\sigma \preceq \tau $
if
![]() $\sigma $
is on the (unique) path from the root to
$\sigma $
is on the (unique) path from the root to
![]() $\tau $
. Let
$\tau $
. Let
![]() $\prec $
denote the strict version of
$\prec $
denote the strict version of
![]() $\preceq $
.
$\preceq $
.
Lemma 5.4. The following is provable in
![]() $\mathsf {RCA}_0$
. Let
$\mathsf {RCA}_0$
. Let
![]() $k \geq 2$
, and let T be a finite rooted tree with the following properties.
$k \geq 2$
, and let T be a finite rooted tree with the following properties.
-
• T has height k.
-
• Every leaf of T is at level k.
-
• The vertices of T are labeled by a function
 $\ell \colon T \rightarrow k$
in such a way that if
$\ell \colon T \rightarrow k$
in such a way that if
 $\sigma \in T$
is not a leaf and
$\sigma \in T$
is not a leaf and
 $\tau _0, \dots , \tau _{n-1}$
are the children of
$\tau _0, \dots , \tau _{n-1}$
are the children of
 $\sigma $
, then
$\sigma $
, then
 $\ell (\tau _0), \dots , \ell (\tau _{n-1})$
are distinct elements of
$\ell (\tau _0), \dots , \ell (\tau _{n-1})$
are distinct elements of
 $k \setminus \{\ell (\sigma )\}$
.
$k \setminus \{\ell (\sigma )\}$
.
Then there is a
![]() $\sigma \in T$
that is not a leaf such that for every child
$\sigma \in T$
that is not a leaf such that for every child
![]() $\tau $
of
$\tau $
of
![]() $\sigma $
there is an
$\sigma $
there is an
![]() $\eta \succ \tau $
with
$\eta \succ \tau $
with
![]() $\ell (\eta ) = \ell (\sigma )$
.
$\ell (\eta ) = \ell (\sigma )$
.
Proof Proceed by
![]() $\Pi ^0_1$
induction on
$\Pi ^0_1$
induction on
![]() $k \geq 2$
. For the base case
$k \geq 2$
. For the base case
![]() $k = 2$
, the only possibility for T is a path of length
$k = 2$
, the only possibility for T is a path of length
![]() $2$
consisting of the root r, r’s child
$2$
consisting of the root r, r’s child
![]() $\tau $
, and
$\tau $
, and
![]() $\tau $
’s child
$\tau $
’s child
![]() $\eta $
, where
$\eta $
, where
![]() $\ell (r) \neq \ell (\tau )$
and
$\ell (r) \neq \ell (\tau )$
and
![]() $\ell (\tau ) \neq \ell (\eta )$
. As
$\ell (\tau ) \neq \ell (\eta )$
. As
![]() $k = 2$
, it must be that
$k = 2$
, it must be that
![]() $\ell (r) = \ell (\eta )$
, so we may take
$\ell (r) = \ell (\eta )$
, so we may take
![]() $\sigma = r$
.
$\sigma = r$
.
Now suppose that the lemma holds for k. Consider a tree T of height
![]() $k+1$
where every leaf is at level
$k+1$
where every leaf is at level
![]() $k+1$
, and consider also a labeling
$k+1$
, and consider also a labeling
![]() $\ell \colon T \rightarrow k+1$
that labels T according to the hypothesis of the lemma. Let r be the root, and let
$\ell \colon T \rightarrow k+1$
that labels T according to the hypothesis of the lemma. Let r be the root, and let
![]() $\tau _0, \dots , \tau _{n-1}$
be r’s children. If for every
$\tau _0, \dots , \tau _{n-1}$
be r’s children. If for every
![]() $\tau _i$
there is an
$\tau _i$
there is an
![]() $\eta \succ \tau _i$
with
$\eta \succ \tau _i$
with
![]() $\ell (\eta ) = \ell (r)$
, then we may take
$\ell (\eta ) = \ell (r)$
, then we may take
![]() $\sigma = r$
. Otherwise, there is a
$\sigma = r$
. Otherwise, there is a
![]() $\tau _i$
such that no
$\tau _i$
such that no
![]() $\eta \succ \tau _i$
has
$\eta \succ \tau _i$
has
![]() $\ell (\eta ) = \ell (r)$
. Let
$\ell (\eta ) = \ell (r)$
. Let
![]() $S = \{\eta \in T : \eta \succeq \tau _i\}$
be the complete subtree of T above
$S = \{\eta \in T : \eta \succeq \tau _i\}$
be the complete subtree of T above
![]() $\tau _i$
rooted at
$\tau _i$
rooted at
![]() $\tau _i$
. Then S has height k, and every leaf of S is at level k of S. Moreover, S is labeled by
$\tau _i$
. Then S has height k, and every leaf of S is at level k of S. Moreover, S is labeled by
![]() $\ell $
, which only uses labels from the set
$\ell $
, which only uses labels from the set
![]() $(k+1) \setminus \{\ell (r)\}$
. Fix a bijection
$(k+1) \setminus \{\ell (r)\}$
. Fix a bijection
![]() $f \colon (k+1) \setminus \{\ell (r)\} \rightarrow k$
, and define the labeling
$f \colon (k+1) \setminus \{\ell (r)\} \rightarrow k$
, and define the labeling
![]() $\widehat {\ell } \colon S \rightarrow k$
by
$\widehat {\ell } \colon S \rightarrow k$
by
![]() $\widehat {\ell } = f \circ \ell $
. By the induction hypothesis applied to S and
$\widehat {\ell } = f \circ \ell $
. By the induction hypothesis applied to S and
![]() $\widehat {\ell }$
, there is a
$\widehat {\ell }$
, there is a
![]() $\sigma \in S$
that is not a leaf such that for every child
$\sigma \in S$
that is not a leaf such that for every child
![]() $\tau $
of
$\tau $
of
![]() $\sigma $
in S there is an
$\sigma $
in S there is an
![]() $\eta \succ \tau $
in S with
$\eta \succ \tau $
in S with
![]() $\widehat {\ell }(\eta ) = \widehat {\ell }(\sigma )$
. This
$\widehat {\ell }(\eta ) = \widehat {\ell }(\sigma )$
. This
![]() $\sigma $
also satisfies the conclusion of the lemma for T because S is the complete subtree of T above
$\sigma $
also satisfies the conclusion of the lemma for T because S is the complete subtree of T above
![]() $\tau _i$
: for every child
$\tau _i$
: for every child
![]() $\tau $
of
$\tau $
of
![]() $\sigma $
in T, there is an
$\sigma $
in T, there is an
![]() $\eta \succ \tau $
in T with
$\eta \succ \tau $
in T with
![]() $\widehat {\ell }(\eta ) = \widehat {\ell }(\sigma )$
and hence with
$\widehat {\ell }(\eta ) = \widehat {\ell }(\sigma )$
and hence with
![]() $\ell (\eta ) = \ell (\sigma )$
.
$\ell (\eta ) = \ell (\sigma )$
.
Theorem 5.5.
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash \mathsf {RSpo}_{<\infty }$
.
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash \mathsf {RSpo}_{<\infty }$
.
Proof It suffices to show that
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash \mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
because
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash \mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
because
![]() $\mathsf {RSpo}_{<\infty }$
and
$\mathsf {RSpo}_{<\infty }$
and
![]() $\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
are equivalent over
$\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
are equivalent over
![]() $\mathsf {RCA}_0$
as explained in Section 3. Thus let
$\mathsf {RCA}_0$
as explained in Section 3. Thus let
![]() $(P, <_P)$
be an infinite partial order with k-chain decomposition
$(P, <_P)$
be an infinite partial order with k-chain decomposition
![]() $C_0, \dots , C_{k-1}$
for some k. We may assume that
$C_0, \dots , C_{k-1}$
for some k. We may assume that
![]() $k \geq 2$
because if P is a chain, then P itself is
$k \geq 2$
because if P is a chain, then P itself is
![]() $(0,\infty )$
-homogeneous.
$(0,\infty )$
-homogeneous.
Some
![]() $C_i$
is infinite by
$C_i$
is infinite by
![]() $\mathsf {RT}^1_{<\infty }$
and therefore contains either an infinite ascending sequence or an infinite descending sequence by
$\mathsf {RT}^1_{<\infty }$
and therefore contains either an infinite ascending sequence or an infinite descending sequence by
![]() $\mathsf {ADS}$
. By relabeling the chains and by reversing the partial order if necessary, we may assume that there is an infinite ascending sequence
$\mathsf {ADS}$
. By relabeling the chains and by reversing the partial order if necessary, we may assume that there is an infinite ascending sequence
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
contained in chain
$A = \langle a_n : n \in \mathbb {N} \rangle $
contained in chain
![]() $C_0$
. Let
$C_0$
. Let
![]() $\vec {P} = P \oplus {<_P} \oplus C_0 \oplus \cdots \oplus C_{k-1}$
, and let
$\vec {P} = P \oplus {<_P} \oplus C_0 \oplus \cdots \oplus C_{k-1}$
, and let
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \times k \rightarrow P^{\mathbb {N}}$
be the Turing functional relative to
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \times k \rightarrow P^{\mathbb {N}}$
be the Turing functional relative to
![]() $\vec {P}$
from Lemma 5.3.
$\vec {P}$
from Lemma 5.3.
Let
![]() $R = (k-1)^{\leq k}$
be the complete
$R = (k-1)^{\leq k}$
be the complete
![]() $(k-1)$
-ary tree of height k. Assign a label
$(k-1)$
-ary tree of height k. Assign a label
![]() $\ell (\sigma ) \in \{0, \dots , k-1\}$
to each
$\ell (\sigma ) \in \{0, \dots , k-1\}$
to each
![]() $\sigma \in R$
as follows. First, label the root
$\sigma \in R$
as follows. First, label the root
![]() $\emptyset \in R$
with
$\emptyset \in R$
with
![]() $\ell (\emptyset ) = 0$
. Now suppose that
$\ell (\emptyset ) = 0$
. Now suppose that
![]() $\sigma \in R$
is not a leaf and has been labeled
$\sigma \in R$
is not a leaf and has been labeled
![]() $\ell (\sigma )$
. Index the
$\ell (\sigma )$
. Index the
![]() $k-1$
children of
$k-1$
children of
![]() $\sigma $
as
$\sigma $
as
![]() $\langle \tau _i : i \in k \setminus \{\ell (\sigma )\} \rangle $
, and label
$\langle \tau _i : i \in k \setminus \{\ell (\sigma )\} \rangle $
, and label
![]() $\ell (\tau _i) = i$
for each
$\ell (\tau _i) = i$
for each
![]() $i \in k \setminus \{\ell (\sigma )\}$
.
$i \in k \setminus \{\ell (\sigma )\}$
.
For a
![]() $\sigma \in \mathbb {N}^{<\mathbb {N}}$
with
$\sigma \in \mathbb {N}^{<\mathbb {N}}$
with
![]() $|\sigma | \geq 1$
, let
$|\sigma | \geq 1$
, let
![]() $\sigma ^- = \sigma {\restriction } (|\sigma |-1)$
denote
$\sigma ^- = \sigma {\restriction } (|\sigma |-1)$
denote
![]() $\sigma $
with the last term cut off. For
$\sigma $
with the last term cut off. For
![]() $\sigma \in R$
, let
$\sigma \in R$
, let
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P},\sigma }$
denote the iteration of
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P},\sigma }$
denote the iteration of
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}$
given by
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}$
given by
 $$ \begin{align*} \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \emptyset}(A) &= A,\\ \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \sigma}(A) &= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \sigma^-}(A), \ell(\sigma)), & \text{if } |\sigma| \geq 1. \end{align*} $$
$$ \begin{align*} \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \emptyset}(A) &= A,\\ \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \sigma}(A) &= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \sigma^-}(A), \ell(\sigma)), & \text{if } |\sigma| \geq 1. \end{align*} $$
So if
![]() $\sigma \in R$
has
$\sigma \in R$
has
![]() $|\sigma | \geq 1$
, then
$|\sigma | \geq 1$
, then
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
is
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
is
Now use
![]() $\mathsf {I}\Sigma ^0_{2}$
in the form of bounded
$\mathsf {I}\Sigma ^0_{2}$
in the form of bounded
![]() $\Pi ^0_2$
comprehension to form the subtree
$\Pi ^0_2$
comprehension to form the subtree
![]() $T \subseteq R$
given by
$T \subseteq R$
given by
Notice that if
![]() $\sigma $
is in T, then
$\sigma $
is in T, then
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes an infinite ascending sequence in
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes an infinite ascending sequence in
![]() $C_{\ell (\sigma )}$
by Lemma 5.3 item (2) and the fact that A is an infinite ascending sequence in
$C_{\ell (\sigma )}$
by Lemma 5.3 item (2) and the fact that A is an infinite ascending sequence in
![]() $C_0 = C_{\ell (\emptyset )}$
.
$C_0 = C_{\ell (\emptyset )}$
.
There are now two cases. The first case is that T has a leaf
![]() $\sigma $
at some level
$\sigma $
at some level
![]() $<\! k$
. Let
$<\! k$
. Let
![]() $\langle \tau _i : i \in k \setminus \{\ell (\sigma )\} \rangle $
again denote the indexing of
$\langle \tau _i : i \in k \setminus \{\ell (\sigma )\} \rangle $
again denote the indexing of
![]() $\sigma $
’s children in R. As
$\sigma $
’s children in R. As
![]() $\sigma $
is in T,
$\sigma $
is in T,
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes the infinite ascending sequence
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes the infinite ascending sequence
![]() $B = \langle b_n : n \in \mathbb {N} \rangle $
in
$B = \langle b_n : n \in \mathbb {N} \rangle $
in
![]() $C_{\ell (\sigma )}$
given by
$C_{\ell (\sigma )}$
given by
![]() $b_n = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)(n)$
for all n. If no tail of B is
$b_n = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)(n)$
for all n. If no tail of B is
![]() $(0,\infty )$
-homogeneous, then by Lemma 5.2 there is an
$(0,\infty )$
-homogeneous, then by Lemma 5.2 there is an
![]() $i < k$
such that
$i < k$
such that
It cannot be that
![]() $i = \ell (\sigma )$
, so there must be such an
$i = \ell (\sigma )$
, so there must be such an
![]() $i \in k \setminus \{\ell (\sigma )\}$
. Thus, by Lemma 5.3 item (1),
$i \in k \setminus \{\ell (\sigma )\}$
. Thus, by Lemma 5.3 item (1),
is total. This means that
![]() $\tau _i \in T$
, which contradicts that
$\tau _i \in T$
, which contradicts that
![]() $\sigma $
is a leaf of T. Therefore some tail of B is indeed
$\sigma $
is a leaf of T. Therefore some tail of B is indeed
![]() $(0,\infty )$
-homogeneous. We may thin this tail so that its range exists as a set, thereby producing a
$(0,\infty )$
-homogeneous. We may thin this tail so that its range exists as a set, thereby producing a
![]() $(0,\infty )$
-homogeneous chain in P.
$(0,\infty )$
-homogeneous chain in P.
The second case is that every leaf of T is at level k. Then T and
![]() $\ell $
satisfy the hypotheses of Lemma 5.4. Let
$\ell $
satisfy the hypotheses of Lemma 5.4. Let
![]() $\sigma $
be as in the conclusion of Lemma 5.4 for T and
$\sigma $
be as in the conclusion of Lemma 5.4 for T and
![]() $\ell $
. For each child
$\ell $
. For each child
![]() $\tau $
of
$\tau $
of
![]() $\sigma $
in T, let
$\sigma $
in T, let
![]() $\eta _{\tau } \in T$
be such that
$\eta _{\tau } \in T$
be such that
![]() $\eta _{\tau } \succ \tau $
and
$\eta _{\tau } \succ \tau $
and
![]() $\ell (\eta _{\tau }) = \ell (\sigma )$
. As
$\ell (\eta _{\tau }) = \ell (\sigma )$
. As
![]() $\sigma \in T$
,
$\sigma \in T$
,
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes the infinite ascending sequence
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes the infinite ascending sequence
![]() $X = \langle x_n : n \in \mathbb {N} \rangle $
in
$X = \langle x_n : n \in \mathbb {N} \rangle $
in
![]() $C_{\ell (\sigma )}$
given by
$C_{\ell (\sigma )}$
given by
![]() $x_n = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)(n)$
for all n. Likewise,
$x_n = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)(n)$
for all n. Likewise,
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \eta _{\tau }}(A)$
also computes an infinite ascending sequence in
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \eta _{\tau }}(A)$
also computes an infinite ascending sequence in
![]() $C_{\ell (\eta _{\tau })} = C_{\ell (\sigma )}$
for each child
$C_{\ell (\eta _{\tau })} = C_{\ell (\sigma )}$
for each child
![]() $\tau $
of
$\tau $
of
![]() $\sigma $
in T. Define the infinite sequence
$\sigma $
in T. Define the infinite sequence
![]() $Y = \langle y_n : n \in \mathbb {N} \rangle $
by setting
$Y = \langle y_n : n \in \mathbb {N} \rangle $
by setting
for each n. Then Y is an infinite ascending sequence in
![]() $C_{\ell (\sigma )}$
that is cofinal in the union of the sequences computed by the
$C_{\ell (\sigma )}$
that is cofinal in the union of the sequences computed by the
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \eta _{\tau }}(A)$
for the children
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \eta _{\tau }}(A)$
for the children
![]() $\tau $
of
$\tau $
of
![]() $\sigma $
in T.
$\sigma $
in T.
Claim 1. Let
![]() $\tau $
be a child of
$\tau $
be a child of
![]() $\sigma $
in T. Then every
$\sigma $
in T. Then every
![]() $p \in C_{\ell (\tau )}$
is either above every element of X or below some element of Y (and hence below almost every element of Y).
$p \in C_{\ell (\tau )}$
is either above every element of X or below some element of Y (and hence below almost every element of Y).
Proof of Claim
We have that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes the infinite ascending sequence X and that
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes the infinite ascending sequence X and that
 $$ \begin{align*} \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \tau}(A) &= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \sigma}(A), \ell(\tau)) \\&= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(X, \ell(\tau)) \end{align*} $$
$$ \begin{align*} \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \tau}(A) &= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \sigma}(A), \ell(\tau)) \\&= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(X, \ell(\tau)) \end{align*} $$
is total, so
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \tau }(A)$
computes a ladder Z for X in
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \tau }(A)$
computes a ladder Z for X in
![]() $C_{\ell (\tau )}$
. Consider any
$C_{\ell (\tau )}$
. Consider any
![]() $p \in C_{\ell (\tau )}$
and its location with respect to the elements of Z. If p is above every element of Z, then p is above every element of X because Z is a ladder for X. Suppose instead that p is below some element
$p \in C_{\ell (\tau )}$
and its location with respect to the elements of Z. If p is above every element of Z, then p is above every element of X because Z is a ladder for X. Suppose instead that p is below some element
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \tau }(A)(n)$
of Z. Consider now the path
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \tau }(A)(n)$
of Z. Consider now the path
![]() $\tau = \alpha _0 \prec \alpha _1 \prec \cdots \prec \alpha _{m-1} = \eta _{\tau }$
from
$\tau = \alpha _0 \prec \alpha _1 \prec \cdots \prec \alpha _{m-1} = \eta _{\tau }$
from
![]() $\tau $
to
$\tau $
to
![]() $\eta _{\tau }$
in T. For each
$\eta _{\tau }$
in T. For each
![]() $i < m$
,
$i < m$
,
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \alpha _i}(A)$
is total because
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \alpha _i}(A)$
is total because
![]() $\alpha _i \in T$
. Thus
$\alpha _i \in T$
. Thus
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \alpha _{i+1}}(A)$
computes a ladder for
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \alpha _{i+1}}(A)$
computes a ladder for
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \alpha _i}(A)$
for each
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \alpha _i}(A)$
for each
![]() $i < m-1$
. Therefore,
$i < m-1$
. Therefore,
 $$ \begin{align*} p &\leq_P \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \tau}(A)(n) \leq_P \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \alpha_1}(A)(n) \leq_P \cdots \\ &\leq_P \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \alpha_{m-2}}(A)(n)\leq_P \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \eta_{\tau}}(A)(n) \leq_P y_n. \end{align*} $$
$$ \begin{align*} p &\leq_P \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \tau}(A)(n) \leq_P \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \alpha_1}(A)(n) \leq_P \cdots \\ &\leq_P \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \alpha_{m-2}}(A)(n)\leq_P \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \eta_{\tau}}(A)(n) \leq_P y_n. \end{align*} $$
So p is below an element of Y.
Claim 2. There is an m such that whenever
![]() $i \in k \setminus \bigl (\{\ell (\sigma )\} \cup \{\ell (\tau ) : \tau \text { is a child of } \sigma \text { in } T\}\bigr )$
and
$i \in k \setminus \bigl (\{\ell (\sigma )\} \cup \{\ell (\tau ) : \tau \text { is a child of } \sigma \text { in } T\}\bigr )$
and
![]() $p \in C_i$
, then either p is comparable with almost every element of
$p \in C_i$
, then either p is comparable with almost every element of
![]() $X_{\geq m}$
, or p is incomparable with every element of
$X_{\geq m}$
, or p is incomparable with every element of
![]() $X_{\geq m}$
.
$X_{\geq m}$
.
Proof of Claim
Let I denote the finite set
let
![]() $i \in I$
, let
$i \in I$
, let
![]() $\tau $
be the child of
$\tau $
be the child of
![]() $\sigma $
in R with
$\sigma $
in R with
![]() $\ell (\tau ) = i$
, and notice that
$\ell (\tau ) = i$
, and notice that
![]() $\tau \notin T$
. We have that
$\tau \notin T$
. We have that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes the infinite ascending sequence X, so
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, \sigma }(A)$
computes the infinite ascending sequence X, so
 $$ \begin{align*} \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \tau}(A) &= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \sigma}(A), \ell(\tau)) \\&= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(X, \ell(\tau)) \end{align*} $$
$$ \begin{align*} \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \tau}(A) &= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}, \sigma}(A), \ell(\tau)) \\&= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(X, \ell(\tau)) \end{align*} $$
must not be total because otherwise
![]() $\tau $
would be in T. Therefore by Lemma 5.3 item (1),
$\tau $
would be in T. Therefore by Lemma 5.3 item (1),
By applying
![]() $\mathsf {B}\Sigma ^0_{2}$
, we obtain a fixed m such that
$\mathsf {B}\Sigma ^0_{2}$
, we obtain a fixed m such that
![]() $\forall i \in I \; \forall n \; \forall p \in C_i \; (p \ngeq _P x_m \vee p \lessgtr _P x_n )$
. We show that this m satisfies the claim.
$\forall i \in I \; \forall n \; \forall p \in C_i \; (p \ngeq _P x_m \vee p \lessgtr _P x_n )$
. We show that this m satisfies the claim.
Let
![]() $p \in C_i$
for an
$p \in C_i$
for an
![]() $i \in I$
. If p is below an element of
$i \in I$
. If p is below an element of
![]() $X_{\geq m}$
, then p is below almost every element of
$X_{\geq m}$
, then p is below almost every element of
![]() $X_{\geq m}$
because
$X_{\geq m}$
because
![]() $X_{\geq m}$
is an ascending sequence. If p is above an element of
$X_{\geq m}$
is an ascending sequence. If p is above an element of
![]() $X_{\geq m}$
, then
$X_{\geq m}$
, then
![]() $p \geq _P x_m$
, in which case p is comparable with every element of
$p \geq _P x_m$
, in which case p is comparable with every element of
![]() $X_{\geq m}$
. So if p is comparable with some element of
$X_{\geq m}$
. So if p is comparable with some element of
![]() $X_{\geq m}$
, then p is comparable with almost every element of
$X_{\geq m}$
, then p is comparable with almost every element of
![]() $X_{\geq m}$
. That is, either p is comparable with almost every element of
$X_{\geq m}$
. That is, either p is comparable with almost every element of
![]() $X_{\geq m}$
, or p is incomparable with every element of
$X_{\geq m}$
, or p is incomparable with every element of
![]() $X_{\geq m}$
.
$X_{\geq m}$
.
We can now assemble a
![]() $(0,\infty )$
-homogeneous chain B from X and Y. Let m be as in Claim 2. Thin the infinite ascending sequences
$(0,\infty )$
-homogeneous chain B from X and Y. Let m be as in Claim 2. Thin the infinite ascending sequences
![]() $X_{\geq m}$
and Y to infinite ascending sequences
$X_{\geq m}$
and Y to infinite ascending sequences
![]() $\widehat {X}_{\geq m}$
and
$\widehat {X}_{\geq m}$
and
![]() $\widehat {Y}$
whose ranges exist as sets. Notice that
$\widehat {Y}$
whose ranges exist as sets. Notice that
![]() $\widehat {X}_{\geq m} \cup \widehat {Y}$
is a chain because
$\widehat {X}_{\geq m} \cup \widehat {Y}$
is a chain because
![]() $\widehat {X}_{\geq m}$
and
$\widehat {X}_{\geq m}$
and
![]() $\widehat {Y}$
are both contained in the chain
$\widehat {Y}$
are both contained in the chain
![]() $C_{\ell (\sigma )}$
. If
$C_{\ell (\sigma )}$
. If
![]() $\widehat {Y} \leq _{\forall \exists } \widehat {X}_{\geq m}$
, then take
$\widehat {Y} \leq _{\forall \exists } \widehat {X}_{\geq m}$
, then take
![]() $B = \widehat {X}_{\geq m}$
. Otherwise there is an n such that
$B = \widehat {X}_{\geq m}$
. Otherwise there is an n such that
![]() $y_n$
is above every element of
$y_n$
is above every element of
![]() $\widehat {X}_{\geq m}$
. In this case, take
$\widehat {X}_{\geq m}$
. In this case, take
![]() $B = \widehat {X}_{\geq m} \cup \widehat {Y}_{\geq n}$
. We show that B is
$B = \widehat {X}_{\geq m} \cup \widehat {Y}_{\geq n}$
. We show that B is
![]() $(0,\infty )$
-homogeneous.
$(0,\infty )$
-homogeneous.
Consider any
![]() $p \in P$
. If
$p \in P$
. If
![]() $p \in C_{\ell (\sigma )}$
, then p is comparable with every element of B because
$p \in C_{\ell (\sigma )}$
, then p is comparable with every element of B because
![]() $B \subseteq C_{\ell (\sigma )}$
. Suppose that
$B \subseteq C_{\ell (\sigma )}$
. Suppose that
![]() $p \in C_i$
for an
$p \in C_i$
for an
![]() $i \in \{\ell (\tau ) : \tau \text { is a child of } \sigma \text { in } T\}$
. By Claim 1, either p is above every element of X or below almost every element of Y. In either case, p is comparable with infinitely many elements of B. Finally, suppose that
$i \in \{\ell (\tau ) : \tau \text { is a child of } \sigma \text { in } T\}$
. By Claim 1, either p is above every element of X or below almost every element of Y. In either case, p is comparable with infinitely many elements of B. Finally, suppose that
![]() $p \in C_i$
for an
$p \in C_i$
for an
![]() $i \in k \setminus \bigl (\{\ell (\sigma )\} \cup \{\ell (\tau ) : \tau \text { is a child of } \sigma \text { in } T\}\bigr )$
. By Claim 2, either p is comparable with almost every element of
$i \in k \setminus \bigl (\{\ell (\sigma )\} \cup \{\ell (\tau ) : \tau \text { is a child of } \sigma \text { in } T\}\bigr )$
. By Claim 2, either p is comparable with almost every element of
![]() $X_{\geq m}$
, or p is incomparable with every element of
$X_{\geq m}$
, or p is incomparable with every element of
![]() $X_{\geq m}$
. If p is comparable with almost every element of
$X_{\geq m}$
. If p is comparable with almost every element of
![]() $X_{\geq m}$
, then p is comparable with infinitely many elements of B. Suppose instead that p is incomparable with every element of
$X_{\geq m}$
, then p is comparable with infinitely many elements of B. Suppose instead that p is incomparable with every element of
![]() $X_{\geq m}$
. If we took
$X_{\geq m}$
. If we took
![]() $B = \widehat {X}_{\geq m}$
, then p is incomparable with every element of B. Suppose that we took
$B = \widehat {X}_{\geq m}$
, then p is incomparable with every element of B. Suppose that we took
![]() $B = \widehat {X}_{\geq m} \cup \widehat {Y}_{\geq n}$
. If p is incomparable with every element of
$B = \widehat {X}_{\geq m} \cup \widehat {Y}_{\geq n}$
. If p is incomparable with every element of
![]() $\widehat {Y}_{\geq n}$
, then p is incomparable with every element of B. If p is below an element of
$\widehat {Y}_{\geq n}$
, then p is incomparable with every element of B. If p is below an element of
![]() $\widehat {Y}_{\geq n}$
, then p is below almost every element of
$\widehat {Y}_{\geq n}$
, then p is below almost every element of
![]() $\widehat {Y}_{\geq n}$
and therefore is comparable with infinity many elements of B. If p is above an element of
$\widehat {Y}_{\geq n}$
and therefore is comparable with infinity many elements of B. If p is above an element of
![]() $\widehat {Y}_{\geq n}$
, then p is above every element of
$\widehat {Y}_{\geq n}$
, then p is above every element of
![]() $\widehat {X}_{\geq m}$
and therefore is comparable with infinitely many elements of B. This completes the proof that B is
$\widehat {X}_{\geq m}$
and therefore is comparable with infinitely many elements of B. This completes the proof that B is
![]() $(0,\infty )$
-homogeneous for P.
$(0,\infty )$
-homogeneous for P.
Theorem 5.6. For each fixed standard k,
![]() $\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {RSpo}_k$
.
$\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {RSpo}_k$
.
Proof The proof is essentially the same as that of Theorem 5.5. In the proof of Theorem 5.5, the sole use of
![]() $\mathsf {I}\Sigma ^0_{2}$
is the application of bounded
$\mathsf {I}\Sigma ^0_{2}$
is the application of bounded
![]() $\Pi ^0_2$
comprehension to form the subtree
$\Pi ^0_2$
comprehension to form the subtree
![]() $T = \bigl \{\sigma \in R : \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, \sigma ) \text { is total}\bigr \}$
of the tree
$T = \bigl \{\sigma \in R : \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, \sigma ) \text { is total}\bigr \}$
of the tree
![]() $R = (k-1)^{\leq k}$
. In the case where k is fixed and standard, R and its elements have fixed standard codes, so we may instead form T by a giant case analysis, using excluded middle for the predicates
$R = (k-1)^{\leq k}$
. In the case where k is fixed and standard, R and its elements have fixed standard codes, so we may instead form T by a giant case analysis, using excluded middle for the predicates
![]() $\bigl (\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, \sigma ) \text { is total}\bigr ) \;\vee \; \bigl (\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, \sigma ) \text { is not total}\bigr )$
for the
$\bigl (\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, \sigma ) \text { is total}\bigr ) \;\vee \; \bigl (\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A, \sigma ) \text { is not total}\bigr )$
for the
![]() $\sigma \in R$
. The proof then continues exactly as in that of Theorem 5.5. The proof of Theorem 5.5 does make use of
$\sigma \in R$
. The proof then continues exactly as in that of Theorem 5.5. The proof of Theorem 5.5 does make use of
![]() $\mathsf {B}\Sigma ^0_{2}$
in addition to the aforementioned use of
$\mathsf {B}\Sigma ^0_{2}$
in addition to the aforementioned use of
![]() $\mathsf {I}\Sigma ^0_{2}$
, but the relevant instances of
$\mathsf {I}\Sigma ^0_{2}$
, but the relevant instances of
![]() $\mathsf {B}\Sigma ^0_{2}$
are provable in
$\mathsf {B}\Sigma ^0_{2}$
are provable in
![]() $\mathsf {RCA}_0$
when k is fixed and standard (plus
$\mathsf {RCA}_0$
when k is fixed and standard (plus
![]() $\mathsf {B}\Sigma ^0_{2}$
is available here anyway because
$\mathsf {B}\Sigma ^0_{2}$
is available here anyway because
![]() $\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {B}\Sigma ^0_{2}$
as explained in Section 2).
$\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {B}\Sigma ^0_{2}$
as explained in Section 2).
When working under the assumption that the partial order
![]() $(P, <_P)$
contains an infinite ascending sequence, the proof of Theorem 5.5 produces either a chain of order-type
$(P, <_P)$
contains an infinite ascending sequence, the proof of Theorem 5.5 produces either a chain of order-type
![]() $\omega $
(when taking
$\omega $
(when taking
![]() $B = \widehat {X}_{\geq m})$
or a chain of order-type
$B = \widehat {X}_{\geq m})$
or a chain of order-type
![]() $\omega + \omega $
(when taking
$\omega + \omega $
(when taking
![]() $B = \widehat {X}_{\geq m} \cup \widehat {Y}_{\geq n}$
). Therefore,
$B = \widehat {X}_{\geq m} \cup \widehat {Y}_{\geq n}$
). Therefore,
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
in fact proves that every infinite partial order of finite width contains a
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
in fact proves that every infinite partial order of finite width contains a
![]() $(0,\infty )$
-homogeneous chain of order-type
$(0,\infty )$
-homogeneous chain of order-type
![]() $\omega $
,
$\omega $
,
![]() $\omega + \omega $
,
$\omega + \omega $
,
![]() $\omega ^*$
, or
$\omega ^*$
, or
![]() $\omega ^* + \omega ^*$
. Likewise, for each fixed standard k,
$\omega ^* + \omega ^*$
. Likewise, for each fixed standard k,
![]() $\mathsf {RCA}_0 + \mathsf {ADS}$
proves that every infinite partial order of width
$\mathsf {RCA}_0 + \mathsf {ADS}$
proves that every infinite partial order of width
![]() $\leq \! k$
contains a
$\leq \! k$
contains a
![]() $(0,\infty )$
-homogeneous chain of order-type
$(0,\infty )$
-homogeneous chain of order-type
![]() $\omega $
,
$\omega $
,
![]() $\omega + \omega $
,
$\omega + \omega $
,
![]() $\omega ^*$
, or
$\omega ^*$
, or
![]() $\omega ^* + \omega ^*$
.
$\omega ^* + \omega ^*$
.
In the particular case of
![]() $\mathsf {RSpo}^{\mathsf {CD}}_2$
, we may weaken
$\mathsf {RSpo}^{\mathsf {CD}}_2$
, we may weaken
![]() $\mathsf {ADS}$
to
$\mathsf {ADS}$
to
![]() $\mathsf {SADS}$
and show that
$\mathsf {SADS}$
and show that
![]() $\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {RSpo}^{\mathsf {CD}}_2$
. To do this, we make use of a strict version of
$\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {RSpo}^{\mathsf {CD}}_2$
. To do this, we make use of a strict version of
![]() $\mathsf {SRT}^2_k$
where we assume not only that the coloring
$\mathsf {SRT}^2_k$
where we assume not only that the coloring
![]() $c \colon [\mathbb {N}]^2 \rightarrow k$
is stable, but that there is a fixed bound n such that for every x there are at most n many
$c \colon [\mathbb {N}]^2 \rightarrow k$
is stable, but that there is a fixed bound n such that for every x there are at most n many
![]() $y> x$
where
$y> x$
where
![]() $c(x, y) \neq c(x, y+1)$
.
$c(x, y) \neq c(x, y+1)$
.
Definition 5.7.
-
• A k-coloring of pairs
 $c \colon [\mathbb {N}]^2 \rightarrow k$
is n-stable if, for every x,
$c \colon [\mathbb {N}]^2 \rightarrow k$
is n-stable if, for every x,
 $|\{y> x : c(x,y) \neq c(x, y+1)\}| \leq n$
.
$|\{y> x : c(x,y) \neq c(x, y+1)\}| \leq n$
. -
•
 ${n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k}$
is the restriction of
${n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k}$
is the restriction of
 $\mathsf {RT}^2_k$
to n-stable k-colorings of pairs c.
$\mathsf {RT}^2_k$
to n-stable k-colorings of pairs c. -
•
 ${n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty }$
denotes
${n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty }$
denotes
 $\forall k \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
.
$\forall k \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
.
Proposition 5.8.
-
(1) For each fixed standard n and k,
 $\mathsf {RCA}_0 \vdash {n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k}$
.
$\mathsf {RCA}_0 \vdash {n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k}$
. -
(2) For each fixed standard n,
 $\mathsf {B}\Sigma ^0_{2}$
and
$\mathsf {B}\Sigma ^0_{2}$
and
 ${n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty }$
are equivalent over
${n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty }$
are equivalent over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
. -
(3)
 $\mathsf {I}\Sigma ^0_{2}$
and
$\mathsf {I}\Sigma ^0_{2}$
and
 $\forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty })$
are equivalent over
$\forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty })$
are equivalent over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Proof For item (1), let
![]() $c \colon [\mathbb {N}]^2 \rightarrow k$
be an n-stable k-coloring of pairs. Let
$c \colon [\mathbb {N}]^2 \rightarrow k$
be an n-stable k-coloring of pairs. Let
![]() $\varphi (x, i, c)$
be the
$\varphi (x, i, c)$
be the
![]() $\Sigma ^0_1$
formula expressing that there is a sequence
$\Sigma ^0_1$
formula expressing that there is a sequence
![]() $x < y_0 < y_1 < \dots < y_{i-1}$
of length i where
$x < y_0 < y_1 < \dots < y_{i-1}$
of length i where
![]() $\forall j < i \; (c(x, y_j) \neq c(x, y_j + 1))$
. Note that
$\forall j < i \; (c(x, y_j) \neq c(x, y_j + 1))$
. Note that
![]() $\varphi (x, 0, c)$
holds for every x. By repeated applications of excluded middle, there is a maximum
$\varphi (x, 0, c)$
holds for every x. By repeated applications of excluded middle, there is a maximum
![]() $i \leq n$
such that
$i \leq n$
such that
![]() $\varphi (x, i, c)$
holds for infinitely many x. By the maximality of i, there is a bound b such that if
$\varphi (x, i, c)$
holds for infinitely many x. By the maximality of i, there is a bound b such that if
![]() $x> b$
and
$x> b$
and
![]() $j> i$
, then
$j> i$
, then
![]() $\neg \varphi (x, j, c)$
.
$\neg \varphi (x, j, c)$
.
![]() $\mathsf {RCA}_0$
suffices to formalize the well-known fact that every infinite recursively enumerable set contains an infinite recursive subset. That is, for every
$\mathsf {RCA}_0$
suffices to formalize the well-known fact that every infinite recursively enumerable set contains an infinite recursive subset. That is, for every
![]() $\Sigma ^0_1$
formula
$\Sigma ^0_1$
formula
![]() $\psi (x)$
(possibly with parameters),
$\psi (x)$
(possibly with parameters),
![]() $\mathsf {RCA}_0$
proves that if
$\mathsf {RCA}_0$
proves that if
![]() $\psi (x)$
holds for infinitely many x, then there is an infinite set X such that
$\psi (x)$
holds for infinitely many x, then there is an infinite set X such that
![]() $\forall x \, (x \in X \rightarrow \psi (x))$
. Applying this to the
$\forall x \, (x \in X \rightarrow \psi (x))$
. Applying this to the
![]() $\Sigma ^0_1$
formula
$\Sigma ^0_1$
formula
![]() $(x> b) \wedge \varphi (x, i, c)$
, we obtain an infinite set X such that
$(x> b) \wedge \varphi (x, i, c)$
, we obtain an infinite set X such that
![]() $\forall x \, (x \in X \;\rightarrow \; (x> b) \wedge \varphi (x, i, c))$
. Then for every
$\forall x \, (x \in X \;\rightarrow \; (x> b) \wedge \varphi (x, i, c))$
. Then for every
![]() $x \in X$
, there are exactly i many elements
$x \in X$
, there are exactly i many elements
![]() $y> x$
with
$y> x$
with
![]() $c(x, y) \neq c(x, y+1)$
. So for every
$c(x, y) \neq c(x, y+1)$
. So for every
![]() $x \in X$
, there is a unique sequence
$x \in X$
, there is a unique sequence
![]() $x < y_0^x < \cdots < y_{i-1}^x$
where
$x < y_0^x < \cdots < y_{i-1}^x$
where
![]() $\forall j < i \; (c(x, y_j^x) \neq c(x, y_j^x + 1))$
. It follows that
$\forall j < i \; (c(x, y_j^x) \neq c(x, y_j^x + 1))$
. It follows that
![]() $c(x, y) = c(x, y_{i-1}^x + 1)$
for all
$c(x, y) = c(x, y_{i-1}^x + 1)$
for all
![]() $x \in X$
and
$x \in X$
and
![]() $y> y_{i-1}^x$
. Define a k-coloring of singletons
$y> y_{i-1}^x$
. Define a k-coloring of singletons
![]() $f \colon X \rightarrow k$
by
$f \colon X \rightarrow k$
by
![]() $f(x) = c(x, y_{i-1}^x + 1)$
. Apply
$f(x) = c(x, y_{i-1}^x + 1)$
. Apply
![]() $\mathsf {RT}^1_k$
to f to obtain a set
$\mathsf {RT}^1_k$
to f to obtain a set
![]() $G \subseteq X$
that is homogeneous for f for some color
$G \subseteq X$
that is homogeneous for f for some color
![]() $\ell < k$
. Now define an infinite set
$\ell < k$
. Now define an infinite set
![]() $H = \{x_s : s \in \mathbb {N}\} \subseteq G$
with
$H = \{x_s : s \in \mathbb {N}\} \subseteq G$
with
![]() $x_0 < x_1 < x_2 < \cdots $
by letting each
$x_0 < x_1 < x_2 < \cdots $
by letting each
![]() $x_s$
be the least element of G with
$x_s$
be the least element of G with
![]() $x_s \geq \max \{y_{i-1}^{x_0}, y_{i-1}^{x_1}, \dots , y_{i-1}^{x_{s-1}}\} + 1$
. Then H is homogeneous for c. If
$x_s \geq \max \{y_{i-1}^{x_0}, y_{i-1}^{x_1}, \dots , y_{i-1}^{x_{s-1}}\} + 1$
. Then H is homogeneous for c. If
![]() $s < t$
, then
$s < t$
, then
![]() $x_t \geq y_{i-1}^{x_s} + 1$
, so
$x_t \geq y_{i-1}^{x_s} + 1$
, so
![]() $c(x_s, x_t) = c(x_s, y_{i-1}^{x_s} + 1) = f(x_s) = \ell $
.
$c(x_s, x_t) = c(x_s, y_{i-1}^{x_s} + 1) = f(x_s) = \ell $
.
For the forward direction of item (2), we may use the same proof as for item (1), except now k is arbitrary so we must use
![]() $\mathsf {RT}^1_{<\infty }$
in place of
$\mathsf {RT}^1_{<\infty }$
in place of
![]() $\mathsf {RT}^1_k$
. For the reversal, it is easy to see that
$\mathsf {RT}^1_k$
. For the reversal, it is easy to see that
![]() $\mathsf {RCA}_0 + {0}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty } \vdash \mathsf {RT}^1_{<\infty }$
. Let
$\mathsf {RCA}_0 + {0}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty } \vdash \mathsf {RT}^1_{<\infty }$
. Let
![]() $f \colon \mathbb {N} \rightarrow k$
be a k-coloring of singletons for some k, and define
$f \colon \mathbb {N} \rightarrow k$
be a k-coloring of singletons for some k, and define
![]() $c \colon [\mathbb {N}]^2 \rightarrow k$
by
$c \colon [\mathbb {N}]^2 \rightarrow k$
by
![]() $c(x,y) = f(x)$
. Then c is a
$c(x,y) = f(x)$
. Then c is a
![]() $0$
-stable k-coloring of pairs, and every H that is homogeneous for c is also homogeneous for f.
$0$
-stable k-coloring of pairs, and every H that is homogeneous for c is also homogeneous for f.
For the forward direction of item (3), we may use the same proof as for item (2), except now n is also arbitrary, so we must use
![]() $\mathsf {I}\Sigma ^0_{2}$
in the form of the
$\mathsf {I}\Sigma ^0_{2}$
in the form of the
![]() $\Pi ^0_2$
least element principle (see Section 2) to obtain i. To do this, apply the
$\Pi ^0_2$
least element principle (see Section 2) to obtain i. To do this, apply the
![]() $\Pi ^0_2$
least element principle to obtain the least j such that
$\Pi ^0_2$
least element principle to obtain the least j such that
![]() $\forall s \; \exists x> s \; \varphi (x, n-j, c)$
. Then
$\forall s \; \exists x> s \; \varphi (x, n-j, c)$
. Then
![]() $i = n-j$
is the greatest
$i = n-j$
is the greatest
![]() $i \leq n$
such that
$i \leq n$
such that
![]() $\varphi (x, i, c)$
holds for infinitely many x. For the reversal, we show that
$\varphi (x, i, c)$
holds for infinitely many x. For the reversal, we show that
![]() $\mathsf {RCA}_0 + \forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty })$
proves the
$\mathsf {RCA}_0 + \forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty })$
proves the
![]() $\Pi ^0_2$
least element principle. Let
$\Pi ^0_2$
least element principle. Let
![]() $\forall x \, \exists y \, \psi (m, x, y)$
be a
$\forall x \, \exists y \, \psi (m, x, y)$
be a
![]() $\Pi ^0_2$
formula, possibly with undisplayed parameters, where
$\Pi ^0_2$
formula, possibly with undisplayed parameters, where
![]() $\psi $
is
$\psi $
is
![]() $\Sigma ^0_0$
. Let k be such that
$\Sigma ^0_0$
. Let k be such that
![]() $\forall x \, \exists y \, \psi (k, x, y)$
. We want to find the least i such that
$\forall x \, \exists y \, \psi (k, x, y)$
. We want to find the least i such that
![]() $\forall x \, \exists y \, \psi (i, x, y)$
. Define a
$\forall x \, \exists y \, \psi (i, x, y)$
. Define a
![]() $(k+2)$
-coloring of pairs
$(k+2)$
-coloring of pairs
![]() $c \colon [\mathbb {N}]^2 \rightarrow k+2$
by
$c \colon [\mathbb {N}]^2 \rightarrow k+2$
by
 $$ \begin{align*} c(s,t) = \begin{cases} i, & \text{if } i \leq k \text{ is least such that } \forall x \leq s \; \exists y \leq t \; \psi(i, x, y),\\ k+1, & \text{if } \forall i \leq k \; \exists x \leq s \; \forall y \leq t \; \neg\psi(i, x, y). \end{cases} \end{align*} $$
$$ \begin{align*} c(s,t) = \begin{cases} i, & \text{if } i \leq k \text{ is least such that } \forall x \leq s \; \exists y \leq t \; \psi(i, x, y),\\ k+1, & \text{if } \forall i \leq k \; \exists x \leq s \; \forall y \leq t \; \neg\psi(i, x, y). \end{cases} \end{align*} $$
The coloring c is
![]() $(k+2)$
-stable because, for fixed s, if
$(k+2)$
-stable because, for fixed s, if
![]() $s < t_0 < t_1$
, then
$s < t_0 < t_1$
, then
![]() $c(s, t_0) \geq c(s, t_1)$
. By
$c(s, t_0) \geq c(s, t_1)$
. By
![]() $\forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty })$
, let H be a set that is homogeneous for c with color i. Then i is least such that
$\forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{<\infty })$
, let H be a set that is homogeneous for c with color i. Then i is least such that
![]() $\forall x \, \exists y \, \psi (i, x, y)$
. To see this, we first show that if
$\forall x \, \exists y \, \psi (i, x, y)$
. To see this, we first show that if
![]() $j \leq k$
and
$j \leq k$
and
![]() $\forall x \, \exists y \, \psi (j, x, y)$
, then
$\forall x \, \exists y \, \psi (j, x, y)$
, then
![]() $i \leq j$
. Let
$i \leq j$
. Let
![]() $s \in H$
, and, by
$s \in H$
, and, by
![]() $\mathsf {B}\Sigma ^0_{0}$
and the assumption
$\mathsf {B}\Sigma ^0_{0}$
and the assumption
![]() $\forall x \, \exists y \, \psi (j, x, y)$
, let
$\forall x \, \exists y \, \psi (j, x, y)$
, let
![]() $t \in H$
be large enough so that
$t \in H$
be large enough so that
![]() $t> s$
and
$t> s$
and
![]() $\forall x \leq s \; \exists y \leq t \; \psi (j, x, y)$
. Then
$\forall x \leq s \; \exists y \leq t \; \psi (j, x, y)$
. Then
![]() $i = c(s,t) \leq j$
, so
$i = c(s,t) \leq j$
, so
![]() $i \leq j$
. It follows that
$i \leq j$
. It follows that
![]() $i \leq k$
by the assumption
$i \leq k$
by the assumption
![]() $\forall x \, \exists y \, \psi (k, x, y)$
. Now we show that
$\forall x \, \exists y \, \psi (k, x, y)$
. Now we show that
![]() $\forall x \, \exists y \, \psi (i, x, y)$
. Consider any
$\forall x \, \exists y \, \psi (i, x, y)$
. Consider any
![]() $x_0$
, and let
$x_0$
, and let
![]() $s, t \in H$
be such that
$s, t \in H$
be such that
![]() $x_0 < s < t$
. Then
$x_0 < s < t$
. Then
![]() $c(s,t) = i$
and
$c(s,t) = i$
and
![]() $i \leq k$
, so i is least such that
$i \leq k$
, so i is least such that
![]() $\forall x \leq s \; \exists y \leq t \; \psi (i, x, y)$
. In particular,
$\forall x \leq s \; \exists y \leq t \; \psi (i, x, y)$
. In particular,
![]() $\exists y \, \psi (i, x_0, y)$
because
$\exists y \, \psi (i, x_0, y)$
because
![]() $x_0 < s$
. Therefore
$x_0 < s$
. Therefore
![]() $\forall x \, \exists y \, \psi (i, x, y)$
. Thus i is least such that
$\forall x \, \exists y \, \psi (i, x, y)$
. Thus i is least such that
![]() $\forall x \, \exists y \, \psi (i, x, y)$
.
$\forall x \, \exists y \, \psi (i, x, y)$
.
Our proof of
![]() $\mathsf {RSpo}^{\mathsf {CD}}_2$
in
$\mathsf {RSpo}^{\mathsf {CD}}_2$
in
![]() $\mathsf {RCA}_0 + \mathsf {SADS}$
only uses the principle
$\mathsf {RCA}_0 + \mathsf {SADS}$
only uses the principle
![]() ${2}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{3}$
from Proposition 5.8 item (1). We include items (2) and (3) for completeness. For fixed standard
${2}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{3}$
from Proposition 5.8 item (1). We include items (2) and (3) for completeness. For fixed standard
![]() $k \geq 2$
, one might also consider the principle
$k \geq 2$
, one might also consider the principle
![]() $\forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
. That
$\forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
. That
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} \vdash \forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
follows from Proposition 5.8 item (3), but there cannot be a reversal because
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} \vdash \forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
follows from Proposition 5.8 item (3), but there cannot be a reversal because
![]() $\mathsf {RCA}_0 + \mathsf {SRT}^2_k \vdash \forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
, but
$\mathsf {RCA}_0 + \mathsf {SRT}^2_k \vdash \forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
, but
![]() $\mathsf {RCA}_0 + \mathsf {SRT}^2_k \nvdash \mathsf {I}\Sigma ^0_{2}$
(see Section 2). We did not determine if
$\mathsf {RCA}_0 + \mathsf {SRT}^2_k \nvdash \mathsf {I}\Sigma ^0_{2}$
(see Section 2). We did not determine if
![]() $\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_{2} \vdash \forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
.
$\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_{2} \vdash \forall n \, ({n}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{k})$
.
Theorem 5.9.
![]() $\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {RSpo}^{\mathsf {CD}}_2$
.
$\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {RSpo}^{\mathsf {CD}}_2$
.
Proof By inspecting the proofs of Theorems 5.5 and 5.6, we see that the only use of
![]() $\mathsf {ADS}$
is to produce either an infinite ascending sequence or an infinite descending sequence in the partial order. That is,
$\mathsf {ADS}$
is to produce either an infinite ascending sequence or an infinite descending sequence in the partial order. That is,
![]() $\mathsf {RCA}_0$
proves the following for each fixed standard k.
$\mathsf {RCA}_0$
proves the following for each fixed standard k.
-
(⋆) Let
 $(P, <_P)$
be an infinite k-chain decomposable partial order that contains either an infinite ascending sequence or an infinite descending sequence. Then P contains a
$(P, <_P)$
be an infinite k-chain decomposable partial order that contains either an infinite ascending sequence or an infinite descending sequence. Then P contains a
 $(0,\infty )$
-homogeneous chain.
$(0,\infty )$
-homogeneous chain.
Let
![]() $(P, <_P)$
be an infinite partial order with
$(P, <_P)$
be an infinite partial order with
![]() $2$
-chain decomposition
$2$
-chain decomposition
![]() $C_0, C_1$
. The plan of the proof is to either produce a
$C_0, C_1$
. The plan of the proof is to either produce a
![]() $(0,\infty )$
-homogeneous chain outright or to apply
$(0,\infty )$
-homogeneous chain outright or to apply
![]() $\mathsf {SADS}$
to obtain an infinite ascending sequence or an infinite descending sequence in P, in which case we may produce a
$\mathsf {SADS}$
to obtain an infinite ascending sequence or an infinite descending sequence in P, in which case we may produce a
![]() $(0,\infty )$
-homogeneous chain in P by applying
$(0,\infty )$
-homogeneous chain in P by applying
![]() $(\star )$
. Notice that we may make free use of
$(\star )$
. Notice that we may make free use of
![]() $\mathsf {B}\Sigma ^0_{2}$
because
$\mathsf {B}\Sigma ^0_{2}$
because
![]() $\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {B}\Sigma ^0_{2}$
as explained in Section 2.
$\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {B}\Sigma ^0_{2}$
as explained in Section 2.
The partial order P is infinite, so at least one of
![]() $C_0$
and
$C_0$
and
![]() $C_1$
is infinite. Assume that
$C_1$
is infinite. Assume that
![]() $C_0$
is infinite for the sake of argument.
$C_0$
is infinite for the sake of argument.
Claim 1. Suppose that there are an infinite
![]() $D_0 \subseteq C_0$
and a finite
$D_0 \subseteq C_0$
and a finite
![]() $D_1 \subseteq C_1$
such that
$D_1 \subseteq C_1$
such that
![]() $D_0 \mid _P (C_1 \setminus D_1)$
. Then P contains a
$D_0 \mid _P (C_1 \setminus D_1)$
. Then P contains a
![]() $(0,\infty )$
-homogeneous chain.
$(0,\infty )$
-homogeneous chain.
Proof of Claim
Suppose that
![]() $D_1 = \{q_0, \dots , q_{n-1}\}$
, and define a
$D_1 = \{q_0, \dots , q_{n-1}\}$
, and define a
![]() $2^n$
-coloring
$2^n$
-coloring
![]() $f \colon D_0 \rightarrow 2^n$
by
$f \colon D_0 \rightarrow 2^n$
by
![]() $f(p) = \langle b_0, \dots , b_{n-1}\rangle $
, where, for each
$f(p) = \langle b_0, \dots , b_{n-1}\rangle $
, where, for each
![]() $i < n$
,
$i < n$
,
![]() $b_i = 0$
if
$b_i = 0$
if
![]() $p \mid _P q_i$
and
$p \mid _P q_i$
and
![]() $b_i = 1$
if
$b_i = 1$
if
![]() $p \lessgtr _P q_i$
. Apply
$p \lessgtr _P q_i$
. Apply
![]() $\mathsf {RT}^1_{<\infty }$
to f to obtain an infinite set
$\mathsf {RT}^1_{<\infty }$
to f to obtain an infinite set
![]() $H \subseteq D_0$
that is homogeneous for f. Then H is a
$H \subseteq D_0$
that is homogeneous for f. Then H is a
![]() $(0,\infty )$
-homogeneous chain for P. H is a chain because
$(0,\infty )$
-homogeneous chain for P. H is a chain because
![]() $H \subseteq D_0 \subseteq C_0$
and
$H \subseteq D_0 \subseteq C_0$
and
![]() $C_0$
is a chain. Consider a
$C_0$
is a chain. Consider a
![]() $q \in P$
. If
$q \in P$
. If
![]() $q \in C_0$
, then q is comparable with every element of H because
$q \in C_0$
, then q is comparable with every element of H because
![]() $H \subseteq C_0$
and
$H \subseteq C_0$
and
![]() $C_0$
is a chain. If
$C_0$
is a chain. If
![]() $q \in C_1 \setminus D_1$
, then q is incomparable with every element of
$q \in C_1 \setminus D_1$
, then q is incomparable with every element of
![]() $D_0$
by assumption and therefore is incomparable with every element of H because
$D_0$
by assumption and therefore is incomparable with every element of H because
![]() $H \subseteq D_0$
. If
$H \subseteq D_0$
. If
![]() $q \in D_1$
, then
$q \in D_1$
, then
![]() $q = q_i$
for some
$q = q_i$
for some
![]() $i < n$
, so by the homogeneity of H, either q is comparable with every element of H or q is incomparable with every element of H.
$i < n$
, so by the homogeneity of H, either q is comparable with every element of H or q is incomparable with every element of H.
If
![]() $C_1$
is finite, then we may apply Claim 1 with
$C_1$
is finite, then we may apply Claim 1 with
![]() $D_0 = C_0$
and
$D_0 = C_0$
and
![]() $D_1 = C_1$
to obtain a
$D_1 = C_1$
to obtain a
![]() $(0,\infty )$
-homogeneous chain for P. Thus we may assume that
$(0,\infty )$
-homogeneous chain for P. Thus we may assume that
![]() $C_0$
and
$C_0$
and
![]() $C_1$
are both infinite. Let
$C_1$
are both infinite. Let
![]() $\langle p_n : n \in \mathbb {N} \rangle $
be a bijective enumeration of
$\langle p_n : n \in \mathbb {N} \rangle $
be a bijective enumeration of
![]() $C_0$
, and let
$C_0$
, and let
![]() $\langle q_n : n \in \mathbb {N} \rangle $
be a bijective enumeration of
$\langle q_n : n \in \mathbb {N} \rangle $
be a bijective enumeration of
![]() $C_1$
. The goal is now to work into a situation where the following claim applies.
$C_1$
. The goal is now to work into a situation where the following claim applies.
Claim 2. Suppose that there is an infinite
![]() $H \subseteq \mathbb {N}$
and an injection
$H \subseteq \mathbb {N}$
and an injection
![]() $f \colon H \rightarrow \mathbb {N}$
where
$f \colon H \rightarrow \mathbb {N}$
where
![]() $\forall n \in H \; \bigl (p_n \lessgtr _P q_{f(n)}\bigr )$
. Then P contains a
$\forall n \in H \; \bigl (p_n \lessgtr _P q_{f(n)}\bigr )$
. Then P contains a
![]() $(0,\infty )$
-homogeneous chain.
$(0,\infty )$
-homogeneous chain.
Proof of Claim
We may assume that the range of f exists as a set by shrinking H if necessary.
For this argument, for a
![]() $p \in C_0$
, let
$p \in C_0$
, let
![]() $p{\uparrow } = \{x \in C_0 : x \geq _P p\}$
and
$p{\uparrow } = \{x \in C_0 : x \geq _P p\}$
and
![]() $p{\downarrow } = \{x \in C_0 : x \leq _P p\}$
denote the upward and downward closures of p in
$p{\downarrow } = \{x \in C_0 : x \leq _P p\}$
denote the upward and downward closures of p in
![]() $C_0$
. Similarly, for a
$C_0$
. Similarly, for a
![]() $q \in C_1$
, let
$q \in C_1$
, let
![]() $q{\uparrow }$
and
$q{\uparrow }$
and
![]() $q{\downarrow }$
denote the upward and downward closures of q in
$q{\downarrow }$
denote the upward and downward closures of q in
![]() $C_1$
.
$C_1$
.
Let
![]() $X = \{n \in H : p_n <_P q_{f(n)}\}$
, and let
$X = \{n \in H : p_n <_P q_{f(n)}\}$
, and let
![]() $Y = \{n \in H : p_n>_P q_{f(n)}\}$
. Then
$Y = \{n \in H : p_n>_P q_{f(n)}\}$
. Then
![]() ${H = X \cup Y}$
, so at least one of X and Y is infinite. The two cases are symmetric, so suppose that X is infinite for the sake of argument. Let
${H = X \cup Y}$
, so at least one of X and Y is infinite. The two cases are symmetric, so suppose that X is infinite for the sake of argument. Let
![]() $L = \{p_n : n \in X\}$
. Then
$L = \{p_n : n \in X\}$
. Then
![]() $L \subseteq C_0$
and
$L \subseteq C_0$
and
![]() $C_0$
is a chain, so L is an infinite linear order. If L is also stable, then it has either an infinite ascending sequence or an infinite descending sequence by
$C_0$
is a chain, so L is an infinite linear order. If L is also stable, then it has either an infinite ascending sequence or an infinite descending sequence by
![]() $\mathsf {SADS}$
. Thus P has either an infinite ascending sequence or an infinite descending sequence, so P has a
$\mathsf {SADS}$
. Thus P has either an infinite ascending sequence or an infinite descending sequence, so P has a
![]() $(0,\infty )$
-homogeneous chain by
$(0,\infty )$
-homogeneous chain by
![]() $(\star )$
.
$(\star )$
.
If L is not stable, then let
![]() $n \in X$
be such that
$n \in X$
be such that
![]() $p_n{\uparrow } \cap L$
and
$p_n{\uparrow } \cap L$
and
![]() $p_n{\downarrow } \cap L$
are both infinite. Suppose that there is an
$p_n{\downarrow } \cap L$
are both infinite. Suppose that there is an
![]() $m \in X$
where
$m \in X$
where
![]() $p_n \leq _P p_m$
and
$p_n \leq _P p_m$
and
![]() $q_{f(m)}{\uparrow }$
is infinite. Then
$q_{f(m)}{\uparrow }$
is infinite. Then
![]() $p_n \leq _P p_m <_P q_{f(m)}$
, so
$p_n \leq _P p_m <_P q_{f(m)}$
, so
![]() $C = p_n {\downarrow } \cup q_{f(m)}{\uparrow }$
is an infinite chain in P. Furthermore, C is
$C = p_n {\downarrow } \cup q_{f(m)}{\uparrow }$
is an infinite chain in P. Furthermore, C is
![]() $(0,\infty )$
-homogeneous because it has infinite intersection with both
$(0,\infty )$
-homogeneous because it has infinite intersection with both
![]() $C_0$
and
$C_0$
and
![]() $C_1$
. Finally, suppose instead that
$C_1$
. Finally, suppose instead that
![]() $q_{f(m)}{\uparrow }$
is finite whenever
$q_{f(m)}{\uparrow }$
is finite whenever
![]() $m \in X$
and
$m \in X$
and
![]() $p_n \leq _P p_m$
. Then the set
$p_n \leq _P p_m$
. Then the set
![]() $\{q_{f(m)} : m \in X \;\wedge \; p_m \geq _P p_n\} \subseteq C_1$
is an infinite chain because
$\{q_{f(m)} : m \in X \;\wedge \; p_m \geq _P p_n\} \subseteq C_1$
is an infinite chain because
![]() $p_n {\uparrow } \cap L$
is infinite, but it has no least element. We may therefore define an infinite descending sequence in
$p_n {\uparrow } \cap L$
is infinite, but it has no least element. We may therefore define an infinite descending sequence in
![]() $\{q_{f(m)} : m \in X \;\wedge \; p_m \geq _P p_n\}$
. Thus P has an infinite descending sequence, so it has a
$\{q_{f(m)} : m \in X \;\wedge \; p_m \geq _P p_n\}$
. Thus P has an infinite descending sequence, so it has a
![]() $(0,\infty )$
-homogeneous chain by
$(0,\infty )$
-homogeneous chain by
![]() $(\star )$
.
$(\star )$
.
To finish the proof, define a coloring
![]() $c \colon [\mathbb {N}]^2 \rightarrow 3$
as follows:
$c \colon [\mathbb {N}]^2 \rightarrow 3$
as follows:
 $$ \begin{align*} c(n,m) = \begin{cases} 0, & \text{if } \forall i \leq m \; (p_n \mid_P q_i),\\ 1, & \text{if } \exists i \, (n < i \leq m \;\wedge\; p_n \lessgtr_P q_i),\\ 2, & \text{if } \exists i \, (i \leq n \;\wedge\; p_n \lessgtr_P q_i) \;\wedge\; \forall i \, (n < i \leq m \;\rightarrow\; p_n \mid_P q_i). \end{cases} \end{align*} $$
$$ \begin{align*} c(n,m) = \begin{cases} 0, & \text{if } \forall i \leq m \; (p_n \mid_P q_i),\\ 1, & \text{if } \exists i \, (n < i \leq m \;\wedge\; p_n \lessgtr_P q_i),\\ 2, & \text{if } \exists i \, (i \leq n \;\wedge\; p_n \lessgtr_P q_i) \;\wedge\; \forall i \, (n < i \leq m \;\rightarrow\; p_n \mid_P q_i). \end{cases} \end{align*} $$
For every n, the color of
![]() $c(n,m)$
changes at most twice. This can be seen by considering the value of
$c(n,m)$
changes at most twice. This can be seen by considering the value of
![]() $c(n, n+1)$
and making the following observations:
$c(n, n+1)$
and making the following observations:
-
• If
 $c(n, m_0) = 0$
for some
$c(n, m_0) = 0$
for some
 $m_0> n$
, then
$m_0> n$
, then
 $c(n,m) \neq 2$
for all
$c(n,m) \neq 2$
for all
 $m \geq m_0$
.
$m \geq m_0$
. -
• If
 $c(n, m_0) = 1$
for some
$c(n, m_0) = 1$
for some
 $m_0> n$
, then
$m_0> n$
, then
 $c(n,m) = 1$
for all
$c(n,m) = 1$
for all
 $m \geq m_0$
.
$m \geq m_0$
. -
• If
 $c(n, m_0) = 2$
for some
$c(n, m_0) = 2$
for some
 $m_0> n$
, then
$m_0> n$
, then
 $c(n,m) \neq 0$
for all
$c(n,m) \neq 0$
for all
 $m \geq m_0$
.
$m \geq m_0$
.
Apply
![]() ${2}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{3}$
, which is provable in
${2}\text {-}\mathrm {stable~}\mathsf {SRT}^{2}_{3}$
, which is provable in
![]() $\mathsf {RCA}_0$
by Proposition 5.8 item (1), to c to obtain a set H that is homogeneous for c, and consider the color for which H is homogeneous.
$\mathsf {RCA}_0$
by Proposition 5.8 item (1), to c to obtain a set H that is homogeneous for c, and consider the color for which H is homogeneous.
Suppose that H is
![]() $0$
-homogeneous. Let
$0$
-homogeneous. Let
![]() $C = \{p_n : n \in H\}$
. Then
$C = \{p_n : n \in H\}$
. Then
![]() $C \subseteq C_0$
is an infinite chain, and thus every element of
$C \subseteq C_0$
is an infinite chain, and thus every element of
![]() $C_0$
is comparable with every element of C. Furthermore, every element of
$C_0$
is comparable with every element of C. Furthermore, every element of
![]() $C_1$
is incomparable with every element of C because H is
$C_1$
is incomparable with every element of C because H is
![]() $0$
-homogeneous. So C is a
$0$
-homogeneous. So C is a
![]() $(0,\infty )$
-homogeneous chain for P.
$(0,\infty )$
-homogeneous chain for P.
Suppose that H is
![]() $1$
-homogeneous. Define a function
$1$
-homogeneous. Define a function
![]() $f \colon H \rightarrow \mathbb {N}$
by
$f \colon H \rightarrow \mathbb {N}$
by
![]() $f(n) = i$
, where i is
$f(n) = i$
, where i is
![]() $<$
-least with
$<$
-least with
![]() $i> n$
and
$i> n$
and
![]() $p_n \lessgtr _P q_i$
. Such an i exists by the
$p_n \lessgtr _P q_i$
. Such an i exists by the
![]() $1$
-homogeneity of H. The function f is injective because if n and m are members of H with
$1$
-homogeneity of H. The function f is injective because if n and m are members of H with
![]() $n < m$
, then
$n < m$
, then
![]() $f(n) \leq m$
and
$f(n) \leq m$
and
![]() $f(m)> m$
. Thus H and f satisfy the hypothesis of Claim 2, so P contains a
$f(m)> m$
. Thus H and f satisfy the hypothesis of Claim 2, so P contains a
![]() $(0,\infty )$
-homogeneous chain.
$(0,\infty )$
-homogeneous chain.
Finally, suppose that H is
![]() $2$
-homogeneous. First, suppose that there is a bound
$2$
-homogeneous. First, suppose that there is a bound
![]() $m_0$
such that
$m_0$
such that
![]() $\forall n \in H \; \forall i \geq m_0 \; (p_n \mid _P q_i)$
. In this case,
$\forall n \in H \; \forall i \geq m_0 \; (p_n \mid _P q_i)$
. In this case,
![]() $D_0 = \{p_n : n \in H\}$
and
$D_0 = \{p_n : n \in H\}$
and
![]() $D_1 = \{q_0, \dots , q_{m_0 - 1}\}$
satisfy the hypothesis of Claim 1, so P contains a
$D_1 = \{q_0, \dots , q_{m_0 - 1}\}$
satisfy the hypothesis of Claim 1, so P contains a
![]() $(0,\infty )$
-homogeneous chain. If there is no such bound
$(0,\infty )$
-homogeneous chain. If there is no such bound
![]() $m_0$
, then
$m_0$
, then
![]() $\forall m_0 \; \exists n \in H \; \exists i \geq m_0 \; (p_n \lessgtr _P q_i)$
. However, given
$\forall m_0 \; \exists n \in H \; \exists i \geq m_0 \; (p_n \lessgtr _P q_i)$
. However, given
![]() $m_0$
, there cannot be a witnessing
$m_0$
, there cannot be a witnessing
![]() $n \in H$
and
$n \in H$
and
![]() $i \geq m_0$
with
$i \geq m_0$
with
![]() $n < m_0$
. If there were, then we could choose an
$n < m_0$
. If there were, then we could choose an
![]() $m \in H$
with
$m \in H$
with
![]() $m> i$
, in which case we would have
$m> i$
, in which case we would have
![]() $n, m \in H$
,
$n, m \in H$
,
![]() $n < i < m$
, and
$n < i < m$
, and
![]() $p_n \lessgtr _P q_i$
. We would then have that
$p_n \lessgtr _P q_i$
. We would then have that
![]() $c(n,m) = 1$
, which contradicts that H is
$c(n,m) = 1$
, which contradicts that H is
![]() $2$
-homogeneous. Therefore, the situation is that
$2$
-homogeneous. Therefore, the situation is that
![]() $\forall m \, \exists n \geq m \, \exists i \geq m \, (n \in H \;\wedge \; p_n \lessgtr _P q_i)$
. We can thus define an infinite subset
$\forall m \, \exists n \geq m \, \exists i \geq m \, (n \in H \;\wedge \; p_n \lessgtr _P q_i)$
. We can thus define an infinite subset
![]() $H_0 = \{n_0, n_1, n_2, \dots \}$
of H and an injection
$H_0 = \{n_0, n_1, n_2, \dots \}$
of H and an injection
![]() $f \colon H_0 \rightarrow \mathbb {N}$
as follows. Given
$f \colon H_0 \rightarrow \mathbb {N}$
as follows. Given
![]() $n_0 < n_1 < \cdots < n_{\ell -1}$
and
$n_0 < n_1 < \cdots < n_{\ell -1}$
and
![]() $f(n_0), f(n_1), \dots , f(n_{\ell -1})$
, search for the first pair
$f(n_0), f(n_1), \dots , f(n_{\ell -1})$
, search for the first pair
![]() $\langle n, i \rangle $
with n and i both greater than
$\langle n, i \rangle $
with n and i both greater than
![]() $\max _<\{n_0, \dots , n_{\ell -1}, f(n_0), \dots , f(n_{\ell -1})\}$
, with
$\max _<\{n_0, \dots , n_{\ell -1}, f(n_0), \dots , f(n_{\ell -1})\}$
, with
![]() $n \in H$
, and with
$n \in H$
, and with
![]() $p_n \lessgtr _P q_i$
; put
$p_n \lessgtr _P q_i$
; put
![]() $n_{\ell } = n$
; and put
$n_{\ell } = n$
; and put
![]() $f(n_{\ell }) = i$
. Then
$f(n_{\ell }) = i$
. Then
![]() $H_0$
and f satisfy the hypothesis of Claim 2, so P contains a
$H_0$
and f satisfy the hypothesis of Claim 2, so P contains a
![]() $(0,\infty )$
-homogeneous chain.
$(0,\infty )$
-homogeneous chain.
Finally, we show that
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
is provable in
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
is provable in
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
. To do this, we first adapt Lemma 5.3 for use with partial orders of width
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
. To do this, we first adapt Lemma 5.3 for use with partial orders of width
![]() $\leq \! 2$
.
$\leq \! 2$
.
Lemma 5.10. The following is provable in
![]() $\mathsf {RCA}_0$
. Let
$\mathsf {RCA}_0$
. Let
![]() $(P, <_P)$
be a partial order of width
$(P, <_P)$
be a partial order of width
![]() $\leq \! 2$
, and let
$\leq \! 2$
, and let
![]() $\vec {P}$
denote
$\vec {P}$
denote
![]() $\vec {P} = P \oplus {<_P}$
. Then there is a Turing functional
$\vec {P} = P \oplus {<_P}$
. Then there is a Turing functional
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \rightarrow P^{\mathbb {N}}$
relative to
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \rightarrow P^{\mathbb {N}}$
relative to
![]() $\vec {P}$
with the following properties for every infinite sequence
$\vec {P}$
with the following properties for every infinite sequence
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
in P.
$A = \langle a_n : n \in \mathbb {N} \rangle $
in P.
-
(1) If A is an infinite ascending sequence in P and
 $$ \begin{align*} \forall m \; \exists n> m \; \exists p \in P \; \bigl(p \geq_P a_m \;\wedge\; p \mid_P a_n\bigr), \end{align*} $$
$$ \begin{align*} \forall m \; \exists n> m \; \exists p \in P \; \bigl(p \geq_P a_m \;\wedge\; p \mid_P a_n\bigr), \end{align*} $$
then
 $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)$
is total.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)$
is total. -
(2) If
 $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)$
is total, then it computes a ladder for A in P such that
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)$
is total, then it computes a ladder for A in P such that  $$ \begin{align*} \forall m \; \exists n> m \; \bigl(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(A)(m) \mid_P a_n\bigr). \end{align*} $$
$$ \begin{align*} \forall m \; \exists n> m \; \bigl(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(A)(m) \mid_P a_n\bigr). \end{align*} $$
Proof Let
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite sequence in P. Compute
$A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite sequence in P. Compute
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(0)$
by searching for an
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(0)$
by searching for an
![]() $n> 0$
and a
$n> 0$
and a
![]() $p_0 \in P$
with
$p_0 \in P$
with
![]() $p_0 \geq _P a_0$
and
$p_0 \geq _P a_0$
and
![]() $p_0 \mid _P a_n$
. If
$p_0 \mid _P a_n$
. If
![]() $p_0$
is found, then output
$p_0$
is found, then output
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(0) = p_0$
. To compute
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(0) = p_0$
. To compute
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1)$
, first compute
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1)$
, first compute
![]() $p_m = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m)$
. Then search for an
$p_m = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m)$
. Then search for an
![]() $n> m+1$
and a
$n> m+1$
and a
![]() $p_{m+1} \in P$
with
$p_{m+1} \in P$
with
![]() $p_{m+1}>_P p_m$
,
$p_{m+1}>_P p_m$
,
![]() $p_{m+1} \geq _P a_{m+1}$
, and
$p_{m+1} \geq _P a_{m+1}$
, and
![]() $p_{m+1} \mid _P a_n$
. If
$p_{m+1} \mid _P a_n$
. If
![]() $p_{m+1}$
is found, then output
$p_{m+1}$
is found, then output
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1) = p_{m+1}$
.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1) = p_{m+1}$
.
Item (2) follows immediately from the definition of
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}$
. If
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}$
. If
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
is an infinite sequence in P and if
$A = \langle a_n : n \in \mathbb {N} \rangle $
is an infinite sequence in P and if
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)$
is total, then for every m it must be that
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)$
is total, then for every m it must be that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m) \in P$
, that
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m) \in P$
, that
![]() $a_m \leq _P \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m)$
, that
$a_m \leq _P \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m)$
, that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m) <_P \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1)$
, and that there is an
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m) <_P \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1)$
, and that there is an
![]() $n> m$
such that
$n> m$
such that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m) \mid _P a_n$
.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m) \mid _P a_n$
.
For item (1), let
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in P, and suppose that for every m there are an
$A = \langle a_n : n \in \mathbb {N} \rangle $
be an infinite ascending sequence in P, and suppose that for every m there are an
![]() $n> m$
and a
$n> m$
and a
![]() $p \in P$
with
$p \in P$
with
![]() $p \geq _P a_m$
and
$p \geq _P a_m$
and
![]() $p \mid _P a_n$
. We use
$p \mid _P a_n$
. We use
![]() $\mathsf {I}\Sigma ^0_{1}$
to show that
$\mathsf {I}\Sigma ^0_{1}$
to show that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)$
is total. By assumption, there are an
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)$
is total. By assumption, there are an
![]() $n> 0$
and a
$n> 0$
and a
![]() $p_0 \in P$
with
$p_0 \in P$
with
![]() $p_0 \geq _P a_0$
and
$p_0 \geq _P a_0$
and
![]() $p_0 \mid _P a_n$
. Thus
$p_0 \mid _P a_n$
. Thus
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(0)$
is defined. Inductively assume that
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(0)$
is defined. Inductively assume that
![]() $p_m = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m)$
is defined. Then
$p_m = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m)$
is defined. Then
![]() $p_m \geq _P a_m$
, and there is an
$p_m \geq _P a_m$
, and there is an
![]() $\ell> m$
such that
$\ell> m$
such that
![]() $p_m \mid _P a_{\ell }$
. By assumption, there are an
$p_m \mid _P a_{\ell }$
. By assumption, there are an
![]() $s> \ell $
and an
$s> \ell $
and an
![]() $x \in P$
with
$x \in P$
with
Notice that
![]() $a_{m+1} \leq _P a_{\ell } \leq _P a_s$
because
$a_{m+1} \leq _P a_{\ell } \leq _P a_s$
because
![]() $m+1 \leq \ell \leq s$
and A is an ascending sequence. The element
$m+1 \leq \ell \leq s$
and A is an ascending sequence. The element
![]() $p_m$
is comparable either with x or with
$p_m$
is comparable either with x or with
![]() $a_s$
because
$a_s$
because
![]() $x \mid _P a_s$
and P has width
$x \mid _P a_s$
and P has width
![]() $\leq \! 2$
. Also,
$\leq \! 2$
. Also,
![]() $x \nleq _P p_m$
because otherwise we would have the contradiction
$x \nleq _P p_m$
because otherwise we would have the contradiction
![]() $a_{\ell } \leq _P x \leq _P p_m$
. Similarly,
$a_{\ell } \leq _P x \leq _P p_m$
. Similarly,
![]() $a_s \nleq _P p_m$
because otherwise we would have the contradiction
$a_s \nleq _P p_m$
because otherwise we would have the contradiction
![]() $a_{\ell } \leq _P a_s \leq _P p_m$
. Therefore either
$a_{\ell } \leq _P a_s \leq _P p_m$
. Therefore either
![]() $x>_P p_m$
or
$x>_P p_m$
or
![]() $a_s>_P p_m$
.
$a_s>_P p_m$
.
If
![]() $x>_P p_m$
, then x satisfies
$x>_P p_m$
, then x satisfies
![]() $x>_P p_m$
,
$x>_P p_m$
,
![]() $x \geq _P a_{\ell } \geq _P a_{m+1}$
, and
$x \geq _P a_{\ell } \geq _P a_{m+1}$
, and
![]() $x \mid _P a_s$
. That is, there are an
$x \mid _P a_s$
. That is, there are an
![]() $n> m+1$
and a
$n> m+1$
and a
![]() $p_{m+1} \in P$
with
$p_{m+1} \in P$
with
![]() $p_{m+1}>_P p_m$
,
$p_{m+1}>_P p_m$
,
![]() $p_{m+1} \geq _P a_{m+1}$
, and
$p_{m+1} \geq _P a_{m+1}$
, and
![]() $p_{m+1} \mid _P a_n$
. So
$p_{m+1} \mid _P a_n$
. So
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1)$
is defined.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1)$
is defined.
Otherwise
![]() $a_s>_P p_m$
. In this case, again by assumption there are a
$a_s>_P p_m$
. In this case, again by assumption there are a
![]() $t> s$
and a
$t> s$
and a
![]() $y \in P$
with
$y \in P$
with
This y satisfies
![]() $y \geq _P a_s>_P p_m$
,
$y \geq _P a_s>_P p_m$
,
![]() $y \geq _P a_s \geq _P a_{m+1}$
, and
$y \geq _P a_s \geq _P a_{m+1}$
, and
![]() $y \mid _P a_t$
. That is, there are an
$y \mid _P a_t$
. That is, there are an
![]() $n> m+1$
and a
$n> m+1$
and a
![]() $p_{m+1} \in P$
with
$p_{m+1} \in P$
with
![]() $p_{m+1}>_P p_m$
,
$p_{m+1}>_P p_m$
,
![]() $p_{m+1} \geq _P a_{m+1}$
, and
$p_{m+1} \geq _P a_{m+1}$
, and
![]() $p_{m+1} \mid _P a_n$
. So
$p_{m+1} \mid _P a_n$
. So
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1)$
is defined.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(A)(m+1)$
is defined.
Theorem 5.11.
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
.
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2} + \mathsf {ADS} \vdash (0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
.
Proof Let
![]() $(P, <_P)$
be an infinite partial order of width
$(P, <_P)$
be an infinite partial order of width
![]() $\leq \! 2$
.
$\leq \! 2$
.
![]() $\mathsf {RCA}_0 \vdash \mathsf {CC}_2$
by Proposition 3.8, so we may apply
$\mathsf {RCA}_0 \vdash \mathsf {CC}_2$
by Proposition 3.8, so we may apply
![]() $\mathsf {CC}_2$
to P to obtain an infinite chain C. Apply
$\mathsf {CC}_2$
to P to obtain an infinite chain C. Apply
![]() $\mathsf {ADS}$
to C to obtain either an infinite ascending sequence or an infinite descending sequence in C. By reversing P if necessary, we may assume that P contains an infinite ascending sequence
$\mathsf {ADS}$
to C to obtain either an infinite ascending sequence or an infinite descending sequence in C. By reversing P if necessary, we may assume that P contains an infinite ascending sequence
![]() $A = \langle a_n : n \in \mathbb {N} \rangle $
.
$A = \langle a_n : n \in \mathbb {N} \rangle $
.
Let
![]() $\vec {P} = P \oplus {<_P}$
, and let
$\vec {P} = P \oplus {<_P}$
, and let
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \rightarrow P^{\mathbb {N}}$
be the Turing functional relative to
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}} \colon P^{\mathbb {N}} \rightarrow P^{\mathbb {N}}$
be the Turing functional relative to
![]() $\vec {P}$
from Lemma 5.10. Let
$\vec {P}$
from Lemma 5.10. Let
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}$
denote the i
th iteration of
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}$
denote the i
th iteration of
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}$
given by
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}$
given by
 $$ \begin{align*} \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, 0}(A) &= A,\\ \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, i+1}(A) &= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}, i}(A)). \end{align*} $$
$$ \begin{align*} \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, 0}(A) &= A,\\ \operatorname{{\mathrm{FindLadder}}}^{\vec{P}, i+1}(A) &= \operatorname{{\mathrm{FindLadder}}}^{\vec{P}}(\operatorname{{\mathrm{FindLadder}}}^{\vec{P}, i}(A)). \end{align*} $$
There are two cases: either
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is partial for some i, or
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is partial for some i, or
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is total for all i.
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is total for all i.
First suppose that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is partial for some i. Then, by
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is partial for some i. Then, by
![]() $\mathsf {I}\Sigma ^0_{2}$
in the form of the
$\mathsf {I}\Sigma ^0_{2}$
in the form of the
![]() $\Sigma ^0_2$
least element principle, there is a least i such that
$\Sigma ^0_2$
least element principle, there is a least i such that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is partial. As
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is partial. As
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, 0}(A)$
is total, it must be that
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, 0}(A)$
is total, it must be that
![]() $i> 0$
and that
$i> 0$
and that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)$
is total. Then
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)$
is total. Then
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)$
computes an infinite ascending sequence in P because either
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)$
computes an infinite ascending sequence in P because either
![]() $i-1 = 0$
, in which case
$i-1 = 0$
, in which case
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)$
is A; or
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)$
is A; or
![]() $i-1> 0$
, in which case
$i-1> 0$
, in which case
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A) = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-2}(A))$
computes an infinite ascending sequence by Lemma 5.10 item (2). Let
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A) = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}}(\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-2}(A))$
computes an infinite ascending sequence by Lemma 5.10 item (2). Let
![]() $B = \langle b_n : n \in \mathbb {N} \rangle $
denote the infinite ascending sequence computed by
$B = \langle b_n : n \in \mathbb {N} \rangle $
denote the infinite ascending sequence computed by
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)$
, where
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)$
, where
![]() $b_n = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)(n)$
for each n. We claim that some tail of B is
$b_n = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i-1}(A)(n)$
for each n. We claim that some tail of B is
![]() $(0,\infty )$
-homogeneous. If not, then every tail of B has a counterexample, which implies that
$(0,\infty )$
-homogeneous. If not, then every tail of B has a counterexample, which implies that
Therefore,
is total by Lemma 5.10 item (1). This contradicts that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is partial. Therefore some tail
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is partial. Therefore some tail
![]() $B_{\geq n}$
of B is
$B_{\geq n}$
of B is
![]() $(0,\infty )$
-homogeneous. Ascending
$(0,\infty )$
-homogeneous. Ascending
![]() $(0,\infty )$
-homogeneous sequences are necessarily
$(0,\infty )$
-homogeneous sequences are necessarily
![]() $(0,\mathrm {cof})$
-homogeneous, and infinite subsets of
$(0,\mathrm {cof})$
-homogeneous, and infinite subsets of
![]() $(0,\mathrm {cof})$
-homogeneous chains are necessarily
$(0,\mathrm {cof})$
-homogeneous chains are necessarily
![]() $(0,\mathrm {cof})$
-homogeneous as well. Thus we may thin
$(0,\mathrm {cof})$
-homogeneous as well. Thus we may thin
![]() $B_{\geq n}$
to an infinite sequence whose range exists as a set and thereby obtain a
$B_{\geq n}$
to an infinite sequence whose range exists as a set and thereby obtain a
![]() $(0,\mathrm {cof})$
-homogeneous chain for P.
$(0,\mathrm {cof})$
-homogeneous chain for P.
Now suppose that
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is total for all i. Then the sequence
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is total for all i. Then the sequence
![]() $(\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A) : i \in \mathbb {N})$
is uniformly computable. Let
$(\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A) : i \in \mathbb {N})$
is uniformly computable. Let
![]() $A_i = \langle a^i_n : n \in \mathbb {N} \rangle $
denote the infinite sequence computed by
$A_i = \langle a^i_n : n \in \mathbb {N} \rangle $
denote the infinite sequence computed by
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
, where
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
, where
![]() $a^i_n = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)(n)$
for all i and n. For every i,
$a^i_n = \operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)(n)$
for all i and n. For every i,
![]() $A_i$
is an infinite ascending sequence in P and
$A_i$
is an infinite ascending sequence in P and
![]() $A_{i+1}$
is a ladder for
$A_{i+1}$
is a ladder for
![]() $A_i$
by the fact that
$A_i$
by the fact that
![]() $A_0 = A$
, by the assumption that every
$A_0 = A$
, by the assumption that every
![]() $\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is total, and by Lemma 5.10 item (2). We have that for every
$\operatorname {{\mathrm {FindLadder}}}^{\vec {P}, i}(A)$
is total, and by Lemma 5.10 item (2). We have that for every
![]() $i_0, i_1, n_0, n_1$
, if
$i_0, i_1, n_0, n_1$
, if
![]() $i_0 \leq i_1$
and
$i_0 \leq i_1$
and
![]() $n_0 \leq n_1$
, then
$n_0 \leq n_1$
, then
![]() $a^{i_0}_{n_0} \leq _P a^{i_1}_{n_1}$
. This is because
$a^{i_0}_{n_0} \leq _P a^{i_1}_{n_1}$
. This is because
The inequality
![]() $a^{i_0}_{n_0} \leq _P a^{i_0}_{n_1}$
is because
$a^{i_0}_{n_0} \leq _P a^{i_0}_{n_1}$
is because
![]() $A_{i_0}$
is an ascending sequence. The inequalities
$A_{i_0}$
is an ascending sequence. The inequalities
![]() $a^{i_0}_{n_1} \leq _P a^{i_0 + 1}_{n_1} \leq _P \cdots \leq _P a^{i_1}_{n_1}$
are because
$a^{i_0}_{n_1} \leq _P a^{i_0 + 1}_{n_1} \leq _P \cdots \leq _P a^{i_1}_{n_1}$
are because
![]() $A_{i+1}$
is a ladder for
$A_{i+1}$
is a ladder for
![]() $A_i$
for each i. Additionally, if
$A_i$
for each i. Additionally, if
![]() $n_0 < n_1$
, then the inequality
$n_0 < n_1$
, then the inequality
![]() $a^{i_0}_{n_0} <_P a^{i_0}_{n_1}$
is strict and therefore the inequality
$a^{i_0}_{n_0} <_P a^{i_0}_{n_1}$
is strict and therefore the inequality
![]() $a^{i_0}_{n_0} <_P a^{i_1}_{n_1}$
is strict as well.
$a^{i_0}_{n_0} <_P a^{i_1}_{n_1}$
is strict as well.
Define an infinite sequence
![]() $B = \langle b_i : i \in \mathbb {N} \rangle $
by
$B = \langle b_i : i \in \mathbb {N} \rangle $
by
![]() $b_i = a^i_i$
for each i. The sequence B is ascending in P because
$b_i = a^i_i$
for each i. The sequence B is ascending in P because
![]() $a_i^i <_P a_{i+1}^{i+1}$
for each i. The ascending sequence B is also
$a_i^i <_P a_{i+1}^{i+1}$
for each i. The ascending sequence B is also
![]() $(0,\mathrm {cof})$
-homogeneous. To see this, consider a
$(0,\mathrm {cof})$
-homogeneous. To see this, consider a
![]() $p \in P$
such that
$p \in P$
such that
![]() $p \nleq _P b_i$
for all i. We show that
$p \nleq _P b_i$
for all i. We show that
![]() $p \geq _P b_i$
for all i. Given i, there is an
$p \geq _P b_i$
for all i. Given i, there is an
![]() $n> i+1$
with
$n> i+1$
with
![]() $a^{i+1}_{i+1} \mid _P a^i_n$
by Lemma 5.10 item (2). The element p is comparable either with
$a^{i+1}_{i+1} \mid _P a^i_n$
by Lemma 5.10 item (2). The element p is comparable either with
![]() $b_{i+1} = a^{i+1}_{i+1}$
or with
$b_{i+1} = a^{i+1}_{i+1}$
or with
![]() $a^i_n$
because P has width
$a^i_n$
because P has width
![]() $\leq 2$
. We have that
$\leq 2$
. We have that
![]() $p \nleq _P b_{i+1}$
by assumption and that
$p \nleq _P b_{i+1}$
by assumption and that
![]() $p \nleq _P a^i_n$
because
$p \nleq _P a^i_n$
because
![]() $p \leq _P a^i_n$
yields the contradiction
$p \leq _P a^i_n$
yields the contradiction
![]() $p \leq _P a^i_n \leq _P a^n_n = b_n$
. Thus either
$p \leq _P a^i_n \leq _P a^n_n = b_n$
. Thus either
![]() $p \geq _P b_{i+1} \geq _P b_i$
or
$p \geq _P b_{i+1} \geq _P b_i$
or
![]() $p \geq _P a^i_n \geq _P a^i_i = b_i$
. Therefore
$p \geq _P a^i_n \geq _P a^i_i = b_i$
. Therefore
![]() $p \geq _P b_i$
, as desired. Thus every
$p \geq _P b_i$
, as desired. Thus every
![]() $p \in P$
is either below some element of B, in which case it is below almost every element of B because B is an ascending sequence; or is above all elements of B. So B is a
$p \in P$
is either below some element of B, in which case it is below almost every element of B because B is an ascending sequence; or is above all elements of B. So B is a
![]() $(0,\mathrm {cof})$
-homogeneous ascending sequence. As above, we may thin B to an infinite sequence whose range exists as a set and thereby obtain a
$(0,\mathrm {cof})$
-homogeneous ascending sequence. As above, we may thin B to an infinite sequence whose range exists as a set and thereby obtain a
![]() $(0,\mathrm {cof})$
-homogeneous chain for P.
$(0,\mathrm {cof})$
-homogeneous chain for P.
Unfortunately, the method of Theorem 5.11 does not appear to readily generalize even to
![]() $3$
-chain decomposable partial orders.
$3$
-chain decomposable partial orders.
6 Reversals and equivalences
We supply the following reversals:
-
•
 $\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_3 \vdash \mathsf {ADS}$
(Lemma 6.1).
$\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_3 \vdash \mathsf {ADS}$
(Lemma 6.1). -
•
 $\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_2 \vdash \mathsf {SADS}$
(Lemma 6.2).
$\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_2 \vdash \mathsf {SADS}$
(Lemma 6.2). -
•
 $\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty } \vdash \mathsf {I}\Sigma ^0_{2}$
(Lemma 6.3).
$\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty } \vdash \mathsf {I}\Sigma ^0_{2}$
(Lemma 6.3). -
•
 $\mathsf {RCA}_0 + (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2 \vdash \mathsf {ADS}$
(Lemma 6.4).
$\mathsf {RCA}_0 + (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2 \vdash \mathsf {ADS}$
(Lemma 6.4).
Theorem 6.6 then combines these reversals with the results of the previous section in order to characterize the axiomatic strength of several versions of the Rival–Sands theorem for partial orders. We also present a few questions.
Lemma 6.1.
![]() $\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_3 \vdash \mathsf {ADS}$
.
$\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_3 \vdash \mathsf {ADS}$
.
Proof Let
![]() $(L, <_L)$
be an infinite linear order. Let
$(L, <_L)$
be an infinite linear order. Let
![]() $(Q, <_Q)$
be the three-element partial order
$(Q, <_Q)$
be the three-element partial order
![]() $Q = \{a, b, z\}$
with
$Q = \{a, b, z\}$
with
![]() $a, b <_Q z$
and
$a, b <_Q z$
and
![]() $a \mid _Q b$
. Consider the product partial order
$a \mid _Q b$
. Consider the product partial order
![]() $(P, <_P)$
, where
$(P, <_P)$
, where
![]() $P = L \times Q$
and
$P = L \times Q$
and
![]() $\langle \ell _0, q_0 \rangle \leq _P \langle \ell _1, q_1 \rangle $
if and only if
$\langle \ell _0, q_0 \rangle \leq _P \langle \ell _1, q_1 \rangle $
if and only if
![]() $\ell _0 \leq _L \ell _1$
and
$\ell _0 \leq _L \ell _1$
and
![]() $q_0 \leq _Q q_1$
. The partial order P has the
$q_0 \leq _Q q_1$
. The partial order P has the
![]() $3$
-chain decomposition
$3$
-chain decomposition
![]() $C_a = L \times \{a\}$
,
$C_a = L \times \{a\}$
,
![]() $C_b = L \times \{b\}$
,
$C_b = L \times \{b\}$
,
![]() $C_z = L \times \{z\}$
. Thus by
$C_z = L \times \{z\}$
. Thus by
![]() $\mathsf {RSpo}^{\mathsf {CD}}_3$
, let C be a
$\mathsf {RSpo}^{\mathsf {CD}}_3$
, let C be a
![]() $(0,\infty )$
-homogeneous chain for P.
$(0,\infty )$
-homogeneous chain for P.
Notice that C cannot intersect both
![]() $C_a$
and
$C_a$
and
![]() $C_b$
because
$C_b$
because
![]() $\langle \ell _0, a \rangle \mid _P \langle \ell _1, b \rangle $
for every
$\langle \ell _0, a \rangle \mid _P \langle \ell _1, b \rangle $
for every
![]() $\ell _0, \ell _1 \in L$
. Thus either
$\ell _0, \ell _1 \in L$
. Thus either
![]() $C \subseteq C_a \cup C_z$
or
$C \subseteq C_a \cup C_z$
or
![]() $C \subseteq C_b \cup C_z$
. Assume for the sake of argument that
$C \subseteq C_b \cup C_z$
. Assume for the sake of argument that
![]() $C \subseteq C_a \cup C_z$
. The
$C \subseteq C_a \cup C_z$
. The
![]() $C \subseteq C_b \cup C_z$
case is symmetric.
$C \subseteq C_b \cup C_z$
case is symmetric.
We claim that
![]() $C \cap C_z$
has no maximum element. Suppose for a contradiction that
$C \cap C_z$
has no maximum element. Suppose for a contradiction that
![]() $\langle m, z \rangle $
is the maximum element of
$\langle m, z \rangle $
is the maximum element of
![]() $C \cap C_z$
, and consider the element
$C \cap C_z$
, and consider the element
![]() $\langle m, b \rangle $
. Then
$\langle m, b \rangle $
. Then
![]() $\langle m, b \rangle <_Q \langle m, z \rangle $
. However, every other element of C is either of the form
$\langle m, b \rangle <_Q \langle m, z \rangle $
. However, every other element of C is either of the form
![]() $\langle \ell , a \rangle $
, in which case
$\langle \ell , a \rangle $
, in which case
![]() $\langle m, b \rangle \mid _P \langle \ell , a \rangle $
because
$\langle m, b \rangle \mid _P \langle \ell , a \rangle $
because
![]() $b \mid _Q a$
; or of the form
$b \mid _Q a$
; or of the form
![]() $\langle \ell , z \rangle $
with
$\langle \ell , z \rangle $
with
![]() $\ell <_L m$
, in which case
$\ell <_L m$
, in which case
![]() $\langle m, b \rangle \mid _P \langle \ell , z \rangle $
because
$\langle m, b \rangle \mid _P \langle \ell , z \rangle $
because
![]() $m>_L \ell $
and
$m>_L \ell $
and
![]() $b <_Q z$
. Thus
$b <_Q z$
. Thus
![]() $\langle m, b \rangle $
is comparable with exactly one element of C, contradicting that C is
$\langle m, b \rangle $
is comparable with exactly one element of C, contradicting that C is
![]() $(0,\infty )$
-homogeneous.
$(0,\infty )$
-homogeneous.
If
![]() $C \cap C_z \neq \emptyset $
, then
$C \cap C_z \neq \emptyset $
, then
![]() $C \cap C_z$
is non-empty and has no maximum element, so we can define an infinite ascending sequence
$C \cap C_z$
is non-empty and has no maximum element, so we can define an infinite ascending sequence
![]() $\langle \ell _0, z \rangle <_P \langle \ell _1, z \rangle <_P \langle \ell _2, z \rangle <_P \cdots $
in
$\langle \ell _0, z \rangle <_P \langle \ell _1, z \rangle <_P \langle \ell _2, z \rangle <_P \cdots $
in
![]() $C \cap C_z$
. This yields an infinite ascending sequence
$C \cap C_z$
. This yields an infinite ascending sequence
![]() $\ell _0 <_L \ell _1 <_L \ell _2 <_L \cdots $
in L.
$\ell _0 <_L \ell _1 <_L \ell _2 <_L \cdots $
in L.
If
![]() $C \cap C_z = \emptyset $
, then
$C \cap C_z = \emptyset $
, then
![]() $C \subseteq C_a$
. In this case, we claim that C has no minimum element. Suppose for a contradiction that
$C \subseteq C_a$
. In this case, we claim that C has no minimum element. Suppose for a contradiction that
![]() $\langle m, a \rangle $
is the minimum element of C, and consider the element
$\langle m, a \rangle $
is the minimum element of C, and consider the element
![]() $\langle m, z \rangle $
. Then
$\langle m, z \rangle $
. Then
![]() $\langle m, a \rangle <_P \langle m, z \rangle $
. However, every other element of C is of the form
$\langle m, a \rangle <_P \langle m, z \rangle $
. However, every other element of C is of the form
![]() $\langle \ell , a \rangle $
with
$\langle \ell , a \rangle $
with
![]() $m <_L \ell $
, in which case
$m <_L \ell $
, in which case
![]() $\langle m, z \rangle \mid _P \langle \ell , a \rangle $
because
$\langle m, z \rangle \mid _P \langle \ell , a \rangle $
because
![]() $m <_L \ell $
and
$m <_L \ell $
and
![]() $z>_Q a$
. Thus
$z>_Q a$
. Thus
![]() $\langle m, z \rangle $
is comparable with exactly one element of C, contradicting that C is
$\langle m, z \rangle $
is comparable with exactly one element of C, contradicting that C is
![]() $(0,\infty )$
-homogeneous. We may now define an infinite descending sequence
$(0,\infty )$
-homogeneous. We may now define an infinite descending sequence
![]() $\langle \ell _0, a \rangle>_P \langle \ell _1, a \rangle >_P \langle \ell _2, a \rangle >_P \cdots $
in C and hence an infinite descending sequence
$\langle \ell _0, a \rangle>_P \langle \ell _1, a \rangle >_P \langle \ell _2, a \rangle >_P \cdots $
in C and hence an infinite descending sequence
![]() $\ell _0>_L \ell _1 >_L \ell _2 >_L \cdots $
in L.
$\ell _0>_L \ell _1 >_L \ell _2 >_L \cdots $
in L.
Thus L has either an infinite ascending sequence or an infinite descending sequence.
Lemma 6.2.
![]() $\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_2 \vdash \mathsf {SADS}$
.
$\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_2 \vdash \mathsf {SADS}$
.
Proof Let
![]() $(L, <_L)$
be an infinite stable linear order. Let
$(L, <_L)$
be an infinite stable linear order. Let
![]() $(Q, <_Q)$
be the two-element linear order
$(Q, <_Q)$
be the two-element linear order
![]() $Q = \{a, z\}$
with
$Q = \{a, z\}$
with
![]() $a <_Q z$
, and let
$a <_Q z$
, and let
![]() $(P, <_P)$
be the product partial order
$(P, <_P)$
be the product partial order
![]() $L \times Q$
. The partial order P has the
$L \times Q$
. The partial order P has the
![]() $2$
-chain decomposition
$2$
-chain decomposition
![]() $C_a = L \times \{a\}$
,
$C_a = L \times \{a\}$
,
![]() $C_z = L \times \{z\}$
. Thus by
$C_z = L \times \{z\}$
. Thus by
![]() $\mathsf {RSpo}^{\mathsf {CD}}_2$
, let C be a
$\mathsf {RSpo}^{\mathsf {CD}}_2$
, let C be a
![]() $(0,\infty )$
-homogeneous chain for P.
$(0,\infty )$
-homogeneous chain for P.
The linear order L is stable, so every
![]() $\ell \in L$
has either finitely many
$\ell \in L$
has either finitely many
![]() $<_L$
-predecessors or finitely many
$<_L$
-predecessors or finitely many
![]() $<_L$
-successors. We claim that
$<_L$
-successors. We claim that
![]() $C \cap C_a$
cannot contain two elements
$C \cap C_a$
cannot contain two elements
![]() $\langle \ell , a \rangle $
and
$\langle \ell , a \rangle $
and
![]() $\langle r, a \rangle $
where
$\langle r, a \rangle $
where
![]() $\ell $
has only finitely many
$\ell $
has only finitely many
![]() $<_L$
-predecessors and r has only finitely many
$<_L$
-predecessors and r has only finitely many
![]() $<_L$
-successors. Suppose for a contradiction that
$<_L$
-successors. Suppose for a contradiction that
![]() $C \cap C_a$
does contain such an
$C \cap C_a$
does contain such an
![]() $\langle \ell , a \rangle $
and
$\langle \ell , a \rangle $
and
![]() $\langle r, a \rangle $
, and consider the element
$\langle r, a \rangle $
, and consider the element
![]() $\langle \ell , z \rangle $
. The element
$\langle \ell , z \rangle $
. The element
![]() $\langle \ell , z \rangle $
is comparable with an
$\langle \ell , z \rangle $
is comparable with an
![]() $\langle x, a \rangle \in C_a$
if and only if
$\langle x, a \rangle \in C_a$
if and only if
![]() $x \leq _L \ell $
, and there are only finitely many such elements
$x \leq _L \ell $
, and there are only finitely many such elements
![]() $x \in L$
. Thus
$x \in L$
. Thus
![]() $\langle \ell , z \rangle $
is comparable with only finitely many elements of
$\langle \ell , z \rangle $
is comparable with only finitely many elements of
![]() $C \cap C_a$
. On the other hand, the element
$C \cap C_a$
. On the other hand, the element
![]() $\langle r, a \rangle $
is comparable with an
$\langle r, a \rangle $
is comparable with an
![]() $\langle x, z \rangle \in C_z$
if and only if
$\langle x, z \rangle \in C_z$
if and only if
![]() $r \leq _L x$
, and there are only finitely many such elements
$r \leq _L x$
, and there are only finitely many such elements
![]() $x \in L$
. Thus
$x \in L$
. Thus
![]() $C \cap C_z$
is finite because all of its elements are comparable with
$C \cap C_z$
is finite because all of its elements are comparable with
![]() $\langle r, a \rangle $
. It follows that
$\langle r, a \rangle $
. It follows that
![]() $\langle \ell , z \rangle $
is comparable with
$\langle \ell , z \rangle $
is comparable with
![]() $\langle \ell , a \rangle \in C$
and is comparable with only finitely many elements of C in total. This contradicts that C is
$\langle \ell , a \rangle \in C$
and is comparable with only finitely many elements of C in total. This contradicts that C is
![]() $(0,\infty )$
-homogeneous for P. Symmetric reasoning shows that
$(0,\infty )$
-homogeneous for P. Symmetric reasoning shows that
![]() $C \cap C_z$
also cannot contain two elements
$C \cap C_z$
also cannot contain two elements
![]() $\langle \ell , z \rangle $
and
$\langle \ell , z \rangle $
and
![]() $\langle r, z \rangle $
where
$\langle r, z \rangle $
where
![]() $\ell $
has only finitely many
$\ell $
has only finitely many
![]() $<_L$
-predecessors and r has only finitely many
$<_L$
-predecessors and r has only finitely many
![]() $<_L$
-successors.
$<_L$
-successors.
The chain C is infinite, so either
![]() $C \cap C_a$
is infinite or
$C \cap C_a$
is infinite or
![]() $C \cap C_z$
is infinite. Suppose for the sake of argument that
$C \cap C_z$
is infinite. Suppose for the sake of argument that
![]() $C \cap C_a$
is infinite. The other case is symmetric. By the claim above, it must be that either
$C \cap C_a$
is infinite. The other case is symmetric. By the claim above, it must be that either
![]() $\ell $
has only finitely many
$\ell $
has only finitely many
![]() $<_L$
-predecessors whenever
$<_L$
-predecessors whenever
![]() $\langle \ell , a \rangle \in C \cap C_a$
or that
$\langle \ell , a \rangle \in C \cap C_a$
or that
![]() $\ell $
has only finitely many
$\ell $
has only finitely many
![]() $<_L$
-successors whenever
$<_L$
-successors whenever
![]() $\langle \ell , a \rangle \in C \cap C_a$
. Suppose that
$\langle \ell , a \rangle \in C \cap C_a$
. Suppose that
![]() $\ell $
has only finitely many
$\ell $
has only finitely many
![]() $<_L$
-predecessors whenever
$<_L$
-predecessors whenever
![]() $\langle \ell , a \rangle \in C \cap C_a$
. Then for every
$\langle \ell , a \rangle \in C \cap C_a$
. Then for every
![]() $\langle \ell , a \rangle \in C \cap C_a$
, there is an
$\langle \ell , a \rangle \in C \cap C_a$
, there is an
![]() $\langle r, a \rangle \in C \cap C_a$
with
$\langle r, a \rangle \in C \cap C_a$
with
![]() $\langle \ell , a \rangle <_P \langle r, a \rangle $
. We may thus define an infinite ascending sequence
$\langle \ell , a \rangle <_P \langle r, a \rangle $
. We may thus define an infinite ascending sequence
![]() $\langle \ell _0, a \rangle <_P \langle \ell _1, a \rangle <_P \langle \ell _2, a \rangle <_P \cdots $
in
$\langle \ell _0, a \rangle <_P \langle \ell _1, a \rangle <_P \langle \ell _2, a \rangle <_P \cdots $
in
![]() $C \cap C_a$
and hence an infinite ascending sequence
$C \cap C_a$
and hence an infinite ascending sequence
![]() $\ell _0 <_L \ell _1 <_L \ell _2 <_L \cdots $
in L. Similarly, if
$\ell _0 <_L \ell _1 <_L \ell _2 <_L \cdots $
in L. Similarly, if
![]() $\ell $
has only finitely many
$\ell $
has only finitely many
![]() $<_L$
-successors whenever
$<_L$
-successors whenever
![]() $\langle \ell , a \rangle \in C \cap C_a$
, then for every
$\langle \ell , a \rangle \in C \cap C_a$
, then for every
![]() $\langle \ell , a \rangle \in C \cap C_a$
, there is an
$\langle \ell , a \rangle \in C \cap C_a$
, there is an
![]() $\langle r, a \rangle \in C \cap C_a$
with
$\langle r, a \rangle \in C \cap C_a$
with
![]() $\langle r, a \rangle <_P \langle \ell , a \rangle $
. We may thus define an infinite descending sequence
$\langle r, a \rangle <_P \langle \ell , a \rangle $
. We may thus define an infinite descending sequence
![]() $\langle \ell _0, a \rangle>_P \langle \ell _1, a \rangle >_P \langle \ell _2, a \rangle >_P \cdots $
in
$\langle \ell _0, a \rangle>_P \langle \ell _1, a \rangle >_P \langle \ell _2, a \rangle >_P \cdots $
in
![]() $C \cap C_a$
and hence an infinite descending sequence
$C \cap C_a$
and hence an infinite descending sequence
![]() $\ell _0>_L \ell _1 >_L \ell _2 >_L \cdots $
in L. Thus L has either an infinite ascending sequence or an infinite descending sequence.
$\ell _0>_L \ell _1 >_L \ell _2 >_L \cdots $
in L. Thus L has either an infinite ascending sequence or an infinite descending sequence.
Lemma 6.3.
![]() $\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty } \vdash \mathsf {I}\Sigma ^0_{2}$
.
$\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty } \vdash \mathsf {I}\Sigma ^0_{2}$
.
Proof We show that
![]() $\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
proves the
$\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
proves the
![]() $\Pi ^0_2$
least element principle, which is equivalent to
$\Pi ^0_2$
least element principle, which is equivalent to
![]() $\mathsf {I}\Sigma ^0_{2}$
over
$\mathsf {I}\Sigma ^0_{2}$
over
![]() $\mathsf {RCA}_0$
as explained in Section 2. Notice that
$\mathsf {RCA}_0$
as explained in Section 2. Notice that
![]() $\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty } \vdash \mathsf {B}\Sigma ^0_{2}$
because
$\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty } \vdash \mathsf {B}\Sigma ^0_{2}$
because
![]() $\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty } \vdash \mathsf {ADS}$
by Lemma 6.1, and
$\mathsf {RCA}_0 + \mathsf {RSpo}^{\mathsf {CD}}_{<\infty } \vdash \mathsf {ADS}$
by Lemma 6.1, and
![]() $\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {B}\Sigma ^0_{2}$
as explained in Section 2. Thus we may make use of
$\mathsf {RCA}_0 + \mathsf {ADS} \vdash \mathsf {B}\Sigma ^0_{2}$
as explained in Section 2. Thus we may make use of
![]() $\mathsf {RT}^1_{<\infty }$
in the following argument.
$\mathsf {RT}^1_{<\infty }$
in the following argument.
Let
![]() $\forall x \, \exists y \, \varphi (n, x, y)$
be a
$\forall x \, \exists y \, \varphi (n, x, y)$
be a
![]() $\Pi ^0_2$
formula, possibly with undisplayed parameters, where
$\Pi ^0_2$
formula, possibly with undisplayed parameters, where
![]() $\varphi $
is
$\varphi $
is
![]() $\Sigma ^0_0$
. Let n be such that
$\Sigma ^0_0$
. Let n be such that
![]() $\forall x \, \exists y \, \varphi (n, x, y)$
. We want to find the least i such that
$\forall x \, \exists y \, \varphi (n, x, y)$
. We want to find the least i such that
![]() $\forall x \, \exists y \, \varphi (i, x, y)$
. Define a partial order
$\forall x \, \exists y \, \varphi (i, x, y)$
. Define a partial order
![]() $(P, <_P)$
by
$(P, <_P)$
by
and
That is, P consists of all triples
![]() $\langle i, s, t \rangle $
where
$\langle i, s, t \rangle $
where
![]() $i \leq n$
and t is least such that
$i \leq n$
and t is least such that
![]() $\forall x \leq s \; \exists y \leq t \; \varphi (i,x,y)$
. Notice that given i and s, there is at most one t with
$\forall x \leq s \; \exists y \leq t \; \varphi (i,x,y)$
. Notice that given i and s, there is at most one t with
![]() $\langle i, s, t \rangle \in P$
.
$\langle i, s, t \rangle \in P$
.
By assumption,
![]() $\forall x \, \exists y \, \varphi (n, x, y)$
. Thus given any s, we have that
$\forall x \, \exists y \, \varphi (n, x, y)$
. Thus given any s, we have that
![]() $\forall x \leq s \; \exists y \; \varphi (n, x, y)$
, and therefore by
$\forall x \leq s \; \exists y \; \varphi (n, x, y)$
, and therefore by
![]() $\mathsf {B}\Sigma ^0_{0}$
there is a t such that
$\mathsf {B}\Sigma ^0_{0}$
there is a t such that
![]() $\forall x \leq s \; \exists y \leq t \; \varphi (n, x, y)$
. Moreover, there is a least such t by the
$\forall x \leq s \; \exists y \leq t \; \varphi (n, x, y)$
. Moreover, there is a least such t by the
![]() $\Sigma ^0_0$
least element principle. This shows that for every s there is a t with
$\Sigma ^0_0$
least element principle. This shows that for every s there is a t with
![]() $\langle n, s, t \rangle \in P$
. Therefore P is infinite. Furthermore, P has the
$\langle n, s, t \rangle \in P$
. Therefore P is infinite. Furthermore, P has the
![]() $(n+1)$
-chain decomposition
$(n+1)$
-chain decomposition
![]() $C_0, \dots , C_n$
, where
$C_0, \dots , C_n$
, where
![]() $C_i = \{\langle i, s, t \rangle : \langle i, s, t \rangle \in P\}$
for each
$C_i = \{\langle i, s, t \rangle : \langle i, s, t \rangle \in P\}$
for each
![]() $i \leq n$
. By
$i \leq n$
. By
![]() $\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
, let C be a
$\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
, let C be a
![]() $(0,\infty )$
-homogeneous chain for P. By
$(0,\infty )$
-homogeneous chain for P. By
![]() $\mathsf {RT}^1_{<\infty }$
, there is an i such that
$\mathsf {RT}^1_{<\infty }$
, there is an i such that
![]() $C \cap C_i$
is infinite. We show that i is least such that
$C \cap C_i$
is infinite. We show that i is least such that
![]() $\forall x \, \exists y \, \varphi (i, x, y)$
.
$\forall x \, \exists y \, \varphi (i, x, y)$
.
First, as
![]() $C \cap C_i$
is infinite, given any
$C \cap C_i$
is infinite, given any
![]() $x_0$
there are an s and a t with
$x_0$
there are an s and a t with
![]() $\langle i, s, t \rangle \in P$
and
$\langle i, s, t \rangle \in P$
and
![]() $s \geq x_0$
. The fact that
$s \geq x_0$
. The fact that
![]() $\langle i, s, t \rangle \in P$
means that
$\langle i, s, t \rangle \in P$
means that
![]() $\forall x \leq s \; \exists y \leq t \; \varphi (i, x, y)$
. Thus
$\forall x \leq s \; \exists y \leq t \; \varphi (i, x, y)$
. Thus
![]() $\exists y \, \varphi (i, x_0, y)$
because
$\exists y \, \varphi (i, x_0, y)$
because
![]() $x_0 \leq s$
. Therefore
$x_0 \leq s$
. Therefore
![]() $\forall x \, \exists y \, \varphi (i, x, y)$
.
$\forall x \, \exists y \, \varphi (i, x, y)$
.
Second, if
![]() $j < i$
, then
$j < i$
, then
![]() $C \cap C_j = \emptyset $
. This is because for any
$C \cap C_j = \emptyset $
. This is because for any
![]() $\langle j, s_0, t_0 \rangle \in P$
, there is an
$\langle j, s_0, t_0 \rangle \in P$
, there is an
![]() $\langle i, s_1, t_1 \rangle \in C \cap C_i$
with
$\langle i, s_1, t_1 \rangle \in C \cap C_i$
with
![]() $s_1> s_0$
because
$s_1> s_0$
because
![]() $C \cap C_i$
is infinite. Then
$C \cap C_i$
is infinite. Then
![]() $\langle j, s_0, t_0 \rangle \mid _P \langle i, s_1, t_1 \rangle $
, so
$\langle j, s_0, t_0 \rangle \mid _P \langle i, s_1, t_1 \rangle $
, so
![]() $\langle j, s_0, t_0 \rangle \notin C$
because C is a chain. Now suppose for a contradiction that there is a
$\langle j, s_0, t_0 \rangle \notin C$
because C is a chain. Now suppose for a contradiction that there is a
![]() $j < i$
such that
$j < i$
such that
![]() $\forall x \, \exists y \, \varphi (j, x, y)$
. Let
$\forall x \, \exists y \, \varphi (j, x, y)$
. Let
![]() $\langle i, s_0, t_0 \rangle $
be any element of
$\langle i, s_0, t_0 \rangle $
be any element of
![]() $C \cap C_i$
. By the same argument as for n, the assumption
$C \cap C_i$
. By the same argument as for n, the assumption
![]() $\forall x \, \exists y \, \varphi (j, x, y)$
implies that for every s there is a t with
$\forall x \, \exists y \, \varphi (j, x, y)$
implies that for every s there is a t with
![]() $\langle j, s, t \rangle \in P$
. Therefore there is a
$\langle j, s, t \rangle \in P$
. Therefore there is a
![]() $t_1$
such that
$t_1$
such that
![]() $\langle j, s_0, t_1 \rangle \in P$
, and we have that
$\langle j, s_0, t_1 \rangle \in P$
, and we have that
![]() $\langle j, s_0, t_1 \rangle>_P \langle i, s_0, t_0 \rangle $
. However,
$\langle j, s_0, t_1 \rangle>_P \langle i, s_0, t_0 \rangle $
. However,
![]() $C \subseteq \bigcup _{k = i}^n C_k$
, and for
$C \subseteq \bigcup _{k = i}^n C_k$
, and for
![]() $\langle j, s_0, t_1 \rangle $
to be comparable with some
$\langle j, s_0, t_1 \rangle $
to be comparable with some
![]() $\langle k, s, t \rangle \in \bigcup _{k = i}^n C_k$
, it must be that
$\langle k, s, t \rangle \in \bigcup _{k = i}^n C_k$
, it must be that
![]() $s \leq s_0$
. There are only finitely many
$s \leq s_0$
. There are only finitely many
![]() $\langle k, s, t \rangle \in \bigcup _{k = i}^n C_k$
with
$\langle k, s, t \rangle \in \bigcup _{k = i}^n C_k$
with
![]() $s \leq s_0$
, so
$s \leq s_0$
, so
![]() $\langle j, s_0, t_1 \rangle $
is comparable with only finitely many elements of C. Thus
$\langle j, s_0, t_1 \rangle $
is comparable with only finitely many elements of C. Thus
![]() $\langle j, s_0, t_1 \rangle $
is comparable with
$\langle j, s_0, t_1 \rangle $
is comparable with
![]() $\langle i, s_0, t_0 \rangle \in C$
, but it is comparable with only finitely many elements of C in total. This contradicts that C is
$\langle i, s_0, t_0 \rangle \in C$
, but it is comparable with only finitely many elements of C in total. This contradicts that C is
![]() $(0,\infty )$
-homogeneous for P. Therefore we cannot have that
$(0,\infty )$
-homogeneous for P. Therefore we cannot have that
![]() $\forall x \, \exists y \, \varphi (j, x, y)$
, so i is least such that
$\forall x \, \exists y \, \varphi (j, x, y)$
, so i is least such that
![]() $\forall x \, \exists y \, \varphi (i, x, y)$
.
$\forall x \, \exists y \, \varphi (i, x, y)$
.
Lemma 6.4.
![]() $\mathsf {RCA}_0 + (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2 \vdash \mathsf {ADS}$
.
$\mathsf {RCA}_0 + (0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2 \vdash \mathsf {ADS}$
.
Proof Let
![]() $(L, <_L)$
be an infinite linear order. As in the proof of Lemma 6.2, let
$(L, <_L)$
be an infinite linear order. As in the proof of Lemma 6.2, let
![]() $(Q, <_Q)$
be the two-element linear order
$(Q, <_Q)$
be the two-element linear order
![]() $Q = \{a, z\}$
with
$Q = \{a, z\}$
with
![]() $a <_Q z$
, and let
$a <_Q z$
, and let
![]() $(P, <_P)$
be the product partial order
$(P, <_P)$
be the product partial order
![]() $L \times Q$
. The partial order P has the
$L \times Q$
. The partial order P has the
![]() $2$
-chain decomposition
$2$
-chain decomposition
![]() $C_a = L \times \{a\}$
,
$C_a = L \times \{a\}$
,
![]() $C_z = L \times \{z\}$
. Thus by
$C_z = L \times \{z\}$
. Thus by
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2$
, let C be a
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2$
, let C be a
![]() $(0,\mathrm {cof})$
-homogeneous chain for P.
$(0,\mathrm {cof})$
-homogeneous chain for P.
The chain C is infinite, so either
![]() $C \cap C_a$
is infinite or
$C \cap C_a$
is infinite or
![]() $C \cap C_z$
is infinite. First suppose that
$C \cap C_z$
is infinite. First suppose that
![]() $C \cap C_a$
is infinite. Then
$C \cap C_a$
is infinite. Then
![]() $C \cap C_a$
has no minimum element. Suppose for a contradiction that
$C \cap C_a$
has no minimum element. Suppose for a contradiction that
![]() $\langle m, a \rangle $
is the minimum element of
$\langle m, a \rangle $
is the minimum element of
![]() $C \cap C_a$
, and consider the element
$C \cap C_a$
, and consider the element
![]() $\langle m, z \rangle $
. Then
$\langle m, z \rangle $
. Then
![]() $\langle m, a \rangle <_P \langle m, z \rangle $
. However, every other element of
$\langle m, a \rangle <_P \langle m, z \rangle $
. However, every other element of
![]() $C \cap C_a$
is of the form
$C \cap C_a$
is of the form
![]() $\langle \ell , a \rangle $
with
$\langle \ell , a \rangle $
with
![]() $m <_L \ell $
, in which case
$m <_L \ell $
, in which case
![]() $\langle m, z \rangle \mid _P \langle \ell , a \rangle $
because
$\langle m, z \rangle \mid _P \langle \ell , a \rangle $
because
![]() $m <_L \ell $
and
$m <_L \ell $
and
![]() $z>_Q a$
. Thus
$z>_Q a$
. Thus
![]() $\langle m, z \rangle $
is comparable with at least one element of C, but it is not comparable with cofinitely many elements of C because it is incomparable with every element of
$\langle m, z \rangle $
is comparable with at least one element of C, but it is not comparable with cofinitely many elements of C because it is incomparable with every element of
![]() $C \cap C_a$
except
$C \cap C_a$
except
![]() $\langle m, a \rangle $
. This contradicts that C is
$\langle m, a \rangle $
. This contradicts that C is
![]() $(0,\mathrm {cof})$
-homogeneous for P. Thus
$(0,\mathrm {cof})$
-homogeneous for P. Thus
![]() $C \cap C_a$
is infinite and has no minimum element. We may therefore define an infinite descending sequence
$C \cap C_a$
is infinite and has no minimum element. We may therefore define an infinite descending sequence
![]() $\langle \ell _0, a \rangle>_P \langle \ell _1, a \rangle >_P \langle \ell _2, a \rangle >_P \cdots $
in
$\langle \ell _0, a \rangle>_P \langle \ell _1, a \rangle >_P \langle \ell _2, a \rangle >_P \cdots $
in
![]() $C \cap C_a$
and hence an infinite descending sequence
$C \cap C_a$
and hence an infinite descending sequence
![]() $\ell _0>_L \ell _1 >_L \ell _2 >_L \cdots $
in L.
$\ell _0>_L \ell _1 >_L \ell _2 >_L \cdots $
in L.
The case where
![]() $C \cap C_z$
is infinite is dual to the previous case. If
$C \cap C_z$
is infinite is dual to the previous case. If
![]() $C \cap C_z$
has maximum element
$C \cap C_z$
has maximum element
![]() $\langle m, z \rangle $
, then
$\langle m, z \rangle $
, then
![]() $\langle m, a \rangle $
witnesses that C is not
$\langle m, a \rangle $
witnesses that C is not
![]() $(0,\mathrm {cof})$
-homogeneous. Thus
$(0,\mathrm {cof})$
-homogeneous. Thus
![]() $C \cap C_z$
is infinite and has no maximum element. We may therefore define an infinite ascending sequence
$C \cap C_z$
is infinite and has no maximum element. We may therefore define an infinite ascending sequence
![]() $\langle \ell _0, z \rangle <_P \langle \ell _1, z \rangle <_P \langle \ell _2, z \rangle <_P \cdots $
in
$\langle \ell _0, z \rangle <_P \langle \ell _1, z \rangle <_P \langle \ell _2, z \rangle <_P \cdots $
in
![]() $C \cap C_z$
and hence an infinite ascending sequence
$C \cap C_z$
and hence an infinite ascending sequence
![]() $\ell _0 <_L \ell _1 <_L \ell _2 <_L \cdots $
in L.
$\ell _0 <_L \ell _1 <_L \ell _2 <_L \cdots $
in L.
Thus L has either an infinite ascending sequence or an infinite descending sequence.
Thus for
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
implies
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
implies
![]() $\mathsf {ADS}$
, which implies that every
$\mathsf {ADS}$
, which implies that every
![]() $(0,\mathrm {cof})$
-homogeneous chain in a partial order of width
$(0,\mathrm {cof})$
-homogeneous chain in a partial order of width
![]() $\leq \! k$
has a suborder of type either
$\leq \! k$
has a suborder of type either
![]() $\omega $
or
$\omega $
or
![]() $\omega ^*$
. We therefore have the following proposition.
$\omega ^*$
. We therefore have the following proposition.
Proposition 6.5.
![]() $\mathsf {RCA}_0$
proves the statement “For every
$\mathsf {RCA}_0$
proves the statement “For every
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
holds if and only if every infinite partial order of width
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
holds if and only if every infinite partial order of width
![]() $\leq \! k$
has a
$\leq \! k$
has a
![]() $(0,\infty )$
-homogeneous chain of order-type either
$(0,\infty )$
-homogeneous chain of order-type either
![]() $\omega $
or
$\omega $
or
![]() $\omega ^*$
.”
$\omega ^*$
.”
Proof Let
![]() $k \geq 2$
. In any partial order, a
$k \geq 2$
. In any partial order, a
![]() $(0,\infty )$
-homogeneous chain of order-type
$(0,\infty )$
-homogeneous chain of order-type
![]() $\omega $
or
$\omega $
or
![]() $\omega ^*$
is necessarily
$\omega ^*$
is necessarily
![]() $(0,\mathrm {cof})$
-homogeneous. Thus if every infinite partial order of width
$(0,\mathrm {cof})$
-homogeneous. Thus if every infinite partial order of width
![]() $\leq \! k$
has a
$\leq \! k$
has a
![]() $(0,\infty )$
-homogeneous chain of order-type either
$(0,\infty )$
-homogeneous chain of order-type either
![]() $\omega $
or
$\omega $
or
![]() $\omega ^*$
, then
$\omega ^*$
, then
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
holds. Conversely, suppose that
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
holds. Conversely, suppose that
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
holds. Then
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
holds. Then
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
holds because
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
holds because
![]() $k \geq 2$
, so
$k \geq 2$
, so
![]() $\mathsf {ADS}$
holds by Lemma 6.4. Let
$\mathsf {ADS}$
holds by Lemma 6.4. Let
![]() $(P, <_P)$
be an infinite partial order of width
$(P, <_P)$
be an infinite partial order of width
![]() $\leq \! k$
. Then P has a
$\leq \! k$
. Then P has a
![]() $(0,\mathrm {cof})$
-homogeneous chain C by
$(0,\mathrm {cof})$
-homogeneous chain C by
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
, and C has a suborder B of type either
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
, and C has a suborder B of type either
![]() $\omega $
or
$\omega $
or
![]() $\omega ^*$
by
$\omega ^*$
by
![]() $\mathsf {ADS}$
. The chain B is also
$\mathsf {ADS}$
. The chain B is also
![]() $(0,\mathrm {cof})$
-homogeneous, and therefore it is
$(0,\mathrm {cof})$
-homogeneous, and therefore it is
![]() $(0,\infty )$
-homogeneous. Thus B is a
$(0,\infty )$
-homogeneous. Thus B is a
![]() $(0,\infty )$
-homogeneous chain in P of order-type either
$(0,\infty )$
-homogeneous chain in P of order-type either
![]() $\omega $
or
$\omega $
or
![]() $\omega ^*$
.
$\omega ^*$
.
Of course, Proposition 6.5 also holds with
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_k$
and “that is k-chain decomposable” in place of
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_k$
and “that is k-chain decomposable” in place of
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
and “of width
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
and “of width
![]() $\leq \! k$
.”
$\leq \! k$
.”
The following theorem characterizes the strength the Rival–Sands theorem for partial orders.
Theorem 6.6.
-
(1)
 $\mathsf {RSpo}_{<\infty }$
,
$\mathsf {RSpo}_{<\infty }$
,
 $\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
, and
$\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
, and
 $\mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
are pairwise equivalent over
$\mathsf {I}\Sigma ^0_{2} + \mathsf {ADS}$
are pairwise equivalent over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
. -
(2) For each fixed standard
 $k \geq 3$
,
$k \geq 3$
,
 $\mathsf {RSpo}_k$
,
$\mathsf {RSpo}_k$
,
 $\mathsf {RSpo}^{\mathsf {CD}}_k$
, and
$\mathsf {RSpo}^{\mathsf {CD}}_k$
, and
 $\mathsf {ADS}$
are pairwise equivalent over
$\mathsf {ADS}$
are pairwise equivalent over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
. -
(3)
 $\mathsf {RSpo}^{\mathsf {CD}}_2$
and
$\mathsf {RSpo}^{\mathsf {CD}}_2$
and
 $\mathsf {SADS}$
are equivalent over
$\mathsf {SADS}$
are equivalent over
 $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
. -
(4)
 $\mathsf {RSpo}_2$
,
$\mathsf {RSpo}_2$
,
 $\mathsf {RSpo}^{\mathsf {CD}}_2$
, and
$\mathsf {RSpo}^{\mathsf {CD}}_2$
, and
 $\mathsf {SADS}$
are pairwise equivalent over
$\mathsf {SADS}$
are pairwise equivalent over
 $\mathsf {WKL}_0$
.
$\mathsf {WKL}_0$
. -
(5)
 $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
,
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
,
 $(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2$
, and
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2$
, and
 $\mathsf {ADS}$
are pairwise equivalent over
$\mathsf {ADS}$
are pairwise equivalent over
 $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2}$
.
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2}$
.
Proof Item (1) is by Theorem 5.5, Lemmas 6.1 and 6.3, and the fact that
![]() $\mathsf {RSpo}_{<\infty }$
implies
$\mathsf {RSpo}_{<\infty }$
implies
![]() $\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
. Item (2) is by Theorem 5.6, Lemma 6.1, and the fact that
$\mathsf {RSpo}^{\mathsf {CD}}_{<\infty }$
. Item (2) is by Theorem 5.6, Lemma 6.1, and the fact that
![]() $\mathsf {RSpo}_k$
implies
$\mathsf {RSpo}_k$
implies
![]() $\mathsf {RSpo}^{\mathsf {CD}}_k$
. Item (3) is by Theorem 5.9 and Lemma 6.2. Item (4) is by item (3) and the fact that
$\mathsf {RSpo}^{\mathsf {CD}}_k$
. Item (3) is by Theorem 5.9 and Lemma 6.2. Item (4) is by item (3) and the fact that
![]() $\mathsf {WKL}_0$
proves the equivalence of
$\mathsf {WKL}_0$
proves the equivalence of
![]() $\mathsf {RSpo}_2$
and
$\mathsf {RSpo}_2$
and
![]() $\mathsf {RSpo}^{\mathsf {CD}}_2$
, as explained in Section 3. Item (5) is by Theorem 5.11 and Lemma 6.4
$\mathsf {RSpo}^{\mathsf {CD}}_2$
, as explained in Section 3. Item (5) is by Theorem 5.11 and Lemma 6.4
We end this section with a few questions. First, we still know no better proof of
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
than the proof in
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
than the proof in
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
from Theorem 4.10. Of course,
$\Pi ^1_1\text {-}\mathsf {CA}_0$
from Theorem 4.10. Of course,
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
cannot be equivalent to
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
cannot be equivalent to
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
over
$\Pi ^1_1\text {-}\mathsf {CA}_0$
over
![]() $\mathsf {RCA}_0$
because it is a true
$\mathsf {RCA}_0$
because it is a true
![]() $\Pi ^1_2$
sentence, and true
$\Pi ^1_2$
sentence, and true
![]() $\Pi ^1_2$
sentences cannot imply
$\Pi ^1_2$
sentences cannot imply
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
over
$\Pi ^1_1\text {-}\mathsf {CA}_0$
over
![]() $\mathsf {RCA}_0$
(see [Reference Aharoni, Magidor and Shore1, Proposition 4.17]).
$\mathsf {RCA}_0$
(see [Reference Aharoni, Magidor and Shore1, Proposition 4.17]).
Question 6.7. What is the strength of
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
? What is the strength of
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
? What is the strength of
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
for each fixed
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_k$
for each fixed
![]() $k \geq 3$
?
$k \geq 3$
?
In the case
![]() $k=2$
, we do not know if
$k=2$
, we do not know if
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2}$
can be weakened to
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^0_{2}$
can be weakened to
![]() $\mathsf {RCA}_0$
in Theorem 6.6 item (5).
$\mathsf {RCA}_0$
in Theorem 6.6 item (5).
Question 6.8. Are
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
,
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_2$
,
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2$
, and
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}^{\mathsf {CD}}_2$
, and
![]() $\mathsf {ADS}$
also pairwise equivalent over
$\mathsf {ADS}$
also pairwise equivalent over
![]() $\mathsf {RCA}_0$
?
$\mathsf {RCA}_0$
?
Finally, we do not know if the equivalence of
![]() $\mathsf {RSpo}_2$
and
$\mathsf {RSpo}_2$
and
![]() $\mathsf {SADS}$
over
$\mathsf {SADS}$
over
![]() $\mathsf {WKL}_0$
of Theorem 6.6 item (4) also holds over
$\mathsf {WKL}_0$
of Theorem 6.6 item (4) also holds over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Question 6.9. What is the strength of
![]() $\mathsf {RSpo}_2$
relative to
$\mathsf {RSpo}_2$
relative to
![]() $\mathsf {RCA}_0$
? In particular, does
$\mathsf {RCA}_0$
? In particular, does
![]() $\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {RSpo}_2$
?
$\mathsf {RCA}_0 + \mathsf {SADS} \vdash \mathsf {RSpo}_2$
?
7 Extending the Rival–Sands theorem to partial orders without infinite antichains
It is possible for a partial order to have arbitrarily large finite antichains (and hence to not have finite width) but still have no infinite antichain. The goal of this section is to extend
![]() $\mathsf {RSpo}$
and
$\mathsf {RSpo}$
and
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}$
to countably infinite partial orders that do not have infinite antichains. To the best of our knowledge, these extensions are new combinatorial results. Furthermore, we show that the extension of
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}$
to countably infinite partial orders that do not have infinite antichains. To the best of our knowledge, these extensions are new combinatorial results. Furthermore, we show that the extension of
![]() $\mathsf {RSpo}$
to countably infinite partial orders without infinite antichains is equivalent to
$\mathsf {RSpo}$
to countably infinite partial orders without infinite antichains is equivalent to
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Unions of ideals play the role of unions of chains when working with partial orders without infinite antichains. Recall that an ideal in a partial order
![]() $(P, <_P)$
is a set
$(P, <_P)$
is a set
![]() $I \subseteq P$
that is downward-closed:
$I \subseteq P$
that is downward-closed:
![]() $\forall p, q \in P \; ((p \in I \;\wedge \; q \leq _P p) \;\rightarrow \; q \in I)$
and upward-directed:
$\forall p, q \in P \; ((p \in I \;\wedge \; q \leq _P p) \;\rightarrow \; q \in I)$
and upward-directed:
![]() $\forall p, q \in I \; \exists r \in I \; (p \leq _P r \;\wedge \; q \leq _P r)$
.
$\forall p, q \in I \; \exists r \in I \; (p \leq _P r \;\wedge \; q \leq _P r)$
.
A theorem of Bonnet [Reference Bonnet2, Lemma 2] states that a partial order has no infinite antichain if and only if every initial interval (i.e., downward-closed set) is a finite union of ideals. Frittaion and Marcone determined that this theorem is equivalent to
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Theorem 7.1 [Reference Frittaion and Marcone13, Theorem 4.5].
The following are equivalent over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
-
(1)
 $\mathsf {ACA}_0$
.
$\mathsf {ACA}_0$
. -
(2) For every partial order
 $(P, <_P)$
, if P has no infinite antichain, then every initial interval of P is a finite union of ideals.
$(P, <_P)$
, if P has no infinite antichain, then every initial interval of P is a finite union of ideals.
Furthermore, Frittaion and Marcone observe that in Theorem 7.1 item (2), it may additionally be assumed that the partial order
![]() $(P, <_P)$
is an essential union of finitely many ideals. This means that
$(P, <_P)$
is an essential union of finitely many ideals. This means that
![]() $P = \bigcup _{i<k}I_i$
for ideals
$P = \bigcup _{i<k}I_i$
for ideals
![]() $I_i \subseteq P$
with
$I_i \subseteq P$
with
![]() $i < k$
for some k, where additionally
$i < k$
for some k, where additionally
![]() $I_i \nsubseteq \bigcup _{\substack {j < k \\ j \neq i}}I_j$
for every
$I_i \nsubseteq \bigcup _{\substack {j < k \\ j \neq i}}I_j$
for every
![]() $i < k$
(see [Reference Frittaion and Marcone13, Lemma 3.3]). We warn the reader that when we write a partial order as a union of ideals, we may not necessarily assume that the ideals are disjoint as we do with chain decompositions.
$i < k$
(see [Reference Frittaion and Marcone13, Lemma 3.3]). We warn the reader that when we write a partial order as a union of ideals, we may not necessarily assume that the ideals are disjoint as we do with chain decompositions.
Theorem 7.2.
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
proves the statement “Every infinite partial order with no infinite antichain has a
$\Pi ^1_1\text {-}\mathsf {CA}_0$
proves the statement “Every infinite partial order with no infinite antichain has a
![]() $(0,\mathrm {cof})$
-homogeneous chain.”
$(0,\mathrm {cof})$
-homogeneous chain.”
Proof Let
![]() $(P, <_P)$
be an infinite partial order that does not have infinite antichains. Then P must have an infinite chain by
$(P, <_P)$
be an infinite partial order that does not have infinite antichains. Then P must have an infinite chain by
![]() $\mathsf {CAC}$
, which must have either an infinite ascending sequence or an infinite descending sequence by
$\mathsf {CAC}$
, which must have either an infinite ascending sequence or an infinite descending sequence by
![]() $\mathsf {ADS}$
. Thus we may assume that P contains an infinite ascending sequence A by reversing the partial order if necessary. Use
$\mathsf {ADS}$
. Thus we may assume that P contains an infinite ascending sequence A by reversing the partial order if necessary. Use
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
(and the fact that the
$\Pi ^1_1\text {-}\mathsf {CA}_0$
(and the fact that the
![]() $\Sigma ^1_1$
sets are the complements of the
$\Sigma ^1_1$
sets are the complements of the
![]() $\Pi ^1_1$
sets) to define the set
$\Pi ^1_1$
sets) to define the set
![]() $Q = \{q \in P : q{\uparrow } \text { is reverse ill-founded}\}$
of elements of P that have infinite ascending sequences above them. Notice that Q is non-empty because
$Q = \{q \in P : q{\uparrow } \text { is reverse ill-founded}\}$
of elements of P that have infinite ascending sequences above them. Notice that Q is non-empty because
![]() $A \subseteq Q$
.
$A \subseteq Q$
.
The proof proceeds in
![]() $\mathsf {ACA}_0$
from this point onward. The partial order
$\mathsf {ACA}_0$
from this point onward. The partial order
![]() $(Q, <_P)$
has no infinite antichain because it is a suborder of P. Therefore Q is an essential union of finitely many ideals
$(Q, <_P)$
has no infinite antichain because it is a suborder of P. Therefore Q is an essential union of finitely many ideals
![]() $Q = \bigcup _{i < k} I_i$
for some
$Q = \bigcup _{i < k} I_i$
for some
![]() $k> 0$
by the (1)
$k> 0$
by the (1)
![]() $\Rightarrow $
(2) direction of Theorem 7.1 and the comment that follows it. No ideal
$\Rightarrow $
(2) direction of Theorem 7.1 and the comment that follows it. No ideal
![]() $I_i$
for
$I_i$
for
![]() $i < k$
has a maximum element. Suppose for a contradiction that
$i < k$
has a maximum element. Suppose for a contradiction that
![]() $I_i$
has maximum element q. As
$I_i$
has maximum element q. As
![]() $q \in Q$
, there is an infinite ascending sequence
$q \in Q$
, there is an infinite ascending sequence
![]() $q <_P b_0 <_P b_1 <_P \cdots $
in P and therefore in Q. The element
$q <_P b_0 <_P b_1 <_P \cdots $
in P and therefore in Q. The element
![]() $b_0$
is not in
$b_0$
is not in
![]() $I_i$
because q is the maximum element of
$I_i$
because q is the maximum element of
![]() $I_i$
. Thus
$I_i$
. Thus
![]() $b_0 \in I_j$
for some
$b_0 \in I_j$
for some
![]() $j < k$
,
$j < k$
,
![]() $j \neq i$
. But then
$j \neq i$
. But then
![]() $I_i \subseteq I_j$
because
$I_i \subseteq I_j$
because
![]() $b_0 \in I_j$
,
$b_0 \in I_j$
,
![]() $q <_P b_0$
,
$q <_P b_0$
,
![]() $I_j$
is downward-closed, and q is the maximum element of
$I_j$
is downward-closed, and q is the maximum element of
![]() $I_i$
. This contradicts that the union
$I_i$
. This contradicts that the union
![]() $\bigcup _{i < k} I_i$
is essential. The partial order Q is infinite, so
$\bigcup _{i < k} I_i$
is essential. The partial order Q is infinite, so
![]() $\mathsf {RT}^1_{<\infty }$
implies that ideal
$\mathsf {RT}^1_{<\infty }$
implies that ideal
![]() $I_{\ell }$
is infinite for some
$I_{\ell }$
is infinite for some
![]() $\ell < k$
. (In fact,
$\ell < k$
. (In fact,
![]() $I_i$
is infinite for every
$I_i$
is infinite for every
![]() $i < k$
because
$i < k$
because
![]() $I_i$
is non-empty and has no maximum element.) We may thus define an infinite ascending sequence
$I_i$
is non-empty and has no maximum element.) We may thus define an infinite ascending sequence
![]() $C = \langle c_n : n \in \mathbb {N} \rangle $
that is cofinal in
$C = \langle c_n : n \in \mathbb {N} \rangle $
that is cofinal in
![]() $I_{\ell }$
as follows. Let
$I_{\ell }$
as follows. Let
![]() $\langle x_n : n \in \mathbb {N} \rangle $
enumerate the elements of
$\langle x_n : n \in \mathbb {N} \rangle $
enumerate the elements of
![]() $I_{\ell }$
. Let
$I_{\ell }$
. Let
![]() $c_0 = x_0$
, and for each n, let
$c_0 = x_0$
, and for each n, let
![]() $c_{n+1}$
be the
$c_{n+1}$
be the
![]() $<_{\mathbb {N}}$
-least element of
$<_{\mathbb {N}}$
-least element of
![]() $I_{\ell }$
with
$I_{\ell }$
with
![]() $c_{n+1}>_P c_n$
and
$c_{n+1}>_P c_n$
and
![]() $c_{n+1}>_P x_{n+1}$
. Such a
$c_{n+1}>_P x_{n+1}$
. Such a
![]() $c_{n+1}$
necessarily exists because
$c_{n+1}$
necessarily exists because
![]() $I_{\ell }$
is an ideal with no maximum element.
$I_{\ell }$
is an ideal with no maximum element.
We finish the proof by showing that some tail of C is
![]() $(0,\infty )$
-homogeneous for P and therefore is
$(0,\infty )$
-homogeneous for P and therefore is
![]() $(0,\mathrm {cof})$
-homogeneous for P. Suppose for a contradiction that no tail of C is
$(0,\mathrm {cof})$
-homogeneous for P. Suppose for a contradiction that no tail of C is
![]() $(0,\infty )$
-homogeneous. Then every tail of C has a counterexample d. For each n, let
$(0,\infty )$
-homogeneous. Then every tail of C has a counterexample d. For each n, let
![]() $d_n$
be the
$d_n$
be the
![]() $<_{\mathbb {N}}$
-least counterexample to the tail
$<_{\mathbb {N}}$
-least counterexample to the tail
![]() $C_{\geq n}$
. The partial order P has no infinite antichain, so by
$C_{\geq n}$
. The partial order P has no infinite antichain, so by
![]() $\mathsf {CAC}$
applied to the infinite suborder
$\mathsf {CAC}$
applied to the infinite suborder
![]() $\{d_n : n \in \mathbb {N}\}$
, there is a sequence
$\{d_n : n \in \mathbb {N}\}$
, there is a sequence
![]() $n_0 < n_1 < n_2 < \cdots $
such that
$n_0 < n_1 < n_2 < \cdots $
such that
![]() $\{d_{n_j} : j \in \mathbb {N}\}$
is a chain.
$\{d_{n_j} : j \in \mathbb {N}\}$
is a chain.
Arguing as in the proof of Lemma 4.8, we have that for every i, it is the case that
![]() $d_{n_i} <_P d_{n_j}$
for all sufficiently large j. Fix an i. The element
$d_{n_i} <_P d_{n_j}$
for all sufficiently large j. Fix an i. The element
![]() $d_{n_i}$
is a counterexample to
$d_{n_i}$
is a counterexample to
![]() $C_{\geq n_i}$
, so there is an
$C_{\geq n_i}$
, so there is an
![]() $s \geq n_i$
such that
$s \geq n_i$
such that
![]() $d_{n_i}>_P c_s$
and
$d_{n_i}>_P c_s$
and
![]() $d_{n_i} \mid _P C_{\geq s+1}$
. Let
$d_{n_i} \mid _P C_{\geq s+1}$
. Let
![]() $j> s+1$
, and consider
$j> s+1$
, and consider
![]() $d_{n_j}$
. The element
$d_{n_j}$
. The element
![]() $d_{n_j}$
is a counterexample to
$d_{n_j}$
is a counterexample to
![]() $C_{\geq n_j}$
, so there is a
$C_{\geq n_j}$
, so there is a
![]() $t \geq n_j$
such that
$t \geq n_j$
such that
![]() $d_{n_j}>_P c_t$
. We cannot have that
$d_{n_j}>_P c_t$
. We cannot have that
![]() $d_{n_j} \leq _P d_{n_i}$
because this would yield that
$d_{n_j} \leq _P d_{n_i}$
because this would yield that
![]() $c_{s+1} <_P c_t <_P d_{n_j} \leq _P d_{n_i}$
, contradicting that
$c_{s+1} <_P c_t <_P d_{n_j} \leq _P d_{n_i}$
, contradicting that
![]() $d_{n_i} \mid _P c_{s+1}$
. Note here that
$d_{n_i} \mid _P c_{s+1}$
. Note here that
![]() $s+1 < j \leq n_j \leq t$
, so
$s+1 < j \leq n_j \leq t$
, so
![]() $c_{s+1} < _P c_t$
because C is an ascending sequence. Therefore it must be that
$c_{s+1} < _P c_t$
because C is an ascending sequence. Therefore it must be that
![]() $d_{n_i} <_P d_{n_j}$
because we know that
$d_{n_i} <_P d_{n_j}$
because we know that
![]() $d_{n_i} \lessgtr _P d_{n_j}$
.
$d_{n_i} \lessgtr _P d_{n_j}$
.
Using the above, we may thin the sequence
![]() $n_0 < n_1 < n_2 < \cdots $
so that
$n_0 < n_1 < n_2 < \cdots $
so that
![]() ${d_{n_0} <_P d_{n_1} <_P d_{n_2} <_P \cdots }$
is an infinite ascending sequence in P. It follows that
${d_{n_0} <_P d_{n_1} <_P d_{n_2} <_P \cdots }$
is an infinite ascending sequence in P. It follows that
![]() $\{d_{n_j} : j \in \mathbb {N}\} \subseteq Q$
. By
$\{d_{n_j} : j \in \mathbb {N}\} \subseteq Q$
. By
![]() $\mathsf {RT}^1_{<\infty }$
, there is an
$\mathsf {RT}^1_{<\infty }$
, there is an
![]() $s < k$
such that
$s < k$
such that
![]() $I_s$
contains
$I_s$
contains
![]() $d_{n_j}$
for infinitely many j. We may therefore further thin the sequence
$d_{n_j}$
for infinitely many j. We may therefore further thin the sequence
![]() $n_0 < n_1 < n_2 < \cdots $
so that
$n_0 < n_1 < n_2 < \cdots $
so that
![]() $\{d_{n_j} : j \in \mathbb {N}\} \subseteq I_s$
. We cannot have that
$\{d_{n_j} : j \in \mathbb {N}\} \subseteq I_s$
. We cannot have that
![]() $s = \ell $
because every element of
$s = \ell $
because every element of
![]() $I_{\ell }$
is below a tail of C by the construction of C, whereas
$I_{\ell }$
is below a tail of C by the construction of C, whereas
![]() $d_{n_j}$
is incomparable with a tail of C for every j. Finally, we see that
$d_{n_j}$
is incomparable with a tail of C for every j. Finally, we see that
![]() $I_{\ell } \leq _{\forall \exists } C$
by the construction of C and that
$I_{\ell } \leq _{\forall \exists } C$
by the construction of C and that
![]() $C \leq _{\forall \exists } \{d_{n_j} : j \in \mathbb {N}\}$
because
$C \leq _{\forall \exists } \{d_{n_j} : j \in \mathbb {N}\}$
because
![]() $c_{n_j} <_P d_{n_j}$
for every j. Therefore
$c_{n_j} <_P d_{n_j}$
for every j. Therefore
![]() $I_{\ell } \leq _{\forall \exists } \{d_{n_j} : j \in \mathbb {N}\} \subseteq I_s$
, so
$I_{\ell } \leq _{\forall \exists } \{d_{n_j} : j \in \mathbb {N}\} \subseteq I_s$
, so
![]() $I_{\ell } \subseteq I_s$
because
$I_{\ell } \subseteq I_s$
because
![]() $I_s$
is an ideal. This contradicts that the union
$I_s$
is an ideal. This contradicts that the union
![]() $\bigcup _{i < k} I_i$
is essential because
$\bigcup _{i < k} I_i$
is essential because
![]() $s \neq \ell $
.
$s \neq \ell $
.
As in the case of
![]() $\mathsf {RSpo}_{<\infty }$
versus
$\mathsf {RSpo}_{<\infty }$
versus
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
, if we only want to produce a chain that is
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
, if we only want to produce a chain that is
![]() $(0,\infty )$
-homogeneous rather than
$(0,\infty )$
-homogeneous rather than
![]() $(0,\mathrm {cof})$
-homogeneous in an infinite partial order
$(0,\mathrm {cof})$
-homogeneous in an infinite partial order
![]() $(P, <_P)$
with no infinite antichain, then we may split into the cases of where P contains a suborder of type
$(P, <_P)$
with no infinite antichain, then we may split into the cases of where P contains a suborder of type
![]() $\zeta $
and where it does not.
$\zeta $
and where it does not.
Theorem 7.3.
![]() $\mathsf {ACA}_0$
proves the statement “Every infinite partial order with no infinite antichain has a
$\mathsf {ACA}_0$
proves the statement “Every infinite partial order with no infinite antichain has a
![]() $(0,\infty )$
-homogeneous chain.”
$(0,\infty )$
-homogeneous chain.”
Proof The proof is the same as the proof of Theorem 7.2, except now we use Lemma 4.5 item (2) in place of
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
. Let
$\Pi ^1_1\text {-}\mathsf {CA}_0$
. Let
![]() $(P, <_P)$
be an infinite partial order that does not have infinite antichains. A chain of order-type
$(P, <_P)$
be an infinite partial order that does not have infinite antichains. A chain of order-type
![]() $\zeta $
is necessarily
$\zeta $
is necessarily
![]() $(0,\infty )$
-homogeneous, so we may additionally assume that P has no suborder of type
$(0,\infty )$
-homogeneous, so we may additionally assume that P has no suborder of type
![]() $\zeta $
. As in the proof of Theorem 7.2, we may assume that P has an infinite ascending sequence by applying
$\zeta $
. As in the proof of Theorem 7.2, we may assume that P has an infinite ascending sequence by applying
![]() $\mathsf {CAC}$
and
$\mathsf {CAC}$
and
![]() $\mathsf {ADS}$
and by reversing the order if needed. By the (1)
$\mathsf {ADS}$
and by reversing the order if needed. By the (1)
![]() $\Rightarrow $
(2) direction of Lemma 4.5 and the comments that follow it, we may form the set
$\Rightarrow $
(2) direction of Lemma 4.5 and the comments that follow it, we may form the set
![]() $Q = \{q \in P : q{\uparrow } \text { is reverse ill-founded}\}$
. The proof now continues exactly as in that of Theorem 7.2.
$Q = \{q \in P : q{\uparrow } \text { is reverse ill-founded}\}$
. The proof now continues exactly as in that of Theorem 7.2.
Recall that a partial order
![]() $(P, <_P)$
is a well-partial-order if for every function
$(P, <_P)$
is a well-partial-order if for every function
![]() $h \colon \mathbb {N} \rightarrow P$
, there are
$h \colon \mathbb {N} \rightarrow P$
, there are
![]() $m, n \in \mathbb {N}$
with
$m, n \in \mathbb {N}$
with
![]() $m < n$
such that
$m < n$
such that
![]() $f(m) \leq _P f(n)$
. A function
$f(m) \leq _P f(n)$
. A function
![]() $h \colon \mathbb {N} \rightarrow P$
witnessing that P is not a well-partial-order (i.e., such that
$h \colon \mathbb {N} \rightarrow P$
witnessing that P is not a well-partial-order (i.e., such that
![]() $h(m) \nleq _P h(n)$
whenever
$h(m) \nleq _P h(n)$
whenever
![]() $m < n$
) is called a bad sequence. Any bijective enumeration of an infinite antichain in a partial order
$m < n$
) is called a bad sequence. Any bijective enumeration of an infinite antichain in a partial order
![]() $(P, <_P)$
is a bad sequence, so well-partial-orders do not have infinite antichains.
$(P, <_P)$
is a bad sequence, so well-partial-orders do not have infinite antichains.
To reverse Theorem 7.3 for well-partial-orders, we employ the construction of [Reference Frittaion, Hendtlass, Marcone, Shafer and Van der Meeren12, Definition 4.2], which is a generalization of Construction 4.4. This construction takes an injection
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
and a finite partial order P with a distinguished element
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
and a finite partial order P with a distinguished element
![]() $x \in P$
and produces an infinite partial order
$x \in P$
and produces an infinite partial order
![]() $\Xi _f(P,x)$
such that the range of f is recursive in the join of f with any bad sequence in
$\Xi _f(P,x)$
such that the range of f is recursive in the join of f with any bad sequence in
![]() $\Xi _f(P,x)$
. That is, either
$\Xi _f(P,x)$
. That is, either
![]() $\Xi _f(P,x)$
is a well-partial-order or the range of f exists as a set. Thus given an injection f, the strategy is to construct
$\Xi _f(P,x)$
is a well-partial-order or the range of f exists as a set. Thus given an injection f, the strategy is to construct
![]() $\Xi _f(P,x)$
for the
$\Xi _f(P,x)$
for the
![]() $2$
-element antichain
$2$
-element antichain
![]() $P = \{x, y\}$
, show that
$P = \{x, y\}$
, show that
![]() $\Xi _f(P,x)$
has no
$\Xi _f(P,x)$
has no
![]() $(0,\infty )$
-homogeneous chain, conclude that
$(0,\infty )$
-homogeneous chain, conclude that
![]() $\Xi _f(P,x)$
is not a well-partial-order, and then conclude that the range of f exists as a set.
$\Xi _f(P,x)$
is not a well-partial-order, and then conclude that the range of f exists as a set.
We include Construction 7.4 for the reader’s convenience. Given an injection
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
, let
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
, let
 $$ \begin{align*} T_s &= \{n < s : n \text{ is true at stage } s\}\\ &= \{n < s : \forall k \, (n < k \leq s \;\rightarrow\; f(n) < f(k))\}, \end{align*} $$
$$ \begin{align*} T_s &= \{n < s : n \text{ is true at stage } s\}\\ &= \{n < s : \forall k \, (n < k \leq s \;\rightarrow\; f(n) < f(k))\}, \end{align*} $$
for each
![]() $s \in \mathbb {N}$
.
$s \in \mathbb {N}$
.
Construction 7.4 [Reference Frittaion, Hendtlass, Marcone, Shafer and Van der Meeren12, Definition 4.2].
Let
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection, let
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection, let
![]() $(P, <_P)$
be a finite partial order, and let
$(P, <_P)$
be a finite partial order, and let
![]() $x \in P$
. Define the partial order
$x \in P$
. Define the partial order
![]() $(Q, <_Q) = \Xi _f(P,x)$
as follows. Make countably many disjoint copies
$(Q, <_Q) = \Xi _f(P,x)$
as follows. Make countably many disjoint copies
![]() $(P_n, <_{P_n})$
of P by setting
$(P_n, <_{P_n})$
of P by setting
![]() $P_n = \{n\} \times P$
and by setting
$P_n = \{n\} \times P$
and by setting
![]() $\langle n, y \rangle <_{P_n} \langle n, z \rangle $
if and only if
$\langle n, y \rangle <_{P_n} \langle n, z \rangle $
if and only if
![]() $y <_P z$
for all
$y <_P z$
for all
![]() $n \in \mathbb {N}$
and all
$n \in \mathbb {N}$
and all
![]() $y, z \in P$
. Let
$y, z \in P$
. Let
![]() $x_n = \langle n, x \rangle $
denote the copy of x in
$x_n = \langle n, x \rangle $
denote the copy of x in
![]() $P_n$
. The domain of Q is
$P_n$
. The domain of Q is
![]() $\bigcup _{n \in \mathbb {N}}P_n$
. Define
$\bigcup _{n \in \mathbb {N}}P_n$
. Define
![]() $<_Q$
in stages, where at stage s,
$<_Q$
in stages, where at stage s,
![]() $<_Q$
is defined on
$<_Q$
is defined on
![]() $\bigcup _{n \leq s}P_n$
.
$\bigcup _{n \leq s}P_n$
.
-
• At stage
 $0$
, define
$0$
, define
 $<_Q$
to be
$<_Q$
to be
 $<_{P_0}$
on
$<_{P_0}$
on
 $P_0$
.
$P_0$
. -
• Suppose
 $<_Q$
is defined on
$<_Q$
is defined on
 $\bigcup _{n \leq s} P_s$
. There are two cases.
$\bigcup _{n \leq s} P_s$
. There are two cases.-
(1) If
 $T_{s+1} \subsetneq T_s \cup \{s\}$
, let
$T_{s+1} \subsetneq T_s \cup \{s\}$
, let
 $n_0$
be the least element of
$n_0$
be the least element of
 $(T_s \cup \{s\}) \setminus T_{s+1}$
, and place
$(T_s \cup \{s\}) \setminus T_{s+1}$
, and place
 $P_{s+1}$
immediately above
$P_{s+1}$
immediately above
 $x_{n_0}$
. That is, place the elements of
$x_{n_0}$
. That is, place the elements of
 $P_{s+1}$
above all
$P_{s+1}$
above all
 $y \in \bigcup _{n \leq s} P_s$
such that
$y \in \bigcup _{n \leq s} P_s$
such that
 $y \leq _Q x_{n_0}$
, below all
$y \leq _Q x_{n_0}$
, below all
 $y \in \bigcup _{n \leq s} P_s$
such that
$y \in \bigcup _{n \leq s} P_s$
such that
 $y>_Q x_{n_0}$
, and incomparable with all
$y>_Q x_{n_0}$
, and incomparable with all
 $y \in \bigcup _{n \leq s} P_s$
that are incomparable with
$y \in \bigcup _{n \leq s} P_s$
that are incomparable with
 $x_{n_0}$
.
$x_{n_0}$
. -
(2) If
 $T_{s+1} = T_s \cup \{s\}$
, place
$T_{s+1} = T_s \cup \{s\}$
, place
 $P_{s+1}$
immediately below
$P_{s+1}$
immediately below
 $x_s$
. That is, place the elements of
$x_s$
. That is, place the elements of
 $P_{s+1}$
above all
$P_{s+1}$
above all
 $y \in \bigcup _{n \leq s} P_s$
such that
$y \in \bigcup _{n \leq s} P_s$
such that
 $y <_Q x_s$
, below all
$y <_Q x_s$
, below all
 $y \in \bigcup _{n \leq s} P_s$
such that
$y \in \bigcup _{n \leq s} P_s$
such that
 $y \geq _Q x_s$
, and incomparable with all
$y \geq _Q x_s$
, and incomparable with all
 $y \in \bigcup _{n \leq s} P_s$
that are incomparable with
$y \in \bigcup _{n \leq s} P_s$
that are incomparable with
 $x_s$
.
$x_s$
.
In both cases, define
 $<_Q$
to be
$<_Q$
to be
 $<_{P_{s+1}}$
on
$<_{P_{s+1}}$
on
 $P_{s+1}$
.
$P_{s+1}$
. -
This construction can be carried out in
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
The following two lemmas encapsulate the important properties of Construction 7.4.
Lemma 7.5 [Reference Frittaion, Hendtlass, Marcone, Shafer and Van der Meeren12, Lemma 4.3].
The following is provable in
![]() $\mathsf {RCA}_0$
. Let
$\mathsf {RCA}_0$
. Let
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection, let P be a finite partial order, let
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection, let P be a finite partial order, let
![]() $x \in P$
, and let
$x \in P$
, and let
![]() $(Q, <_Q) = \Xi _f (P,x)$
. Consider
$(Q, <_Q) = \Xi _f (P,x)$
. Consider
![]() $m, n \in \mathbb {N}$
with
$m, n \in \mathbb {N}$
with
![]() $n < m$
.
$n < m$
.
-
(1) If
 $n \in T_m$
, then
$n \in T_m$
, then
 $P_m <_Q x_n$
and
$P_m <_Q x_n$
and
 $\forall y \in P_n \; (x_n \mid _Q y \;\rightarrow \; P_m \mid _Q y)$
.
$\forall y \in P_n \; (x_n \mid _Q y \;\rightarrow \; P_m \mid _Q y)$
. -
(2) If
 $n \notin T_m$
, then
$n \notin T_m$
, then
 $x_n <_Q P_m$
.
$x_n <_Q P_m$
.
Lemma 7.6 [Reference Frittaion, Hendtlass, Marcone, Shafer and Van der Meeren12, Lemma 4.4].
The following is provable in
![]() $\mathsf {RCA}_0$
. Let
$\mathsf {RCA}_0$
. Let
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection, let P be a finite partial order, let
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection, let P be a finite partial order, let
![]() $x \in P$
, and let
$x \in P$
, and let
![]() $(Q, <_Q) = \Xi _f (P,x)$
. If Q is not a well-partial-order, then the range of f exists as a set.
$(Q, <_Q) = \Xi _f (P,x)$
. If Q is not a well-partial-order, then the range of f exists as a set.
We now give the reversal for Theorem 7.3.
Lemma 7.7. The statement “Every infinite well-partial-order has a
![]() $(0,\infty )$
-homogeneous chain” implies
$(0,\infty )$
-homogeneous chain” implies
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Proof Let
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection. Let
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection. Let
![]() $(P, <_P)$
be the
$(P, <_P)$
be the
![]() $2$
-element partial order
$2$
-element partial order
![]() $P = \{x, y\}$
with
$P = \{x, y\}$
with
![]() $x \mid _P y$
. Let
$x \mid _P y$
. Let
![]() $(Q, <_Q) = \Xi _f(P, x)$
, and recall that
$(Q, <_Q) = \Xi _f(P, x)$
, and recall that
![]() $Q = \bigcup _{n \in \mathbb {N}}P_n$
, where
$Q = \bigcup _{n \in \mathbb {N}}P_n$
, where
![]() $P_n = \{n\} \times P$
for each n. Let
$P_n = \{n\} \times P$
for each n. Let
![]() $x_n = \langle n, x \rangle $
and
$x_n = \langle n, x \rangle $
and
![]() $y_n = \langle n, y \rangle $
denote the copies of x and y in
$y_n = \langle n, y \rangle $
denote the copies of x and y in
![]() $P_n$
for each n.
$P_n$
for each n.
First, assume that there is an infinite set
![]() $C \subseteq Q$
consisting only of elements
$C \subseteq Q$
consisting only of elements
![]() $y_n$
for false numbers n, and furthermore assume that there are no false numbers n and k with
$y_n$
for false numbers n, and furthermore assume that there are no false numbers n and k with
![]() $y_n \in C$
and
$y_n \in C$
and
![]() $y_n <_Q x_k$
. Then the number k is true whenever there is an n such that
$y_n <_Q x_k$
. Then the number k is true whenever there is an n such that
![]() $y_n \in C$
and
$y_n \in C$
and
![]() $y_n <_Q x_k$
. Moreover, if k is a true number, then there is an
$y_n <_Q x_k$
. Moreover, if k is a true number, then there is an
![]() $m> k$
with
$m> k$
with
![]() $y_m \in C$
because C is infinite, and we have that
$y_m \in C$
because C is infinite, and we have that
![]() $y_m <_Q x_k$
by Lemma 7.5 item (1). Thus the true numbers k are
$y_m <_Q x_k$
by Lemma 7.5 item (1). Thus the true numbers k are
![]() $\Sigma ^0_1$
-definable by the formula
$\Sigma ^0_1$
-definable by the formula
![]() $\exists m \, (y_m \in C \;\wedge \; y_m <_Q x_k)$
. The original definition of the true numbers from Definition 4.3 is
$\exists m \, (y_m \in C \;\wedge \; y_m <_Q x_k)$
. The original definition of the true numbers from Definition 4.3 is
![]() $\Pi ^0_1$
, so the set of true numbers exists by
$\Pi ^0_1$
, so the set of true numbers exists by
![]() $\Delta ^0_1$
comprehension. Thus the range of f exists as a set.
$\Delta ^0_1$
comprehension. Thus the range of f exists as a set.
Second, assume instead that whenever
![]() $C \subseteq Q$
is an infinite set consisting only of elements
$C \subseteq Q$
is an infinite set consisting only of elements
![]() $y_n$
for false numbers n, there are false numbers n and k with
$y_n$
for false numbers n, there are false numbers n and k with
![]() $y_n \in C$
and
$y_n \in C$
and
![]() $y_n <_Q x_k$
. The goal of this case is to show that Q has no
$y_n <_Q x_k$
. The goal of this case is to show that Q has no
![]() $(0,\infty )$
-homogeneous chain. The hypothesis “Every infinite well-partial-order has a
$(0,\infty )$
-homogeneous chain. The hypothesis “Every infinite well-partial-order has a
![]() $(0,\infty )$
-homogeneous chain” then implies that Q is not a well-partial-order, so the range of f exists as a set by Lemma 7.6.
$(0,\infty )$
-homogeneous chain” then implies that Q is not a well-partial-order, so the range of f exists as a set by Lemma 7.6.
Consider an infinite chain
![]() $C \subseteq Q$
. We show that C is not
$C \subseteq Q$
. We show that C is not
![]() $(0,\infty )$
-homogeneous. Observe that if n is a true number, then
$(0,\infty )$
-homogeneous. Observe that if n is a true number, then
![]() $n \in T_m$
for all
$n \in T_m$
for all
![]() $m> n$
and therefore that
$m> n$
and therefore that
![]() $y_n \mid _P P_m$
for all
$y_n \mid _P P_m$
for all
![]() $m> n$
by Lemma 7.5 item (1). There are now three sub-cases.
$m> n$
by Lemma 7.5 item (1). There are now three sub-cases.
-
• There is a number n with
 $x_n \in C$
. Let m be a true number with
$x_n \in C$
. Let m be a true number with
 $m> n$
. Then
$m> n$
. Then
 $y_m \lessgtr _Q x_n$
by Lemma 7.5, but
$y_m \lessgtr _Q x_n$
by Lemma 7.5, but
 $y_m$
is only comparable with finitely many elements of Q because m is true. So
$y_m$
is only comparable with finitely many elements of Q because m is true. So
 $y_m$
witnesses that C is not
$y_m$
witnesses that C is not
 $(0,\infty )$
-homogeneous.
$(0,\infty )$
-homogeneous. -
• There is a true number n with
 $y_n \in C$
. Then
$y_n \in C$
. Then
 $y_n$
is comparable with only finitely many elements of Q, so C cannot be an infinite chain.
$y_n$
is comparable with only finitely many elements of Q, so C cannot be an infinite chain. -
• The chain C consists only of elements
 $y_n$
for false numbers n. Then by the case assumption there are false numbers n and k with
$y_n$
for false numbers n. Then by the case assumption there are false numbers n and k with
 $y_n \in C$
and
$y_n \in C$
and
 $y_n <_Q x_k$
. Let
$y_n <_Q x_k$
. Let
 $m> k$
be such that m is true and that
$m> k$
be such that m is true and that
 $k \notin T_m$
. Then
$k \notin T_m$
. Then
 $y_n <_Q x_k <_Q y_m$
by Lemma 7.5 item (2), but
$y_n <_Q x_k <_Q y_m$
by Lemma 7.5 item (2), but
 $y_m$
is only comparable with finitely many elements of Q because m is true. So
$y_m$
is only comparable with finitely many elements of Q because m is true. So
 $y_m$
witnesses that C is not
$y_m$
witnesses that C is not
 $(0,\infty )$
-homogeneous.
$(0,\infty )$
-homogeneous.
We have shown that the range of f exists as a set in both of the main cases. We may therefore conclude that
![]() $\mathsf {ACA}_0$
holds by Lemma 2.1.
$\mathsf {ACA}_0$
holds by Lemma 2.1.
Theorem 7.8. The following are equivalent over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
-
(1)
 $\mathsf {ACA}_0$
.
$\mathsf {ACA}_0$
. -
(2) Every infinite partial order with no infinite antichain has a
 $(0,\infty )$
-homogeneous chain.
$(0,\infty )$
-homogeneous chain. -
(3) Every infinite well-partial-order has a
 $(0,\infty )$
-homogeneous chain.
$(0,\infty )$
-homogeneous chain.
Proof We have that (1)
![]() $\Rightarrow $
(2) by Theorem 7.3, that (2)
$\Rightarrow $
(2) by Theorem 7.3, that (2)
![]() $\Rightarrow $
(3) because well-partial-orders do not have infinite antichains, and that (3)
$\Rightarrow $
(3) because well-partial-orders do not have infinite antichains, and that (3)
![]() $\Rightarrow $
(1) by Lemma 7.7.
$\Rightarrow $
(1) by Lemma 7.7.
It follows that the statement “Every infinite partial order with no infinite antichain has a
![]() $(0,\mathrm {cof})$
-homogeneous chain” implies
$(0,\mathrm {cof})$
-homogeneous chain” implies
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
. As with
$\mathsf {RCA}_0$
. As with
![]() $(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
, we know no better upper bound for the statement than
$(0,\mathrm {cof})\text {-}\mathsf {RSpo}_{<\infty }$
, we know no better upper bound for the statement than
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
, yet the statement cannot be equivalent to
$\Pi ^1_1\text {-}\mathsf {CA}_0$
, yet the statement cannot be equivalent to
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
over
$\Pi ^1_1\text {-}\mathsf {CA}_0$
over
![]() $\mathsf {RCA}_0$
because it is
$\mathsf {RCA}_0$
because it is
![]() $\Pi ^1_2$
.
$\Pi ^1_2$
.
Question 7.9. What is the strength of the statement “Every infinite partial order with no infinite antichain has a
![]() $(0,\mathrm {cof})$
-homogeneous chain” relative to
$(0,\mathrm {cof})$
-homogeneous chain” relative to
![]() $\mathsf {RCA}_0$
?
$\mathsf {RCA}_0$
?
8 Maximal chain principles and comments on the original Rival–Sands proof
The original proof of
![]() $\mathsf {RSpo}_{<\infty }$
given by Rival and Sands in [Reference Rival and Sands28] relies on the following maximality principle, which we name
$\mathsf {RSpo}_{<\infty }$
given by Rival and Sands in [Reference Rival and Sands28] relies on the following maximality principle, which we name
![]() $\mathsf {MMLC}$
for the maximal max-less chain principle.
$\mathsf {MMLC}$
for the maximal max-less chain principle.
Definition 8.1. Call a chain C in a partial order
![]() $(P, <_P)$
max-less if C has no maximum element:
$(P, <_P)$
max-less if C has no maximum element:
![]() $\forall x \in C \; \exists y \in C \; (x <_P y)$
. The maximal max-less chain principle (
$\forall x \in C \; \exists y \in C \; (x <_P y)$
. The maximal max-less chain principle (
![]() $\mathsf {MMLC}$
) is the following statement. For every partial order
$\mathsf {MMLC}$
) is the following statement. For every partial order
![]() $(P, <_P)$
, there is a max-less chain that is
$(P, <_P)$
, there is a max-less chain that is
![]() $\subseteq $
-maximal among the max-less chains of P. That is, there is a max-less chain
$\subseteq $
-maximal among the max-less chains of P. That is, there is a max-less chain
![]() $C \subseteq P$
for which
$C \subseteq P$
for which
![]() $C \subseteq D \subseteq P$
implies
$C \subseteq D \subseteq P$
implies
![]() $C = D$
for all max-less chains D of P. Call such a C a maximal max-less chain in P.
$C = D$
for all max-less chains D of P. Call such a C a maximal max-less chain in P.
Similarly, call a chain C in a partial order
![]() $(P, <_P)$
min-less if C has no minimum element:
$(P, <_P)$
min-less if C has no minimum element:
![]() $\forall x \in C \; \exists y \in C \; (y <_P x)$
. By reversing the partial order, we see that, over
$\forall x \in C \; \exists y \in C \; (y <_P x)$
. By reversing the partial order, we see that, over
![]() $\mathsf {RCA}_0$
,
$\mathsf {RCA}_0$
,
![]() $\mathsf {MMLC}$
is equivalent to the statement “For every partial order
$\mathsf {MMLC}$
is equivalent to the statement “For every partial order
![]() $(P, <_P)$
, there is a min-less chain that is
$(P, <_P)$
, there is a min-less chain that is
![]() $\subseteq $
-maximal among the min-less chains of P.”
$\subseteq $
-maximal among the min-less chains of P.”
We very roughly sketch the Rival and Sands proof, using some of the terminology we have introduced here. Let
![]() $(P, <_P)$
be a countably infinite partial order of finite width k for some k. Suppose for a contradiction that
$(P, <_P)$
be a countably infinite partial order of finite width k for some k. Suppose for a contradiction that
![]() $(P, <_P)$
contains no
$(P, <_P)$
contains no
![]() $(0,\infty )$
-homogeneous chain. The partial order P contains either an infinite ascending sequence or an infinite descending sequence, and we may assume that P contains an infinite ascending sequence by reversing the order if necessary. Define a sequence
$(0,\infty )$
-homogeneous chain. The partial order P contains either an infinite ascending sequence or an infinite descending sequence, and we may assume that P contains an infinite ascending sequence by reversing the order if necessary. Define a sequence
![]() $(S_i, C_i, D_i)_{i \leq k+1}$
of triples of subsets of P as follows. First, let
$(S_i, C_i, D_i)_{i \leq k+1}$
of triples of subsets of P as follows. First, let
![]() $S_0 = P$
, by
$S_0 = P$
, by
![]() $\mathsf {MMLC}$
let
$\mathsf {MMLC}$
let
![]() $C_0$
be a maximal max-less chain in P, and let
$C_0$
be a maximal max-less chain in P, and let
![]() $D_0$
be a cofinal infinite ascending sequence in
$D_0$
be a cofinal infinite ascending sequence in
![]() $C_0$
. Given
$C_0$
. Given
![]() $(S_i, C_i, D_i)$
, let
$(S_i, C_i, D_i)$
, let
![]() $S_{i+1}$
consist of the elements of P that are counterexamples to the
$S_{i+1}$
consist of the elements of P that are counterexamples to the
![]() $(0,\infty )$
-homogeneity of
$(0,\infty )$
-homogeneity of
![]() $D_i$
in the sense of Definition 4.7. Again by
$D_i$
in the sense of Definition 4.7. Again by
![]() $\mathsf {MMLC}$
, let
$\mathsf {MMLC}$
, let
![]() $C_{i+1}$
be a maximal max-less chain in
$C_{i+1}$
be a maximal max-less chain in
![]() $S_{i+1}$
, and let
$S_{i+1}$
, and let
![]() $D_{i+1}$
be a cofinal infinite ascending sequence in
$D_{i+1}$
be a cofinal infinite ascending sequence in
![]() $C_{i+1}$
. Using the maximality of the
$C_{i+1}$
. Using the maximality of the
![]() $C_j$
’s, show that
$C_j$
’s, show that
![]() $D_i \subseteq S_j$
whenever
$D_i \subseteq S_j$
whenever
![]() $j \leq i \leq k+1$
. This property allows us to choose an antichain
$j \leq i \leq k+1$
. This property allows us to choose an antichain
![]() $\{d_0, \dots , d_k\}$
with
$\{d_0, \dots , d_k\}$
with
![]() $d_i \in D_{k+1-i}$
for each
$d_i \in D_{k+1-i}$
for each
![]() $i \leq k$
, which contradicts that P has width k. The
$i \leq k$
, which contradicts that P has width k. The
![]() $d_i$
’s are chosen back-to-front, with
$d_i$
’s are chosen back-to-front, with
![]() $d_0$
chosen from
$d_0$
chosen from
![]() $D_{k+1}$
, then
$D_{k+1}$
, then
![]() $d_1$
chosen from
$d_1$
chosen from
![]() $D_k$
, and so on. Thus this method does not suffice to prove the extensions of Theorems 7.2 and 7.3 to partial orders without infinite antichains but not necessarily of finite width.
$D_k$
, and so on. Thus this method does not suffice to prove the extensions of Theorems 7.2 and 7.3 to partial orders without infinite antichains but not necessarily of finite width.
We analyze the strength of
![]() $\mathsf {MMLC}$
and of a few other statements concerning maximal chains in partial orders. In particular, we show that
$\mathsf {MMLC}$
and of a few other statements concerning maximal chains in partial orders. In particular, we show that
![]() $\mathsf {MMLC}$
is equivalent to
$\mathsf {MMLC}$
is equivalent to
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
over
$\Pi ^1_1\text {-}\mathsf {CA}_0$
over
![]() $\mathsf {RCA}_0$
. Therefore, the original proof by Rival and Sands requires
$\mathsf {RCA}_0$
. Therefore, the original proof by Rival and Sands requires
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
in the sense that it relies on a principle that is equivalent to
$\Pi ^1_1\text {-}\mathsf {CA}_0$
in the sense that it relies on a principle that is equivalent to
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
. Furthermore, if a standard bound on the width k of the partial orders being considered is not fixed in advance, then the original Rival and Sands proof is not a proof in
$\Pi ^1_1\text {-}\mathsf {CA}_0$
. Furthermore, if a standard bound on the width k of the partial orders being considered is not fixed in advance, then the original Rival and Sands proof is not a proof in
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
because it iterates applying
$\Pi ^1_1\text {-}\mathsf {CA}_0$
because it iterates applying
![]() $\mathsf {MMLC}$
a finite-but-arbitrarily-large number of times.
$\mathsf {MMLC}$
a finite-but-arbitrarily-large number of times.
It is well-known and easy to show that
![]() $\mathsf {RCA}_0$
suffices to produce a maximal chain and a maximal antichain in a given partial order
$\mathsf {RCA}_0$
suffices to produce a maximal chain and a maximal antichain in a given partial order
![]() $(P, <_P)$
. Enumerate the elements of P as
$(P, <_P)$
. Enumerate the elements of P as
![]() $\langle p_n : n \in \mathbb {N} \rangle $
, and add element
$\langle p_n : n \in \mathbb {N} \rangle $
, and add element
![]() $p_n$
to the chain (antichain) if and only if it is comparable (incomparable) to all the elements previously added to the chain (antichain). However, if we want to extend a given chain C to a maximal chain D, then
$p_n$
to the chain (antichain) if and only if it is comparable (incomparable) to all the elements previously added to the chain (antichain). However, if we want to extend a given chain C to a maximal chain D, then
![]() $\mathsf {ACA}_0$
is required.
$\mathsf {ACA}_0$
is required.
Proposition 8.2. The following are equivalent over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
-
(1)
 $\mathsf {ACA}_0$
.
$\mathsf {ACA}_0$
. -
(2) For every partial order
 $(P, <_P)$
and chain
$(P, <_P)$
and chain
 $C \subseteq P$
, there is a maximal chain D with
$C \subseteq P$
, there is a maximal chain D with
 $C \subseteq D$
.
$C \subseteq D$
.
Proof For the forward direction, let
![]() $(P, <_P)$
be a partial order, and let
$(P, <_P)$
be a partial order, and let
![]() $C \subseteq P$
be a chain. Let
$C \subseteq P$
be a chain. Let
![]() $Q = \{q \in P : \forall c \in C \; (q \lessgtr _P c)\}$
be the set of elements of P that are comparable with all elements of C, and consider the partial order
$Q = \{q \in P : \forall c \in C \; (q \lessgtr _P c)\}$
be the set of elements of P that are comparable with all elements of C, and consider the partial order
![]() $(Q, <_P)$
. Notice that
$(Q, <_P)$
. Notice that
![]() $C \subseteq Q$
because C is a chain. Let D be a maximal chain in Q, which can be produced in
$C \subseteq Q$
because C is a chain. Let D be a maximal chain in Q, which can be produced in
![]() $\mathsf {RCA}_0$
as described above. As
$\mathsf {RCA}_0$
as described above. As
![]() $D \subseteq Q$
, every element of D is comparable with every element of C. Therefore
$D \subseteq Q$
, every element of D is comparable with every element of C. Therefore
![]() $C \subseteq D$
by the maximality of D in Q. We claim that D is also a maximal chain in P. Suppose for a contradiction that it is not. Then there is a
$C \subseteq D$
by the maximality of D in Q. We claim that D is also a maximal chain in P. Suppose for a contradiction that it is not. Then there is a
![]() $p \in P \setminus D$
that is comparable with every element of D. Then p is also comparable with every element of C, so
$p \in P \setminus D$
that is comparable with every element of D. Then p is also comparable with every element of C, so
![]() $p \in Q$
. Thus there is a
$p \in Q$
. Thus there is a
![]() $p \in Q \setminus D$
that is comparable with every element of D. This contradicts the maximality of D in Q. Therefore D is a maximal chain in P with
$p \in Q \setminus D$
that is comparable with every element of D. This contradicts the maximality of D in Q. Therefore D is a maximal chain in P with
![]() $C \subseteq D$
.
$C \subseteq D$
.
For the reversal, let
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection. We define a partial order
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
be an injection. We define a partial order
![]() $(P, <_P)$
and a chain
$(P, <_P)$
and a chain
![]() $C \subseteq P$
in such a way that the range of f can be extracted from f and any maximal chain
$C \subseteq P$
in such a way that the range of f can be extracted from f and any maximal chain
![]() $D \supseteq C$
.
$D \supseteq C$
.
Let
![]() $(L, <_L)$
be the linear order defined in Construction 4.4 for f, where
$(L, <_L)$
be the linear order defined in Construction 4.4 for f, where
![]() $L = \{\ell _n : n \in \mathbb {N}\}$
. Let
$L = \{\ell _n : n \in \mathbb {N}\}$
. Let
![]() $P = \{c_n, \ell _n : n \in \mathbb {N}\}$
, let
$P = \{c_n, \ell _n : n \in \mathbb {N}\}$
, let
![]() $c_n <_P c_m$
if and only if
$c_n <_P c_m$
if and only if
![]() $n < m$
, and let
$n < m$
, and let
![]() $\ell _n <_P \ell _m$
if and only if
$\ell _n <_P \ell _m$
if and only if
![]() $\ell _n <_L \ell _m$
. Moreover, for each
$\ell _n <_L \ell _m$
. Moreover, for each
![]() $n \leq m$
, define:
$n \leq m$
, define:
-
(1)
 $c_m <_P \ell _n$
if
$c_m <_P \ell _n$
if
 $\forall k \, (n < k \leq m \;\rightarrow \; f(n) < f(k))$
(i.e., if n is true at stage m), and
$\forall k \, (n < k \leq m \;\rightarrow \; f(n) < f(k))$
(i.e., if n is true at stage m), and
 $c_m \mid _P \ell _n$
otherwise;
$c_m \mid _P \ell _n$
otherwise; -
(2)
 $c_n <_P \ell _m$
.
$c_n <_P \ell _m$
.
Notice that
![]() $c_n <_P \ell _n$
for every n.
$c_n <_P \ell _n$
for every n.
We must verify that
![]() $(P, <_P)$
is a partial order. Clearly
$(P, <_P)$
is a partial order. Clearly
![]() $<_P$
is irreflexive, so we check that
$<_P$
is irreflexive, so we check that
![]() $<_P$
is transitive. For no
$<_P$
is transitive. For no
![]() $a, b \in \mathbb {N}$
it is the case that
$a, b \in \mathbb {N}$
it is the case that
![]() $\ell _a <_P c_b$
, so we need only verify the following four cases.
$\ell _a <_P c_b$
, so we need only verify the following four cases.
-
• If
 $\ell _a <_P \ell _b$
and
$\ell _a <_P \ell _b$
and
 $\ell _b <_P \ell _d$
for some
$\ell _b <_P \ell _d$
for some
 $a, b, d \in \mathbb {N}$
, then
$a, b, d \in \mathbb {N}$
, then
 $\ell _a <_P \ell _d$
because the restriction of
$\ell _a <_P \ell _d$
because the restriction of
 $<_P$
to L is a linear order.
$<_P$
to L is a linear order. -
• Similarly, if
 $c_a <_P c_b$
and
$c_a <_P c_b$
and
 $c_b <_P c_d$
for some
$c_b <_P c_d$
for some
 $a, b, d \in \mathbb {N}$
, then
$a, b, d \in \mathbb {N}$
, then
 $c_a <_P c_d$
because the restriction of
$c_a <_P c_d$
because the restriction of
 $<_P$
to
$<_P$
to
 $\{c_n : n \in \mathbb {N}\}$
is a linear order.
$\{c_n : n \in \mathbb {N}\}$
is a linear order. -
• Suppose that
 $c_s <_P c_m$
and
$c_s <_P c_m$
and
 $c_m <_P \ell _n$
for some
$c_m <_P \ell _n$
for some
 $s, m, n \in \mathbb {N}$
with
$s, m, n \in \mathbb {N}$
with
 $s \neq m$
. Notice that
$s \neq m$
. Notice that
 $c_s <_P c_m$
implies
$c_s <_P c_m$
implies
 $s < m$
. If
$s < m$
. If
 $s \leq n$
, then from condition (2) we immediately obtain
$s \leq n$
, then from condition (2) we immediately obtain
 $c_s <_P \ell _n$
. If instead
$c_s <_P \ell _n$
. If instead
 $n < s$
, then
$n < s$
, then
 $n < s < m$
. That
$n < s < m$
. That
 $c_m <_P \ell _n$
means that n is true at stage m by condition (1). Thus n is also true at stage s, so
$c_m <_P \ell _n$
means that n is true at stage m by condition (1). Thus n is also true at stage s, so
 $c_s <_P \ell _n$
as well.
$c_s <_P \ell _n$
as well. -
• Finally, suppose that
 $c_s <_P \ell _m$
and
$c_s <_P \ell _m$
and
 $\ell _m <_P \ell _n$
for some
$\ell _m <_P \ell _n$
for some
 $s, m, n \in \mathbb {N}$
with
$s, m, n \in \mathbb {N}$
with
 $m \neq n$
. If
$m \neq n$
. If
 $s \leq n$
, then it follows immediately from condition (2) that
$s \leq n$
, then it follows immediately from condition (2) that
 $c_s <_P \ell _n$
. So suppose that
$c_s <_P \ell _n$
. So suppose that
 $n < s$
. We claim that
$n < s$
. We claim that
 $n < m$
. Suppose on the contrary that
$n < m$
. Suppose on the contrary that
 $m < n$
. Then m is false at stage n by Construction 4.4 because
$m < n$
. Then m is false at stage n by Construction 4.4 because
 $\ell _m <_P \ell _n$
. Thus m is false at stage s as well because
$\ell _m <_P \ell _n$
. Thus m is false at stage s as well because
 $m < n < s$
, and this contradicts
$m < n < s$
, and this contradicts
 $c_s <_P \ell _m$
. We therefore have that
$c_s <_P \ell _m$
. We therefore have that
 $n < s$
, that
$n < s$
, that
 $n < m$
, and that n is true at stage m because
$n < m$
, and that n is true at stage m because
 $\ell _m <_P \ell _n$
. If
$\ell _m <_P \ell _n$
. If
 $s \leq m$
, then
$s \leq m$
, then
 $n < s \leq m$
, so n is true at stage s as well, and we have
$n < s \leq m$
, so n is true at stage s as well, and we have
 $c_s <_P \ell _n$
as desired. Otherwise
$c_s <_P \ell _n$
as desired. Otherwise
 $m < s$
, so
$m < s$
, so
 $n < m < s$
and m is true at stage s because
$n < m < s$
and m is true at stage s because
 $c_s <_P \ell _m$
. Suppose for a contradiction that n is false at stage s. Then there is a k with
$c_s <_P \ell _m$
. Suppose for a contradiction that n is false at stage s. Then there is a k with
 $n < k \leq s$
and
$n < k \leq s$
and
 $f(k) < f(n)$
. It must be that
$f(k) < f(n)$
. It must be that
 $k> m$
because otherwise k would witness that n is false at stage m. It must therefore also be that
$k> m$
because otherwise k would witness that n is false at stage m. It must therefore also be that
 $f(m) < f(k)$
because otherwise k would witness that m is false at stage s. Thus
$f(m) < f(k)$
because otherwise k would witness that m is false at stage s. Thus
 $f(m) < f(k) < f(n)$
, so in fact m witnesses that n is false at stage m, which is a contradiction. Thus n is true at stage s, so
$f(m) < f(k) < f(n)$
, so in fact m witnesses that n is false at stage m, which is a contradiction. Thus n is true at stage s, so
 $c_s <_P \ell _n$
.
$c_s <_P \ell _n$
.
We conclude that
![]() $(P, <_P)$
is indeed a partial order. Let C be the chain
$(P, <_P)$
is indeed a partial order. Let C be the chain
![]() $C = \{c_n : n \in \mathbb {N}\}$
, and let D be a maximal chain in P with
$C = \{c_n : n \in \mathbb {N}\}$
, and let D be a maximal chain in P with
![]() $C \subseteq D$
. Then
$C \subseteq D$
. Then
![]() $\{n : \ell _n \in D\}$
is the set of true numbers for f. To see this, first observe that if n is true, then
$\{n : \ell _n \in D\}$
is the set of true numbers for f. To see this, first observe that if n is true, then
![]() $\ell _n$
is comparable with every element of P, so
$\ell _n$
is comparable with every element of P, so
![]() $\ell _n$
must be in D by maximality. On the other hand, if n is false, then there is a
$\ell _n$
must be in D by maximality. On the other hand, if n is false, then there is a
![]() $m> n$
with
$m> n$
with
![]() $f(m) < f(n)$
witnessing that n is false. Then
$f(m) < f(n)$
witnessing that n is false. Then
![]() $c_m \mid _P \ell _n$
, so
$c_m \mid _P \ell _n$
, so
![]() $\ell _n$
cannot be in D. The true numbers for f thus form a set, and therefore the range of f exists as a set. This implies
$\ell _n$
cannot be in D. The true numbers for f thus form a set, and therefore the range of f exists as a set. This implies
![]() $\mathsf {ACA}_0$
by Lemma 2.1.
$\mathsf {ACA}_0$
by Lemma 2.1.
The partial order constructed in the reverse direction of Proposition 8.2 is
![]() $2$
-chain decomposable. Thus Proposition 8.2 item (2) remains equivalent to
$2$
-chain decomposable. Thus Proposition 8.2 item (2) remains equivalent to
![]() $\mathsf {ACA}_0$
when restricted to
$\mathsf {ACA}_0$
when restricted to
![]() $2$
-chain decomposable partial orders or to partial orders of width
$2$
-chain decomposable partial orders or to partial orders of width
![]() $\leq \! 2$
. Extending a given antichain to a maximal antichain in a partial order is also equivalent to
$\leq \! 2$
. Extending a given antichain to a maximal antichain in a partial order is also equivalent to
![]() $\mathsf {ACA}_0$
over
$\mathsf {ACA}_0$
over
![]() $\mathsf {RCA}_0$
by [Reference Frittaion and Marcone13, Lemma 5.5].
$\mathsf {RCA}_0$
by [Reference Frittaion and Marcone13, Lemma 5.5].
Finally, we turn to
![]() $\mathsf {MMLC}$
and show that it is equivalent to
$\mathsf {MMLC}$
and show that it is equivalent to
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
over
$\Pi ^1_1\text {-}\mathsf {CA}_0$
over
![]() $\mathsf {RCA}_0$
, even when restricted to linear orders. Consider a partial order
$\mathsf {RCA}_0$
, even when restricted to linear orders. Consider a partial order
![]() $(P, <_P)$
. The axiomatic difficulty in producing a maximal max-less chain in P is in determining whether a given
$(P, <_P)$
. The axiomatic difficulty in producing a maximal max-less chain in P is in determining whether a given
![]() $p \in P$
can be a member of a max-less chain. It is easy to see that p is a member of a max-less chain if and only if
$p \in P$
can be a member of a max-less chain. It is easy to see that p is a member of a max-less chain if and only if
![]() $p{\uparrow }$
is reverse ill-founded. However, this is a
$p{\uparrow }$
is reverse ill-founded. However, this is a
![]() $\Sigma ^1_1$
property of p, and we show that producing the set of such p requires
$\Sigma ^1_1$
property of p, and we show that producing the set of such p requires
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
in general. For the reversal, recall the Kleene–Brouwer ordering of
$\Pi ^1_1\text {-}\mathsf {CA}_0$
in general. For the reversal, recall the Kleene–Brouwer ordering of
![]() $\mathbb {N}^{<\mathbb {N}}$
, whereby
$\mathbb {N}^{<\mathbb {N}}$
, whereby
![]() $\tau <_{\mathrm {KB}} \sigma $
if either
$\tau <_{\mathrm {KB}} \sigma $
if either
![]() $\tau $
is a proper extension of
$\tau $
is a proper extension of
![]() $\sigma $
or
$\sigma $
or
![]() $\tau $
is to the left of
$\tau $
is to the left of
![]() $\sigma $
. That is,
$\sigma $
. That is,
![]() $\tau <_{\mathrm {KB}} \sigma $
if and only if
$\tau <_{\mathrm {KB}} \sigma $
if and only if
Theorem 8.3. The following are equivalent over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
-
(1)
 $\Pi ^1_1\text {-}\mathsf {CA}_0$
.
$\Pi ^1_1\text {-}\mathsf {CA}_0$
. -
(2)
 $\mathsf {MMLC}$
.
$\mathsf {MMLC}$
. -
(3)
 $\mathsf {MMLC}$
restricted to linear orders.
$\mathsf {MMLC}$
restricted to linear orders. -
(4) For every partial order
 $(P, <_P)$
, there is a set
$(P, <_P)$
, there is a set
 $W \subseteq P$
such that
$W \subseteq P$
such that
 $\forall p \in P \; (p \in W \;\leftrightarrow \; p{\downarrow } \text { is well-founded})$
.
$\forall p \in P \; (p \in W \;\leftrightarrow \; p{\downarrow } \text { is well-founded})$
. -
(5) For every linear order
 $(L, <_P)$
, there is a set
$(L, <_P)$
, there is a set
 $W \subseteq L$
such that
$W \subseteq L$
such that
 $\forall \ell \in L \; (\ell \in W \;\leftrightarrow \; \ell {\downarrow } \text { is well-founded})$
.
$\forall \ell \in L \; (\ell \in W \;\leftrightarrow \; \ell {\downarrow } \text { is well-founded})$
.
Proof For (1)
![]() $\Rightarrow $
(2), let
$\Rightarrow $
(2), let
![]() $(P, <_P)$
be a partial order. Use
$(P, <_P)$
be a partial order. Use
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
(and the fact that the
$\Pi ^1_1\text {-}\mathsf {CA}_0$
(and the fact that the
![]() $\Sigma ^1_1$
sets are the complements of the
$\Sigma ^1_1$
sets are the complements of the
![]() $\Pi ^1_1$
sets) to define the set
$\Pi ^1_1$
sets) to define the set
![]() $Q = \{q \in P : q{\uparrow } \text { is reverse ill-founded}\}$
, and consider the partial order
$Q = \{q \in P : q{\uparrow } \text { is reverse ill-founded}\}$
, and consider the partial order
![]() $(Q, <_P)$
. Let C be a maximal chain in Q, which may be produced in
$(Q, <_P)$
. Let C be a maximal chain in Q, which may be produced in
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
We first show that C is max-less. To see this, suppose for a contradiction that C has a maximum element m. Then
![]() $m \in C \subseteq Q$
, so
$m \in C \subseteq Q$
, so
![]() $m{\uparrow }$
is reverse ill-founded in P. Thus there is an infinite ascending sequence
$m{\uparrow }$
is reverse ill-founded in P. Thus there is an infinite ascending sequence
![]() $m <_P a_0 <_P a_1 <_P a_2 <_P \cdots $
in P. Each
$m <_P a_0 <_P a_1 <_P a_2 <_P \cdots $
in P. Each
![]() $a_i{\uparrow }$
is reverse ill-founded in P as well, so
$a_i{\uparrow }$
is reverse ill-founded in P as well, so
![]() $\{a_i : i \in \mathbb {N}\} \subseteq Q$
. Then
$\{a_i : i \in \mathbb {N}\} \subseteq Q$
. Then
![]() $C \cup \{a_i : i \in \mathbb {N}\} \subseteq Q$
is a chain in Q properly extending C, contradicting that C is a maximal chain in Q. Thus C is max-less.
$C \cup \{a_i : i \in \mathbb {N}\} \subseteq Q$
is a chain in Q properly extending C, contradicting that C is a maximal chain in Q. Thus C is max-less.
We now show that C is maximal among the max-less chains of P. Suppose that
![]() $D \subseteq P$
is a max-less chain with
$D \subseteq P$
is a max-less chain with
![]() $C \subseteq D$
. Let
$C \subseteq D$
. Let
![]() $d \in D$
. As D is max-less, we may define an infinite ascending sequence
$d \in D$
. As D is max-less, we may define an infinite ascending sequence
![]() $d = d_0 <_P d_1 <_P d_2 <_P \cdots $
of elements of D. Thus
$d = d_0 <_P d_1 <_P d_2 <_P \cdots $
of elements of D. Thus
![]() $d{\uparrow }$
is reverse ill-founded in P, so
$d{\uparrow }$
is reverse ill-founded in P, so
![]() $d \in Q$
. This shows that
$d \in Q$
. This shows that
![]() $D \subseteq Q$
. That is, C and D are chains in Q with
$D \subseteq Q$
. That is, C and D are chains in Q with
![]() $C \subseteq D$
. Therefore
$C \subseteq D$
. Therefore
![]() $C = D$
by the maximality of C in Q. Thus C is a maximal max-less chain in P.
$C = D$
by the maximality of C in Q. Thus C is a maximal max-less chain in P.
We have that (1)
![]() $\Rightarrow $
(4) because the set W required by item (4) is
$\Rightarrow $
(4) because the set W required by item (4) is
![]() $\Pi ^1_1$
. Furthermore, (2)
$\Pi ^1_1$
. Furthermore, (2)
![]() $\Rightarrow $
(3) because item (3) is a special case of item (2), and likewise (4)
$\Rightarrow $
(3) because item (3) is a special case of item (2), and likewise (4)
![]() $\Rightarrow $
(5) because item (5) is a special case of item (4).
$\Rightarrow $
(5) because item (5) is a special case of item (4).
For (3)
![]() $\Rightarrow $
(5), let
$\Rightarrow $
(5), let
![]() $(L, <_L)$
be a linear order, and by item (3) applied to the reverse of L, let C be a maximal min-less chain in L. Then C consists of exactly the
$(L, <_L)$
be a linear order, and by item (3) applied to the reverse of L, let C be a maximal min-less chain in L. Then C consists of exactly the
![]() $\ell \in L$
for which
$\ell \in L$
for which
![]() $\ell {\downarrow }$
is ill-founded. If
$\ell {\downarrow }$
is ill-founded. If
![]() $\ell \in C$
, then there is an infinite descending sequence in C below
$\ell \in C$
, then there is an infinite descending sequence in C below
![]() $\ell $
because C is min-less. Thus
$\ell $
because C is min-less. Thus
![]() $\ell {\downarrow }$
is ill-founded. Conversely, consider an
$\ell {\downarrow }$
is ill-founded. Conversely, consider an
![]() $\ell \in L$
with
$\ell \in L$
with
![]() $\ell {\downarrow }$
ill-founded. Then there is an infinite descending sequence
$\ell {\downarrow }$
ill-founded. Then there is an infinite descending sequence
![]() $\ell = d_0>_L d_1 >_L d_2 >_L \cdots $
in L below
$\ell = d_0>_L d_1 >_L d_2 >_L \cdots $
in L below
![]() $\ell $
. Thin the sequence so that its range exists as a set D with
$\ell $
. Thin the sequence so that its range exists as a set D with
![]() $\ell \in D$
. Then C and D are both min-less, so
$\ell \in D$
. Then C and D are both min-less, so
![]() $C \cup D$
is min-less as well, plus
$C \cup D$
is min-less as well, plus
![]() $C \cup D$
is a chain because every subset of a linear order is a chain. Therefore
$C \cup D$
is a chain because every subset of a linear order is a chain. Therefore
![]() $C = C \cup D$
by the maximality of C, so
$C = C \cup D$
by the maximality of C, so
![]() $\ell \in C$
. Thus
$\ell \in C$
. Thus
![]() $W = L \setminus C$
consists of exactly the
$W = L \setminus C$
consists of exactly the
![]() $\ell \in L$
for which
$\ell \in L$
for which
![]() $\ell {\downarrow }$
is well-founded.
$\ell {\downarrow }$
is well-founded.
To finish the proof, it suffices to show that (5)
![]() $\Rightarrow $
(1). To do this, we show that item (5) implies the leftmost path principle
$\Rightarrow $
(1). To do this, we show that item (5) implies the leftmost path principle
![]() $\mathsf {LPP}$
, which is equivalent to
$\mathsf {LPP}$
, which is equivalent to
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
over
$\Pi ^1_1\text {-}\mathsf {CA}_0$
over
![]() $\mathsf {RCA}_0$
by Theorem 2.2. Let
$\mathsf {RCA}_0$
by Theorem 2.2. Let
![]() $T \subseteq \mathbb {N}^{<\mathbb {N}}$
be an ill-founded tree, and apply item (5) to the linear order
$T \subseteq \mathbb {N}^{<\mathbb {N}}$
be an ill-founded tree, and apply item (5) to the linear order
![]() $(T, <_{\mathrm {KB}})$
(and take complements) to obtain the set I of
$(T, <_{\mathrm {KB}})$
(and take complements) to obtain the set I of
![]() $\sigma \in T$
such that
$\sigma \in T$
such that
![]() $\sigma {\downarrow }$
is ill-founded with respect to
$\sigma {\downarrow }$
is ill-founded with respect to
![]() $<_{\mathrm {KB}}$
. Notice that I is a subtree of T and that I has no
$<_{\mathrm {KB}}$
. Notice that I is a subtree of T and that I has no
![]() $<_{\mathrm {KB}}$
-minimum element.
$<_{\mathrm {KB}}$
-minimum element.
Recursively define the following a priori possibly partial function
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
such that for every n, if
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
such that for every n, if
![]() $f {\restriction } n$
is defined, then
$f {\restriction } n$
is defined, then
![]() $f {\restriction } n \in I$
. Given n, if
$f {\restriction } n \in I$
. Given n, if
![]() $f {\restriction } n$
is defined, let m be least such that
$f {\restriction } n$
is defined, let m be least such that
![]() $(f {\restriction } n)^{\smallfrown } m \in I$
(if there is such an m) and set
$(f {\restriction } n)^{\smallfrown } m \in I$
(if there is such an m) and set
![]() $f(n) = m$
. We show that f is total. Suppose for a contradiction that f is partial, and by the
$f(n) = m$
. We show that f is total. Suppose for a contradiction that f is partial, and by the
![]() $\Pi ^0_1$
least element principle, let n be least such that
$\Pi ^0_1$
least element principle, let n be least such that
![]() $f(n)$
is undefined. Then
$f(n)$
is undefined. Then
![]() $f {\restriction } n$
is defined and in I. As I has no
$f {\restriction } n$
is defined and in I. As I has no
![]() $<_{\mathrm {KB}}$
-least element, let
$<_{\mathrm {KB}}$
-least element, let
![]() $\tau \in I$
be such that
$\tau \in I$
be such that
![]() $\tau <_{\mathrm {KB}} f {\restriction } n$
. If
$\tau <_{\mathrm {KB}} f {\restriction } n$
. If
![]() $\tau $
is to the left of
$\tau $
is to the left of
![]() $f {\restriction } n$
, then let
$f {\restriction } n$
, then let
![]() $j < n$
be such that
$j < n$
be such that
![]() $\tau (j) < f(j)$
and
$\tau (j) < f(j)$
and
![]() $\tau {\restriction } j = f {\restriction } j$
. Then
$\tau {\restriction } j = f {\restriction } j$
. Then
![]() $\tau {\restriction } (j+1) = (f {\restriction } j)^{\smallfrown } \tau (j)$
is in I and
$\tau {\restriction } (j+1) = (f {\restriction } j)^{\smallfrown } \tau (j)$
is in I and
![]() $\tau (j) < f(j)$
, which contradicts the definition of
$\tau (j) < f(j)$
, which contradicts the definition of
![]() $f(j)$
. On the other hand, if
$f(j)$
. On the other hand, if
![]() $\tau \succ f {\restriction } n$
, then
$\tau \succ f {\restriction } n$
, then
![]() $|\tau |> n$
and
$|\tau |> n$
and
![]() $\tau {\restriction } (n+1) = (f {\restriction } n)^{\smallfrown } \tau (n)$
is in I. Thus there is an m such that
$\tau {\restriction } (n+1) = (f {\restriction } n)^{\smallfrown } \tau (n)$
is in I. Thus there is an m such that
![]() $(f {\restriction } n)^{\smallfrown } m$
is in I, and therefore there is a least such m. Thus
$(f {\restriction } n)^{\smallfrown } m$
is in I, and therefore there is a least such m. Thus
![]() $f(n)$
is defined, which is a contradiction. Therefore f is total. Thus f is an infinite path through I and hence is an infinite path through T. We show that f is the leftmost infinite path through T.
$f(n)$
is defined, which is a contradiction. Therefore f is total. Thus f is an infinite path through I and hence is an infinite path through T. We show that f is the leftmost infinite path through T.
Consider an infinite path g through T. Then
![]() $g {\restriction } 0>_{\mathrm {KB}} g {\restriction } 1 >_{\mathrm {KB}} g {\restriction } 2 >_{\mathrm {KB}} \cdots $
is an infinite
$g {\restriction } 0>_{\mathrm {KB}} g {\restriction } 1 >_{\mathrm {KB}} g {\restriction } 2 >_{\mathrm {KB}} \cdots $
is an infinite
![]() $<_{\mathrm {KB}}$
-descending sequence. Thus
$<_{\mathrm {KB}}$
-descending sequence. Thus
![]() $(g {\restriction } n){\downarrow }$
is ill-founded for every n, so
$(g {\restriction } n){\downarrow }$
is ill-founded for every n, so
![]() $g {\restriction } n \in I$
for every n. Now suppose for a contradiction that g is to the left of f. Then there is an n such that
$g {\restriction } n \in I$
for every n. Now suppose for a contradiction that g is to the left of f. Then there is an n such that
![]() $g(n) < f(n)$
and
$g(n) < f(n)$
and
![]() $g {\restriction } n = f {\restriction } n$
. Thus
$g {\restriction } n = f {\restriction } n$
. Thus
![]() $g {\restriction } (n+1) = (f {\restriction } n)^{\smallfrown } g(n)$
is in I and
$g {\restriction } (n+1) = (f {\restriction } n)^{\smallfrown } g(n)$
is in I and
![]() $g(n) < f(n)$
, which contradicts the definition of
$g(n) < f(n)$
, which contradicts the definition of
![]() $f(n)$
. Therefore g cannot be to the left of f, so f is the leftmost path through T. This concludes the proof of
$f(n)$
. Therefore g cannot be to the left of f, so f is the leftmost path through T. This concludes the proof of
![]() $\mathsf {LPP}$
.
$\mathsf {LPP}$
.
By taking complements and/or reversing the order, the statement “
![]() $p{\downarrow }$
is well-founded” may be replaced by any of “
$p{\downarrow }$
is well-founded” may be replaced by any of “
![]() $p{\downarrow }$
is ill-founded,” “
$p{\downarrow }$
is ill-founded,” “
![]() $p{\uparrow }$
is reverse well-founded,” and “
$p{\uparrow }$
is reverse well-founded,” and “
![]() $p{\uparrow }$
is reverse ill-founded” in Theorem 8.3 item (4), and the analogous replacement may be made in item (5) as well.
$p{\uparrow }$
is reverse ill-founded” in Theorem 8.3 item (4), and the analogous replacement may be made in item (5) as well.
Acknowledgments
We thank Keita Yokoyama for helpful discussions, especially concerning the formalization of Kierstead’s theorem in
![]() $\mathsf {RCA}_0$
. We thank our anonymous reviewer for several helpful suggestions. The opinions expressed in this work are those of the authors and do not necessarily reflect the views of the John Templeton Foundation.
$\mathsf {RCA}_0$
. We thank our anonymous reviewer for several helpful suggestions. The opinions expressed in this work are those of the authors and do not necessarily reflect the views of the John Templeton Foundation.
Funding
For their generous support, we thank the Workshop on Ramsey Theory and Computability at the University of Notre Dame Rome Global Gateway; Dagstuhl Seminar 18361: Measuring the Complexity of Computational Content: From Combinatorial Problems to Analysis; the BIRS/CMO workshop 19w5111: Reverse Mathematics of Combinatorial Principles; and the University of Leeds School of Mathematics Research Visitors’ Centre. Fiori-Carones was supported by the Mathematical Center in Akademgorodok under the agreement no. 75-15-2022-281 with the Ministry of Science and Higher Education of the Russian Federation. Marcone was supported by the departmental PRID funding HiWei—The higher levels of the Weihrauch hierarchy and by the Italian PRIN 2017 grant Mathematical Logic: models, sets, computability. Shafer was supported by the John Templeton Foundation grant ID 60842 A new dawn of intuitionism: mathematical and philosophical advances and by EPSRC grant EP/T031476/1 Reverse mathematics of general topology.