Article contents
Eine Bemerkung zu Henkin's Beweis für die Vollständigkeit des Prädikatenkalküls der ersten Stufe
Published online by Cambridge University Press: 12 March 2014
Extract
Im Folgenden wird eine Vereinfachung der Beweisanordnung für Henkin's Theorem [2] p. 162 angegeben (Abschnitt I). – Die Vereinfachung zeigt sich u.a. darin, daß für den abgeänderten Beweis eine Abschätzung der “projektiven Klasse” (im Sinne der Kleene-Mostowski'schen Theorie der projektiven Mengen von natürlichen Zahlen) für das zu konstruierende Modell gelingt (Abschnitte II–IV). Die Kenntnis der Henkin'schen Arbeit wird vorausgesetzt.
Um eine maximale widerspruchsfreie Menge Γω von geschlossenen Formeln, in der zu jeder Existenzaussage (∃x)A(x) eine Beispielaussage A(uij) vorhanden ist, zu erhalten, führt Henkin einen Turm von Kalkülen S0, S1, …, Si, … und dessen Vereinigung Sω ein. Abwechselnd wird dann die gegebene Menge von Formeln in Si zu einer maximalen widerspruchsfreien Menge Γi erweitert und in Si+1 durch Hinzunahme von Beispielaussagen für alle Existenzaussagen aus Γi ergänzt, für die das nicht schon in einem früheren Schritt geschehen ist. Γω ist dann die Vereinigung aller Γi.
Die Vereinfachung besteht nun darin, daß – nach Erweiterung von S0 zu einem Kalkül S* durch Hinzunahme einer einfachen Folge u1, u2, … von “neuen” Konstanten – in S* zu jeder Existenzaussage eine bedingte Beispielaussage gebildet wird. K sei die Klasse dieser Aussagen, Λ die gegebene widerspruchsfreie Menge; dann wird Λ* = K ◡ Λ in S* einmal zu einer maximalen widerspruchsfreien Menge ergänzt.
Unter Verwendung der Standard-Anordnung aller geschlossenen Formeln von S* erhalten wir für diejenigen von der Form (∃x)A(x) eine Aufzählung (∃x)Ai(x), dazu eine Indexfolge ji (i =1, 2, …), definiert durch:
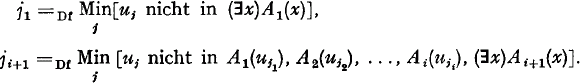
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1953
References
LITERATUR
- 27
- Cited by


