Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T03:57:24.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Doughnuts, floating ordinals, square brackets, and ultraflitters

Published online by Cambridge University Press:  12 March 2014

Carlos A. Di Prisco  and
James M. Henle
Carlos A. Di Prisco
Affiliation:
Instituto Venezolano de Investigaciones Cientificas, Apartado 21827, Caracas 1020-A, Venezuela, E-mail: [email protected]
James M. Henle
Affiliation:
Smith College, Northampton, Massachusetts 01063, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, we study partition properties of the set of real numbers. The meaning of “set of real numbers” will vary, referring at times to the collection of sequences of natural numbers, ωω; the collection of infinite sets of natural numbers [ω]ω; the collection of infinite sequences of zeroes and ones, 2ω; or 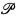(ω), the power set of ω.

The archetype for the relations is the property: “all sets of reals are Ramsey,” in the notation of Erdős and Hajnal, ω → (ω)ω. This states that for every partition F : [ω]ω → 2, there is an infinite set H ∈ [ω]ω such that F is constant on [H]ω. Like virtually all of the properties we will discuss, it contradicts the Axiom of Choice but is compatible with the principle of dependent choices (DC). DC will be used throughout the paper wihtout further mention.

The properties discussed in this paper will vary in two respects. Some, like ω → (ω)ω, will be incompatible with the existence of an ultrafilter on ω (UF) and some will not. Some are known to be consistent relative to ZF alone, and for some, such as ω → (ω)ω, the question is still open. All properties, however, are true in Solovay's model and hence are consistent relative to Con(ZF + “there exists an inaccessible cardinal”).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 65 , Issue 1 , March 2000 , pp. 461 - 473
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Carlson, T. J. and Simpson, S. G., A dual form of Ramsey's theorem, Advances in Mathematics, vol. 53 (1984), pp. 265–290.CrossRefGoogle Scholar
[2]Prisco, C. A. Di and Henle, J., Partitions of products, this Journal, vol. 58 (1993), pp. 860–871.Google Scholar
[3]Prisco, C. A. Di and Henle, J., Partitions of the reals and choice, Models, algebras and proofs (Caicedo, X. and Montenegro, C., editors), Selected papers of the X Latin American Symposium on Mathematical Logic, Marcel Dekker, 1999.Google Scholar
[4]Erdős, P. and Rado, R., A partition calculus in set theory, Bulletin of the American Mathematical Society, vol. 62 (1956), pp. 427–489.CrossRefGoogle Scholar
[5]Henle, J., On the consistency of one fixed omega, this Journal, vol. 60 (1995), pp. 172–177.Google Scholar
[6]Kleinberg, E. M., personal communication, c. 1975.Google Scholar
[7]Llopis, J., A note on polarized partitions, Notas de Lógica Matemática INMABB-CONICET, Bahia Blanca, Argentina, vol. 39 (1993).Google Scholar
[8]Llopis, J. and Todorcevic, S., Borel partitions of products of finite sets, Acta Científica Venezolana, vol. 47 (1996).Google Scholar
[9]Mathias, A. R. D., Happy families, Annals of Mathematical Logic, vol. 12 (1977), pp. 59–111.CrossRefGoogle Scholar
[10]Moran, G. and Strauss, D., Countable partitions of products, Mathematika, vol. 27 (1980), pp. 213–224.CrossRefGoogle Scholar
[11]Shelah, S., Can you take Solovay's inaccessible away?, Israel Journal of Mathematics, vol. 48 (1984), pp. 1–47.CrossRefGoogle Scholar