Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-09T04:59:37.334Z Has data issue: false hasContentIssue false
  • English
  • Français

A discrete chain of degrees of index sets

Published online by Cambridge University Press:  12 March 2014

Louise Hay
Louise Hay*
Affiliation:
University of Illinoisat Chicago Circle Chicago, Illinois 60680
Get access Rights & Permissions [Opens in a new window]

Extract

Let {Wi} be a standard enumeration of all recursively enumerable (r.e.) sets, and for any class A of r.e. sets, let θA denote the index set of A = {n ∣ Wn ∈ A}. (Clearly, 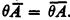.) In [1], the index sets of nonempty finite classes of finite sets were classified under one-one reducibility into an increasing sequence {Ym}, 0 ≤ m < ∞. In this paper we examine further properties of this sequence within the partial ordering of one-one degrees of index sets. The main results are as follows: (1) For each m, Ym < Ym + 1 and 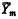< Ym + 1; (2) Ym is incomparable to 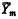; (3) Ym + 1 and 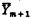; are immediate successors (among index sets) of Ym and 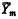m; (4) the pair (Ym + 1, 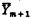) is a “least upper bound” for the pair (Ym, 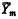) in the sense that any successor of both Ym and 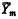is ≥ Ym + 1or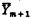; (5) the pair (Ym, 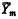) is a “greatest lower bound” for the pair (Ym + 1, 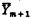) in the sense that any predecessor of both Ym + 1 and 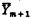is ≤ Ym or 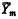. Since 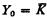and all Ym are in the bounded truth-table degree of K, this yields some local information about the one-one degrees of index sets which are “at the bottom” in the one-one ordering of index sets.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 1 , March 1972 , pp. 139 - 149
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[0]Dekker, J. C. E. and Myhill, J., Some theorems on classes of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 89 (1958), pp. 25–59.CrossRefGoogle Scholar
[1]Hay, L., Index sets of finite classes of recursively enumerable sets, this Journal, vol. 34 (1969), pp. 39–44.Google Scholar
[2]Myhill, J., Creative sets, Zeitschrift für mathematische Logik and Grundlagen der Mathematik, vol. 1 (1955), pp. 97–108.CrossRefGoogle Scholar
[3]Rogers, H. Jr., Computing degrees of unsolvability, Mathematisches Annalen, vol. 138 (1959), pp. 125–140.CrossRefGoogle Scholar
[4]Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar