Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-16T15:22:46.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Conditioned disjunction as a primitive connective for the erweiterter Aussagenkalkül

Published online by Cambridge University Press:  12 March 2014

Alan Rose
Alan Rose*
Affiliation:
King's College, Aberdeen, Scotland
Get access Rights & Permissions [Opens in a new window]

Extract

It has been shown that the conditioned disjunction function [X, Y, Z] with the same truth-table as (X & Y) ∨ (Z & 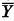) together with the logical constants t and f, form a complete set of independent connectives for the 2-valued propositional calculus and that these connectives are self-dual. This has since been generalised to the theorem which states that the conditioned disjunction function [Y, X1, X2, …, Xm, Y] with the same truth-table as (X1 & J1(Y)) ∨ (X2 & J2(Y)) ∨ … ∨ (Xm & Jm(Y)) together with the logical constants 1, 2, …, m form a complete set of independent connectives for the m-valued propositional calculus and that these connectives are self-dual. It has been conjectured by Church that conditioned disjunction together with the universal and existential quantifiers form a complete set of independent connectives for the 2-valued erweiterter Aussagenkalkül. The object of the present paper is to prove a theorem for the m-valued erweiterter Aussagenkalkül which reduces, in the case m = 2, to the conjecture of Church. In the m-valued propositional calculus if the propositional variable X occurs as a free variable in the formula 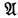then (∃X) 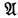and (X) 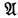are read “there exists X such that 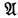” and “for all X, 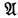”, respectively. If for a given assignment of truth-values to the remaining free propositional variables occurring in 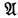, 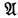takes the truth-value f(x), where x is the truth-value of X, then (∃X) 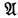and (X) 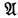take the truth-values min (f(1), f(2), …, f(m)), max(f(1), f(2), …, f(m)), respectively. We shall prove:

Theorem. The conditioned disjunction function, together with the universal and existential quantifiers, form a complete set of independent connectives for the m-valued erweiterter Aussagenkalkül.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 18 , Issue 1 , March 1953 , pp. 63 - 65
Copyright
Copyright © Association for Symbolic Logic 1953

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Church, Alonzo, Conditioned disjunction as a primitive connective for the prepositional calculus, Portugaliae Mathematica, vol. 7 (1948), pp. 87–90Google Scholar.

2 I.e. given any truth-table, a function with that truth-table can be defined in terms of the primitives, but if any one of the primitives is omitted there are functions which cannot be defined in terms of the remaining primitives.

3 Rose, Alan, Conditioned disjunction as a primitive connective for the m-valued prepositional calculus, Mathematische Annalen, vol. 123 (1951), pp. 76–78CrossRefGoogle Scholar.

4 The J-functions are those used by Rosser, J. B. and Turquette, A. R. in their paper Axiom schemes for m-valued prepositional calculi, this Journal, vol. 10 (1945), pp. 61–82Google Scholar.

5 Op. cit.

6 See Łukasiewicz, Jan and Tarski, Alfred, Untersuchungen über den Aussagenkalkül, Comptes rendus des séances de la Société des Sciences et des Lettres de Varsovie, Classe III, vol. 23 (1930), pp. 30–50Google Scholar; also Russell, B., The theory of implication, American Journal of Mathematics, vol. 28 (1906), pp. 159–202CrossRefGoogle Scholar.

7 It may be necessary first to rename some of the bound variables occurring in i, in order to avoid collision between free and bound variables.

8 If always takes the same truth-value as Ψ(X 1, X 2, …, Xn), where the symbol “−” denotes the negation function of Łukasiewicz (op. cit.), then Φ is said to be the dual of Ψ.