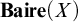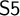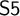1 Introduction
Canonical examples of Boolean algebras include the powerset
![]() $\wp (X)$
of a set X, as well as its subalgebras; indeed, every Boolean algebra is isomorphic to a subalgebra of a powerset algebra (see, e.g., [Reference Koppelberg19, p. 28]). Alternately, one can consider quotients of the form
$\wp (X)$
of a set X, as well as its subalgebras; indeed, every Boolean algebra is isomorphic to a subalgebra of a powerset algebra (see, e.g., [Reference Koppelberg19, p. 28]). Alternately, one can consider quotients of the form
![]() $\wp (X)/ \mathbf {I}$
, where
$\wp (X)/ \mathbf {I}$
, where
![]() $\mathbf {I}$
is a suitable ideal of
$\mathbf {I}$
is a suitable ideal of
![]() $\wp (X)$
. Some of the most familiar such ideals are the ideal
$\wp (X)$
. Some of the most familiar such ideals are the ideal
![]() $\mathbf N$
of null sets when X is a measure space (see, e.g., [Reference Koppelberg19, p. 233]), or the ideal
$\mathbf N$
of null sets when X is a measure space (see, e.g., [Reference Koppelberg19, p. 233]), or the ideal
![]() $\mathbf {M}$
of meager sets when X is a topological space (see, e.g., [Reference Koppelberg19, p. 182]); recall that a set is nowhere dense if the interior of its closure is empty, and that it is meager if it is a countable union of nowhere dense sets. The quotient
$\mathbf {M}$
of meager sets when X is a topological space (see, e.g., [Reference Koppelberg19, p. 182]); recall that a set is nowhere dense if the interior of its closure is empty, and that it is meager if it is a countable union of nowhere dense sets. The quotient
![]() $\wp (X) / \mathbf {M} $
gives rise to the Baire algebra of X.
$\wp (X) / \mathbf {M} $
gives rise to the Baire algebra of X.
When X is a topological space, the powerset algebra of X comes equipped with the usual closure operator
![]() $\mathbf {c} \colon \wp (X) \to \wp (X)$
. This operator satisfies some familiar properties also known as the Kuratowski axioms, including, e.g.,
$\mathbf {c} \colon \wp (X) \to \wp (X)$
. This operator satisfies some familiar properties also known as the Kuratowski axioms, including, e.g.,
![]() $A\subseteq \mathbf {c} A$
(see Section 2 for the full list), and any operator satisfying these axioms uniquely determines a topology on X. One can more generally consider a Boolean algebra B with an operator
$A\subseteq \mathbf {c} A$
(see Section 2 for the full list), and any operator satisfying these axioms uniquely determines a topology on X. One can more generally consider a Boolean algebra B with an operator
![]() $\mathbf {c} \colon B \to B$
satisfying the same axioms; such algebras are the closure algebras of McKinsey and Tarski [Reference McKinsey and Tarski24]. It is then a natural question to ask whether a closure operator on
$\mathbf {c} \colon B \to B$
satisfying the same axioms; such algebras are the closure algebras of McKinsey and Tarski [Reference McKinsey and Tarski24]. It is then a natural question to ask whether a closure operator on
![]() $\wp (X)$
carries over to quotients
$\wp (X)$
carries over to quotients
![]() $\wp (X)/\mathbf {I}$
in a meaningful way. This question has already been answered in the affirmative by Fernández-Duque [Reference Fernández-Duque12] and Lando [Reference Lando22] in the setting of the Lebesgue measure algebra, defined as the quotient of the Borel sets of reals modulo the null sets. In an unpublished work, Bjorndahl has also considered validity modulo the nowhere dense sets, although he does not work directly with the algebraic quotient. In this article, we will explore this question in the setting of the Baire algebra of a topological space X.
$\wp (X)/\mathbf {I}$
in a meaningful way. This question has already been answered in the affirmative by Fernández-Duque [Reference Fernández-Duque12] and Lando [Reference Lando22] in the setting of the Lebesgue measure algebra, defined as the quotient of the Borel sets of reals modulo the null sets. In an unpublished work, Bjorndahl has also considered validity modulo the nowhere dense sets, although he does not work directly with the algebraic quotient. In this article, we will explore this question in the setting of the Baire algebra of a topological space X.
One subtlety when defining a closure operator for such quotients is that, denoting the equivalence class of Y by
![]() $[Y]$
, the definition
$[Y]$
, the definition
![]() $\mathbf {c}[Y] : = [\mathbf {c} Y]$
does not yield a well-defined operation: for example, in the above-mentioned quotients,
$\mathbf {c}[Y] : = [\mathbf {c} Y]$
does not yield a well-defined operation: for example, in the above-mentioned quotients,
![]() $[\mathbb Q] = [\varnothing ]$
(as
$[\mathbb Q] = [\varnothing ]$
(as
![]() $\mathbb Q$
is both meager and of measure zero), yet
$\mathbb Q$
is both meager and of measure zero), yet
![]() $[\mathbf {c}\mathbb Q] = [\mathbb R]\neq [\varnothing ] = [\mathbf {c} \varnothing ]$
. Instead, we must compute the closure of a set directly within the quotient, by the expression
$[\mathbf {c}\mathbb Q] = [\mathbb R]\neq [\varnothing ] = [\mathbf {c} \varnothing ]$
. Instead, we must compute the closure of a set directly within the quotient, by the expression
where
![]() $\sqsubseteq $
denotes the partial order on the quotient algebra. We refer to the element
$\sqsubseteq $
denotes the partial order on the quotient algebra. We refer to the element
![]() $\mathbf {c} a$
as the Baire closure of a. We utilize a nontrivial fact in topology that the Boolean algebra of Borel sets of an arbitrary topological space modulo the ideal of meager sets is complete (see [Reference Sikorski28, p. 75]) to show that this produces a closure operator on the Baire algebra of any topological space X, and we denote the resulting closure algebra by
$\mathbf {c} a$
as the Baire closure of a. We utilize a nontrivial fact in topology that the Boolean algebra of Borel sets of an arbitrary topological space modulo the ideal of meager sets is complete (see [Reference Sikorski28, p. 75]) to show that this produces a closure operator on the Baire algebra of any topological space X, and we denote the resulting closure algebra by
![]() $\mathbf {Baire}(X) $
.
$\mathbf {Baire}(X) $
.
Much as Boolean algebras provide semantics for propositional logic, closure algebras provide semantics for modal logic, which extends propositional logic with an operator
![]() $\Diamond $
that we will interpret as a closure operator, along with its dual
$\Diamond $
that we will interpret as a closure operator, along with its dual
![]() $\Box $
, interpreted as interior. Such topological semantics of modal logic, as well as the closely related intuitionistic logic, predates their now-widespread relational semantics. For intuitionistic logic it was first developed by Stone [Reference Stone29] and Tarski [Reference Tarski30], and for modal logic by Tsao-Chen [Reference Tsao-Chen31], McKinsey [Reference McKinsey23], and McKinsey and Tarski [Reference McKinsey and Tarski24]. Under this interpretation, the modal logic of all topological spaces turns out to be the well-known modal system of Lewis,
$\Box $
, interpreted as interior. Such topological semantics of modal logic, as well as the closely related intuitionistic logic, predates their now-widespread relational semantics. For intuitionistic logic it was first developed by Stone [Reference Stone29] and Tarski [Reference Tarski30], and for modal logic by Tsao-Chen [Reference Tsao-Chen31], McKinsey [Reference McKinsey23], and McKinsey and Tarski [Reference McKinsey and Tarski24]. Under this interpretation, the modal logic of all topological spaces turns out to be the well-known modal system of Lewis,
![]() $\mathsf {S4}$
(see Section 2 for the definition). Other well-known extensions of
$\mathsf {S4}$
(see Section 2 for the definition). Other well-known extensions of
![]() $\mathsf {S4}$
also turn out to be the modal logics of interesting topological spaces. To give a couple of examples:
$\mathsf {S4}$
also turn out to be the modal logics of interesting topological spaces. To give a couple of examples:
-
•
 $\mathsf {S4.2}:= \mathsf {S4} + \Diamond \Box p\to \Box \Diamond p$
is the modal logic of all extremally disconnected spaces [Reference Gabelaia13].
$\mathsf {S4.2}:= \mathsf {S4} + \Diamond \Box p\to \Box \Diamond p$
is the modal logic of all extremally disconnected spaces [Reference Gabelaia13]. -
•
 $\mathsf {S4.3}:=\mathsf {S4} + \Box (\Box p\to q)\vee \Box (\Box q\to p)$
is the modal logic of all hereditarily extremally disconnected spaces [Reference Bezhanishvili, Bezhanishvili, Lucero-Bryan and van Mill1].
$\mathsf {S4.3}:=\mathsf {S4} + \Box (\Box p\to q)\vee \Box (\Box q\to p)$
is the modal logic of all hereditarily extremally disconnected spaces [Reference Bezhanishvili, Bezhanishvili, Lucero-Bryan and van Mill1].
Here we recall that a space X is extremally disconnected if the closure of each open set is open, and X is hereditarily extremally disconnected if each subspace of X is extremally disconnected.
These topological completeness results can be strengthened as follows. By the celebrated McKinsey–Tarski theorem [Reference McKinsey and Tarski24],
![]() $\mathsf {S4}$
is the modal logic of any crowded metrizable space.Footnote
1
In fact,
$\mathsf {S4}$
is the modal logic of any crowded metrizable space.Footnote
1
In fact,
![]() $\mathsf {S4}$
is strongly sound and complete with respect to any crowded metrizable space [Reference Kremer20, Reference Goldblatt and Hodkinson14]. In particular,
$\mathsf {S4}$
is strongly sound and complete with respect to any crowded metrizable space [Reference Kremer20, Reference Goldblatt and Hodkinson14]. In particular,
![]() $\mathsf {S4}$
is the modal logic of the real unit interval
$\mathsf {S4}$
is the modal logic of the real unit interval
![]() $[0,1]$
. On the other hand,
$[0,1]$
. On the other hand,
![]() $\mathsf {S4}.2$
is the modal logic of the Gleason cover of
$\mathsf {S4}.2$
is the modal logic of the Gleason cover of
![]() $[0,1]$
(see [Reference Bezhanishvili and Harding4]), while
$[0,1]$
(see [Reference Bezhanishvili and Harding4]), while
![]() $\mathsf {S4}.3$
is the modal logic of a countable (hereditarily) extremally disconnected subspace of the Gleason cover of
$\mathsf {S4}.3$
is the modal logic of a countable (hereditarily) extremally disconnected subspace of the Gleason cover of
![]() $[0,1]$
(see [Reference Bezhanishvili, Bezhanishvili, Lucero-Bryan and van Mill1]). In contrast,
$[0,1]$
(see [Reference Bezhanishvili, Bezhanishvili, Lucero-Bryan and van Mill1]). In contrast,
![]() $\mathsf {S5}:=\mathsf {S4} + \Diamond p \to \Box \Diamond p $
, which is one of the best known modal logics, is not complete with respect to any class of spaces that satisfy even weak separation axioms. Indeed,
$\mathsf {S5}:=\mathsf {S4} + \Diamond p \to \Box \Diamond p $
, which is one of the best known modal logics, is not complete with respect to any class of spaces that satisfy even weak separation axioms. Indeed,
![]() $\Diamond \Box p\to \Box p$
is valid in a topological space iff each open set is also closed. Thus, a
$\Diamond \Box p\to \Box p$
is valid in a topological space iff each open set is also closed. Thus, a
![]() $T_0$
-space validates
$T_0$
-space validates
![]() $\mathsf {S5}$
iff it is discrete.
$\mathsf {S5}$
iff it is discrete.
One can also characterize the modal logics of closure algebras that are not based on a powerset. Fernández-Duque [Reference Fernández-Duque12] and Lando [Reference Lando22] have shown that
![]() $\mathsf {S4}$
is the logic of the Lebesgue measure algebra, and in this article we will characterize the logic of Baire algebras. An element
$\mathsf {S4}$
is the logic of the Lebesgue measure algebra, and in this article we will characterize the logic of Baire algebras. An element
![]() $c\in \mathbf {Baire}(X)$
is closed (resp. open) if
$c\in \mathbf {Baire}(X)$
is closed (resp. open) if
![]() $c=[C]$
for some closed (resp. open) C. A distinguished feature of
$c=[C]$
for some closed (resp. open) C. A distinguished feature of
![]() $\mathbf {Baire}(X)$
is that
$\mathbf {Baire}(X)$
is that
![]() $c\in \mathbf {Baire}(X)$
is open iff it is closed. This yields that
$c\in \mathbf {Baire}(X)$
is open iff it is closed. This yields that
![]() $\mathsf {S5}$
is sound with respect to
$\mathsf {S5}$
is sound with respect to
![]() $\mathbf {Baire}(X)$
for any topological space X. For completeness, we refine Hewitt’s [Reference Hewitt18] well-known concept of resolvability to that of Baire resolvability. A space is resolvable if it can be partitioned into two dense sets. Similarly, a closure algebra B is resolvable if there are
$\mathbf {Baire}(X)$
for any topological space X. For completeness, we refine Hewitt’s [Reference Hewitt18] well-known concept of resolvability to that of Baire resolvability. A space is resolvable if it can be partitioned into two dense sets. Similarly, a closure algebra B is resolvable if there are
![]() $a,b$
that are orthogonal (
$a,b$
that are orthogonal (
![]() $a\wedge b = 0$
) and dense (
$a\wedge b = 0$
) and dense (
![]() $\mathbf {c} a = \mathbf {c} b = 1$
). If we denote
$\mathbf {c} a = \mathbf {c} b = 1$
). If we denote
![]() $|\mathbb R|$
by
$|\mathbb R|$
by
![]() $\mathfrak c$
, we show that if X is crowded and either a complete metric space of cardinality
$\mathfrak c$
, we show that if X is crowded and either a complete metric space of cardinality
![]() $\mathfrak c$
or a locally compact Hausdorff space, then
$\mathfrak c$
or a locally compact Hausdorff space, then
![]() $\mathbf {Baire}(X)$
is resolvable. In fact, such algebras are
$\mathbf {Baire}(X)$
is resolvable. In fact, such algebras are
![]() $\mathfrak c$
-resolvable, meaning that we can find
$\mathfrak c$
-resolvable, meaning that we can find
![]() $\mathfrak c$
-many dense and pairwise orthogonal elements of
$\mathfrak c$
-many dense and pairwise orthogonal elements of
![]() $\mathbf {Baire}(X)$
. Our main tool in proving these results is the Disjoint Refinement Lemma (see, e.g., [Reference Comfort and Negrepontis10, Lemma 7.5]).
$\mathbf {Baire}(X)$
. Our main tool in proving these results is the Disjoint Refinement Lemma (see, e.g., [Reference Comfort and Negrepontis10, Lemma 7.5]).
Using these resolvability results we show that if X is a crowded, continuum-sized, complete metrizable space, then
![]() $\mathsf {S5}$
is strongly complete for
$\mathsf {S5}$
is strongly complete for
![]() $\mathbf {Baire}(X)$
, yielding a variant of the McKinsey–Tarski theorem for
$\mathbf {Baire}(X)$
, yielding a variant of the McKinsey–Tarski theorem for
![]() $\mathsf {S5}$
. In view of
$\mathsf {S5}$
. In view of
![]() $\mathfrak c$
-resolvability, strong completeness holds even if we extend the propositional language with continuum-many propositional variables. This yields a sharper version of strong completeness than that given in the literature, where only countable languages are typically considered. Some of our other main results include that every extension of
$\mathfrak c$
-resolvability, strong completeness holds even if we extend the propositional language with continuum-many propositional variables. This yields a sharper version of strong completeness than that given in the literature, where only countable languages are typically considered. Some of our other main results include that every extension of
![]() $\mathsf {S5}$
is the modal logic of some subalgebra of
$\mathsf {S5}$
is the modal logic of some subalgebra of
![]() $\mathbf {Baire}(X)$
for any crowded second-countable completely metrizable space X. These results also hold if we replace completely metrizable by locally compact Hausdorff. Finally, we show how to extend our results to the setting of the universal modality.
$\mathbf {Baire}(X)$
for any crowded second-countable completely metrizable space X. These results also hold if we replace completely metrizable by locally compact Hausdorff. Finally, we show how to extend our results to the setting of the universal modality.
2 Preliminaries
We assume some basic familiarity with Boolean algebras, topological spaces, and ordinal and cardinal arithmetic (see, e.g., [Reference Koppelberg19, Reference Engelking11, Reference Comfort and Negrepontis10]). In this section we will review closure algebras and their relation to modal logic.
2.1 Closure algebras
For each topological space X, the powerset
![]() $\wp (X)$
is a Boolean algebra and the closure operator
$\wp (X)$
is a Boolean algebra and the closure operator
![]() $\mathbf {c}:\wp (X)\to \wp (X)$
satisfies the Kuratowski axioms:
$\mathbf {c}:\wp (X)\to \wp (X)$
satisfies the Kuratowski axioms:
We call the pair
![]() $(\wp (X),\mathbf {c})$
the Kuratowski algebra of X and denote it by
$(\wp (X),\mathbf {c})$
the Kuratowski algebra of X and denote it by
![]() $\mathbf {Kur}(X)$
.
$\mathbf {Kur}(X)$
.
McKinsey and Tarski [Reference McKinsey and Tarski24] generalized the concept of a closure on
![]() $\wp (X)$
to that of a closure on an arbitrary Boolean algebra.
$\wp (X)$
to that of a closure on an arbitrary Boolean algebra.
Definition 2.1. A closure algebra is a pair
![]() $(B,\mathbf {c})$
, where B is a Boolean algebra and
$(B,\mathbf {c})$
, where B is a Boolean algebra and
![]() $\mathbf {c} \colon B \to B$
satisfies, for every
$\mathbf {c} \colon B \to B$
satisfies, for every
![]() $a,b\in B$
,
$a,b\in B$
,
-
1.
 $ a\le \mathbf {c} a$
,
$ a\le \mathbf {c} a$
, -
2.
 $\mathbf {c}\mathbf {c} a\le \mathbf {c} a$
,
$\mathbf {c}\mathbf {c} a\le \mathbf {c} a$
, -
3.
 $\mathbf {c}(a\vee b)=\mathbf {c} a\vee \mathbf {c} b, $
and
$\mathbf {c}(a\vee b)=\mathbf {c} a\vee \mathbf {c} b, $
and -
4.
 $\mathbf {c} 0=0$
.
$\mathbf {c} 0=0$
.
Let
![]() $\mathbf {i} a:= {-}\mathbf {c} {-}a$
. If
$\mathbf {i} a:= {-}\mathbf {c} {-}a$
. If
![]() $\mathbf {c}$
moreover satisfies
$\mathbf {c}$
moreover satisfies
then
![]() $(B,\mathbf {c})$
is a monadic algebra.
$(B,\mathbf {c})$
is a monadic algebra.
Remark 2.2. The notion of a monadic algebra is due to Halmos [Reference Halmos16].
As is the case for Boolean algebras, closure algebras can be represented as subalgebras of algebras based on a powerset.
Theorem 2.3 [Reference McKinsey and Tarski24, Theorem 2.4].
Each closure algebra is isomorphic to a subalgebra of the Kuratowski algebra
![]() $\mathbf {Kur}(X)$
of some topological space X.
$\mathbf {Kur}(X)$
of some topological space X.
Recall that Boolean algebras are partial orders
![]() $(B,{\leq })$
with a least element and a greatest element, usually denoted by
$(B,{\leq })$
with a least element and a greatest element, usually denoted by
![]() $0$
and
$0$
and
![]() $1$
, such that for
$1$
, such that for
![]() $a,b\in B$
their meet (greatest lower bound)
$a,b\in B$
their meet (greatest lower bound)
![]() $a\wedge b$
and complement
$a\wedge b$
and complement
![]() $-a$
are defined, and satisfy the usual axioms (see, e.g., [Reference Sikorski28, Reference Halmos17, Reference Koppelberg19]). If
$-a$
are defined, and satisfy the usual axioms (see, e.g., [Reference Sikorski28, Reference Halmos17, Reference Koppelberg19]). If
![]() $S\subseteq B$
, then
$S\subseteq B$
, then
![]() $\bigwedge S$
denotes its meet and
$\bigwedge S$
denotes its meet and
![]() $\bigvee S$
its join when they exist; the algebra B is complete provided these always exist. The next definition goes back to Halmos [Reference Halmos16].
$\bigvee S$
its join when they exist; the algebra B is complete provided these always exist. The next definition goes back to Halmos [Reference Halmos16].
Definition 2.4. We say that
![]() $A \subseteq B$
is relatively complete in B if for each
$A \subseteq B$
is relatively complete in B if for each
![]() $b\in B$
, the set
$b\in B$
, the set
![]() $ \{ a\in A \mid b\leq a \}$
has a least element (which then is
$ \{ a\in A \mid b\leq a \}$
has a least element (which then is
![]() $\bigwedge \{a\in A\mid b\le a\}$
).
$\bigwedge \{a\in A\mid b\le a\}$
).
Of particular importance are countable joins and meets, also called
![]() $\sigma $
-joins and
$\sigma $
-joins and
![]() $\sigma $
-meets; the algebra B is
$\sigma $
-meets; the algebra B is
![]() $\sigma $
-complete if such joins and meets always exist, in which case B is a
$\sigma $
-complete if such joins and meets always exist, in which case B is a
![]() $\sigma $
-algebra. An ideal is a set
$\sigma $
-algebra. An ideal is a set
![]() $\mathbf {I}\subseteq B$
which is closed under finite joins and with each element
$\mathbf {I}\subseteq B$
which is closed under finite joins and with each element
![]() $a\in \mathbf {I}$
also contains all elements underneath a; it is proper if
$a\in \mathbf {I}$
also contains all elements underneath a; it is proper if
![]() $1\notin \mathbf {I}$
; and it is a
$1\notin \mathbf {I}$
; and it is a
![]() $\sigma $
-ideal if it is closed under
$\sigma $
-ideal if it is closed under
![]() $\sigma $
-joins. For an ideal
$\sigma $
-joins. For an ideal
![]() $\mathbf {I}$
, recall that
$\mathbf {I}$
, recall that
![]() $B/\mathbf {I}$
is the set of equivalence classes of B under the equivalence relation given by
$B/\mathbf {I}$
is the set of equivalence classes of B under the equivalence relation given by
![]() $a\sim b$
if
$a\sim b$
if
![]() $a-b,b-a\in \mathbf {I}$
. We order
$a-b,b-a\in \mathbf {I}$
. We order
![]() $B/\mathbf {I}$
by
$B/\mathbf {I}$
by
![]() $[a] \leq [b]$
if
$[a] \leq [b]$
if
![]() $a-b\in \mathbf {I}$
. The quotient
$a-b\in \mathbf {I}$
. The quotient
![]() $B/\mathbf {I}$
is then a Boolean algebra; moreover, if B is
$B/\mathbf {I}$
is then a Boolean algebra; moreover, if B is
![]() $\sigma $
-complete and
$\sigma $
-complete and
![]() $\mathbf {I}$
is a
$\mathbf {I}$
is a
![]() $\sigma $
-ideal, then
$\sigma $
-ideal, then
![]() $B/\mathbf {I}$
is
$B/\mathbf {I}$
is
![]() $\sigma $
-complete (see, e.g., [Reference Halmos17, p. 56]).
$\sigma $
-complete (see, e.g., [Reference Halmos17, p. 56]).
2.2 Modal logic
We will work with the basic unimodal language as well as its extension with the universal modality. However, as we are interested in strong completeness for possibly uncountable sets of formulas, we want to allow for an arbitrary number of propositional variables. Given a cardinal
![]() $\lambda $
, let
$\lambda $
, let
![]() $\mathbb P^\lambda = \{p_\iota \mid \iota < \lambda \}$
be a set of
$\mathbb P^\lambda = \{p_\iota \mid \iota < \lambda \}$
be a set of
![]() $\lambda $
-many propositional variables. The modal language
$\lambda $
-many propositional variables. The modal language
![]() ${\mathcal L}^{\lambda }_{\Diamond \forall }$
is defined by the grammar (in Backus–Naur form)
${\mathcal L}^{\lambda }_{\Diamond \forall }$
is defined by the grammar (in Backus–Naur form)
where
![]() $p\in \mathbb P^\lambda $
. We also use standard shorthands, for example, defining
$p\in \mathbb P^\lambda $
. We also use standard shorthands, for example, defining
![]() $\bot $
as
$\bot $
as
![]() $p\wedge \neg p$
(where p is any fixed variable),
$p\wedge \neg p$
(where p is any fixed variable),
![]() $\varphi \vee \psi $
as
$\varphi \vee \psi $
as
![]() $\neg (\neg \varphi \wedge \neg \psi )$
, and
$\neg (\neg \varphi \wedge \neg \psi )$
, and
![]() $\Box \varphi $
as
$\Box \varphi $
as
![]() $\neg \Diamond \neg \varphi $
. We denote the
$\neg \Diamond \neg \varphi $
. We denote the
![]() $\forall $
-free fragment by
$\forall $
-free fragment by
![]() ${\mathcal L}^{\lambda }_{\Diamond }$
, and we omit the superscript
${\mathcal L}^{\lambda }_{\Diamond }$
, and we omit the superscript
![]() $\lambda $
when
$\lambda $
when
![]() $\lambda = \omega $
.
$\lambda = \omega $
.
We use
![]() $\Diamond $
as primitive rather than
$\Diamond $
as primitive rather than
![]() $\Box $
since, historically, algebraic semantics was presented in terms of closure-like operators on Boolean algebras. For our purposes, a logic is understood as a set of formulas closed under modus ponens, substitution, and necessitation. If
$\Box $
since, historically, algebraic semantics was presented in terms of closure-like operators on Boolean algebras. For our purposes, a logic is understood as a set of formulas closed under modus ponens, substitution, and necessitation. If
![]() $\Lambda $
is any logic over
$\Lambda $
is any logic over
![]() $\mathcal L$
, then
$\mathcal L$
, then
![]() $\Lambda ^\lambda $
denotes the least logic over
$\Lambda ^\lambda $
denotes the least logic over
![]() $\mathcal L^\lambda $
containing
$\mathcal L^\lambda $
containing
![]() $\Lambda \cap \mathcal L^\lambda $
.
$\Lambda \cap \mathcal L^\lambda $
.
We restrict our attention to logics above
![]() $\mathsf {S4}$
, and especially to
$\mathsf {S4}$
, and especially to
![]() $\mathsf {S5}$
and its extensions. A standard axiomatization of
$\mathsf {S5}$
and its extensions. A standard axiomatization of
![]() $\mathsf {S4}$
in
$\mathsf {S4}$
in
![]() ${\mathcal L}^{\lambda }_{\Diamond }$
(i.e., of
${\mathcal L}^{\lambda }_{\Diamond }$
(i.e., of
![]() $\mathsf {S4}^\lambda $
) is given by all (classical) propositional tautologies and the axioms and rules:
$\mathsf {S4}^\lambda $
) is given by all (classical) propositional tautologies and the axioms and rules:
 $$ \begin{align*} \begin{array}{ll} \mathbf{M:}\ \Diamond ( p \vee q) \to \Diamond p \vee \Diamond q \quad\quad & \quad\quad\mathbf{Sub:}\ \dfrac{\varphi(p_1,\dots,p_n)}{\varphi(\psi_1,\dots,\psi_n)}\\ \mathbf{T:}\ p \to \Diamond p & \\ \mathbf{4:}\ \Diamond \Diamond p \to \Diamond p \quad\quad & \quad\quad\mathbf{MP:}\ \dfrac{\varphi \ \ \varphi \to \psi}\psi\\ \mathbf{N:}\ \neg \Diamond \bot \quad\quad& \quad\quad \mathbf{Mon:}\ \dfrac{ \varphi \to \psi}{\Diamond \varphi \to \Diamond \psi}.\\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \mathbf{M:}\ \Diamond ( p \vee q) \to \Diamond p \vee \Diamond q \quad\quad & \quad\quad\mathbf{Sub:}\ \dfrac{\varphi(p_1,\dots,p_n)}{\varphi(\psi_1,\dots,\psi_n)}\\ \mathbf{T:}\ p \to \Diamond p & \\ \mathbf{4:}\ \Diamond \Diamond p \to \Diamond p \quad\quad & \quad\quad\mathbf{MP:}\ \dfrac{\varphi \ \ \varphi \to \psi}\psi\\ \mathbf{N:}\ \neg \Diamond \bot \quad\quad& \quad\quad \mathbf{Mon:}\ \dfrac{ \varphi \to \psi}{\Diamond \varphi \to \Diamond \psi}.\\ \end{array} \end{align*} $$
The logic
![]() $\mathsf {S5}^\lambda $
is then obtained by adding the axiom
$\mathsf {S5}^\lambda $
is then obtained by adding the axiom
-
5 :
 $\Diamond p \to \Box \Diamond p$
.
$\Diamond p \to \Box \Diamond p$
.
Given a logic
![]() $\Lambda $
over
$\Lambda $
over
![]() ${\mathcal L}^{\lambda }_{\Diamond }$
, we obtain a new logic
${\mathcal L}^{\lambda }_{\Diamond }$
, we obtain a new logic
![]() $\Lambda \mathsf {U}$
by adding the
$\Lambda \mathsf {U}$
by adding the
![]() $\mathsf {S5}$
axioms and rules for
$\mathsf {S5}$
axioms and rules for
![]() $ \forall $
(or rather for
$ \forall $
(or rather for
![]() $\exists :=\neg \forall \neg $
) and the connecting axiom
$\exists :=\neg \forall \neg $
) and the connecting axiom
![]() $\Diamond \varphi \to \exists \varphi $
. We will specifically be interested in
$\Diamond \varphi \to \exists \varphi $
. We will specifically be interested in
![]() $\mathsf {S5U}$
.
$\mathsf {S5U}$
.
The language
![]() ${\mathcal L}^{\lambda }_{\Diamond }$
has familiar Kripke semantics based on frames
${\mathcal L}^{\lambda }_{\Diamond }$
has familiar Kripke semantics based on frames
![]() $\mathfrak F = (W,R)$
, where
$\mathfrak F = (W,R)$
, where
![]() $W \neq \varnothing$
and
$W \neq \varnothing$
and
![]() $R \subseteq W\times W$
(see, e.g., [Reference Chagrov and Zakharyaschev7, Reference Blackburn, de Rijke and Venema6]). We will not review this semantics in detail, and instead regard it as a special case of topological or, more generally, algebraic semantics.
$R \subseteq W\times W$
(see, e.g., [Reference Chagrov and Zakharyaschev7, Reference Blackburn, de Rijke and Venema6]). We will not review this semantics in detail, and instead regard it as a special case of topological or, more generally, algebraic semantics.
Closure algebras provide the algebraic semantics for
![]() $\mathsf {S4}$
and its normal extensions, meaning those logics containing the axioms of
$\mathsf {S4}$
and its normal extensions, meaning those logics containing the axioms of
![]() $\mathsf {S4}$
and closed under the rules of
$\mathsf {S4}$
and closed under the rules of
![]() $\mathsf {S4}$
.
$\mathsf {S4}$
.
Definition 2.5. An algebraic model of
![]() $\mathsf {S4U}$
is a structure
$\mathsf {S4U}$
is a structure ![]() where B is a closure algebra and
where B is a closure algebra and ![]() is a valuation for
is a valuation for
![]() ${\mathcal L}^{\lambda }_{\Diamond \forall }$
; that is, a function such that
${\mathcal L}^{\lambda }_{\Diamond \forall }$
; that is, a function such that ![]() for each
for each
![]() $p \in \mathbb P^\lambda $
and
$p \in \mathbb P^\lambda $
and

We may also say that
![]() $\mathfrak M$
is an algebraic model of
$\mathfrak M$
is an algebraic model of
![]() $\mathsf {S4}$
, and that the restriction of
$\mathsf {S4}$
, and that the restriction of ![]() to
to
![]() ${\mathcal L}^{\lambda }_{\Diamond }$
is a valuation for
${\mathcal L}^{\lambda }_{\Diamond }$
is a valuation for
![]() ${\mathcal L}^{\lambda }_{\Diamond } $
.
${\mathcal L}^{\lambda }_{\Diamond } $
.
Validity, soundness, and completeness are then defined in the usual way:
Definition 2.6. Let ![]() be an algebraic model and
be an algebraic model and
![]() $\Gamma \cup \{\varphi \}\subseteq {\mathcal L}^{\lambda }_{\Diamond \forall }$
.
$\Gamma \cup \{\varphi \}\subseteq {\mathcal L}^{\lambda }_{\Diamond \forall }$
.
-
1. We say that
 $\varphi $
is valid in
$\varphi $
is valid in
 $\mathfrak M$
, written
$\mathfrak M$
, written
 $\mathfrak M\models \varphi $
, if
$\mathfrak M\models \varphi $
, if  . If
. If
 $\mathfrak M\models \gamma $
for each
$\mathfrak M\models \gamma $
for each
 $\gamma \in \Gamma $
, then we say that
$\gamma \in \Gamma $
, then we say that
 $\Gamma $
is valid in
$\Gamma $
is valid in
 $\mathfrak M$
and write
$\mathfrak M$
and write
 $\mathfrak M\models \Gamma $
.
$\mathfrak M\models \Gamma $
. -
2. We write
 $B \models \varphi $
if
$B \models \varphi $
if  for every valuation
for every valuation  on B, and define
on B, and define
 $B \models \Gamma $
similarly.
$B \models \Gamma $
similarly. -
3. If
 $\Omega $
is a class of closure algebras, we say that
$\Omega $
is a class of closure algebras, we say that
 $\varphi $
is valid in
$\varphi $
is valid in
 $\Omega $
provided
$\Omega $
provided
 $B \models \varphi $
for each
$B \models \varphi $
for each
 $B \in \Omega $
. That
$B \in \Omega $
. That
 $\Gamma $
is valid in
$\Gamma $
is valid in
 $\Omega $
is defined similarly.
$\Omega $
is defined similarly. -
4. For
 $S \subseteq \{\Diamond ,\forall \}$
, we denote the set of valid
$S \subseteq \{\Diamond ,\forall \}$
, we denote the set of valid
 ${\mathcal L}^{\lambda }_{S}$
-formulas in
${\mathcal L}^{\lambda }_{S}$
-formulas in
 $\Omega $
by
$\Omega $
by
 $\mathsf {Log}_S(\Omega )$
. If
$\mathsf {Log}_S(\Omega )$
. If
 $\Omega = \{ B \}$
, we simply write
$\Omega = \{ B \}$
, we simply write
 $\mathsf {Log}_S( B )$
.
$\mathsf {Log}_S( B )$
. -
5. A logic
 $\Lambda $
is sound for
$\Lambda $
is sound for
 $\Omega $
if
$\Omega $
if
 $ \Lambda \subseteq \mathsf {Log}_S(\Omega )$
, and complete if
$ \Lambda \subseteq \mathsf {Log}_S(\Omega )$
, and complete if
 $ \Lambda \supseteq \mathsf {Log}_S(\Omega )$
.
$ \Lambda \supseteq \mathsf {Log}_S(\Omega )$
.
We will also be interested in strong completeness of logics.
Definition 2.7. Let
![]() $\varphi $
be a formula,
$\varphi $
be a formula,
![]() $\Gamma $
a set of formulas, and
$\Gamma $
a set of formulas, and
![]() $\Lambda $
a logic in
$\Lambda $
a logic in
![]() ${\mathcal L}^{\lambda }_{\Diamond \forall }$
.
${\mathcal L}^{\lambda }_{\Diamond \forall }$
.
-
1. We write
 $\Gamma \vdash _\Lambda \varphi $
if there is a finite
$\Gamma \vdash _\Lambda \varphi $
if there is a finite
 $\Delta \subseteq \Gamma $
such that
$\Delta \subseteq \Gamma $
such that
 $(\forall \bigwedge \Delta ) \to \varphi \in \Lambda $
. We omit
$(\forall \bigwedge \Delta ) \to \varphi \in \Lambda $
. We omit
 $\Gamma $
when
$\Gamma $
when
 $\Gamma = \varnothing $
. If
$\Gamma = \varnothing $
. If
 $\Lambda $
is a logic in
$\Lambda $
is a logic in
 ${\mathcal L}^{\lambda }_{\Diamond }$
,
${\mathcal L}^{\lambda }_{\Diamond }$
,
 $\forall \bigwedge \Delta $
should be replaced by
$\forall \bigwedge \Delta $
should be replaced by
 $\Box \bigwedge \Delta $
.
$\Box \bigwedge \Delta $
. -
2. For a closure algebra B, we write
 $\Gamma \models _B\varphi $
if
$\Gamma \models _B\varphi $
if
 $B\models \Gamma $
implies
$B\models \Gamma $
implies
 $B\models \varphi $
.Footnote
2
$B\models \varphi $
.Footnote
2
-
3. We say that
 $\Lambda $
is strongly complete for a closure algebra B if
$\Lambda $
is strongly complete for a closure algebra B if
 $\Gamma \models _B\varphi $
implies
$\Gamma \models _B\varphi $
implies
 $\Gamma \vdash _\Lambda \varphi $
, and that
$\Gamma \vdash _\Lambda \varphi $
, and that
 $\Lambda $
is strongly complete for a class of structures
$\Lambda $
is strongly complete for a class of structures
 $\Omega $
if
$\Omega $
if
 $\Gamma \models _\Omega \varphi $
implies
$\Gamma \models _\Omega \varphi $
implies
 $\Gamma \vdash _\Lambda \varphi $
.
$\Gamma \vdash _\Lambda \varphi $
.
As we had mentioned previously, Kripke frames can be seen as a special case of Kuratowski algebras. If W is a set and
![]() $R\subseteq W\times W$
, then R induces an operator on
$R\subseteq W\times W$
, then R induces an operator on
![]() $\wp (W)$
given by
$\wp (W)$
given by
If W is nonempty and R reflexive and transitive, we say that
![]() $(W,R)$
is an
$(W,R)$
is an
![]() $\mathsf {S4}$
-frame. It is well known and not hard to check that in this case
$\mathsf {S4}$
-frame. It is well known and not hard to check that in this case
![]() $(\wp (W),R^{-1} )$
is a Kuratowski algebra, and that it is the Kuratowski algebra of the topology on W whose open sets are those
$(\wp (W),R^{-1} )$
is a Kuratowski algebra, and that it is the Kuratowski algebra of the topology on W whose open sets are those
![]() $U\subseteq W$
that satisfy
$U\subseteq W$
that satisfy
![]() $R(U) \subseteq U$
, recalling that
$R(U) \subseteq U$
, recalling that
If in addition R is symmetric, then we say that
![]() $(W,R)$
is an
$(W,R)$
is an
![]() $\mathsf {S5}$
-frame. We will tacitly identify an
$\mathsf {S5}$
-frame. We will tacitly identify an
![]() $\mathsf {S4}$
-frame with the associated topological space and even with the associated Kuratowski algebra.
$\mathsf {S4}$
-frame with the associated topological space and even with the associated Kuratowski algebra.
It is well known that the topologies arising from
![]() $\mathsf {S4}$
-frames are Alexandroff spaces; that is, topologies where arbitrary intersections of open sets are open. It is a consequence of the results of McKinsey and Tarski [Reference McKinsey and Tarski24] and Kripke [Reference Kripke21] that
$\mathsf {S4}$
-frames are Alexandroff spaces; that is, topologies where arbitrary intersections of open sets are open. It is a consequence of the results of McKinsey and Tarski [Reference McKinsey and Tarski24] and Kripke [Reference Kripke21] that
![]() $\mathsf {S4}$
is sound for the class of closure algebras, and complete for the class of
$\mathsf {S4}$
is sound for the class of closure algebras, and complete for the class of
![]() $\mathsf {S4}$
-frames. It is well known that
$\mathsf {S4}$
-frames. It is well known that
![]() $\mathsf {S4}$
and
$\mathsf {S4}$
and
![]() $\mathsf {S5}$
are strongly complete, with respect to both global and local consequence relations; both consequence relations are discussed in [Reference Blackburn, de Rijke and Venema6]; on the other hand, [Reference Rasiowa and Sikorski25] only focuses on the global consequence relation (using different terminology), which is the route we take here. The literature typically considers countable languages, but the adaptation of these results to uncountable languages is straightforward; we provide a sketch below.
$\mathsf {S5}$
are strongly complete, with respect to both global and local consequence relations; both consequence relations are discussed in [Reference Blackburn, de Rijke and Venema6]; on the other hand, [Reference Rasiowa and Sikorski25] only focuses on the global consequence relation (using different terminology), which is the route we take here. The literature typically considers countable languages, but the adaptation of these results to uncountable languages is straightforward; we provide a sketch below.
Theorem 2.8. For an infinite cardinal
![]() $\lambda $
, we have:
$\lambda $
, we have:
-
(1)
 $\mathsf {S4}^\lambda $
and
$\mathsf {S4}^\lambda $
and
 $\mathsf {S4U}^\lambda $
are strongly complete for the class of all
$\mathsf {S4U}^\lambda $
are strongly complete for the class of all
 $\mathsf {S4}$
-frames of cardinality at most
$\mathsf {S4}$
-frames of cardinality at most
 $\lambda $
.
$\lambda $
. -
(2)
 $\mathsf {S5}^\lambda $
and
$\mathsf {S5}^\lambda $
and
 $\mathsf {S5U}^\lambda $
are strongly complete for the class of all
$\mathsf {S5U}^\lambda $
are strongly complete for the class of all
 $\mathsf {S5}$
-frames of cardinality at most
$\mathsf {S5}$
-frames of cardinality at most
 $\lambda $
.
$\lambda $
.
Proof sketch
We outline how a standard proof, as given, e.g., in [Reference Blackburn, de Rijke and Venema6, p. 203], can be adapted to obtain the results as stated. Let
![]() $\Lambda $
be one of the logics mentioned above, and suppose that
$\Lambda $
be one of the logics mentioned above, and suppose that
![]() $\Gamma \not \vdash _{\Lambda } \varphi $
. The completeness proof by the relativized canonical model
$\Gamma \not \vdash _{\Lambda } \varphi $
. The completeness proof by the relativized canonical model ![]() , where
, where
![]() $W^\Gamma _c$
is the set of maximal consistent sets containing
$W^\Gamma _c$
is the set of maximal consistent sets containing
![]() $\Gamma $
, carries over mostly verbatim for uncountable languages. The relativized canonical model has the property that
$\Gamma $
, carries over mostly verbatim for uncountable languages. The relativized canonical model has the property that
![]() $\mathfrak M^\Gamma _c \models \Gamma $
and
$\mathfrak M^\Gamma _c \models \Gamma $
and
![]() $\mathfrak M^\Gamma _c \not \models \varphi $
. The only caveat is that the proof of the Lindenbaum lemma, that any consistent set of formulas
$\mathfrak M^\Gamma _c \not \models \varphi $
. The only caveat is that the proof of the Lindenbaum lemma, that any consistent set of formulas
![]() $\Delta $
can be extended to a maximal consistent set
$\Delta $
can be extended to a maximal consistent set
![]() $\Delta ' \supseteq \Delta $
, requires the use of Zorn’s lemma.
$\Delta ' \supseteq \Delta $
, requires the use of Zorn’s lemma.
The set of worlds
![]() $W^\Gamma _c$
may have cardinality greater than
$W^\Gamma _c$
may have cardinality greater than
![]() $\lambda $
. However, viewing
$\lambda $
. However, viewing
![]() ${\mathcal L}^{\lambda }_{\Diamond \forall }$
as a fragment of the first-order logic via the standard translation [Reference Blackburn, de Rijke and Venema6, p. 84], we may apply the downward Löwenheim–Skolem theorem to obtain a model
${\mathcal L}^{\lambda }_{\Diamond \forall }$
as a fragment of the first-order logic via the standard translation [Reference Blackburn, de Rijke and Venema6, p. 84], we may apply the downward Löwenheim–Skolem theorem to obtain a model
![]() $\mathfrak M$
of size at most
$\mathfrak M$
of size at most
![]() $\lambda $
such that
$\lambda $
such that
![]() $\mathfrak M \models \Gamma $
and
$\mathfrak M \models \Gamma $
and
![]() $\mathfrak M \not \models \varphi $
, as required.
$\mathfrak M \not \models \varphi $
, as required.
For a topological space X, it is well known (and not hard to see) that the following are equivalent:
-
1.
 $X\models \mathsf {S5}$
;
$X\models \mathsf {S5}$
; -
2. every open set of X is closed;
-
3. X has a basis which is also a partition of X;
-
4. X is an
 $\mathsf {S5}$
-frame.
$\mathsf {S5}$
-frame.
Thus, unlike the case of
![]() $\mathsf {S4}$
, no generality is achieved by passing to topological semantics of
$\mathsf {S4}$
, no generality is achieved by passing to topological semantics of
![]() $\mathsf {S5}$
. As we will see, the story is quite different for algebraic semantics.
$\mathsf {S5}$
. As we will see, the story is quite different for algebraic semantics.
We conclude this preliminary section by recalling the extensions of
![]() $\mathsf {S5}$
. For each natural number
$\mathsf {S5}$
. For each natural number
![]() $n>0$
, let
$n>0$
, let
 $$\begin{align*}\mathrm{Alt}_{n} := \bigwedge_{i = 1}^{n+1} \Diamond p_i \to \bigvee_{1\leq i<j\leq n+1} \Diamond(p_i\wedge p_j). \end{align*}$$
$$\begin{align*}\mathrm{Alt}_{n} := \bigwedge_{i = 1}^{n+1} \Diamond p_i \to \bigvee_{1\leq i<j\leq n+1} \Diamond(p_i\wedge p_j). \end{align*}$$
The logic
![]() $\mathsf {S5}_n$
is the extension of
$\mathsf {S5}_n$
is the extension of
![]() $\mathsf {S5}$
by the above axiom. We note that an
$\mathsf {S5}$
by the above axiom. We note that an
![]() $\mathsf {S5}$
-frame validates
$\mathsf {S5}$
-frame validates
![]() $\mathrm {Alt}_{n}$
iff each point has at most n distinct successors, or ‘alternatives’.
$\mathrm {Alt}_{n}$
iff each point has at most n distinct successors, or ‘alternatives’.
The next result is well known, and was originally proved by Scroggs [Reference Scroggs26]. We remark that in this article we use
![]() $\subset $
to denote strict inclusion.
$\subset $
to denote strict inclusion.
Theorem 2.9 (Scroggs’ Theorem).
The consistent extensions of
![]() $\mathsf {S5}$
form the following
$\mathsf {S5}$
form the following
![]() $(\omega +1)$
-chain (with respect to
$(\omega +1)$
-chain (with respect to
![]() $\supset ):$
$\supset ):$
Note that Scroggs’ Theorem applies to
![]() $\mathcal L^\lambda _\Diamond $
for any infinite
$\mathcal L^\lambda _\Diamond $
for any infinite
![]() $\lambda $
since any logic
$\lambda $
since any logic
![]() $\Lambda $
over
$\Lambda $
over
![]() $\mathcal L^\lambda _\Diamond $
is uniquely determined by
$\mathcal L^\lambda _\Diamond $
is uniquely determined by
![]() $ \Lambda \cap \mathcal L^\omega _\Diamond $
(as logics are closed under substitution). However, it is possible to exhibit infinite sets of formulas that may only be satisfied on uncountable models. For example, to satisfy
$ \Lambda \cap \mathcal L^\omega _\Diamond $
(as logics are closed under substitution). However, it is possible to exhibit infinite sets of formulas that may only be satisfied on uncountable models. For example, to satisfy
requires one point for each
![]() $p_\alpha $
.
$p_\alpha $
.
Definition 2.10. Let
![]() $(W,R)$
be an
$(W,R)$
be an
![]() $\mathsf {S5}$
-frame. Then it is a disjoint union of equivalence classes, or clusters,
$\mathsf {S5}$
-frame. Then it is a disjoint union of equivalence classes, or clusters,
![]() $\bigcup _{\iota < \kappa } C_\iota $
, where each
$\bigcup _{\iota < \kappa } C_\iota $
, where each
![]() $C_\iota $
is of the form
$C_\iota $
is of the form
![]() $R(\{w\})$
(which we henceforth write as
$R(\{w\})$
(which we henceforth write as
![]() $R(w)$
) for some
$R(w)$
) for some
![]() $w\in W$
. We define:
$w\in W$
. We define:
-
• the number of clusters to be
 $\kappa $
;
$\kappa $
; -
• the lower cluster size to be
 $\min _{\iota <\kappa }|C_\iota |$
, and
$\min _{\iota <\kappa }|C_\iota |$
, and -
• the upper cluster size to be
 $\sup _{\iota <\kappa } |C_\iota | $
.
$\sup _{\iota <\kappa } |C_\iota | $
.
The unique (up to isomorphism) frame with one cluster of size
![]() $\lambda $
is the
$\lambda $
is the
![]() $\lambda $
-cluster, and we denote it by
$\lambda $
-cluster, and we denote it by
![]() $\mathfrak C_\lambda $
.
$\mathfrak C_\lambda $
.
Theorem 2.8 can be sharpened using the structures
![]() $\mathfrak C_\lambda $
.
$\mathfrak C_\lambda $
.
Theorem 2.11. For each finite
![]() $n>0$
,
$n>0$
,
![]() $\mathsf {S5}_n$
is sound and strongly complete for the n-cluster, while for infinite
$\mathsf {S5}_n$
is sound and strongly complete for the n-cluster, while for infinite
![]() $\lambda $
,
$\lambda $
,
![]() $\mathsf {S5}^\lambda $
is sound and strongly complete for any
$\mathsf {S5}^\lambda $
is sound and strongly complete for any
![]() $\kappa $
-cluster with
$\kappa $
-cluster with
![]() $\kappa \ge \lambda $
.
$\kappa \ge \lambda $
.
Proof sketch
It follows from Scroggs’ Theorem that
![]() $\mathsf {S5}_n$
is sound and complete for the n-cluster. Strong completeness follows from compactness of the first-order logic (applied to the standard translations of the theorems of
$\mathsf {S5}_n$
is sound and complete for the n-cluster. Strong completeness follows from compactness of the first-order logic (applied to the standard translations of the theorems of
![]() $\mathsf {S5}_n$
) and using the formula stating that there are at most n elements. For infinite
$\mathsf {S5}_n$
) and using the formula stating that there are at most n elements. For infinite
![]() $\lambda $
, we have that
$\lambda $
, we have that
![]() $\mathsf {S5}^\lambda $
is sound and strongly complete for the class of
$\mathsf {S5}^\lambda $
is sound and strongly complete for the class of
![]() $\mathsf {S5}$
-frames. So, if
$\mathsf {S5}$
-frames. So, if
![]() $\Gamma \not \vdash \varphi $
, there is a model
$\Gamma \not \vdash \varphi $
, there is a model
![]() $\mathfrak M$
and a world w of
$\mathfrak M$
and a world w of
![]() $\mathfrak M$
such that
$\mathfrak M$
such that
![]() $\mathfrak M \models \Gamma $
but
$\mathfrak M \models \Gamma $
but ![]() . The submodel of
. The submodel of
![]() $\mathfrak M$
generated by w is the cluster
$\mathfrak M$
generated by w is the cluster
![]() $R(w)$
and satisfies the same formulas. We may assume that
$R(w)$
and satisfies the same formulas. We may assume that
![]() $R(w)$
is infinite by adding duplicates of a point if needed, which does not affect modal formulas. Then using the upwards or downwards Löwenheim–Skolem theorem, we can assume that this cluster is isomorphic to
$R(w)$
is infinite by adding duplicates of a point if needed, which does not affect modal formulas. Then using the upwards or downwards Löwenheim–Skolem theorem, we can assume that this cluster is isomorphic to
![]() $\mathfrak C_\kappa $
.
$\mathfrak C_\kappa $
.
3 Baire algebras as a new semantics for
 $\mathsf {S5}$
$\mathsf {S5}$
In this section we introduce the main concept of the paper, that of Baire algebras, which provide a new semantics for
![]() $\mathsf {S5}$
. Baire algebras are obtained from topological spaces X by modding out
$\mathsf {S5}$
. Baire algebras are obtained from topological spaces X by modding out
![]() $\wp (X)$
by the
$\wp (X)$
by the
![]() $\sigma $
-ideal
$\sigma $
-ideal
![]() $\mathbf {M}$
of meager subsets of X. We show that the closure operator
$\mathbf {M}$
of meager subsets of X. We show that the closure operator
![]() $\mathbf {c}$
on X gives rise to a closure operator on
$\mathbf {c}$
on X gives rise to a closure operator on
![]() $\wp ({X}) / \mathbf {M} $
, so that
$\wp ({X}) / \mathbf {M} $
, so that
![]() $(\wp ({X}) / \mathbf {M} ,\mathbf {c})$
is a monadic algebra.
$(\wp ({X}) / \mathbf {M} ,\mathbf {c})$
is a monadic algebra.
We start by the following well-known definition.
Definition 3.1. Let X be a topological space and
![]() $A \subseteq X$
.
$A \subseteq X$
.
-
1. A is nowhere dense if
 $\mathbf {i}\mathbf {c} A = \varnothing $
.
$\mathbf {i}\mathbf {c} A = \varnothing $
. -
2. A is meager if it is a
 $\sigma $
-union of nowhere dense sets.
$\sigma $
-union of nowhere dense sets. -
3.
 $\mathbf {M}$
denotes the set of meager subsets of X.
$\mathbf {M}$
denotes the set of meager subsets of X. -
4. X is a Baire space if for each nonempty open subset U of X, we have that
 $U \notin \mathbf {M}$
.
$U \notin \mathbf {M}$
.
It is easy to see that
![]() $\mathbf {M}$
is a
$\mathbf {M}$
is a
![]() $\sigma $
-ideal of
$\sigma $
-ideal of
![]() $\wp (X)$
. Therefore, the quotient
$\wp (X)$
. Therefore, the quotient
![]() $\wp ({X}) / \mathbf {M} $
is a
$\wp ({X}) / \mathbf {M} $
is a
![]() $\sigma $
-algebra (see, e.g., [Reference Halmos17, Section 13]). However,
$\sigma $
-algebra (see, e.g., [Reference Halmos17, Section 13]). However,
![]() $\wp ({X}) / \mathbf {M} $
is not always a complete Boolean algebra (see, e.g., [Reference Halmos17, Section 25]).
$\wp ({X}) / \mathbf {M} $
is not always a complete Boolean algebra (see, e.g., [Reference Halmos17, Section 25]).
We recall that elements of
![]() $\wp ({X}) / \mathbf {M} $
are equivalence classes of the equivalence relation given by
$\wp ({X}) / \mathbf {M} $
are equivalence classes of the equivalence relation given by
We write
![]() $[A]$
for the equivalence class of A under
$[A]$
for the equivalence class of A under
![]() $\approx $
. Then
$\approx $
. Then
![]() $[A]\sqsubseteq [B]$
iff
$[A]\sqsubseteq [B]$
iff
![]() $A\setminus B\in \mathbf {M}$
, and the operations on
$A\setminus B\in \mathbf {M}$
, and the operations on
![]() $\wp ({X}) / \mathbf {M} $
are given by
$\wp ({X}) / \mathbf {M} $
are given by

On the other hand, as we already pointed out above, if
![]() $S\subseteq \wp ({X}) / \mathbf {M} $
is uncountable, then
$S\subseteq \wp ({X}) / \mathbf {M} $
is uncountable, then ![]() may not always exist.
may not always exist.
Example 3.2.
-
1. Let
 $(W,R)$
be an
$(W,R)$
be an
 $\mathsf {S5}$
-frame, and identify it with the topological space whose opens are unions of equivalence classes of the equivalence relation R. For each
$\mathsf {S5}$
-frame, and identify it with the topological space whose opens are unions of equivalence classes of the equivalence relation R. For each
 $w\in W$
, since
$w\in W$
, since
 $R(w)$
is the least open containing w, which is also closed,
$R(w)$
is the least open containing w, which is also closed,
 $\varnothing $
is the only nowhere dense subset of W. Therefore,
$\varnothing $
is the only nowhere dense subset of W. Therefore,
 $\mathbf {M}=\{\varnothing \}$
, and so
$\mathbf {M}=\{\varnothing \}$
, and so
 $\wp (W)/\mathbf {M}$
is isomorphic to
$\wp (W)/\mathbf {M}$
is isomorphic to
 $\wp (W)$
.
$\wp (W)$
. -
2. More generally, if
 $(W,R)$
is an
$(W,R)$
is an
 $\mathsf {S4}$
-frame, a point
$\mathsf {S4}$
-frame, a point
 $w\in W$
is quasi-maximal if
$w\in W$
is quasi-maximal if
 $wRv$
implies
$wRv$
implies
 $vRw$
. Let
$vRw$
. Let
 $\mathsf {qmax}W$
be the set of quasi-maximal points. Then
$\mathsf {qmax}W$
be the set of quasi-maximal points. Then
 $w\in \mathsf {qmax}W$
iff
$w\in \mathsf {qmax}W$
iff
 $R(w) \subseteq R^{-1}(w)$
. Therefore,
$R(w) \subseteq R^{-1}(w)$
. Therefore,
 $w\in \mathsf {qmax}W$
iff
$w\in \mathsf {qmax}W$
iff
 $\{w\}$
is not nowhere dense. Thus, if W is countable,
$\{w\}$
is not nowhere dense. Thus, if W is countable,
 $\mathbf {M}=\{ A \subseteq W \mid A \subseteq W\setminus \mathsf {qmax}W \}$
, and hence
$\mathbf {M}=\{ A \subseteq W \mid A \subseteq W\setminus \mathsf {qmax}W \}$
, and hence
 $\wp (W)/\mathbf {M}$
is isomorphic to
$\wp (W)/\mathbf {M}$
is isomorphic to
 $\wp (\mathsf {qmax}W)$
(via
$\wp (\mathsf {qmax}W)$
(via
 $[A]\mapsto A\cap \mathsf {qmax}W$
).
$[A]\mapsto A\cap \mathsf {qmax}W$
).
Definition 3.3. Let X be a topological space.
-
1. We call
 $a\in \wp (X)/\mathbf {M}$
open if
$a\in \wp (X)/\mathbf {M}$
open if
 $a=[U]$
for some open
$a=[U]$
for some open
 $U\in \wp (X)$
, and closed if
$U\in \wp (X)$
, and closed if
 $a=[F]$
for some closed
$a=[F]$
for some closed
 $F\in \wp (X)$
. An element that is both open and closed is clopen.
$F\in \wp (X)$
. An element that is both open and closed is clopen. -
2. We denote the set of closed elements of
 $\wp (X)/\mathbf {M}$
by
$\wp (X)/\mathbf {M}$
by
 $\Gamma $
.
$\Gamma $
.
It is easy to see that
![]() $\Gamma $
is a bounded sublattice of
$\Gamma $
is a bounded sublattice of
![]() $\wp (X)/\mathbf {M}$
. We next show that
$\wp (X)/\mathbf {M}$
. We next show that
![]() $\Gamma $
is in fact a Boolean subalgebra of
$\Gamma $
is in fact a Boolean subalgebra of
![]() $\wp (X)/\mathbf {M}$
. For this we point out that if U is open, then
$\wp (X)/\mathbf {M}$
. For this we point out that if U is open, then
![]() $\mathbf {c} U\setminus U$
is nowhere dense (since it is closed and does not have any nonempty open subsets), so
$\mathbf {c} U\setminus U$
is nowhere dense (since it is closed and does not have any nonempty open subsets), so
![]() $[\mathbf {c} U] = [U]$
. Similarly, if F is closed, then
$[\mathbf {c} U] = [U]$
. Similarly, if F is closed, then
![]() $[F] = [\mathbf {i} F]$
.
$[F] = [\mathbf {i} F]$
.
Theorem 3.4. For every topological space X, we have that
![]() $\Gamma $
is a Boolean subalgebra of
$\Gamma $
is a Boolean subalgebra of
![]() $\wp ({X}) / \mathbf {M} $
.
$\wp ({X}) / \mathbf {M} $
.
Proof Since
![]() $\Gamma $
is a bounded sublattice of
$\Gamma $
is a bounded sublattice of
![]() $\wp ({X}) / \mathbf {M} $
, it is sufficient to show that
$\wp ({X}) / \mathbf {M} $
, it is sufficient to show that
![]() $a\in \Gamma $
implies
$a\in \Gamma $
implies
![]() $-a\in \Gamma $
. From
$-a\in \Gamma $
. From
![]() $a\in \Gamma $
it follows that
$a\in \Gamma $
it follows that
![]() $a=[F]$
for some F closed in X. Then
$a=[F]$
for some F closed in X. Then
![]() $-a=[X\setminus F]$
. Since
$-a=[X\setminus F]$
. Since
![]() $X\setminus F$
is open, we have that
$X\setminus F$
is open, we have that
![]() $X\setminus F \approx \mathbf {c}(X\setminus F)$
. Thus,
$X\setminus F \approx \mathbf {c}(X\setminus F)$
. Thus,
![]() $-a=[X\setminus F]=[\mathbf {c}(X\setminus F)]$
, and hence
$-a=[X\setminus F]=[\mathbf {c}(X\setminus F)]$
, and hence
![]() $-a\in \Gamma $
.
$-a\in \Gamma $
.
In fact,
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $\sigma $
-subalgebra of
$\sigma $
-subalgebra of
![]() $\wp (X)/\mathbf {M}$
, which follows from Equation (1) and the fact that intersection of closed sets is closed. But we can say more. For this we recall that a subset of X is a Borel set if it belongs to the
$\wp (X)/\mathbf {M}$
, which follows from Equation (1) and the fact that intersection of closed sets is closed. But we can say more. For this we recall that a subset of X is a Borel set if it belongs to the
![]() $\sigma $
-algebra generated by the open sets. We write
$\sigma $
-algebra generated by the open sets. We write
![]() $\mathbf {Borel}(X)$
for the
$\mathbf {Borel}(X)$
for the
![]() $\sigma $
-algebra of Borel sets and
$\sigma $
-algebra of Borel sets and
![]() $\mathbf {Borel}(X)/\mathbf {M}$
for the
$\mathbf {Borel}(X)/\mathbf {M}$
for the
![]() $\sigma $
-subalgebra of
$\sigma $
-subalgebra of
![]() $\wp (X)/\mathbf {M}$
isomorphic to
$\wp (X)/\mathbf {M}$
isomorphic to
![]() $\mathbf {Borel}(X)/(\mathbf {M}\cap \mathbf {Borel}(X))$
.
$\mathbf {Borel}(X)/(\mathbf {M}\cap \mathbf {Borel}(X))$
.
Theorem 3.5. For every topological space X, we have that
![]() $\Gamma =\mathbf {Borel}(X)/\mathbf {M}$
.
$\Gamma =\mathbf {Borel}(X)/\mathbf {M}$
.
Proof Since each closed set is Borel, we have
![]() $\Gamma \subseteq \mathbf {Borel}(X)/\mathbf {M}$
. For the reverse inclusion, every open set U is equivalent to its own closure, so
$\Gamma \subseteq \mathbf {Borel}(X)/\mathbf {M}$
. For the reverse inclusion, every open set U is equivalent to its own closure, so
![]() $[U]\in \Gamma $
. But
$[U]\in \Gamma $
. But
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $\sigma $
-algebra, so we conclude that
$\sigma $
-algebra, so we conclude that
![]() $\mathbf {Borel}(X)/\mathbf {M}\subseteq \Gamma $
, hence the equality.
$\mathbf {Borel}(X)/\mathbf {M}\subseteq \Gamma $
, hence the equality.
Since
![]() $\mathbf {Borel}(X)/\mathbf {M}$
is always a complete Boolean algebra (see [Reference Sikorski28, p. 75]), we obtain:
$\mathbf {Borel}(X)/\mathbf {M}$
is always a complete Boolean algebra (see [Reference Sikorski28, p. 75]), we obtain:
Corollary 3.6. For every topological space X, we have that
![]() $\Gamma $
is a complete Boolean algebra.
$\Gamma $
is a complete Boolean algebra.
In addition, we show that
![]() $\Gamma $
is a relatively complete subalgebra of
$\Gamma $
is a relatively complete subalgebra of
![]() $\wp (X)/\mathbf {M}$
:
$\wp (X)/\mathbf {M}$
:
Theorem 3.7. For an arbitrary topological space X, we have that
![]() $\Gamma $
is a relatively complete subalgebra of
$\Gamma $
is a relatively complete subalgebra of
![]() $\wp (X)/\mathbf {M}$
.
$\wp (X)/\mathbf {M}$
.
Proof Let
![]() $a = [A] \in \wp (X)/\mathbf {M} $
and let
$a = [A] \in \wp (X)/\mathbf {M} $
and let
![]() $\mathcal C_a $
be the collection of all closed sets C such that
$\mathcal C_a $
be the collection of all closed sets C such that
![]() $[A]\sqsubseteq [C]$
. By [Reference Sikorski28, p. 75],
$[A]\sqsubseteq [C]$
. By [Reference Sikorski28, p. 75], ![]() . Thus,
. Thus,
![]() $\mathcal C_a$
has a least element, and hence
$\mathcal C_a$
has a least element, and hence
![]() $\Gamma $
is a relatively complete subalgebra of
$\Gamma $
is a relatively complete subalgebra of
![]() $\wp (X)/\mathbf {M}$
.
$\wp (X)/\mathbf {M}$
.
Theorem 3.8. If X is a topological space, then
![]() $ \mathbf {Baire}(X) := (\wp ({X}) / \mathbf {M} ,\mathbf {c})$
is a monadic algebra, where for
$ \mathbf {Baire}(X) := (\wp ({X}) / \mathbf {M} ,\mathbf {c})$
is a monadic algebra, where for
![]() $a\in \wp ({X}) / \mathbf {M} $
,
$a\in \wp ({X}) / \mathbf {M} $
,
![]() $\mathbf {c} a$
is defined as the least closed element above a.
$\mathbf {c} a$
is defined as the least closed element above a.
Remark 3.9. In general, for a closure algebra
![]() $(B,\mathbf {c})$
, an element
$(B,\mathbf {c})$
, an element
![]() $a\in B$
is closed if
$a\in B$
is closed if
![]() $a = \mathbf {c} a$
, open if
$a = \mathbf {c} a$
, open if
![]() $a = \mathbf {i} a$
, and clopen if it is both closed and open. Since
$a = \mathbf {i} a$
, and clopen if it is both closed and open. Since
![]() $\mathbf {Baire}(X)$
is a closure algebra, it is not hard to check that these notions coincide with the ones given in Definition 3.3.
$\mathbf {Baire}(X)$
is a closure algebra, it is not hard to check that these notions coincide with the ones given in Definition 3.3.
4 Baire resolvability
To obtain completeness results with respect to this new semantics we require to introduce the concept of Baire resolvability, which refines the concept of resolvability introduced by Hewitt [Reference Hewitt18]. A space is resolvable if it can be partitioned into two disjoint dense sets. This notion readily extends to the algebraic setting:
Definition 4.1. Let B be a Boolean algebra. We call
![]() $a,b\in B$
orthogonal if
$a,b\in B$
orthogonal if
![]() $a\wedge b=0$
, and a family
$a\wedge b=0$
, and a family
![]() $\{a_i\mid i\in I\}$
pairwise orthogonal if
$\{a_i\mid i\in I\}$
pairwise orthogonal if
![]() $a_i\wedge a_j=0$
for
$a_i\wedge a_j=0$
for
![]() $i\ne j$
.
$i\ne j$
.
Definition 4.2. Let
![]() $(B,\mathbf {c})$
be a closure algebra and
$(B,\mathbf {c})$
be a closure algebra and
![]() $\kappa $
a nonzero cardinal.
$\kappa $
a nonzero cardinal.
-
1. We call
 $a\in B$
dense if
$a\in B$
dense if
 $\mathbf {c} a=1$
.
$\mathbf {c} a=1$
. -
2. We call
 $(B,\mathbf {c})\ \kappa $
-resolvable if there is a pairwise orthogonal family of dense elements whose cardinality is
$(B,\mathbf {c})\ \kappa $
-resolvable if there is a pairwise orthogonal family of dense elements whose cardinality is
 $\kappa $
.
$\kappa $
.
Definition 4.3. Let
![]() $(B,\mathbf {c})$
be a closure algebra,
$(B,\mathbf {c})$
be a closure algebra,
![]() $a\in B$
, and
$a\in B$
, and
![]() $\kappa $
a nonzero cardinal. We call
$\kappa $
a nonzero cardinal. We call
![]() $a\ \kappa $
-resolvable if there is a pairwise orthogonal family
$a\ \kappa $
-resolvable if there is a pairwise orthogonal family
![]() $\mathcal R = \{b_\iota \mid \iota <\kappa \}$
such that
$\mathcal R = \{b_\iota \mid \iota <\kappa \}$
such that
![]() $b_\iota \leq a$
and
$b_\iota \leq a$
and
![]() $a\le \mathbf {c} b_\iota $
for each
$a\le \mathbf {c} b_\iota $
for each
![]() $\iota <\kappa $
. The family
$\iota <\kappa $
. The family
![]() $\mathcal R$
is a
$\mathcal R$
is a
![]() $\kappa $
-resolution of a.
$\kappa $
-resolution of a.
If
![]() $\{[A_\iota ] \mid \iota <\kappa \}$
is a
$\{[A_\iota ] \mid \iota <\kappa \}$
is a
![]() $\kappa $
-resolution of
$\kappa $
-resolution of
![]() $\mathbf {Baire}(X)$
, we remark that the collection of representatives
$\mathbf {Baire}(X)$
, we remark that the collection of representatives
![]() $A_\iota $
need not come from a partition of X; for example, two of them may have nonempty (but meager) intersection. However, sometimes it will be useful to have ‘nice’ representatives, as made precise in the following definition.
$A_\iota $
need not come from a partition of X; for example, two of them may have nonempty (but meager) intersection. However, sometimes it will be useful to have ‘nice’ representatives, as made precise in the following definition.
Definition 4.4. Let X be a Baire space and let
![]() $Y\subseteq X$
. If
$Y\subseteq X$
. If
![]() $A\subseteq Y$
is such that
$A\subseteq Y$
is such that
![]() $[Y]\sqsubseteq \mathbf {c}[A]$
, we say that A is Baire-dense in
$[Y]\sqsubseteq \mathbf {c}[A]$
, we say that A is Baire-dense in
![]() $Y.$
For a nonzero cardinal
$Y.$
For a nonzero cardinal
![]() $\kappa $
, we call
$\kappa $
, we call
![]() $Y \subseteq X$
Baire
$Y \subseteq X$
Baire
![]() $\kappa $
-resolvable if there is a partition
$\kappa $
-resolvable if there is a partition
![]() $\{A_\iota \mid \iota <\kappa \}$
of Y such that, for each
$\{A_\iota \mid \iota <\kappa \}$
of Y such that, for each
![]() $\iota $
,
$\iota $
,
![]() $ A_\iota $
is Baire-dense in Y. We call
$ A_\iota $
is Baire-dense in Y. We call
![]() $\{A_\iota \mid \iota <\kappa \}$
a Baire
$\{A_\iota \mid \iota <\kappa \}$
a Baire
![]() $\kappa $
-resolution of Y.
$\kappa $
-resolution of Y.
If
![]() $\{A_\iota \mid \iota <\kappa \}$
is a Baire
$\{A_\iota \mid \iota <\kappa \}$
is a Baire
![]() $\kappa $
-resolution of Y, then
$\kappa $
-resolution of Y, then
![]() $\{ [A_\iota ] \mid \iota <\kappa \}$
is a
$\{ [A_\iota ] \mid \iota <\kappa \}$
is a
![]() $\kappa $
-resolution of
$\kappa $
-resolution of
![]() $[Y]$
. Thus, Baire
$[Y]$
. Thus, Baire
![]() $\kappa $
-resolvability of Y implies
$\kappa $
-resolvability of Y implies
![]() $\kappa $
-resolvability of
$\kappa $
-resolvability of
![]() $[Y]$
. As we have mentioned, the converse is not true a priori since the
$[Y]$
. As we have mentioned, the converse is not true a priori since the
![]() $A_\iota $
do not have to form a partition, but it is not hard to check that the two notions are equivalent if
$A_\iota $
do not have to form a partition, but it is not hard to check that the two notions are equivalent if
![]() $\kappa $
is countable: just define recursively
$\kappa $
is countable: just define recursively
![]() $A^{\prime }_0=A_0$
and
$A^{\prime }_0=A_0$
and
![]() $A^{\prime }_{i+1} = A_{i+1}\setminus \bigcup _{j<i}A^{\prime }_j$
. Note that
$A^{\prime }_{i+1} = A_{i+1}\setminus \bigcup _{j<i}A^{\prime }_j$
. Note that
![]() $a_\iota =[A_\iota ]$
is dense in
$a_\iota =[A_\iota ]$
is dense in
![]() $\mathbf {Baire}(X)$
provided for each nonempty open
$\mathbf {Baire}(X)$
provided for each nonempty open
![]() $U\in \wp (X)$
we have
$U\in \wp (X)$
we have
![]() $A_\iota \cap U \notin \mathbf {M}$
. We call such sets ‘nowhere meager’. More generally, we adopt the following conventions.
$A_\iota \cap U \notin \mathbf {M}$
. We call such sets ‘nowhere meager’. More generally, we adopt the following conventions.
Definition 4.5. Let X be a topological space and
![]() $\kappa $
a cardinal. We say that:
$\kappa $
a cardinal. We say that:
-
•
 $A\subseteq X$
is nowhere meager if for each nonempty open
$A\subseteq X$
is nowhere meager if for each nonempty open
 $U \subseteq X$
we have that
$U \subseteq X$
we have that
 $A \cap U \notin \mathbf {M}$
.
$A \cap U \notin \mathbf {M}$
. -
•
 $A\subseteq X$
is somewhere meager if it is not nowhere meager.
$A\subseteq X$
is somewhere meager if it is not nowhere meager. -
• X is everywhere Baire
 $\kappa $
-resolvable if each open
$\kappa $
-resolvable if each open
 $U\subseteq X$
is Baire
$U\subseteq X$
is Baire
 $\kappa $
-resolvable (seen as a subspace of X).
$\kappa $
-resolvable (seen as a subspace of X). -
• X is somewhere Baire
 $\kappa $
-resolvable if there is some nonempty open
$\kappa $
-resolvable if there is some nonempty open
 $U\subseteq X$
that is Baire
$U\subseteq X$
that is Baire
 $\kappa $
-resolvable.
$\kappa $
-resolvable. -
• X is nowhere Baire
 $\kappa $
-resolvable if it is not somewhere Baire
$\kappa $
-resolvable if it is not somewhere Baire
 $\kappa $
-resolvable.
$\kappa $
-resolvable.
So,
![]() $A\subseteq X$
is somewhere meager provided that there is a nonempty open
$A\subseteq X$
is somewhere meager provided that there is a nonempty open
![]() $U\subseteq X$
with
$U\subseteq X$
with
![]() $A\cap U\in \mathbf {M}$
. We have the following characterization of Baire resolvability:
$A\cap U\in \mathbf {M}$
. We have the following characterization of Baire resolvability:
Lemma 4.6. Let X be a Baire space and
![]() $\kappa $
a nonzero cardinal. Then X is Baire
$\kappa $
a nonzero cardinal. Then X is Baire
![]() $\kappa $
-resolvable iff it is everywhere Baire
$\kappa $
-resolvable iff it is everywhere Baire
![]() $\kappa $
-resolvable.
$\kappa $
-resolvable.
Proof Clearly if X is everywhere Baire
![]() $\kappa $
-resolvable, then X is Baire
$\kappa $
-resolvable, then X is Baire
![]() $\kappa $
-resolvable. Conversely, suppose that X is Baire
$\kappa $
-resolvable. Conversely, suppose that X is Baire
![]() $\kappa $
-resolvable and
$\kappa $
-resolvable and
![]() $\{A_\iota \mid \iota <\kappa \}$
is a Baire
$\{A_\iota \mid \iota <\kappa \}$
is a Baire
![]() $\kappa $
-resolution of X. Let
$\kappa $
-resolution of X. Let
![]() $U \subseteq X$
be nonempty open. Since
$U \subseteq X$
be nonempty open. Since
![]() $A_\iota $
is nowhere meager,
$A_\iota $
is nowhere meager,
![]() $A_\iota \cap U$
is nowhere meager in U. Thus,
$A_\iota \cap U$
is nowhere meager in U. Thus,
![]() $\{A_\iota \cap U\mid \iota <\kappa \}$
is a Baire
$\{A_\iota \cap U\mid \iota <\kappa \}$
is a Baire
![]() $\kappa $
-resolution of U.
$\kappa $
-resolution of U.
Let X be a Baire space and
![]() $\kappa \le \omega $
. If X is Baire
$\kappa \le \omega $
. If X is Baire
![]() $\kappa $
-resolvable, then X is
$\kappa $
-resolvable, then X is
![]() $\kappa $
-resolvable, given that Baire-dense sets must be dense. The next example shows that the converse is not true in general.
$\kappa $
-resolvable, given that Baire-dense sets must be dense. The next example shows that the converse is not true in general.
Example 4.7. Let
![]() $X = \omega +1$
with the topology whose nonempty open sets are of the form
$X = \omega +1$
with the topology whose nonempty open sets are of the form
![]() $[n,\omega ]$
where
$[n,\omega ]$
where
![]() $n<\omega $
. Then
$n<\omega $
. Then
![]() $\{\omega \}$
is dense in X, and being a singleton, it cannot be written as a countable union of nowhere dense sets, so
$\{\omega \}$
is dense in X, and being a singleton, it cannot be written as a countable union of nowhere dense sets, so
![]() $\{\omega \}\notin \mathbf {M}$
. Therefore, every nonempty open set in X is not meager, and hence X is a Baire space.
$\{\omega \}\notin \mathbf {M}$
. Therefore, every nonempty open set in X is not meager, and hence X is a Baire space.
Each infinite subset of
![]() $[0,\omega )$
is dense. Therefore, if we write
$[0,\omega )$
is dense. Therefore, if we write
![]() $[0,\omega )$
as a countable union of infinite disjoint subsets of
$[0,\omega )$
as a countable union of infinite disjoint subsets of
![]() $[0,\omega )$
, we obtain that X is
$[0,\omega )$
, we obtain that X is
![]() $\omega $
-resolvable. On the other hand,
$\omega $
-resolvable. On the other hand,
![]() $[0,\omega )=\bigcup _{n<\omega }[0,n]$
and each
$[0,\omega )=\bigcup _{n<\omega }[0,n]$
and each
![]() $[0,n]$
is nowhere dense, so
$[0,n]$
is nowhere dense, so
![]() $[0,\omega )\in \mathbf {M}$
. Thus, no subset of
$[0,\omega )\in \mathbf {M}$
. Thus, no subset of
![]() $[0,\omega )$
is nowhere meager, yielding that X is not Baire 2-resolvable.
$[0,\omega )$
is nowhere meager, yielding that X is not Baire 2-resolvable.
As we pointed out in the Introduction, our main Baire resolvability results follow from the Disjoint Refinement Lemma (see [Reference Comfort and Negrepontis10, Lemma 7.5] and [Reference Comfort and Negrepontis10, Notes for Section 7] for the history of this result). This lemma has been used in proofs of resolvability in other contexts (see, e.g., [Reference Comfort and García-Ferreira9]); ours follows a similar pattern.
Lemma 4.8 (Disjoint Refinement Lemma).
Let
![]() $\kappa $
be an infinite cardinal and
$\kappa $
be an infinite cardinal and
![]() $\{ A_\iota \mid \iota <\kappa \}$
a family of sets such that
$\{ A_\iota \mid \iota <\kappa \}$
a family of sets such that
![]() $|A_\iota |=\kappa $
for each
$|A_\iota |=\kappa $
for each
![]() $\iota <\kappa $
. Then there is a family
$\iota <\kappa $
. Then there is a family
![]() $\{ B_\iota \mid \iota <\kappa \}$
of pairwise disjoint sets such that
$\{ B_\iota \mid \iota <\kappa \}$
of pairwise disjoint sets such that
![]() $B_\iota \subseteq A_\iota $
and
$B_\iota \subseteq A_\iota $
and
![]() $|B_\iota |=\kappa $
for each
$|B_\iota |=\kappa $
for each
![]() $\iota <\kappa $
.
$\iota <\kappa $
.
We will use the following version of the Disjoint Refinement Lemma:
Lemma 4.9. Let
![]() $\kappa $
be an infinite cardinal, X a set, and
$\kappa $
be an infinite cardinal, X a set, and
![]() $\mathcal K$
a family of subsets of X such that
$\mathcal K$
a family of subsets of X such that
![]() $|\mathcal K| \leq \kappa $
and
$|\mathcal K| \leq \kappa $
and
![]() $|K| \geq \kappa $
for each
$|K| \geq \kappa $
for each
![]() $K\in \mathcal K$
. Then there is a partition
$K\in \mathcal K$
. Then there is a partition
![]() $\{ A_\iota \mid \iota < \kappa \}$
of X such that
$\{ A_\iota \mid \iota < \kappa \}$
of X such that
![]() $ A_\iota \cap K \neq \varnothing $
for each
$ A_\iota \cap K \neq \varnothing $
for each
![]() $K\in \mathcal K$
and
$K\in \mathcal K$
and
![]() $\iota < \kappa $
.
$\iota < \kappa $
.
Proof Enumerate
![]() $\mathcal K$
as
$\mathcal K$
as
![]() $\{ K_\iota \mid \iota <\kappa \}$
, and for each
$\{ K_\iota \mid \iota <\kappa \}$
, and for each
![]() $\iota <\kappa $
let
$\iota <\kappa $
let
![]() $K^{\prime }_\iota $
be a subset of
$K^{\prime }_\iota $
be a subset of
![]() $K_\iota $
with
$K_\iota $
with
![]() $|K^{\prime }_\iota | = \kappa $
. By the Disjoint Refinement Lemma, there is a family
$|K^{\prime }_\iota | = \kappa $
. By the Disjoint Refinement Lemma, there is a family
![]() $\{ B_\iota \mid \iota <\kappa \}$
of pairwise disjoint sets such that
$\{ B_\iota \mid \iota <\kappa \}$
of pairwise disjoint sets such that
![]() $B_\iota \subseteq K^{\prime }_\iota $
and
$B_\iota \subseteq K^{\prime }_\iota $
and
![]() $|B_\iota |=\kappa $
for each
$|B_\iota |=\kappa $
for each
![]() $\iota <\kappa $
. Enumerating each
$\iota <\kappa $
. Enumerating each
![]() $B_\iota $
as
$B_\iota $
as
![]() $\{b_{\iota \nu }\mid \nu <\kappa \}$
, for
$\{b_{\iota \nu }\mid \nu <\kappa \}$
, for
![]() $\nu <\kappa $
, let
$\nu <\kappa $
, let
![]() $A^{\prime }_\nu = \{b_{\iota \nu }\mid \iota <\kappa \}$
. To ensure that we obtain a partition, let
$A^{\prime }_\nu = \{b_{\iota \nu }\mid \iota <\kappa \}$
. To ensure that we obtain a partition, let
![]() $A_0 = A^{\prime }_0\cup \left ( X \setminus \bigcup _{\nu <\kappa } A^{\prime }_\nu \right )$
and for
$A_0 = A^{\prime }_0\cup \left ( X \setminus \bigcup _{\nu <\kappa } A^{\prime }_\nu \right )$
and for
![]() $\nu>0$
, let
$\nu>0$
, let
![]() $A_\nu = A^{\prime }_\nu $
. Then
$A_\nu = A^{\prime }_\nu $
. Then
![]() $\{ A_\nu \mid \nu <\kappa \}$
is the desired partition, since for each
$\{ A_\nu \mid \nu <\kappa \}$
is the desired partition, since for each
![]() $\iota <\kappa $
we have that
$\iota <\kappa $
we have that
![]() $b_{\iota \nu } \in A_\nu \cap K^{\prime }_\iota \subseteq A_\nu \cap K_\iota $
.
$b_{\iota \nu } \in A_\nu \cap K^{\prime }_\iota \subseteq A_\nu \cap K_\iota $
.
To apply Lemma 4.9 to Baire resolvability, we use the notion of a
![]() $\kappa $
-witnessing family.
$\kappa $
-witnessing family.
Definition 4.10. Let X be a Baire space and
![]() $\kappa $
a cardinal. We call
$\kappa $
a cardinal. We call
![]() $\mathcal K \subseteq \wp (X)$
a
$\mathcal K \subseteq \wp (X)$
a
![]() $\kappa $
-witnessing family for X provided
$\kappa $
-witnessing family for X provided
![]() $|\mathcal K|\leq \kappa $
,
$|\mathcal K|\leq \kappa $
,
![]() $|K| \geq \kappa $
for each
$|K| \geq \kappa $
for each
![]() $K\in \mathcal K$
, and if
$K\in \mathcal K$
, and if
![]() $A\subseteq X$
is somewhere meager, then there is
$A\subseteq X$
is somewhere meager, then there is
![]() $K\in \mathcal K$
with
$K\in \mathcal K$
with
![]() $K\cap A = \varnothing $
.
$K\cap A = \varnothing $
.
Theorem 4.11. Let
![]() $\kappa $
be an infinite cardinal. Each Baire space that has a
$\kappa $
be an infinite cardinal. Each Baire space that has a
![]() $\kappa $
-witnessing family is Baire
$\kappa $
-witnessing family is Baire
![]() $\kappa $
-resolvable.
$\kappa $
-resolvable.
Proof Let X be a Baire space with a
![]() $\kappa $
-witnessing family
$\kappa $
-witnessing family
![]() $\mathcal K$
. By Lemma 4.9, there is a family
$\mathcal K$
. By Lemma 4.9, there is a family
![]() $\{ A_\iota \mid \iota <\kappa \}$
of pairwise disjoint subsets of X such that
$\{ A_\iota \mid \iota <\kappa \}$
of pairwise disjoint subsets of X such that
![]() $ A_\iota \cap K \neq \varnothing $
for each
$ A_\iota \cap K \neq \varnothing $
for each
![]() $K\in \mathcal K$
and
$K\in \mathcal K$
and
![]() $\iota <\kappa $
. We claim that each
$\iota <\kappa $
. We claim that each
![]() $A_\iota $
is nowhere meager. Otherwise, since
$A_\iota $
is nowhere meager. Otherwise, since
![]() $\mathcal K$
is a
$\mathcal K$
is a
![]() $\kappa $
-witnessing family, there is
$\kappa $
-witnessing family, there is
![]() $K\in \mathcal K$
such that
$K\in \mathcal K$
such that
![]() $K\cap A_\iota =\varnothing $
, a contradiction. Thus,
$K\cap A_\iota =\varnothing $
, a contradiction. Thus,
![]() $\{ A_\iota \mid \iota <\kappa \}$
gives the desired Baire
$\{ A_\iota \mid \iota <\kappa \}$
gives the desired Baire
![]() $\kappa $
-resolution of X.
$\kappa $
-resolution of X.
In the next two lemmas we show that the uncountable compact sets provide a witnessing family in many Baire spaces. These lemmas are folklore, but we state them in the precise form we need and briefly recall their proofs.
Lemma 4.12. Let X be a crowded topological space which is either locally compact Hausdorff or completely metrizable. If
![]() $A\subseteq X$
is somewhere meager, then there is a compact
$A\subseteq X$
is somewhere meager, then there is a compact
![]() $K\subseteq X$
such that
$K\subseteq X$
such that
![]() $|K|\geq \mathfrak c$
and
$|K|\geq \mathfrak c$
and
![]() $A\cap K=\varnothing $
.
$A\cap K=\varnothing $
.
Proof The proof follows the standard tree construction method (see, e.g., [Reference Engelking11, Exercise 3.12.11]). We provide a sketch in the case when X is a crowded locally compact Hausdorff space. Suppose that
![]() $A\subseteq X$
is somewhere meager, so there is a nonempty open
$A\subseteq X$
is somewhere meager, so there is a nonempty open
![]() $U\subseteq X$
such that
$U\subseteq X$
such that
![]() $A\cap U\in \mathbf {M}$
. Then
$A\cap U\in \mathbf {M}$
. Then
![]() $A\cap U=\bigcup _{n<\omega } B_n$
, with each
$A\cap U=\bigcup _{n<\omega } B_n$
, with each
![]() $B_n$
nowhere dense. Using the assumption that X is crowded locally compact Hausdorff, to each finite sequence
$B_n$
nowhere dense. Using the assumption that X is crowded locally compact Hausdorff, to each finite sequence ![]() , we can assign a compact set
, we can assign a compact set
![]() $K_{\mathbf {b}} \subseteq U$
so that:
$K_{\mathbf {b}} \subseteq U$
so that:
-
•
 $K_{\mathbf {b}}$
has nonempty interior;
$K_{\mathbf {b}}$
has nonempty interior; -
•
 $B_i \cap K_{\mathbf {b}} = \varnothing $
for each
$B_i \cap K_{\mathbf {b}} = \varnothing $
for each
 $i\leq n$
;
$i\leq n$
; -
• if
 $\mathbf {b}$
is an initial segment of
$\mathbf {b}$
is an initial segment of
 $\mathbf {b}'$
, then
$\mathbf {b}'$
, then
 $K_{\mathbf {b}'} \subseteq K_{\mathbf {b}}$
;
$K_{\mathbf {b}'} \subseteq K_{\mathbf {b}}$
; -
• if
 $\mathbf {b}$
,
$\mathbf {b}$
,
 $\mathbf {b}'$
are incomparable (i.e., disagree on some coordinate), then
$\mathbf {b}'$
are incomparable (i.e., disagree on some coordinate), then
 $K_{\mathbf {b}} \cap K_{\mathbf {b}'} = \varnothing $
.
$K_{\mathbf {b}} \cap K_{\mathbf {b}'} = \varnothing $
.
Let
![]() $K = \bigcap _{n <\omega } \bigcup _{|\mathbf {b}| = n} K_{\mathbf {b}}.$
Being an intersection of compact sets, this is a compact set. It follows from the construction that each
$K = \bigcap _{n <\omega } \bigcup _{|\mathbf {b}| = n} K_{\mathbf {b}}.$
Being an intersection of compact sets, this is a compact set. It follows from the construction that each
![]() $K_{\mathbf {b}}$
is contained in U and that
$K_{\mathbf {b}}$
is contained in U and that
![]() $A\cap K=\varnothing $
. The intersections along infinite sequences
$A\cap K=\varnothing $
. The intersections along infinite sequences
![]() $\mathbf {b} \in \{0,1\}^{\omega }$
are nonempty and disjoint, witnessing that
$\mathbf {b} \in \{0,1\}^{\omega }$
are nonempty and disjoint, witnessing that
![]() $|K| \geq \mathfrak c$
.
$|K| \geq \mathfrak c$
.
The proof for a crowded completely metrizable X is essentially the same, but we let each
![]() $K_{\mathbf {b}}$
be a ball of radius at most
$K_{\mathbf {b}}$
be a ball of radius at most
![]() $2^{-|\mathbf {b}|}$
so that we can use that X is complete.
$2^{-|\mathbf {b}|}$
so that we can use that X is complete.
Lemma 4.13. Let X be either Hausdorff and second-countable or metrizable and of cardinality continuum. Then X contains at most
![]() $\mathfrak c$
compact sets.
$\mathfrak c$
compact sets.
Proof First suppose that X is Hausdorff and second-countable. The latter implies that X contains at most
![]() $\mathfrak c$
open sets, and so at most
$\mathfrak c$
open sets, and so at most
![]() $\mathfrak c$
closed sets. Since X is Hausdorff, compact sets are closed, and hence there can be at most
$\mathfrak c$
closed sets. Since X is Hausdorff, compact sets are closed, and hence there can be at most
![]() $\mathfrak c$
compact sets.
$\mathfrak c$
compact sets.
Next suppose that X is metrizable and of cardinality continuum. Then every compact set
![]() $K\subseteq X$
is the closure of some countable subset of X (see, e.g., [Reference Engelking11, Theorem 4.1.18]). Since X has
$K\subseteq X$
is the closure of some countable subset of X (see, e.g., [Reference Engelking11, Theorem 4.1.18]). Since X has
![]() $\mathfrak c$
-many countable subsets, there can be at most
$\mathfrak c$
-many countable subsets, there can be at most
![]() $\mathfrak c$
values for K.
$\mathfrak c$
values for K.
Putting together these results, we arrive at the following:
Theorem 4.14. Suppose that X is a crowded space which is either locally compact, Hausdorff, and second-countable or completely metrizable and continuum sized. Then X is Baire
![]() $\mathfrak c$
-resolvable.
$\mathfrak c$
-resolvable.
Proof Note that X is a Baire space. By Lemmas 4.12 and 4.13, the uncountable compact subsets of X form a
![]() $\mathfrak c$
-witnessing family for X. Therefore, by Theorem 4.11, X is Baire
$\mathfrak c$
-witnessing family for X. Therefore, by Theorem 4.11, X is Baire
![]() $\mathfrak c$
-resolvable.
$\mathfrak c$
-resolvable.
Remark 4.15. Lemma 4.12 can be generalized to the setting of Čech-complete spaces, under the assumption that no point has a least neighborhood (equivalently, that every point has infinite character: see, e.g., [Reference Engelking11, Exercise 3.12.11(b)]). This allows us to extend Theorem 4.14 to include any second-countable Čech-complete space with the latter property.
5 New completeness results for
 $\mathsf {S5}$
$\mathsf {S5}$
In this section we derive new completeness results for
![]() $\mathsf {S5}$
and its extensions using our new semantics of Baire algebras. We start by recalling that a map
$\mathsf {S5}$
and its extensions using our new semantics of Baire algebras. We start by recalling that a map
![]() $h \colon A\to B$
between two closure algebras
$h \colon A\to B$
between two closure algebras
![]() $(A,\mathbf {c}_A)$
and
$(A,\mathbf {c}_A)$
and
![]() $(B,\mathbf {c}_B)$
is a homomorphism of closure algebras if h is a homomorphism of Boolean algebras and
$(B,\mathbf {c}_B)$
is a homomorphism of closure algebras if h is a homomorphism of Boolean algebras and
![]() $h (\mathbf { c}_A a) = \mathbf {c}_B h(a)$
for each
$h (\mathbf { c}_A a) = \mathbf {c}_B h(a)$
for each
![]() $a\in A$
. We say that h is an embedding if it is injective, and that h is an isomorphism if it is bijective.
$a\in A$
. We say that h is an embedding if it is injective, and that h is an isomorphism if it is bijective.
Recall that if X and Y are topological spaces and
![]() $f\colon X\to Y$
, then f is continuous if
$f\colon X\to Y$
, then f is continuous if
![]() $f^{-1}(B)$
is open whenever
$f^{-1}(B)$
is open whenever
![]() $B\subseteq Y $
is open, open if
$B\subseteq Y $
is open, open if
![]() $f(A)$
is open whenever
$f(A)$
is open whenever
![]() $A\subseteq X$
is open, and an interior map if it is both continuous and open. It is well known (see, e.g., [Reference Rasiowa and Sikorski25, p. 99]) that if
$A\subseteq X$
is open, and an interior map if it is both continuous and open. It is well known (see, e.g., [Reference Rasiowa and Sikorski25, p. 99]) that if
![]() $f:X\to Y$
is an interior map, then
$f:X\to Y$
is an interior map, then
![]() $f^{-1}:\mathbf {Kur}(Y)\to \mathbf {Kur}(X)$
is a homomorphism of closure algebras. Moreover, if f is surjective, then
$f^{-1}:\mathbf {Kur}(Y)\to \mathbf {Kur}(X)$
is a homomorphism of closure algebras. Moreover, if f is surjective, then
![]() $f^{-1}$
is an embedding. To obtain analogous results for Baire algebras, it is sufficient to work with partial maps. We remind the reader that
$f^{-1}$
is an embedding. To obtain analogous results for Baire algebras, it is sufficient to work with partial maps. We remind the reader that
![]() $[A]$
denotes the equivalence class of A modulo the meager sets.
$[A]$
denotes the equivalence class of A modulo the meager sets.
Definition 5.1. Let
![]() $X,Y$
be arbitrary topological spaces and
$X,Y$
be arbitrary topological spaces and
![]() $f:X\to Y$
a partial map.
$f:X\to Y$
a partial map.
-
1. We say that f is defined almost everywhere if the complement of the domain of f is meager.
-
2. We call f non-degenerate if
 $B\subseteq Y$
meager implies that
$B\subseteq Y$
meager implies that
 $f^{-1}(B)$
is meager.
$f^{-1}(B)$
is meager. -
3. We define
 $h\colon \mathbf {Baire}(Y) \to \mathbf {Baire}(X)$
by
$h\colon \mathbf {Baire}(Y) \to \mathbf {Baire}(X)$
by  $$\begin{align*}h [ A ] = [f^{-1} (A)] \mbox{ for each } A\subseteq Y. \end{align*}$$
$$\begin{align*}h [ A ] = [f^{-1} (A)] \mbox{ for each } A\subseteq Y. \end{align*}$$
Lemma 5.2. Let
![]() $X ,Y$
be arbitrary topological spaces and
$X ,Y$
be arbitrary topological spaces and
![]() $f\colon X \to Y$
a partial map. If f is defined almost everywhere and is non-degenerate, then
$f\colon X \to Y$
a partial map. If f is defined almost everywhere and is non-degenerate, then
![]() $h\colon \mathbf {Baire}(Y) \to \mathbf {Baire}(X)$
is a well-defined homomorphism of Boolean algebras.
$h\colon \mathbf {Baire}(Y) \to \mathbf {Baire}(X)$
is a well-defined homomorphism of Boolean algebras.
Proof Let
![]() $A,{\kern-1pt}B {\kern-1pt}\subseteq{\kern-1pt} Y$
with
$A,{\kern-1pt}B {\kern-1pt}\subseteq{\kern-1pt} Y$
with
![]() $[A] {\kern-1pt}={\kern-1pt} [B]$
. Then
$[A] {\kern-1pt}={\kern-1pt} [B]$
. Then
![]() $A{\kern-1pt}\setminus{\kern-1pt} B$
is meager, so
$A{\kern-1pt}\setminus{\kern-1pt} B$
is meager, so
![]() $f^{-1}(A) \setminus f^{-1}(B) {\kern-1pt}= f^{-1} (A\setminus B)$
is meager since f is non-degenerate. By a symmetric argument,
$f^{-1}(A) \setminus f^{-1}(B) {\kern-1pt}= f^{-1} (A\setminus B)$
is meager since f is non-degenerate. By a symmetric argument,
![]() $f^{-1}(B) \setminus f^{-1}(A)$
is also meager. Thus,
$f^{-1}(B) \setminus f^{-1}(A)$
is also meager. Thus,
![]() $[f^{-1}(A)] = [f^{-1}(B)]$
, and hence h is well defined.
$[f^{-1}(A)] = [f^{-1}(B)]$
, and hence h is well defined.
In addition,
Therefore, h commutes with binary meets. To see that it also commutes with complements, let M be the complement of the domain of f. Then
![]() $X \setminus f^{-1}(A) = f^{-1}(Y \setminus A)\cup M$
. Since f is defined almost everywhere, M is meager, so
$X \setminus f^{-1}(A) = f^{-1}(Y \setminus A)\cup M$
. Since f is defined almost everywhere, M is meager, so
![]() $[ X \setminus f^{-1}(A) ] = [ f^{-1}(Y \setminus A) ]$
. Thus,
$[ X \setminus f^{-1}(A) ] = [ f^{-1}(Y \setminus A) ]$
. Thus,
Consequently, h is a well-defined homomorphism of Boolean algebras.
Note, however, that h may fail to be injective. To obtain an embedding of Boolean algebras, we need an additional condition on f.
Definition 5.3. We call a partial map
![]() $f\colon X\to Y$
exact if
$f\colon X\to Y$
exact if
![]() $f^{-1}(A)$
meager implies that A is meager for each
$f^{-1}(A)$
meager implies that A is meager for each
![]() $A\subseteq Y$
.
$A\subseteq Y$
.
Lemma 5.4. Let
![]() $X,Y$
be Baire spaces and let
$X,Y$
be Baire spaces and let
![]() $f\colon X\to Y$
be non-degenerate, exact, and defined almost everywhere. Then
$f\colon X\to Y$
be non-degenerate, exact, and defined almost everywhere. Then
![]() $h\colon \mathbf {Baire}(Y) \to \mathbf {Baire}(X)$
is an embedding of Boolean algebras.
$h\colon \mathbf {Baire}(Y) \to \mathbf {Baire}(X)$
is an embedding of Boolean algebras.
Proof By Lemma 5.2, h is a homomorphism of Boolean algebras. To see that it is an embedding, let
![]() $h [ A ] = h [ B ]$
. Then
$h [ A ] = h [ B ]$
. Then
![]() $ f^{-1}(A) \setminus f^{-1}(B) = f^{-1} (A\setminus B)$
is meager. Since f is exact,
$ f^{-1}(A) \setminus f^{-1}(B) = f^{-1} (A\setminus B)$
is meager. Since f is exact,
![]() $A \setminus B $
is meager. A symmetric argument yields that
$A \setminus B $
is meager. A symmetric argument yields that
![]() $B\setminus A $
is meager. Thus,
$B\setminus A $
is meager. Thus,
![]() $[A] = [B]$
, and hence h is an embedding.
$[A] = [B]$
, and hence h is an embedding.
Next we detail some conditions that will ensure that h is not only a Boolean homomorphism, but indeed a homomorphism of closure algebras.
Definition 5.5. Let
![]() $f\colon X \to Y$
be a partial map. We say that:
$f\colon X \to Y$
be a partial map. We say that:
-
1. f is Baire-continuous if V an open subset of Y implies that
 $[ f^{-1}(V) ]$
is an open element of
$[ f^{-1}(V) ]$
is an open element of
 $\mathbf {Baire}(X)$
;
$\mathbf {Baire}(X)$
; -
2. f is Baire-open if U a nonempty open subset and M a meager subset of X imply that
 $[f( U \setminus M )]$
is a nonzero open element of
$[f( U \setminus M )]$
is a nonzero open element of
 $\mathbf {Baire}(Y)$
;
$\mathbf {Baire}(Y)$
; -
3. f is a Baire map if it is defined almost everywhere and is non-degenerate, Baire-continuous, and Baire-open.
Remark 5.6. If a Baire map
![]() $f\colon X\to Y$
exists, then X must be a Baire space. This is because if
$f\colon X\to Y$
exists, then X must be a Baire space. This is because if
![]() $U\subseteq X$
were a nonempty open meager set, then
$U\subseteq X$
were a nonempty open meager set, then
![]() $ [ f(U\setminus U) ] = 0$
in
$ [ f(U\setminus U) ] = 0$
in
![]() $\mathbf {Baire}(Y)$
, so f could not be Baire-open.
$\mathbf {Baire}(Y)$
, so f could not be Baire-open.
Lemma 5.7. Let
![]() $X,Y$
be topological spaces. If
$X,Y$
be topological spaces. If
![]() $f\colon X\to Y$
is a Baire map, then
$f\colon X\to Y$
is a Baire map, then
![]() $h\colon \mathbf {Baire}(Y) \to \mathbf {Baire}(X)$
is a homomorphism of closure algebras. If in addition f is exact, then h is an embedding of closure algebras.
$h\colon \mathbf {Baire}(Y) \to \mathbf {Baire}(X)$
is a homomorphism of closure algebras. If in addition f is exact, then h is an embedding of closure algebras.
Proof By Lemma 5.2, h is a homomorphism of Boolean algebras. Let
![]() $A\subseteq Y$
. We first show that
$A\subseteq Y$
. We first show that
![]() $\mathbf {c} h [ A ] \sqsubseteq h \mathbf {c} [ A ] $
. Since
$\mathbf {c} h [ A ] \sqsubseteq h \mathbf {c} [ A ] $
. Since
![]() $\mathbf {c} [ A]$
is closed, there is a closed set
$\mathbf {c} [ A]$
is closed, there is a closed set
![]() $D\subseteq Y$
such that
$D\subseteq Y$
such that
![]() $[D] = \mathbf {c} [ A]$
. Because h is a homomorphism of Boolean algebras, it is order preserving. Therefore,
$[D] = \mathbf {c} [ A]$
. Because h is a homomorphism of Boolean algebras, it is order preserving. Therefore,
![]() $[A] \sqsubseteq \mathbf {c} [ A ]$
implies
$[A] \sqsubseteq \mathbf {c} [ A ]$
implies
![]() $h [ A ] \sqsubseteq h \mathbf {c}[ A ] = [f^{-1}( D )]$
. Let
$h [ A ] \sqsubseteq h \mathbf {c}[ A ] = [f^{-1}( D )]$
. Let
![]() $U=Y\setminus D$
and recall that M is the complement of the domain of f. Since U is open in Y and M is meager in X, we have
$U=Y\setminus D$
and recall that M is the complement of the domain of f. Since U is open in Y and M is meager in X, we have
Because f is Baire-continuous and U is open,
![]() $[f^{-1}(U)]$
is open, hence
$[f^{-1}(U)]$
is open, hence
![]() $[f^{-1}( D )]$
is closed in
$[f^{-1}( D )]$
is closed in
![]() $\mathbf {Baire}(X)$
. Thus,
$\mathbf {Baire}(X)$
. Thus,
![]() $\mathbf {c} h [ A ] \sqsubseteq [f^{-1}( D )] = h \mathbf {c} [A] $
by the definition of closure.
$\mathbf {c} h [ A ] \sqsubseteq [f^{-1}( D )] = h \mathbf {c} [A] $
by the definition of closure.
We next show that
![]() $h \mathbf {c} [A] \sqsubseteq \mathbf {c} h [ A ]$
. There is a closed set
$h \mathbf {c} [A] \sqsubseteq \mathbf {c} h [ A ]$
. There is a closed set
![]() $C \subseteq X$
such that
$C \subseteq X$
such that
![]() $\mathbf {c} h [A] = [C]$
. Let D be as above and, using the fact that f is Baire-continuous, write
$\mathbf {c} h [A] = [C]$
. Let D be as above and, using the fact that f is Baire-continuous, write
![]() $[f^{-1}(D)] = [F]$
, where
$[f^{-1}(D)] = [F]$
, where
![]() $F\subseteq X$
is closed. Let
$F\subseteq X$
is closed. Let
![]() $V = \mathbf {i} F \setminus C $
. Since
$V = \mathbf {i} F \setminus C $
. Since
![]() $ F $
is closed in X, we have
$ F $
is closed in X, we have
![]() $[ \mathbf {i} F ] = [F] = [ f^{-1} (D) ]$
. Therefore,
$[ \mathbf {i} F ] = [F] = [ f^{-1} (D) ]$
. Therefore,
so it suffices to show that
![]() $V=\varnothing $
. Suppose otherwise. Since
$V=\varnothing $
. Suppose otherwise. Since
![]() $[f^{-1}(A)] \sqsubseteq [C]$
, we have that
$[f^{-1}(A)] \sqsubseteq [C]$
, we have that
![]() $f^{-1}(A)\setminus C$
is meager, so
$f^{-1}(A)\setminus C$
is meager, so
![]() $L:= f^ {-1} (A) \cap V$
is meager. Because f is Baire-open, L is meager, and V is nonempty open,
$L:= f^ {-1} (A) \cap V$
is meager. Because f is Baire-open, L is meager, and V is nonempty open,
![]() $[f(V) \setminus A] = [f( V\setminus f^{-1} (A))] =[f( V\setminus L)]$
is nonzero and open in
$[f(V) \setminus A] = [f( V\setminus f^{-1} (A))] =[f( V\setminus L)]$
is nonzero and open in
![]() $\mathbf {Baire}(Y)$
. Thus,
$\mathbf {Baire}(Y)$
. Thus,
![]() $\mathbf {c} [A] - [f(V) \setminus A] \sqsubset \mathbf {c} [A]$
. Recall that we chose D so that
$\mathbf {c} [A] - [f(V) \setminus A] \sqsubset \mathbf {c} [A]$
. Recall that we chose D so that
![]() $\mathbf {c} [A] = [D]$
. In particular,
$\mathbf {c} [A] = [D]$
. In particular,
![]() $[A] \sqsubseteq [D]$
. Since
$[A] \sqsubseteq [D]$
. Since
![]() $A \setminus (D \setminus (f(V) \setminus A)) = A\setminus D$
and the latter is meager, we see that
$A \setminus (D \setminus (f(V) \setminus A)) = A\setminus D$
and the latter is meager, we see that
As
![]() $\mathbf {c} [A] - [f(V) \setminus A]$
is closed in
$\mathbf {c} [A] - [f(V) \setminus A]$
is closed in
![]() $\mathbf {Baire}(Y)$
, this contradicts the definition of
$\mathbf {Baire}(Y)$
, this contradicts the definition of
![]() $\mathbf {c}[A]$
. Consequently,
$\mathbf {c}[A]$
. Consequently,
![]() $V = \varnothing $
, as required.
$V = \varnothing $
, as required.
Finally, if f is exact, then it follows from Lemma 5.4 that h is an embedding.
If Y is an
![]() $\mathsf {S5}$
-frame, it follows from Example 3.2(1) that
$\mathsf {S5}$
-frame, it follows from Example 3.2(1) that
![]() $\mathbf {Kur}(Y)$
is isomorphic to
$\mathbf {Kur}(Y)$
is isomorphic to
![]() $\mathbf {Baire}(Y)$
, so we may regard h as a map from
$\mathbf {Baire}(Y)$
, so we may regard h as a map from
![]() $\mathbf {Kur}(Y)$
to
$\mathbf {Kur}(Y)$
to
![]() $\mathbf {Baire}(X)$
. Since the only meager subset of an
$\mathbf {Baire}(X)$
. Since the only meager subset of an
![]() $\mathsf {S5}$
-frame is
$\mathsf {S5}$
-frame is
![]() $\varnothing $
, the next lemma is immediate.
$\varnothing $
, the next lemma is immediate.
Lemma 5.8. Let X be a Baire space, Y an
![]() $\mathsf {S5}$
-frame, and
$\mathsf {S5}$
-frame, and
![]() $f\colon X\to Y$
a Baire map. Then f is exact iff
$f\colon X\to Y$
a Baire map. Then f is exact iff
![]() $f^{-1}( y )$
is non-meager for each
$f^{-1}( y )$
is non-meager for each
![]() $y\in Y$
.
$y\in Y$
.
Recall that for a nonzero cardinal
![]() $\kappa $
,
$\kappa $
,
![]() $\mathfrak C_\kappa $
denotes the
$\mathfrak C_\kappa $
denotes the
![]() $\kappa $
-cluster. By [Reference Bezhanishvili, Bezhanishvili, Lucero-Bryan and van Mill2, Lemma 5.9], a space X is
$\kappa $
-cluster. By [Reference Bezhanishvili, Bezhanishvili, Lucero-Bryan and van Mill2, Lemma 5.9], a space X is
![]() $\kappa $
-resolvable iff there is an interior map from X onto
$\kappa $
-resolvable iff there is an interior map from X onto
![]() $\mathfrak C_\kappa $
. We have the following analogue of this result for Baire algebras.
$\mathfrak C_\kappa $
. We have the following analogue of this result for Baire algebras.
Lemma 5.9. Let X be a Baire space and
![]() $\kappa $
a nonzero cardinal. Then X is Baire
$\kappa $
a nonzero cardinal. Then X is Baire
![]() $\kappa $
-resolvable iff there is an exact Baire map
$\kappa $
-resolvable iff there is an exact Baire map
![]() $f\colon X \to \mathfrak C_\kappa $
.
$f\colon X \to \mathfrak C_\kappa $
.
Proof Let
![]() $(w_\iota )_{\iota <\kappa }$
be an enumeration of
$(w_\iota )_{\iota <\kappa }$
be an enumeration of
![]() $\mathfrak C_\kappa $
. First suppose that X is Baire
$\mathfrak C_\kappa $
. First suppose that X is Baire
![]() $\kappa $
-resolvable, and let
$\kappa $
-resolvable, and let
![]() $(A_\iota )_{\iota <\kappa }$
be a Baire
$(A_\iota )_{\iota <\kappa }$
be a Baire
![]() $\kappa $
-resolution of X. Define
$\kappa $
-resolution of X. Define
![]() $f\colon X\to \mathfrak C_\kappa $
by setting
$f\colon X\to \mathfrak C_\kappa $
by setting
![]() $f(x) = w_\iota $
provided
$f(x) = w_\iota $
provided
![]() $x\in A_\iota $
. Then f is a total onto map. Since f is total, it is defined almost everywhere, and f is non-degenerate because
$x\in A_\iota $
. Then f is a total onto map. Since f is total, it is defined almost everywhere, and f is non-degenerate because
![]() $\varnothing $
is the only meager subset of
$\varnothing $
is the only meager subset of
![]() $\mathfrak C_\kappa $
. Since
$\mathfrak C_\kappa $
. Since
![]() $\varnothing ,\mathfrak C_\kappa $
are the only opens of
$\varnothing ,\mathfrak C_\kappa $
are the only opens of
![]() $\mathfrak C_\kappa $
, it is clear that f is continuous, hence Baire-continuous. To see that f is Baire-open, let
$\mathfrak C_\kappa $
, it is clear that f is continuous, hence Baire-continuous. To see that f is Baire-open, let
![]() $U\subseteq X$
be nonempty open and
$U\subseteq X$
be nonempty open and
![]() $M\subseteq X$
meager. Since each
$M\subseteq X$
meager. Since each
![]() $A_\iota $
is Baire-dense,
$A_\iota $
is Baire-dense,
![]() $A_\iota \cap (U\setminus M)$
is non-meager, hence nonempty, so
$A_\iota \cap (U\setminus M)$
is non-meager, hence nonempty, so
![]() $w_\iota \in f(U \setminus M)$
, and hence
$w_\iota \in f(U \setminus M)$
, and hence
![]() $f(U \setminus M) = \mathfrak C_\kappa $
. Therefore, f is a Baire map. Finally,
$f(U \setminus M) = \mathfrak C_\kappa $
. Therefore, f is a Baire map. Finally,
![]() $f^{-1}(w_\iota ) = A_\iota $
, which is non-meager. Thus, f is exact by Lemma 5.8.
$f^{-1}(w_\iota ) = A_\iota $
, which is non-meager. Thus, f is exact by Lemma 5.8.
Next suppose that
![]() $f\colon X\to \mathfrak C_\kappa $
is an exact Baire map. By Lemma 5.8, each
$f\colon X\to \mathfrak C_\kappa $
is an exact Baire map. By Lemma 5.8, each
![]() $f^{-1}(w_\iota )$
is non-meager, and we can enlarge
$f^{-1}(w_\iota )$
is non-meager, and we can enlarge
![]() $f^{-1}(w_0)$
to obtain a partition of X if needed. By identifying
$f^{-1}(w_0)$
to obtain a partition of X if needed. By identifying
![]() $\mathbf {Baire}(\mathfrak C_\kappa )$
with
$\mathbf {Baire}(\mathfrak C_\kappa )$
with
![]() $\mathbf {Kur}(\mathfrak C_\kappa )$
and applying Lemma 5.7,
$\mathbf {Kur}(\mathfrak C_\kappa )$
and applying Lemma 5.7,
![]() $h:\mathbf {Kur}(\mathfrak C_\kappa ) \to \mathbf {Baire}(X)$
is a homomorphism of closure algebras. Therefore, for each
$h:\mathbf {Kur}(\mathfrak C_\kappa ) \to \mathbf {Baire}(X)$
is a homomorphism of closure algebras. Therefore, for each
![]() $\iota <\kappa $
,
$\iota <\kappa $
,
Thus,
![]() $( f^{-1}(w_\iota ) )_{\iota <\kappa }$
witnesses that X is Baire
$( f^{-1}(w_\iota ) )_{\iota <\kappa }$
witnesses that X is Baire
![]() $\kappa $
-resolvable.
$\kappa $
-resolvable.
We are ready to prove our first completeness result. For this we recall that
![]() $\mathsf {S5}^\lambda $
denotes the variant of
$\mathsf {S5}^\lambda $
denotes the variant of
![]() $\mathsf {S5}$
with
$\mathsf {S5}$
with
![]() $\lambda $
-many variables, and if
$\lambda $
-many variables, and if
![]() $\lambda <\omega $
, then
$\lambda <\omega $
, then
![]() $\mathsf {S5}_\lambda $
is the extension of
$\mathsf {S5}_\lambda $
is the extension of
![]() $\mathsf {S5}$
axiomatized by
$\mathsf {S5}$
axiomatized by
![]() $\mathrm { Alt}_{\lambda }$
.
$\mathrm { Alt}_{\lambda }$
.
Theorem 5.10. Let X be a Baire space,
![]() $\lambda $
a nonzero cardinal, and suppose that X is Baire
$\lambda $
a nonzero cardinal, and suppose that X is Baire
![]() $\lambda $
-resolvable.
$\lambda $
-resolvable.
-
(1) If
 $\lambda \geq \omega $
, then
$\lambda \geq \omega $
, then
 $\mathsf {S5}^\lambda $
is sound and strongly complete for
$\mathsf {S5}^\lambda $
is sound and strongly complete for
 $\mathbf {Baire}(X)$
.
$\mathbf {Baire}(X)$
. -
(2) If
 $\lambda < \omega $
and X is nowhere Baire
$\lambda < \omega $
and X is nowhere Baire
 $(\lambda +1)$
-resolvable, then
$(\lambda +1)$
-resolvable, then
 $ \mathsf {S5}_\lambda $
is sound and strongly complete for
$ \mathsf {S5}_\lambda $
is sound and strongly complete for
 $\mathbf {Baire}(X)$
.
$\mathbf {Baire}(X)$
.
Proof (1) Soundness follows from the fact that
![]() $\mathbf {Baire}(X)$
is a monadic algebra (see Theorem 3.8). For completeness, let
$\mathbf {Baire}(X)$
is a monadic algebra (see Theorem 3.8). For completeness, let
![]() $\Gamma \models _{\mathbf {Baire}(X)} \varphi $
. By Lemma 5.9, there is an exact Baire map
$\Gamma \models _{\mathbf {Baire}(X)} \varphi $
. By Lemma 5.9, there is an exact Baire map
![]() $f\colon X\to \mathfrak C_\lambda $
. Since
$f\colon X\to \mathfrak C_\lambda $
. Since
![]() $\mathbf {Kur}( \mathfrak C_\lambda )$
is isomorphic to
$\mathbf {Kur}( \mathfrak C_\lambda )$
is isomorphic to
![]() $\mathbf { Baire}( \mathfrak C_\lambda )$
, by Lemma 5.7
$\mathbf { Baire}( \mathfrak C_\lambda )$
, by Lemma 5.7
![]() $\mathbf {Kur}( \mathfrak C_\lambda )$
embeds into
$\mathbf {Kur}( \mathfrak C_\lambda )$
embeds into
![]() $\mathbf {Baire}(X)$
. Therefore,
$\mathbf {Baire}(X)$
. Therefore,
![]() $\Gamma \models _{ \mathfrak C_\lambda } \varphi $
. Thus,
$\Gamma \models _{ \mathfrak C_\lambda } \varphi $
. Thus,
![]() $\Gamma \vdash _{\mathsf {S5}^\lambda } \varphi $
by Theorem 2.11.
$\Gamma \vdash _{\mathsf {S5}^\lambda } \varphi $
by Theorem 2.11.
(2) We first prove completeness. Suppose
![]() $\Gamma \models _{\mathbf {Baire}(X)} \varphi $
. By Lemma 5.9, there is an exact Baire map
$\Gamma \models _{\mathbf {Baire}(X)} \varphi $
. By Lemma 5.9, there is an exact Baire map
![]() $f\colon X\to \mathfrak C_\lambda $
. By Lemma 5.7,
$f\colon X\to \mathfrak C_\lambda $
. By Lemma 5.7,
![]() $\mathbf {Kur}( \mathfrak C_\lambda )$
embeds into
$\mathbf {Kur}( \mathfrak C_\lambda )$
embeds into
![]() $\mathbf {Baire}(X)$
. Therefore,
$\mathbf {Baire}(X)$
. Therefore,
![]() $\Gamma \models _{ \mathfrak C_\lambda } \varphi $
. Thus,
$\Gamma \models _{ \mathfrak C_\lambda } \varphi $
. Thus,
![]() $\Gamma \vdash _{\mathsf {S5}_\lambda } \varphi $
by Theorem 2.11.
$\Gamma \vdash _{\mathsf {S5}_\lambda } \varphi $
by Theorem 2.11.
To prove soundness, suppose that
![]() $\mathsf {S5}_\lambda $
is not sound for X, and fix a valuation
$\mathsf {S5}_\lambda $
is not sound for X, and fix a valuation ![]() falsifying the
falsifying the
![]() $\mathsf {S5}_\lambda $
axiom
$\mathsf {S5}_\lambda $
axiom
![]() $\mathrm {Alt}_{\lambda }$
. Since this axiom is a Boolean combination of formulas
$\mathrm {Alt}_{\lambda }$
. Since this axiom is a Boolean combination of formulas
![]() $\Diamond \psi $
, we have that
$\Diamond \psi $
, we have that ![]() is clopen, so we can choose nonempty open U with
is clopen, so we can choose nonempty open U with ![]() . Then
. Then
 $$ \begin{align} [U] \sqsubseteq \bigg[\!\!\bigg[ {\bigwedge_{i = 1}^{\lambda + 1} \Diamond p_i} \bigg]\!\!\bigg] \end{align} $$
$$ \begin{align} [U] \sqsubseteq \bigg[\!\!\bigg[ {\bigwedge_{i = 1}^{\lambda + 1} \Diamond p_i} \bigg]\!\!\bigg] \end{align} $$
and
 $$ \begin{align} [U] \sqcap \bigg[\!\!\bigg[ { \bigvee_{1\leq i<j\leq \lambda + 1} \Diamond(p_i\wedge p_j) } \bigg]\!\!\bigg] = 0. \end{align} $$
$$ \begin{align} [U] \sqcap \bigg[\!\!\bigg[ { \bigvee_{1\leq i<j\leq \lambda + 1} \Diamond(p_i\wedge p_j) } \bigg]\!\!\bigg] = 0. \end{align} $$
For
![]() $i\leq \lambda+1 $
, let
$i\leq \lambda+1 $
, let
![]() $P^{\prime }_i$
be such that
$P^{\prime }_i$
be such that ![]() . From (*) we obtain for each
. From (*) we obtain for each
![]() $i\le \lambda+1 $
that
$i\le \lambda+1 $
that
![]() $[U] \sqsubseteq \mathbf {c} [P^{\prime }_i ]$
, which means that
$[U] \sqsubseteq \mathbf {c} [P^{\prime }_i ]$
, which means that
![]() $P^{\prime }_i$
is nowhere meager in U, i.e., if
$P^{\prime }_i$
is nowhere meager in U, i.e., if
![]() ${U'\subseteq U}$
is nonempty open then
${U'\subseteq U}$
is nonempty open then
![]() $P^{\prime }_i\cap U'$
is non-meager. From (†) it follows that
$P^{\prime }_i\cap U'$
is non-meager. From (†) it follows that ![]() whenever
whenever
![]() $i<j\leq \lambda +1$
, so
$i<j\leq \lambda +1$
, so
![]() $U\cap P^{\prime }_i \cap P^{\prime }_j$
is meager. Since
$U\cap P^{\prime }_i \cap P^{\prime }_j$
is meager. Since
![]() $\lambda $
is finite, we can then replace each
$\lambda $
is finite, we can then replace each
![]() $P^{\prime }_i$
by some
$P^{\prime }_i$
by some
![]() $P_i$
in such a way that
$P_i$
in such a way that
![]() $[P_i] = [P^{\prime }_i]$
and
$[P_i] = [P^{\prime }_i]$
and
![]() $\{P_i \mid i \leq \lambda+1 \}$
forms a partition of U, witnessing that U is Baire
$\{P_i \mid i \leq \lambda+1 \}$
forms a partition of U, witnessing that U is Baire
![]() $(\lambda + 1)$
-resolvable, hence X is somewhere Baire
$(\lambda + 1)$
-resolvable, hence X is somewhere Baire
![]() $(\lambda + 1)$
-resolvable, contrary to our assumption.
$(\lambda + 1)$
-resolvable, contrary to our assumption.
As a consequence of Theorems 5.10(1) and 4.14, we arrive at the following analogue of the McKinsey–Tarski theorem:
Corollary 5.11. Let X be a crowded space which is either completely metrizable and of cardinality continuum, or second-countable locally compact Hausdorff. Then
![]() $\mathsf {S5}^{\mathfrak c}$
is sound and strongly complete for
$\mathsf {S5}^{\mathfrak c}$
is sound and strongly complete for
![]() $\mathbf { Baire}(X)$
.
$\mathbf { Baire}(X)$
.
In particular, we obtain:
Corollary 5.12.
![]() $\mathsf {S5}$
is the logic of
$\mathsf {S5}$
is the logic of
![]() $\mathbf {Baire}(X)$
whenever X is:
$\mathbf {Baire}(X)$
whenever X is:
-
(1)
 $\mathbb R^n$
for any
$\mathbb R^n$
for any
 $n \geq 1$
.
$n \geq 1$
. -
(2) Any perfect closed subset of
 $\mathbb R^n$
, including the Cantor space and the interval
$\mathbb R^n$
, including the Cantor space and the interval
 $[0,1]$
.
$[0,1]$
. -
(3) The Banach space
 $\ell ^p$
for
$\ell ^p$
for
 $p\in [1,\infty ]$
.
$p\in [1,\infty ]$
.
Recall that
![]() $\ell ^p$
is the normed vector space whose elements are functions
$\ell ^p$
is the normed vector space whose elements are functions
![]() $f\colon \mathbb N\to \mathbb R$
whose p-norm converges (see [Reference Cohn8] for details). Note that we may allow
$f\colon \mathbb N\to \mathbb R$
whose p-norm converges (see [Reference Cohn8] for details). Note that we may allow
![]() $p=\infty $
since
$p=\infty $
since
![]() $|\ell ^\infty | = \mathfrak c$
, despite not being second-countable.
$|\ell ^\infty | = \mathfrak c$
, despite not being second-countable.
Remark 5.13. On the other hand, since
![]() $\mathbb Q$
is meager,
$\mathbb Q$
is meager,
![]() $\mathbf {Baire}(\mathbb Q)$
is the trivial algebra, and hence its logic is the contradictory logic, i.e., the logic axiomatized by
$\mathbf {Baire}(\mathbb Q)$
is the trivial algebra, and hence its logic is the contradictory logic, i.e., the logic axiomatized by
![]() $\bot $
. This is in contrast with the McKinsey–Tarski theorem that the logic of
$\bot $
. This is in contrast with the McKinsey–Tarski theorem that the logic of
![]() $\mathbf {Kur}(\mathbb Q)$
is
$\mathbf {Kur}(\mathbb Q)$
is
![]() $\mathsf {S4}$
.
$\mathsf {S4}$
.
By Theorem 5.10(2), if X is a Baire space that is Baire n-resolvable and nowhere Baire
![]() $(n+1)$
-resolvable, then the logic of
$(n+1)$
-resolvable, then the logic of
![]() $\mathbf {Baire}(X)$
is
$\mathbf {Baire}(X)$
is
![]() $\mathsf {S5}_n$
. As we next show, we can avoid verifying whether X is nowhere Baire
$\mathsf {S5}_n$
. As we next show, we can avoid verifying whether X is nowhere Baire
![]() $(n+1)$
-resolvable by constructing a subalgebra of
$(n+1)$
-resolvable by constructing a subalgebra of
![]() $\mathbf {Baire}(X)$
whose logic is
$\mathbf {Baire}(X)$
whose logic is
![]() $\mathsf {S5}_n$
. For this we require the following decomposition lemma, which follows from similar decompositions in the theory of
$\mathsf {S5}_n$
. For this we require the following decomposition lemma, which follows from similar decompositions in the theory of
![]() $\ell $
-groups; see, e.g., [Reference Bezhanishvili, Morandi, Olberding, Nguyen and Kreinovich5] and the references therein. To keep the paper self-contained, we give a proof.
$\ell $
-groups; see, e.g., [Reference Bezhanishvili, Morandi, Olberding, Nguyen and Kreinovich5] and the references therein. To keep the paper self-contained, we give a proof.
Lemma 5.14. Let A be a monadic algebra,
![]() $A_0$
its subalgebra of all clopen elements, B a Boolean subalgebra of A, and C the Boolean subalgebra of A generated by
$A_0$
its subalgebra of all clopen elements, B a Boolean subalgebra of A, and C the Boolean subalgebra of A generated by
![]() $A_0\cup B$
.
$A_0\cup B$
.
-
(1) C is a monadic subalgebra of A.
-
(2) Each
 $c\in C$
can be written as
$c\in C$
can be written as
 $c=\bigvee _{i=1}^n(a_i\wedge b_i)$
, where
$c=\bigvee _{i=1}^n(a_i\wedge b_i)$
, where
 $a_1,\dots ,a_n\in A_0$
are pairwise orthogonal and
$a_1,\dots ,a_n\in A_0$
are pairwise orthogonal and
 $b_1,\dots ,b_n\in B$
.
$b_1,\dots ,b_n\in B$
. -
(3) Each
 $c^1,\ldots ,c^n\in C$
can be written in the compatible form
$c^1,\ldots ,c^n\in C$
can be written in the compatible form
 $c^j=\bigvee _{i=1}^n(a_i\wedge b^j_i)$
where
$c^j=\bigvee _{i=1}^n(a_i\wedge b^j_i)$
where
 $a_1,\dots ,a_n\in A_0$
are pairwise orthogonal and each
$a_1,\dots ,a_n\in A_0$
are pairwise orthogonal and each
 $b^j_i\in B$
.
$b^j_i\in B$
.
Proof (1) For
![]() $a\in C$
we have
$a\in C$
we have
![]() $\mathbf {c} a\in A_0 \subseteq C$
(since closed elements are clopen by Theorem 3.4). Thus, C is a monadic subalgebra of A.
$\mathbf {c} a\in A_0 \subseteq C$
(since closed elements are clopen by Theorem 3.4). Thus, C is a monadic subalgebra of A.
(2) Since C is a Boolean subalgebra of A, it is well known (see, e.g., [Reference Rasiowa and Sikorski25, p. 74]) that each
![]() $c\in C$
can be written as
$c\in C$
can be written as
![]() $c=\bigvee _{i=1}^n\bigwedge _{j=1}^{m_j}d_{ij}$
where either
$c=\bigvee _{i=1}^n\bigwedge _{j=1}^{m_j}d_{ij}$
where either
![]() $d_{ij}\in A_0\cup B$
or
$d_{ij}\in A_0\cup B$
or
![]() $-d_{ij}\in A_0\cup B$
. Since both
$-d_{ij}\in A_0\cup B$
. Since both
![]() $A_0$
and B are Boolean subalgebras, we may assume that
$A_0$
and B are Boolean subalgebras, we may assume that
![]() $d_{ij}\in A_0\cup B$
; and gathering together the elements in
$d_{ij}\in A_0\cup B$
; and gathering together the elements in
![]() $A_0$
and B, we may write
$A_0$
and B, we may write
![]() $\bigwedge _{j=1}^{m_j}d_{ij}=a_i\wedge b_i$
where
$\bigwedge _{j=1}^{m_j}d_{ij}=a_i\wedge b_i$
where
![]() $a_i\in A_0$
and
$a_i\in A_0$
and
![]() $b_i\in B$
. Therefore, each
$b_i\in B$
. Therefore, each
![]() $c\in C$
can be written as
$c\in C$
can be written as
![]() $c=\bigvee _{i=1}^n(a_i\wedge b_i)$
where
$c=\bigvee _{i=1}^n(a_i\wedge b_i)$
where
![]() $a_i\in A_0$
and
$a_i\in A_0$
and
![]() $b_i\in B$
. It is left to prove that the
$b_i\in B$
. It is left to prove that the
![]() $a_i$
can be chosen pairwise orthogonal. But this is a standard argument. Indeed, if
$a_i$
can be chosen pairwise orthogonal. But this is a standard argument. Indeed, if
![]() $c=(a_1\wedge b_1)\vee (a_2\wedge b_2)$
, then we may write
$c=(a_1\wedge b_1)\vee (a_2\wedge b_2)$
, then we may write
 $$ \begin{align*} c &= (a_1\wedge b_1)\vee(a_2\wedge b_2) \\ &= \left[\left( (a_1 - a_2) \wedge b_1\right) \vee \left((a_1\wedge a_2)\wedge b_1\right)\right] \vee \left[\left((a_2 \wedge a_1) \wedge b_2\right) \vee \left((a_2 - a_1) \wedge b_2\right)\right] \\ &= \left( (a_1 - a_2) \wedge b_1\right) \vee \left((a_1\wedge a_2)\wedge(b_1\vee b_2)\right) \vee \left((a_2 - a_1) \wedge b_2\right), \end{align*} $$
$$ \begin{align*} c &= (a_1\wedge b_1)\vee(a_2\wedge b_2) \\ &= \left[\left( (a_1 - a_2) \wedge b_1\right) \vee \left((a_1\wedge a_2)\wedge b_1\right)\right] \vee \left[\left((a_2 \wedge a_1) \wedge b_2\right) \vee \left((a_2 - a_1) \wedge b_2\right)\right] \\ &= \left( (a_1 - a_2) \wedge b_1\right) \vee \left((a_1\wedge a_2)\wedge(b_1\vee b_2)\right) \vee \left((a_2 - a_1) \wedge b_2\right), \end{align*} $$
where
![]() $a_1 - a_2, a_1\wedge a_2, a_2 - a_1\in A_0$
are pairwise orthogonal and
$a_1 - a_2, a_1\wedge a_2, a_2 - a_1\in A_0$
are pairwise orthogonal and
![]() $b_1, b_1\vee b_2, b_2\in B$
. Now a simple inductive argument finishes the proof.
$b_1, b_1\vee b_2, b_2\in B$
. Now a simple inductive argument finishes the proof.
(3) We only consider the case of two elements
![]() $c,d$
as the general case follows by simple induction. By (2), we may write
$c,d$
as the general case follows by simple induction. By (2), we may write
![]() $c=\bigvee _{i=1}^n(a_i\wedge b_i)$
where
$c=\bigvee _{i=1}^n(a_i\wedge b_i)$
where
![]() $a_1,\dots ,a_n\in A_0$
are pairwise orthogonal and
$a_1,\dots ,a_n\in A_0$
are pairwise orthogonal and
![]() $b_1,\dots ,b_n\in B$
. Similarly
$b_1,\dots ,b_n\in B$
. Similarly
![]() $d=\bigvee _{j=1}^m(e_j\wedge f_j)$
where
$d=\bigvee _{j=1}^m(e_j\wedge f_j)$
where
![]() $e_1,\dots ,e_m\in A_0$
are pairwise orthogonal and
$e_1,\dots ,e_m\in A_0$
are pairwise orthogonal and
![]() $f_1,\dots ,f_m\in B$
. By letting
$f_1,\dots ,f_m\in B$
. By letting
![]() $a_{n+1}=\lnot \bigvee _{i=1}^n a_i$
and
$a_{n+1}=\lnot \bigvee _{i=1}^n a_i$
and
![]() $b_{n+1}=0$
we may assume that
$b_{n+1}=0$
we may assume that
![]() $\bigvee _{i=1}^n a_i=1$
, and similarly
$\bigvee _{i=1}^n a_i=1$
, and similarly
![]() $\bigvee _{j=1}^m e_j=1$
. But then
$\bigvee _{j=1}^m e_j=1$
. But then
 $$\begin{align*}c=\bigvee_{i=1}^n\bigvee_{j=1}^m((a_i\wedge e_j)\wedge b_i) \mbox{ and } d=\bigvee_{j=1}^m\bigvee_{i=1}^n((a_i\wedge e_j)\wedge f_j). \end{align*}$$
$$\begin{align*}c=\bigvee_{i=1}^n\bigvee_{j=1}^m((a_i\wedge e_j)\wedge b_i) \mbox{ and } d=\bigvee_{j=1}^m\bigvee_{i=1}^n((a_i\wedge e_j)\wedge f_j). \end{align*}$$
Clearly
are pairwise orthogonal and are in
![]() $A_0$
; also each of
$A_0$
; also each of
![]() $b_i,f_j$
is in B (and may appear multiple times in the decomposition).
$b_i,f_j$
is in B (and may appear multiple times in the decomposition).
Theorem 5.15. Let X be a Baire space and
![]() $n<\omega $
. If X is Baire n-resolvable, then
$n<\omega $
. If X is Baire n-resolvable, then
![]() $\mathbf {Baire}(X)$
has a subalgebra A containing all clopens of
$\mathbf {Baire}(X)$
has a subalgebra A containing all clopens of
![]() $\mathbf {Baire}(X)$
such that
$\mathbf {Baire}(X)$
such that
![]() $ \mathsf {S5}_n$
is sound and strongly complete for A.
$ \mathsf {S5}_n$
is sound and strongly complete for A.
Proof Let
![]() $\mathfrak C_n=\{w_1,\ldots ,w_n\}$
be the n-cluster. By Lemmas 5.7 and 5.9, there is an embedding
$\mathfrak C_n=\{w_1,\ldots ,w_n\}$
be the n-cluster. By Lemmas 5.7 and 5.9, there is an embedding
![]() $h\colon{\kern-1pt} \mathbf {Kur}(\mathfrak C_n){\kern-1pt}\to{\kern-1pt} \mathbf {Baire}(X)$
. Let
$h\colon{\kern-1pt} \mathbf {Kur}(\mathfrak C_n){\kern-1pt}\to{\kern-1pt} \mathbf {Baire}(X)$
. Let
![]() $A = h[\mathbf {Kur}(\mathfrak C_n)]$
and
$A = h[\mathbf {Kur}(\mathfrak C_n)]$
and
![]() $H{\kern-1pt} ={\kern-1pt} \{h(w) {\kern-1pt}\mid{\kern-1pt} w{\kern-1pt}\in{\kern-1pt} \mathfrak C_n\}$
. Then A is a monadic subalgebra of
$H{\kern-1pt} ={\kern-1pt} \{h(w) {\kern-1pt}\mid{\kern-1pt} w{\kern-1pt}\in{\kern-1pt} \mathfrak C_n\}$
. Then A is a monadic subalgebra of
![]() $\mathbf {Baire}(X)$
generated by H, and each
$\mathbf {Baire}(X)$
generated by H, and each
![]() $h(w)$
is an atom of A. Let B be the Boolean subalgebra of
$h(w)$
is an atom of A. Let B be the Boolean subalgebra of
![]() $\mathbf {Baire}(X)$
generated by A and the clopen elements of
$\mathbf {Baire}(X)$
generated by A and the clopen elements of
![]() $\mathbf {Baire}(X)$
. By Lemma 5.14(1), B is a monadic subalgebra of
$\mathbf {Baire}(X)$
. By Lemma 5.14(1), B is a monadic subalgebra of
![]() $\mathbf {Baire}(X)$
. We claim that the logic of B is
$\mathbf {Baire}(X)$
. We claim that the logic of B is
![]() $\mathsf {S5}_n$
.
$\mathsf {S5}_n$
.
Since
![]() $\mathsf {S5}_n$
is complete for
$\mathsf {S5}_n$
is complete for
![]() $\mathfrak C_n$
, it follows that
$\mathfrak C_n$
, it follows that
![]() $\mathsf {S5}_n$
is complete for B. It remains to check that
$\mathsf {S5}_n$
is complete for B. It remains to check that
![]() $\mathsf {S5}_n$
is also sound for B. For this it is sufficient to show that
$\mathsf {S5}_n$
is also sound for B. For this it is sufficient to show that
![]() $\mathrm {Alt}_{n}$
is valid in B. Let
$\mathrm {Alt}_{n}$
is valid in B. Let ![]() be a valuation on B. By Lemma 5.14(3), we may write each
be a valuation on B. By Lemma 5.14(3), we may write each ![]() in the form
in the form
![]() $\bigsqcup _{ \ell = 1}^m (u_\ell \sqcap a^i_\ell )$
, where the
$\bigsqcup _{ \ell = 1}^m (u_\ell \sqcap a^i_\ell )$
, where the
![]() $u_\ell $
are orthogonal clopens and the
$u_\ell $
are orthogonal clopens and the
![]() $a^i_\ell $
are elements of A. Therefore, since each
$a^i_\ell $
are elements of A. Therefore, since each
![]() $u_\ell $
is clopen,
$u_\ell $
is clopen,
![]() $\mathbf {c}(u_\ell \sqcap a_\ell ^i) = u_\ell \sqcap \mathbf {c} a_\ell ^i$
, so we have
$\mathbf {c}(u_\ell \sqcap a_\ell ^i) = u_\ell \sqcap \mathbf {c} a_\ell ^i$
, so we have

where the last equality uses distributivity plus the orthogonality of the
![]() $u_\ell $
, so that all cross-terms cancel. Similarly,
$u_\ell $
, so that all cross-terms cancel. Similarly,

So to show that ![]() , it suffices to show that
, it suffices to show that

Given that the
![]() $u_\ell $
are orthogonal, (3) holds iff, for each
$u_\ell $
are orthogonal, (3) holds iff, for each
![]() $\ell $
,
$\ell $
,

and for this it suffices to show that

So fix
![]() $\ell $
. Note that (4) holds trivially if
$\ell $
. Note that (4) holds trivially if
![]() $a^i_\ell = 0$
for some i (as the left-hand side is then zero), so we assume otherwise. Since A is generated by H, for each i there is
$a^i_\ell = 0$
for some i (as the left-hand side is then zero), so we assume otherwise. Since A is generated by H, for each i there is
![]() $w \in \mathfrak C_n$
such that
$w \in \mathfrak C_n$
such that
![]() $h(w ) \sqsubseteq a^i_\ell $
. Because
$h(w ) \sqsubseteq a^i_\ell $
. Because
![]() $| \mathfrak C_n | = n$
, the pigeonhole principle yields that there are
$| \mathfrak C_n | = n$
, the pigeonhole principle yields that there are
![]() $i\neq j$
and w so that
$i\neq j$
and w so that
![]() $h(w) \sqsubseteq a^i_\ell \sqcap a^j_\ell $
. But
$h(w) \sqsubseteq a^i_\ell \sqcap a^j_\ell $
. But
![]() $\mathbf {c} h(w) = 1$
, so
$\mathbf {c} h(w) = 1$
, so
![]() $\mathbf {c} (a^i_\ell \sqcap a^j_\ell ) = 1$
. Therefore,
$\mathbf {c} (a^i_\ell \sqcap a^j_\ell ) = 1$
. Therefore,

Thus, (4) holds and, since
![]() $\ell $
was arbitrary, we conclude that (3) holds, as needed.
$\ell $
was arbitrary, we conclude that (3) holds, as needed.
As a consequence of Theorems 5.15 and 4.14 we obtain:
Corollary 5.16. Let X be a crowded space which is either a complete metric space of cardinality
![]() $\mathfrak c$
or second-countable locally compact Hausdorff. Then for each nonzero
$\mathfrak c$
or second-countable locally compact Hausdorff. Then for each nonzero
![]() $n<\omega $
there is a subalgebra of
$n<\omega $
there is a subalgebra of
![]() $\mathbf {Baire}(X)$
containing all clopen elements such that
$\mathbf {Baire}(X)$
containing all clopen elements such that
![]() $\mathsf {S5}_n$
is sound and strongly complete for
$\mathsf {S5}_n$
is sound and strongly complete for
![]() $\mathbf {Baire}(X)$
.
$\mathbf {Baire}(X)$
.
6 New completeness results for
 $\mathsf {S5U}$
$\mathsf {S5U}$
In this final section, we extend our completeness results to the language with the universal modality (recall that the latter can be interpreted in arbitrary algebraic models as per Definition 2.5). As in the previous section, these results utilize standard Kripke completeness results. In particular, the following completeness result is well known (see, e.g., [Reference Goranko and Passy15]), and can be lifted to strong completeness via standard methods.
Theorem 6.1.
![]() $\mathsf {S5U}$
is sound and strongly complete for the class of countable
$\mathsf {S5U}$
is sound and strongly complete for the class of countable
![]() $\mathsf {S5}$
-frames.
$\mathsf {S5}$
-frames.
In the topological setting, the language
![]() ${\mathcal L}^{}_{\Diamond \forall }$
is able to express connectedness by Shehtman’s axiom
${\mathcal L}^{}_{\Diamond \forall }$
is able to express connectedness by Shehtman’s axiom
(see [Reference Shehtman27]). Therefore,
![]() $\mathsf {S4U}$
is not complete for any connected space. The situation is quite different in the setting of Baire algebras, and in order to see this, we will need to discuss disconnectedness in this context. This notion has already been considered in the context of closure algebras by McKinsey and Tarski [Reference McKinsey and Tarski24].
$\mathsf {S4U}$
is not complete for any connected space. The situation is quite different in the setting of Baire algebras, and in order to see this, we will need to discuss disconnectedness in this context. This notion has already been considered in the context of closure algebras by McKinsey and Tarski [Reference McKinsey and Tarski24].
Definition 6.2. A closure algebra
![]() $(B,\mathbf {c})$
is disconnected if there are open
$(B,\mathbf {c})$
is disconnected if there are open
![]() $a,b \in B$
such that
$a,b \in B$
such that
![]() $a,b \not = 0$
,
$a,b \not = 0$
,
![]() $a \wedge b = 0$
, and
$a \wedge b = 0$
, and
![]() $ a \vee b = 1$
.
$ a \vee b = 1$
.
Lemma 6.3. If X is a Hausdorff Baire space with at least two points, then
![]() $\mathbf {Baire}(X)$
is disconnected.
$\mathbf {Baire}(X)$
is disconnected.
Proof Let
![]() $x\not = y$
in X, and let
$x\not = y$
in X, and let
![]() $U,V$
be the disjoint open neighborhoods of
$U,V$
be the disjoint open neighborhoods of
![]() $x,y$
. Set
$x,y$
. Set
![]() $a = [U]$
. Since U is open, a is open, hence clopen in
$a = [U]$
. Since U is open, a is open, hence clopen in
![]() $\mathbf {Baire}(X)$
. Because X is a Baire space, U is non-meager, so
$\mathbf {Baire}(X)$
. Because X is a Baire space, U is non-meager, so
![]() $a\ne 0$
. Also,
$a\ne 0$
. Also,
![]() $X\setminus U$
is non-meager because
$X\setminus U$
is non-meager because
![]() $V\subseteq X\setminus U$
. Thus,
$V\subseteq X\setminus U$
. Thus,
![]() $a\ne 1$
, and hence
$a\ne 1$
, and hence
![]() $\mathbf {Baire}(X)$
is disconnected.
$\mathbf {Baire}(X)$
is disconnected.
As was the case with resolvability, disconnectedness readily extends to
![]() $\kappa $
-disconnectedness for any cardinal
$\kappa $
-disconnectedness for any cardinal
![]() $\kappa $
.
$\kappa $
.
Definition 6.4. A closure algebra
![]() $(B,\mathbf {c})$
is
$(B,\mathbf {c})$
is
![]() $\kappa $
-disconnected if there is a sequence
$\kappa $
-disconnected if there is a sequence
![]() $(a_\iota )_{\iota <\kappa } \subseteq B$
of nonzero pairwise orthogonal clopen elements such that
$(a_\iota )_{\iota <\kappa } \subseteq B$
of nonzero pairwise orthogonal clopen elements such that
![]() $\bigvee _{\iota < \kappa } a_\iota = 1$
.
$\bigvee _{\iota < \kappa } a_\iota = 1$
.
Lemma 6.5. If X is an infinite Hausdorff Baire space, then
![]() $\mathbf {Baire}(X)$
is
$\mathbf {Baire}(X)$
is
![]() $\omega $
-disconnected.
$\omega $
-disconnected.
Proof First suppose that X has no limit points. Then every point is isolated, so each singleton
![]() $\{x_i\}$
is open, hence clopen and non-meager. Since X is infinite, we can choose a sequence of distinct points
$\{x_i\}$
is open, hence clopen and non-meager. Since X is infinite, we can choose a sequence of distinct points
![]() $(x_i)_{i < \omega }$
. Let
$(x_i)_{i < \omega }$
. Let
![]() $a_0 = [ X \setminus \{x_i\}_{1 \leq i<\omega } ] $
and for
$a_0 = [ X \setminus \{x_i\}_{1 \leq i<\omega } ] $
and for
![]() $i>0$
let
$i>0$
let
![]() $a_i = [ \{x_i\} ] $
. Then
$a_i = [ \{x_i\} ] $
. Then
![]() $(a_i)_{i<\omega }$
is a sequence of nonzero pairwise orthogonal clopens of
$(a_i)_{i<\omega }$
is a sequence of nonzero pairwise orthogonal clopens of
![]() $\mathbf {Baire}(X)$
, witnessing that X is
$\mathbf {Baire}(X)$
, witnessing that X is
![]() $\omega $
-disconnected.
$\omega $
-disconnected.
Next suppose that X has a limit point, say
![]() $x_\ast $
. We define a sequence of points
$x_\ast $
. We define a sequence of points
![]() $(x_i)_{ i <\omega }$
and two sequences of open sets
$(x_i)_{ i <\omega }$
and two sequences of open sets
![]() $(U_i)_{i \leq n}$
and
$(U_i)_{i \leq n}$
and
![]() $(V_i)_{ i \leq n}$
as follows.
$(V_i)_{ i \leq n}$
as follows.
To begin, choose
![]() $x_0 \not = x_\ast $
, and let
$x_0 \not = x_\ast $
, and let
![]() $U_0,V_0$
be disjoint open neighborhoods of
$U_0,V_0$
be disjoint open neighborhoods of
![]() $x_0,x_\ast $
, respectively. For the inductive step, suppose that
$x_0,x_\ast $
, respectively. For the inductive step, suppose that
![]() $(x_i)_{ i \leq n}$
,
$(x_i)_{ i \leq n}$
,
![]() $(U_i)_{ i \leq n}$
,
$(U_i)_{ i \leq n}$
,
![]() $(V_i)_{ i \leq n}$
are already chosen and satisfy the following conditions:
$(V_i)_{ i \leq n}$
are already chosen and satisfy the following conditions:
-
1. for all
 $i \leq n$
, we have
$i \leq n$
, we have
 $x_i \in U_i$
,
$x_i \in U_i$
,
 $x_\ast \in V_i$
, and
$x_\ast \in V_i$
, and
 $U_i$
,
$U_i$
,
 $V_i$
are open;
$V_i$
are open; -
2. if
 $i<j \leq n$
, then
$i<j \leq n$
, then
 $U_i\cap U_j = \varnothing $
, and
$U_i\cap U_j = \varnothing $
, and -
3. if
 $i\leq j \leq n$
, then
$i\leq j \leq n$
, then
 $U_i\cap V_j = \varnothing $
.
$U_i\cap V_j = \varnothing $
.
Since
![]() $x_\ast $
is a limit point, choose
$x_\ast $
is a limit point, choose
![]() $x_{n+1} \in V_{n}\setminus \{x_\ast \}$
. Let
$x_{n+1} \in V_{n}\setminus \{x_\ast \}$
. Let
![]() $U,V$
be disjoint neighborhoods of
$U,V$
be disjoint neighborhoods of
![]() $x_{n+1}, x_\ast $
, respectively, and define
$x_{n+1}, x_\ast $
, respectively, and define
![]() $U_{n+1} = U\cap V_n$
,
$U_{n+1} = U\cap V_n$
,
![]() $V_{n + 1} = V \cap V _n $
. It is not hard to check that the sequences
$V_{n + 1} = V \cap V _n $
. It is not hard to check that the sequences
![]() $(x_i)_{ i \leq n+1}$
,
$(x_i)_{ i \leq n+1}$
,
![]() $(U_i)_{ i \leq n+1}$
,
$(U_i)_{ i \leq n+1}$
,
![]() $(V_i)_{i \leq n+1}$
satisfy all the desired properties.
$(V_i)_{i \leq n+1}$
satisfy all the desired properties.
Once we have constructed
![]() $(U_i)_{i < \omega }$
, we let
$(U_i)_{i < \omega }$
, we let
![]() $a_0 = [X\setminus \bigcup _{1\leq n<\omega } U_n]$
and for
$a_0 = [X\setminus \bigcup _{1\leq n<\omega } U_n]$
and for
![]() $i>0$
we let
$i>0$
we let
![]() $a_i = [U_i]$
. Then
$a_i = [U_i]$
. Then
![]() $(a_i)_{i<\omega }$
is the desired sequence of nonzero pairwise orthogonal clopens of
$(a_i)_{i<\omega }$
is the desired sequence of nonzero pairwise orthogonal clopens of
![]() $\mathbf {Baire}(X)$
.
$\mathbf {Baire}(X)$
.
Remark 6.6. By Lemma 6.5, the Baire algebra of the Cantor space is
![]() $\omega $
-disconnected. In contrast, the Cantor space, while disconnected, is not
$\omega $
-disconnected. In contrast, the Cantor space, while disconnected, is not
![]() $\omega $
-disconnected because, by compactness, any partition into disjoint open sets must be finite. More generally, no compact space can be
$\omega $
-disconnected because, by compactness, any partition into disjoint open sets must be finite. More generally, no compact space can be
![]() $\omega $
-disconnected.
$\omega $
-disconnected.
Remark 6.7. Let X be an infinite separable Hausdorff Baire space. Then
![]() $\mathbf {Baire}(X)$
is
$\mathbf {Baire}(X)$
is
![]() $\omega $
-disconnected by Lemma 6.5. On the other hand,
$\omega $
-disconnected by Lemma 6.5. On the other hand,
![]() $\mathbf {Baire}(X)$
is not
$\mathbf {Baire}(X)$
is not
![]() $\kappa $
-disconnected for any cardinal
$\kappa $
-disconnected for any cardinal
![]() $\kappa> \omega $
. For, suppose that
$\kappa> \omega $
. For, suppose that
![]() $(a_i)_{i<\kappa } \subseteq \mathbf {Baire}(X)$
are pairwise orthogonal and clopen. Then for each
$(a_i)_{i<\kappa } \subseteq \mathbf {Baire}(X)$
are pairwise orthogonal and clopen. Then for each
![]() $i <\kappa $
, there is an open set
$i <\kappa $
, there is an open set
![]() $A_i\subseteq X$
with
$A_i\subseteq X$
with
![]() $a_i = [A_i]$
. We must have that
$a_i = [A_i]$
. We must have that
![]() $A_i \cap A_j = \varnothing $
if
$A_i \cap A_j = \varnothing $
if
![]() $i\not = j$
, for otherwise their intersection, being open, would be non-meager. It follows that
$i\not = j$
, for otherwise their intersection, being open, would be non-meager. It follows that
![]() $\kappa \le \omega $
as no separable space admits an uncountable collection of disjoint open subsets.
$\kappa \le \omega $
as no separable space admits an uncountable collection of disjoint open subsets.
Theorem 6.8. Let X be a Baire space and W an
![]() $\mathsf {S5}$
-frame with the upper cluster size
$\mathsf {S5}$
-frame with the upper cluster size
![]() $\lambda $
and the number of clusters
$\lambda $
and the number of clusters
![]() $\kappa $
. If
$\kappa $
. If
![]() $\mathbf {Baire}(X)$
is
$\mathbf {Baire}(X)$
is
![]() $\kappa $
-disconnected and
$\kappa $
-disconnected and
![]() $\lambda $
-resolvable, then there is an embedding
$\lambda $
-resolvable, then there is an embedding
![]() $h\colon {\mathbf {Kur}}(W) \to \mathbf {Baire}(X)$
.
$h\colon {\mathbf {Kur}}(W) \to \mathbf {Baire}(X)$
.
Proof Let
![]() $(C^\iota )_{\iota <\kappa }$
enumerate the clusters of W and let
$(C^\iota )_{\iota <\kappa }$
enumerate the clusters of W and let
![]() $\lambda _\iota = |C^\iota |$
. Enumerate each
$\lambda _\iota = |C^\iota |$
. Enumerate each
![]() $C^\iota $
by
$C^\iota $
by
![]() $( w^\iota _\nu ) _{\nu < \lambda _\iota }$
. Since
$( w^\iota _\nu ) _{\nu < \lambda _\iota }$
. Since
![]() $\mathbf {Baire}(X)$
is
$\mathbf {Baire}(X)$
is
![]() $\kappa $
-disconnected, there are pairwise orthogonal elements
$\kappa $
-disconnected, there are pairwise orthogonal elements
![]() $([U^\iota ])_{\iota < \kappa }$
such that each
$([U^\iota ])_{\iota < \kappa }$
such that each
![]() $U^\iota $
is open and
$U^\iota $
is open and
![]() $\bigsqcup _{\iota < \kappa } [U^\iota ] = [X]$
. Because X is a Baire space, the
$\bigsqcup _{\iota < \kappa } [U^\iota ] = [X]$
. Because X is a Baire space, the
![]() $U^\iota $
must be pairwise disjoint as their intersection is open and meager. By Lemma 4.6, for each
$U^\iota $
must be pairwise disjoint as their intersection is open and meager. By Lemma 4.6, for each
![]() $\iota < \kappa $
and
$\iota < \kappa $
and
![]() $\nu < \lambda _\iota $
, there are
$\nu < \lambda _\iota $
, there are
![]() $A^\iota _\nu \subseteq U^\iota $
that Baire
$A^\iota _\nu \subseteq U^\iota $
that Baire
![]() $\lambda _\iota $
-resolve
$\lambda _\iota $
-resolve
![]() $U^\iota $
.
$U^\iota $
.
Define a partial function
![]() $f\colon X \to W$
by
$f\colon X \to W$
by
![]() $f (x) = w$
if there exist
$f (x) = w$
if there exist
![]() $\iota < \kappa $
,
$\iota < \kappa $
,
![]() $\nu < \lambda _\iota $
such that
$\nu < \lambda _\iota $
such that
![]() $x \in A^\iota _\nu $
and
$x \in A^\iota _\nu $
and
![]() $w = w^\iota _\nu $
. We show that f is a Baire map. It is Baire-continuous since if
$w = w^\iota _\nu $
. We show that f is a Baire map. It is Baire-continuous since if
![]() $ V \subseteq W$
is open, then V is a union of clusters
$ V \subseteq W$
is open, then V is a union of clusters
![]() $\bigcup _{\iota \in I} C^\iota $
, hence
$\bigcup _{\iota \in I} C^\iota $
, hence
![]() $f^{-1}(V) = \bigcup _{\iota \in I} f^{-1} (C^\iota ) = \bigcup _{\iota \in I} U^{\iota }$
. It is Baire-open since if
$f^{-1}(V) = \bigcup _{\iota \in I} f^{-1} (C^\iota ) = \bigcup _{\iota \in I} U^{\iota }$
. It is Baire-open since if
![]() $V\subseteq X $
is nonempty open,
$V\subseteq X $
is nonempty open,
![]() $M\subseteq X$
meager, and
$M\subseteq X$
meager, and
![]() $w\in f(V\setminus M)$
, then
$w\in f(V\setminus M)$
, then
![]() $ w = w^\iota _\nu $
for some
$ w = w^\iota _\nu $
for some
![]() $\iota $
,
$\iota $
,
![]() $\nu $
. Since
$\nu $
. Since
![]() $V\cap U^\iota \neq \varnothing $
and the sets
$V\cap U^\iota \neq \varnothing $
and the sets
![]() $A^\iota _{\nu '}$
yield a Baire
$A^\iota _{\nu '}$
yield a Baire
![]() $\lambda _\iota $
-resolution of
$\lambda _\iota $
-resolution of
![]() $U^\iota $
, we have that
$U^\iota $
, we have that
![]() $A^\iota _{\nu '} \cap V $
is non-meager for any
$A^\iota _{\nu '} \cap V $
is non-meager for any
![]() $\nu ' < \lambda _\iota $
. Therefore,
$\nu ' < \lambda _\iota $
. Therefore,
![]() $(A^\iota _{\nu '} \cap V)\setminus M$
is nonempty, and hence
$(A^\iota _{\nu '} \cap V)\setminus M$
is nonempty, and hence
![]() $w^\iota _{\nu '} \in f(V\setminus M) $
. Since
$w^\iota _{\nu '} \in f(V\setminus M) $
. Since
![]() $\nu '$
was arbitrary,
$\nu '$
was arbitrary,
![]() $C^\iota \subseteq f(V\setminus M)$
, and since
$C^\iota \subseteq f(V\setminus M)$
, and since
![]() $w$
was arbitrary,
$w$
was arbitrary,
![]() $f(V\setminus M)$
is open, hence f is Baire-open. The map f is defined almost everywhere since
$f(V\setminus M)$
is open, hence f is Baire-open. The map f is defined almost everywhere since
![]() $[X] = \bigsqcup _{\iota <\kappa } [U^\iota ]$
, so
$[X] = \bigsqcup _{\iota <\kappa } [U^\iota ]$
, so
![]() $X\setminus \bigcup _{\iota <\kappa } U^\iota $
is meager. It is trivially non-degenerate since the only meager subset of W is the empty set. Finally, it is exact by Lemma 5.8 since
$X\setminus \bigcup _{\iota <\kappa } U^\iota $
is meager. It is trivially non-degenerate since the only meager subset of W is the empty set. Finally, it is exact by Lemma 5.8 since
![]() $f^{-1}(w^\iota _\nu ) = A^\iota _\nu $
, which is non-meager. Thus,
$f^{-1}(w^\iota _\nu ) = A^\iota _\nu $
, which is non-meager. Thus,
![]() $h\colon {\mathbf {Kur}}(W) \to \mathbf {Baire}(X)$
given by
$h\colon {\mathbf {Kur}}(W) \to \mathbf {Baire}(X)$
given by
![]() $h(B) = [f^{-1} (B)]$
is an embedding by Lemma 5.7.
$h(B) = [f^{-1} (B)]$
is an embedding by Lemma 5.7.
Theorem 6.9. If X is
![]() $\omega $
-resolvable, then
$\omega $
-resolvable, then
![]() $\mathsf {S5U}$
is sound and strongly complete for
$\mathsf {S5U}$
is sound and strongly complete for
![]() $\mathbf {Baire}(X)$
.
$\mathbf {Baire}(X)$
.
Proof Soundness follows from
![]() $\mathbf {Baire}(X)$
being a monadic algebra. For completeness, if
$\mathbf {Baire}(X)$
being a monadic algebra. For completeness, if
![]() $\Gamma \not \vdash _{\mathsf {S5U}} \varphi $
, then by Theorem 6.1, there is a countable
$\Gamma \not \vdash _{\mathsf {S5U}} \varphi $
, then by Theorem 6.1, there is a countable
![]() $\mathsf {S5}U$
-frame W and a valuation
$\mathsf {S5}U$
-frame W and a valuation ![]() such that
such that
![]() $\Gamma \not \models _{W} \varphi $
. By Theorem 6.8, there is an embedding
$\Gamma \not \models _{W} \varphi $
. By Theorem 6.8, there is an embedding
![]() $f\colon \mathbf {Kur} (W) \to \mathbf {Baire}(X)$
. Thus,
$f\colon \mathbf {Kur} (W) \to \mathbf {Baire}(X)$
. Thus,
![]() $\Gamma \not \models _{\mathbf {Baire}(X)} \varphi $
.
$\Gamma \not \models _{\mathbf {Baire}(X)} \varphi $
.
Corollary 6.10. Let X be a crowded space which is either completely metrizable and of cardinality continuum or locally compact Hausdorff. Then
![]() $\mathsf {S5U}$
is sound and strongly complete for
$\mathsf {S5U}$
is sound and strongly complete for
![]() $\mathbf {Baire}(X)$
. In particular,
$\mathbf {Baire}(X)$
. In particular,
![]() $\mathsf {S5U}$
is sound and strongly complete for
$\mathsf {S5U}$
is sound and strongly complete for
![]() $\mathbf {Baire}(\mathbb R)$
and
$\mathbf {Baire}(\mathbb R)$
and
![]() $\mathbf {Baire}(\mathbf {C})$
, where
$\mathbf {Baire}(\mathbf {C})$
, where
![]() $\mathbf {C}$
is the Cantor space.
$\mathbf {C}$
is the Cantor space.
Corollary 6.10 can be viewed as an analogue of the McKinsey–Tarski theorem for
![]() $\mathsf {S5U}$
. As mentioned in Remark 5.13, a similar result does not hold for
$\mathsf {S5U}$
. As mentioned in Remark 5.13, a similar result does not hold for
![]() $\mathbb Q$
, even though
$\mathbb Q$
, even though
![]() $\mathsf {S4U}$
is complete for
$\mathsf {S4U}$
is complete for
![]() $\mathbb Q$
but not
$\mathbb Q$
but not
![]() $\mathbb R$
(see, e.g., [Reference Shehtman27]), so the picture in the Baire setting is a bit different from the original topological semantics.
$\mathbb R$
(see, e.g., [Reference Shehtman27]), so the picture in the Baire setting is a bit different from the original topological semantics.
Remark 6.11. Corollary 6.10 does not extend to uncountable languages in view of Remark 6.7 as the collection
cannot be satisfied on, e.g., the real line if
![]() $\kappa>\omega $
since this would require
$\kappa>\omega $
since this would require ![]() with disjoint open sets
with disjoint open sets
![]() $U_\iota $
, which is impossible on
$U_\iota $
, which is impossible on
![]() $\mathbb R$
.
$\mathbb R$
.
7 Concluding remarks
We have shown that the Baire algebra of any topological space is a closure algebra, and that the logic of these algebras is
![]() $\mathsf {S5}$
, providing variants of the celebrated McKinsey–Tarski theorem for the logic
$\mathsf {S5}$
, providing variants of the celebrated McKinsey–Tarski theorem for the logic
![]() $\mathsf {S5}$
. We have identified Baire resolvability as a sufficient condition for strong completeness. For such spaces, we have also constructed subalgebras of the Baire algebra whose logic is
$\mathsf {S5}$
. We have identified Baire resolvability as a sufficient condition for strong completeness. For such spaces, we have also constructed subalgebras of the Baire algebra whose logic is
![]() $\mathsf {S5}_n$
(for any finite n). Given a cardinal
$\mathsf {S5}_n$
(for any finite n). Given a cardinal
![]() $\lambda $
, strong completeness also holds for variants of
$\lambda $
, strong completeness also holds for variants of
![]() $\mathsf {S5}$
with
$\mathsf {S5}$
with
![]() $\lambda $
-many variables provided that the space is Baire
$\lambda $
-many variables provided that the space is Baire
![]() $\lambda $
-resolvable. In addition, we have shown that if the Baire algebra is
$\lambda $
-resolvable. In addition, we have shown that if the Baire algebra is
![]() $\omega $
-disconnected, then strong completeness extends to
$\omega $
-disconnected, then strong completeness extends to
![]() $\mathsf {S5U}$
. Finally, we have shown that crowded spaces which are either complete continuum-sized metric or locally compact Hausdorff enjoy the above properties, leading to a large class of concrete examples of spaces for which
$\mathsf {S5U}$
. Finally, we have shown that crowded spaces which are either complete continuum-sized metric or locally compact Hausdorff enjoy the above properties, leading to a large class of concrete examples of spaces for which
![]() $\mathsf {S5}$
and
$\mathsf {S5}$
and
![]() $\mathsf {S5U}$
are strongly complete.
$\mathsf {S5U}$
are strongly complete.
This work follows [Reference Fernández-Duque12, Reference Lando22] in studying point-free semantics for modal logic based on quotients of the powerset algebras of topological spaces. There are many other
![]() $\sigma $
-ideals that may be used to define similar quotients, e.g., the
$\sigma $
-ideals that may be used to define similar quotients, e.g., the
![]() $\sigma $
-ideal of countable subsets. A general and systematic study of such quotients and their associated modal logics remains an interesting line of research.
$\sigma $
-ideal of countable subsets. A general and systematic study of such quotients and their associated modal logics remains an interesting line of research.
Acknowledgements
We are grateful to Jan van Mill for fruitful discussion and many useful suggestions. This included drawing our attention to the Disjoint Refinement Lemma—our main tool in Section 4. We would also like to thank the referees whose comments have considerably improved the paper.
Funding
David Fernández-Duque was supported by the FWO–FWF Lead Agency (Grant No. G030620N (FWO)/I4513N (FWF)) and by the SNSF–FWO Lead Agency (Grant No. 200021L_196176/G0E2121N).