No CrossRef data available.
Article contents
An extension of Ackermann's set theory
Published online by Cambridge University Press: 12 March 2014
Extract
Ackermann's set theory [1], called here A, involves a schema

where φ is an ∈-formula with free variables among y1, …, yn and w does not appear in φ. Variables are thought of as ranging over classes and V is intended as the class of all sets.
S is a kind of comprehension principle, perhaps most simply motivated by the following idea: The familiar paradoxes seem to arise when the class CP of all P-sets is claimed to be a set, while there exists some P-object x not in CP such that x would have to be a set if CP were. Clearly this cannot happen if all P-objects are sets.
Now, Levy [2] and Reinhardt [3] showed that A* (A with regularity) is in some sense equivalent to ZF. But the strong replacement axiom of Gödel-Bernays set theory intuitively ought to be a theorem of A* although in fact it is not (Levy's work shows this). Strong replacement can be formulated as
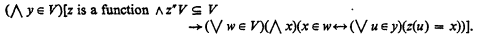
This lack of A* can be remedied by replacing S above by

where ψ and φ are ∈-formulas and x is not in ψ and w is not in φ. ψv is ψ with quantifiers relativized to V, and y and z stand for y1, …, yn and z1, …, zm.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972


