Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T21:58:25.327Z Has data issue: false hasContentIssue false
  • English
  • Français

An algebraic result about soft model theoretical equivalence relations with an application to H. Friedman's fourth problem

Published online by Cambridge University Press:  12 March 2014

Daniele Mundici
Daniele Mundici*
Affiliation:
Loc. Romola N. 76, 50060 Donnini, Florence, Italy
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the following algebraic characterization of elementary equivalence: ≡ restricted to countable structures of finite type is minimal among the equivalence relations, other than isomorphism, which are preserved under reduct and renaming and which have the Robinson property; the latter is a faithful adaptation for equivalence relations of the familiar model theoretical notion. We apply this result to Friedman's fourth problem by proving that if 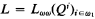is an (ω1, ω)-compact logic satisfying both the Robinson consistency theorem on countable structures of finite type and the Löwenheim-Skolem theorem for some λ < ωω for theories having ω1 many sentences, then ≡L = ≡ on such structures.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 46 , Issue 3 , September 1981 , pp. 523 - 530
Copyright
Copyright © Association for Symbolic Logic 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ba]Barwise, K.J., Axioms for abstract model theory, Annals of Mathematical Logic, vol. 7 (1974), pp. 221–265.CrossRefGoogle Scholar
[BKM]Barwise, K.J., Kaufmann, M. and Makkai, M., Stationary logic, Annals of Mathematical Logic, vol. 13 (1978), pp. 171–224.CrossRefGoogle Scholar
[Fe]Feferman, S., Two notes on abstract model theory. I, Fundament a Mathematicae, vol. 82 (1974), pp. 153–165 and II, Fundament a Mathematicae, vol. 89 (1975), pp. 111–130.CrossRefGoogle Scholar
[Fl]Flum, J., First order logic and its extensions, Lecture Notes in Mathematics, no. 499, Springer, Berlin, 1976, pp. 248–310.Google Scholar
[Fr]Friedman, H., One hundred and two problems in mathematical logic, this Journal, vol. 40 (1975), pp. 113–129.Google Scholar
[Ke]Keisler, H.J., Constructions in model theory, CIME II Ciclo, Coord. Mangani, Model theory and applications, Cremonese, Rome, 1975.Google Scholar
[MSI]Makowsky, J.A. and Shelah, S., The theorems of Beth and Craig in abstract model theory. I: The abstract setting, Transactions of the American Mathematical Society, vol. 256(1979), pp. 215–239.Google Scholar
[MS2]Makowsky, J.A. and Shelah, S., Positive results in abstract model theory: A theory of compact logics (to appear).Google Scholar
[MSS]Makowsky, J. A., Shelah, S. and Stavi, J., ⊿-logics and generalized quantifiers, Annals of Mathematical Logic, vol. 10(1976),pp. 155–192.CrossRefGoogle Scholar
[Mul]Mundici, D., Compactness + Craig interpolation = Robinson consistency in any logic (preprint).Google Scholar
[Mu2]Mundici, D., Compactness = JEP in any logic, Fundamenta Mathematicae (to appear).Google Scholar
[Mu3]Mundici, D., Compactness, interpolation and Friedman's third problem (to appear).Google Scholar
[Mu4]Mundici, D., Applications of many-sorted Robinson consistency theorem, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik (to appear).Google Scholar
[Mu5]Mundici, D., Robinson's consistency theorem in soft model theory, Transactions of the American Mathematical Society (to appear).Google Scholar