Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Koszmider, Piotr
1995.
Semimorasses and nonreflection at singular cardinals.
Annals of Pure and Applied Logic,
Vol. 72,
Issue. 1,
p.
1.
Kanamori, Akihiro
2011.
Kunen and set theory.
Topology and its Applications,
Vol. 158,
Issue. 18,
p.
2446.
Bagaria, Joan
2024.
The relative strengths of fragments of Martin's axiom.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 1,
p.
103330.


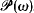 .
.