Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-06T03:48:31.114Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal spaces for classes of scattered eberlein compact spaces

Published online by Cambridge University Press:  12 March 2014

Murray Bell  and
Witold Marciszewski
Murray Bell
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg, R3T 2N2, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

We discuss the existence of universal spaces (either in the sense of embeddings or continuous images) for some classes of scattered Eberlein compacta. Given a cardinal κ, we consider the class δκof all scattered Eberlein compact spaces K of weight ≤ κ and such that the second Cantor-Bendixson derivative of K is a singleton. We prove that if κ is an uncountable cardinal such that κ = 2≤κ, then there exists a space X in δκ such that every member of δκ is homeomorphic to a retract of X. We show that it is consistent that there does not exist a universal space (either by embeddings or by mappings onto) in 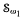. Assuming that 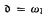= ω1, we prove that there exists a space X ∈ 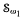which is universal in the sense of embeddings. We also show that it is consistent that there exists a space X bΕ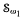, universal in the sense of embeddings, but δω1 does not contain an universal element in the sense of mappings onto.

Keywords

compact spacescatteredEberleinUniform Eberleinuniversal
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 71 , Issue 3 , September 2006 , pp. 1073 - 1080
Copyright
Copyright © Association for Symbolic Logic 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Alster, K., Almost disjoint families and some characterizations of alephs, Bulletin of the Polish Academy of Sciences, vol. 25 (1977), pp. 1203–1206.Google Scholar
[2]Alster, K., Some remarks on Eberlein compacts, Fundament a Mathematicae, vol. 104 (1979), pp. 43–46.CrossRefGoogle Scholar
[3]Argyros, S. and Benyamini, Y., Universal WCG Banach spaces and universal Eberlein compacts, Israel Journal of Mathematics, vol. 58 (1987), pp. 305–320.CrossRefGoogle Scholar
[4]Bell, J. L. and Slomson, A. B., Models and ultraproducts: an introduction, North-Holland Publishing Co., Amsterdam-London, 1969.Google Scholar
[5]Bell, M., Universal uniform Eberlein compact spaces, Proceedings of the American Mathematical Society, vol. 128 (2000), pp. 2191–2197.CrossRefGoogle Scholar
[6]Bell, M. and Marciszewski, W., On scattered Eberlein compact spaces, Israel Journal of Mathematics, (to appear).Google Scholar
[7]Chang, C. C. and Keisler, H. J., Model theory, third ed., Studies in Logic and the Foundations of Mathematics, vol. 73, North-Holland Publishing Co., Amsterdam, 1990.Google Scholar
[8]Džamonja, M., On uniform Eberlein compacta and c-algebras, Topology Proceedings, vol. 23 (1998), pp. 143–150.Google Scholar
[9]Džamonja, M., Universality of uniform Eberlein compacta, Proceedings of the American Mathematical Society, vol. 134 (2006), pp. 2427–2435.CrossRefGoogle Scholar
[10]Fleischer, I., A note on Universal Homogeneous Models, Mathematica Scandinavica, vol. 19 (1966), pp. 183–184.CrossRefGoogle Scholar
[11]Fleischer, I., Concerning my note on Universal Homogeneous Models, Mathematica Scandinavica, vol. 38 (1976), p. 24.CrossRefGoogle Scholar
[12]Jonsson, B., Universal relational systems, Mathematica Scandinavica, vol. 4 (1956), pp. 193–208.CrossRefGoogle Scholar
[13]Koiman, M. and Shelah, S., Nonexistence of universal orders in many cardinals, this Journal, vol. 57 (1992), no. 3, pp. 875–891.Google Scholar
[14]Marciszewski, W., On Banach spaces C(K) isomorphic to c0(Γ), Studia Mathematica, vol. 156 (2003), pp. 295–302.CrossRefGoogle Scholar
[15]Morley, M. and Vaught, R., Homogeneous universal models, Mathematica Scandinavica, vol. 11 (1962), pp. 37–57.CrossRefGoogle Scholar
[16]Douwen, E. Van, The integers and topology, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J., editors), North-Holland, 1984, pp. 111–167.CrossRefGoogle Scholar