Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T15:07:15.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Truth definitions in finite models

Published online by Cambridge University Press:  12 March 2014

Leszek Aleksander Kołodziejczyk
Leszek Aleksander Kołodziejczyk*
Affiliation:
Institute of Philosophy, Warsaw University, Krakowskie Przedmieście 3, 00-047 Warsaw, Poland, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper discusses the notion of finite model truth definitions (or FM-truth definitions), introduced by M. Mostowski as a finite model analogue of Tarski's classical notion of truth definition.

We compare FM-truth definitions with Vardi's concept of the combined complexity of logics, noting an important difference: the difficulty of defining FM-truth for a logic 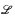does not depend on the syntax of 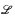, as long as it is decidable. It follows that for a natural 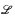there exist FM-truth definitions whose evaluation is much easier than the combined complexly of 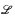would suggest.

We apply the general theory to give a complexity-theoretical characterization of the logics for which the 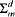classes (prenex classes of higher order logics) define FM-truth. For any d ≥ 2, m ≥ 1 we construct a family 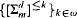of syntactically defined fragments of 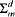which satisfy this characterization. We also use the 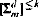classes to give a refinement of known results on the complexity classes captured by .

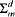We close with a few simple corollaries, one of which gives a sufficient condition for the existence, given a vocabulary σ, of a fixed number k such that model checking for all first order sentences over σ can be done in deterministic time nk.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 1 , March 2004 , pp. 183 - 200
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balcázar, J. L., Díaz, J., and Gabarró, J., Structural complexity I, second, revised ed., Springer-Verlag, 1995.CrossRefGoogle Scholar
[2]Bennett, J., On spectra, Ph. D. Thesis, Princeton University, 1962.Google Scholar
[3]Börger, E., Decision problems in predicate logic, Logic colloquium '82 (Lolli, G.et al., editors), North-Holland, 1984, pp. 263–301.Google Scholar
[4]Christen, C. A., Spektren und Klassen Elementarer Funktionen, Ph. D. Thesis, ETH Zürich, 1974.Google Scholar
[5]Eiter, T., Gottlob, G., and Gurevich, Y., Normal forms for second-order logic over finite structures, and classification of NP optimization problems, Annals of Pure and Applied Logic, vol. 78 (1996), pp. 111–125.CrossRefGoogle Scholar
[6]Fagin, R., Generalized first-order spectra and polynomial-time recognizable sets, Complexity of Computation, S1AM-AMS Proceedings, vol. 7 (1974), pp. 43–73.Google Scholar
[7]Gottlob, G., Relativized Logspace and generalized quantifiers over finite ordered structures, this Journal, vol. 62 (1997), pp. 545–574.Google Scholar
[8]Gottlob, G., Leone, N., and Veith, H., Succinctness as a source of complexity in logical formalisms, Annals of Pure and Applied Logic, vol. 97 (1999), pp. 231–260.Google Scholar
[9]Hella, L. and Torres, J. M. Turull, Expressing database queries with higher order logics, Technical Report 5/2003, Information Systems Department, Massey University, 2003.Google Scholar
[10]Immerman, N., Descriptive complexity, Springer-Verlag, 1999.CrossRefGoogle Scholar
[11]Leivant, D., Descriptive characterizations of computational complexity, Journal of Computer and System Sciences, vol. 39 (1987), pp. 51–83.CrossRefGoogle Scholar
[12]Leivant, D., Higher order logic, Handbook of logic in artificial intelligence and logic programming (Gabbay, D. M.et al., editors), vol. 2, Oxford University Press, 1994, pp. 228–321.Google Scholar
[13]Makowsky, J. A. and Pnueli, Y. B., Arity and alternation in second order logic, Annals of Pure and Applied Logic, vol. 78 (1996), pp. 189–202.Google Scholar
[14]Mostowski, M., On representing concepts infinite models, Mathematical Logic Quarterly, vol. 47 (2001). pp. 513–523.3.0.CO;2-J>CrossRefGoogle Scholar
[15]Mostowski, M., On representing semantics infinite models, to appear in Proceedings of Contributed Papers, LMPhSc 99.Google Scholar
[16]Stockmeyer, L., The polynomial-time hierarchy, Theoretical Computer Science, vol. 3 (1977). pp. 1–22.CrossRefGoogle Scholar
[17]Tarski, A., Pojȩcie prawdy w językach nauk dedukcyjnych, Warszawskie Towarzystwo Naukowe, Warszawa, 1933, English translation of the German version: The concept of truth in formalized languages, in A. Tarski. Logic, semantics, metamathematics, Oxford University Press. 1956. pp. 152–278.Google Scholar
[18]Vardi, M., The complexity of relational query languages, Proceedings of the 14th ACM Symposium on Theory of Computing, 1982, pp. 137–146.Google Scholar
[19]Zdanowski, K., Arithmetics in finite hut potentially infinite worlds, Ph. D. Thesis, Warsaw University, in preparation.Google Scholar