Published online by Cambridge University Press: 12 March 2014
Theorem. There is an effective procedure to decide whether the set of tautologies determined by a given truth-table with a finite number of elements is empty or not.
Proof. Let W(P) be a w.f.f. with a single variable P and 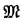 n a given n-valued truth-table with elements (values)
n a given n-valued truth-table with elements (values)

Substitute 1, 2, 3, …, n in succession for P. By the usual contraction process let W(P) assume the truth-values w1, w2, w3, …, wn respectively. The sequence
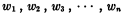
will be called the value sequence of W(P).
Value sequences consisting of designated elements of 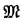 exclusively will be called designated; others will be called undesignated.
exclusively will be called designated; others will be called undesignated.
All the W(P)'s will be classified in the following way:
(a) to the first class CL1 of W(P)'s there belongs the one element P,
(b) to the (t + 1)th class CLt + 1 belong all the w.f.f. which can be built up by means of one generating connective from constituent w.f.f. of which one is an element of CLt and all the others (if any) are elements of CLn ≤ t.
For example, if N and C are the connectives described by a truth-table 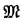

etc.
Let ∣CLn∣ stand for the set of value sequences of the elements of CLn.
1 See the author's Note on truth-tables, in this number of this Journal, and On Tarski's matrix method, forthcoming in the Comptes rendus des séances de la Société des Sciences et des Lettres de Varsovie.