It has been proved by Pepis that any formula of the first-order predicate calculus is equivalent (in respect of being satisfiable) to another with a prefix of the form

containing a single existential quantifier. In this paper, we shall improve this theorem in the like manner as the Ackermann and the Gödel reduction theorems have been improved in the preceding papers of the same main title. More explicitly, we shall prove the

Theorem 1. To any given first-order formula it is possible to construct an equivalent one with a prefix of the form (1) and a matrix containing no other predicate variable than a single binary one.

An analogous theorem, but producing a prefix of the form

has been proved in the meantime by Surányi; some modifications in the proof, suggested by Kalmár, led to the above form.

In this paper a method will be described which is intended to exhibit some relationships between sets of tautologies determined by truth-tables. This method is an attempt to form an algebra of truth-tables. The results sketched below are restricted to sets of tautologies determined by truth-tables with a finite number of elements and involving a single binary connective Δ. However, most of the results can be easily extended to the case of Tarski's logical matrix and even to a more general case.

We denote by S() the set of all tautologies (-tautologies) according to a given truth-table . Let describe a binary connective Δ. Then Δ()(x, y) stands for the truth-value of ΔPQ, when P has the truth-value x and Q has the truth-value y. If no ambiguity may arise we write Δ(x, y) or Δ() for Δ()(x, y).

Theorem. There is an effective procedure to decide whether the set of tautologies determined by a given truth-table with a finite number of elements is empty or not.

Proof. Let W(P) be a w.f.f. with a single variable P and 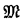n a given n-valued truth-table with elements (values)

Substitute 1, 2, 3, …, n in succession for P. By the usual contraction process let W(P) assume the truth-values w1, w2, w3, …, wn respectively. The sequence

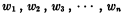
will be called the value sequence of W(P).

Value sequences consisting of designated elements of 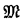exclusively will be called designated; others will be called undesignated.

All the W(P)'s will be classified in the following way:

(a) to the first class CL1 of W(P)'s there belongs the one element P,

(b) to the (t + 1)th class CLt + 1 belong all the w.f.f. which can be built up by means of one generating connective from constituent w.f.f. of which one is an element of CLt and all the others (if any) are elements of CLn ≤ t.

For example, if N and C are the connectives described by a truth-table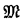

etc.

Let ∣CLn∣ stand for the set of value sequences of the elements of CLn.

The purpose of the present paper is to construct a fragment of number theory not subject to Gödel incompletability. Originally the system was designed as a metalanguage for classical mathematics (see section 10); but it now appears to the author worthwhile to present it as a mathematical system in its own right, to serve however rather as an instrument of computation than of proof. Its resources in the latter respect seem very extensive, sufficient apparently for the systematic tabulation of every function used in any but the most recondite physics. The author intends to pursue this topic in a later paper; the present one will simply present the system, along with proofs of consistency and completeness and a few metatheorems which will be used as lemmas for future research.

Completeness is achieved by sacrificing the notions of negation and universal quantification customary in number-theoretic systems; the losses consequent upon this are made good in part by the use of the ancestral as a primitive idea. The general outlines of the system follow closely the pattern of Fitch's “basic logic”; however the latter system uses combinatory operators in place of the variables used in the present paper, and if variables are introduced into Fitch's system by definition their range of values will be found to be much more extensive than that of my variables. The present system K is thus a weaker form of Fitch's system.

It is apparently not known whether or not Fitch's system is complete.

The object of this note is to classify the isomorphism types of all complete atomic proper relation algebras. In particular we find that the number of abstractly distinct complete atomic proper finite relation algebras of 2m elements is equal to the number of distinct partitions of the positive integer m into summands which are perfect squares.

A relation algebra is called complete atomic if its Boolean algebra is complete atomic. A proper relation algebra is a relation algebra whose elements are relations. Lyndon has recently proved, by constructing an appropriate finite relation algebra, that not every complete atomic relation algebra is isomorphic to a proper relation algebra.

Henceforth, let us consider a complete atomic proper relation algebra. The atoms {〈a, b〉}, {〈c, d〉} will be called connected if and only if {a, b} ⋂ {c, d} is not empty. Let the relation of connectedness over the set B of all atoms be denoted by ~. For brevity let B = {b1,b2, …}. The relation ~ is obviously reflexive and symmetric. But ~ is not transitive, since a, b, c, d distinct implies {〈a, 0〉} ~ {〈b, c〉}, {〈b, c〉} ~ {〈c, d〉}, and {〈a, b〉} ≁ {〈c, d〉}.