Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T05:28:06.059Z Has data issue: false hasContentIssue false
  • English
  • Français

The strength of admissibility without foundation

Published online by Cambridge University Press:  12 March 2014

Gerhard Jäger
Gerhard Jäger*
Affiliation:
Stanford University, Stanford, California 94305
*
Current address: Mathematisches Institut der Ludwig-Maximilians-Universität, D-8000 München 2, West Germany.
Get access Rights & Permissions [Opens in a new window]

Extract

The following is part of a series of papers on theories for (iterated) admissible sets (cf. [10], [11], [12], [14], [15]). Although these theories are weak subsystems of Zermelo-Fraenkel set theory, they allow one to formalize and prove a fair amount of definability theory and generalized recursion theory. Using this machinery it is in general not very hard to establish the connections between theories for admissible sets and (for example) systems of second order arithmetic. A proof-theoretic analysis of theories for admissible sets therefore provides quite a uniform and powerful framework for the proof-theoretic treatment of many systems of set theory, second order arithmetic and constructive mathematics (see [12] and [15]). The strongest result in this direction so far is the pair of proof-theoretic equivalences

where T0 is Feferman's system for explicit mathematics of [5] and [6], (-CA) + (BI) is the usual system of second order arithmetic with the axiom of -comprehension and bar induction and KPi is Kripke-Platek set theory with ∈-induction

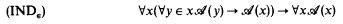
for arbitrary formulas and the additional axiom

.

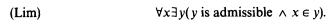The least standard model of KPi is L(i0) where i0 is the first recursively inaccessible ordinal.

In this paper we are mainly interested in the theory KPi0 which results from KPi by severely restricting the principles of induction. Basically, complete induction on the natural numbers

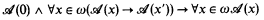
is allowed only for ∆0-formulas, and (IND∈) is omitted completely.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 3 , September 1984 , pp. 867 - 879
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barwise, J., Admissible sets and structures, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
[2]Buchholz, W., Feferman, S., Pohlers, W. and Sieg, W., Iterated inductive definitions and subsystems of analysis: Recent proof-theoretical studies, Lecture Notes in Mathematics, vol. 897, Springer-Verlag, Berlin, 1981.Google Scholar
[3]Cantini, A., A note on the theory of admissible sets with ∈-induction restricted to formulas with one quantifier and related systems (to appear).Google Scholar
[4]Feferman, S., Systems of predicative analysis, this Journal, vol. 29 (1964), pp. 1–30.Google Scholar
[5]Feferman, S., A language and axioms for explicit mathematics, Algebra and Logic (Summer Research Institute, Clayton, 1974), Lecture Notes in Mathematics, vol. 450, Springer-Verlag, 1975, pp. 87–139.CrossRefGoogle Scholar
[6]Feferman, S., Constructive theories of functions and classes, Logic Colloquium '78, North-Holland, Amsterdam, 1979, pp. 159–224.Google Scholar
[7]Feferman, S., Iterated inductive fixed-point theories: Application to Hancock's conjecture, Patras logic symposion (1980), North-Holland, Amsterdam, 1982, pp. 171–196.CrossRefGoogle Scholar
[8]Friedman, H., Iterated inductive definitions and -AC, Intuitionism and proof theory (Proceedings, Buffalo, New York, 1968), North-Holland, Amsterdam, 1970, pp. 435–442.Google Scholar
[9]Friedman, H., McAloon, K. and Simpson, S. G., A finite combinatorial principle which is equivalent to the 1-consistency of predicative analysis, Patras logic symposion (1980), North-Holland, Amsterdam, 1982, pp. 197–230.CrossRefGoogle Scholar
[10]Jäger, G., Beweistheorie von KPN, Archiv für Mathematische Logik und Grundlagenforschung, vol. 20 (1980), pp. 53–63.CrossRefGoogle Scholar
[11]Jäger, G., Zur Beweistheorie der Kripke-Platek Mengenlehre uber den natürlichen Zahlen, Archiv für Mathematische Logik und Grundlagenforschung, vol. 22 (1982), pp. 121–139.CrossRefGoogle Scholar
[12]Jäger, G., Iterating admissibility in proof theory, Proceedings of the Herbrand Symposium (Logic Colloquium '80), North-Holland, Amsterdam, 1982, pp. 137–146.CrossRefGoogle Scholar
[13]Jäger, G., A well-ordering proof for Feferman's theory T0, Archiv für Mathematische Logik und Grundlagenforschung, vol. 23 (1983), pp. 65–77.CrossRefGoogle Scholar
[14]Jäger, G., A version of Kripke-Platek set theory which is conservative over Peano arithmetic, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik (to appear).Google Scholar
[15]Jäger, G. and Pohlers, W., Eine beweistheoretische Untersuchung von (-CA) + (BI) und verwandter Systeme, Bayerische Akademie der Wissenschaften, Mathematisch-Naturwissenschaftliche Klasse: Sitzungsberichte, 1982, pp. 1–28.Google Scholar
[16]Martin-Löf, P., An intuitionistic theory of types: Predicative part, Logic Colloquium '73, North-Holland, Amsterdam, 1975, pp. 73–118.Google Scholar
[17]Pearce, J., Constructive cut elimination arguments and applications, Ph.D. thesis. University of California, Berkeley, California, 1980.Google Scholar
[18]Schütte, K., Proof theory, Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
[19]Simpson, S. G., and transfinite induction, Logic Colloquium '80, North-Holland, Amsterdam, 1982, pp. 239–253.Google Scholar
[20]Simpson, S. G., Set theoretic aspects of ATR0, Logic Colloquium '80, North-Holland, Amsterdam, 1982, pp. 255–271.Google Scholar
[21]Tait, W. W., Normal derivability in classical logic, The syntax and semantics of infinitary languages, Lecture Notes in Mathematics, vol. 72, Springer-Verlag, Berlin, 1968, pp. 204–236.CrossRefGoogle Scholar