Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Harizanov, Valentina S.
2002.
Computability-Theoretic Complexity of Countable Structures.
Bulletin of Symbolic Logic,
Vol. 8,
Issue. 4,
p.
457.
Frolov, A. N.
2006.
Δ 2 0 -copies of linear orderings.
Algebra and Logic,
Vol. 45,
Issue. 3,
p.
201.
Kalimullin, Iskander
2007.
Computation and Logic in the Real World.
Vol. 4497,
Issue. ,
p.
389.
Kalimullin, I. Sh.
2008.
Restrictions on the degree spectra of algebraic structures.
Siberian Mathematical Journal,
Vol. 49,
Issue. 6,
p.
1034.
Melnikov, Alexander G.
2009.
Enumerations and Completely Decomposable Torsion-Free Abelian Groups.
Theory of Computing Systems,
Vol. 45,
Issue. 4,
p.
897.
Csima, Barbara F.
and
Kalimullin, Iskander S.
2010.
Degree spectra and immunity properties.
Mathematical Logic Quarterly,
Vol. 56,
Issue. 1,
p.
67.
DOWNEY, ROD
LEMPP, STEFFEN
and
WU, GUOHUA
2010.
ON THE COMPLEXITY OF THE SUCCESSIVITY RELATION IN COMPUTABLE LINEAR ORDERINGS.
Journal of Mathematical Logic,
Vol. 10,
Issue. 01n02,
p.
83.
Spreen, Dieter
2010.
Programs, Proofs, Processes.
Vol. 6158,
Issue. ,
p.
386.
Kach, Asher M.
and
Montalbán, Antonio
2011.
Cuts of Linear Orders.
Order,
Vol. 28,
Issue. 3,
p.
593.
Frolov, A.
Kalimullin, I.
Harizanov, V.
Kudinov, O.
and
Miller, R.
2012.
Spectra of highn and non-lown degrees.
Journal of Logic and Computation,
Vol. 22,
Issue. 4,
p.
755.
Frolov, A. N.
2013.
A note on Δ 2 0 -Spectra of linear orderings and degree spectra of the successor relation.
Russian Mathematics,
Vol. 57,
Issue. 11,
p.
65.
Greenberg, Noam
and
Knight, Julia F.
2013.
Effective Mathematics of the Uncountable.
p.
50.
2013.
Effective Mathematics of the Uncountable.
p.
1.
Kalimullin, Iskander
Khoussainov, Bakhadyr
and
Melnikov, Alexander
2013.
Limitwise monotonic sequences and degree spectra of structures.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 9,
p.
3275.
Fokina, Ekaterina B.
Harizanov, Valentina
and
Melnikov, Alexander
2014.
Turing's Legacy.
p.
124.
Jura, Matthew
Levin, Oscar
and
Markkanen, Tyler
2016.
A-computable graphs.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 3,
p.
235.
Hirschfeldt, Denis R.
2017.
Computability and Complexity.
Vol. 10010,
Issue. ,
p.
22.
Bazhenov, N. A.
Frolov, A. N.
Kalimullin, I. Sh.
and
Melnikov, A. G.
2017.
Computability of Distributive Lattices.
Siberian Mathematical Journal,
Vol. 58,
Issue. 6,
p.
959.
Miller, Russell
and
Ocasio González, Victor
2019.
Degree spectra of real closed fields.
Archive for Mathematical Logic,
Vol. 58,
Issue. 3-4,
p.
387.
Zubkov, M. V.
and
Frolov, A. N.
2020.
Spectral Universality of Linear Orders with One Binary Relation.
Siberian Mathematical Journal,
Vol. 61,
Issue. 3,
p.
463.
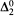 -spectrum of a linear order
-spectrum of a linear order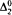 degree, but not 0. Since our argument requires the technique of permitting below a
degree, but not 0. Since our argument requires the technique of permitting below a 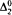 set, we include a detailed explantion of the mechanics and intuition behind this type of permitting.
set, we include a detailed explantion of the mechanics and intuition behind this type of permitting.

